钢玄武岩纤维复合筋混凝土梁受剪承载力试验研究

范旭红，倪林，秦卫红，解鹏，张思博

(1. 江苏大学 土木工程与力学学院，江苏 镇江212013；2. 东南大学 混凝土及预应力混凝土结构教育部重点实验室；国家预应力工程技术研究中心，南京211189)

纤维增强复合材料(fiber reinforced polymer，简称FRP)由于拥有高含量的纤维，使得其抗拉强度相比钢筋具有一定的优势，故近年来关于FRP材料在混凝土结构中的应用获得了学者们的广泛关注。

徐玉野等[1]探究了碳纤维复合材料的加入对混凝土抗震性能的提升效果，卢亦焱等[2]对纤维的加固效果进行了深入研究，吴涛等[3]围绕纤维掺量、纵筋类型、配筋率及纵筋直径等参数对混凝土梁的承载能力、挠度发展、抗裂性能展开了完整、深入的分析，牛建刚等[4]研究了不同纤维掺入量情况下混凝土梁受弯承载力的变化规律。FRP筋混凝土梁受剪方面，Lignola等[5]推导了FRP箍筋梁受剪承载力计算公式，Issa等[6]对不同配箍率的BFRP筋混凝土梁试件进行受剪试验，Refai等[7]深入研究了FRP纵筋轴向刚度对抗剪强度的影响，Alam等[8]探究了FRP混凝土梁尺寸对承载力的影响，张智梅等[9]研究了FRP箍筋梁的受剪承载力，刘宗全等[10]对各国规范中FRP筋混凝土梁斜截面承载力计算公式的可靠性进行了全面的评价。由上述对FRP和混凝土混合材料性能以及FRP梁受弯、受剪的研究可知，以FRP筋替代钢筋作为纵筋虽然可提高梁受弯承载力，但FRP筋弹性模量较低，没有明显屈服点，所以受弯破坏时容易发生脆性破坏，没有明显预兆，正常使用状态下刚度低、裂缝宽度大。并且，FRP筋混凝土梁的受剪承载力比钢筋混凝土梁低。因此，如何在保留FRP强度优势的同时改善其弹性模量低的缺点，并提高构件的刚度、延性和受剪承载力成为推广其应用的关键问题。Bakis等[11]使用AFRP纤维布包裹钢筋制备混杂筋材，吴刚等[12]将钢筋与纤维增强复合材料进行复合，得到新型筋材“钢玄武岩纤维复合筋”，郑百林等[13]则选择使用GFRP材料包覆钢筋，制作了外包玻璃纤维的钢-连续纤维复合筋(steel-basalt fiber composite bar (SFCB)；罗云标等[14]则通过OpenSees软件模拟探究了SFCB混凝土结构在反复荷载下的受力性能。

上述研究表明，SFCB具有明显的二次刚度、且屈服后残余变形较小。尽管SFCB筋弹性模量与抗剪强度高于FRP筋，但是其弹性模量和筋材抗剪强度仍然低于钢筋。因此，SFCB筋材在梁内起到的销栓作用要弱于钢筋。由于销栓作用计算较复杂，现有规范中钢筋混凝土梁受剪承载力公式未单独列出销栓作用贡献，而是将其贡献以及裂缝间骨料咬合作用一起并入到混凝土对受剪承载力的贡献中。如果完全按照钢筋混凝土梁受剪公式计算SFCB混凝土梁，会带来安全隐患。基于梁配筋设计时所遵循的“强剪弱弯”原则，梁的受剪性能应受到重点关注。笔者依据SFCB混凝土梁与钢筋混凝土梁受剪试验结果，研究适用于SFCB的受剪承载力公式，为后续SFCB相关研究提供参考。

1 试验概况

1.1 试件设计

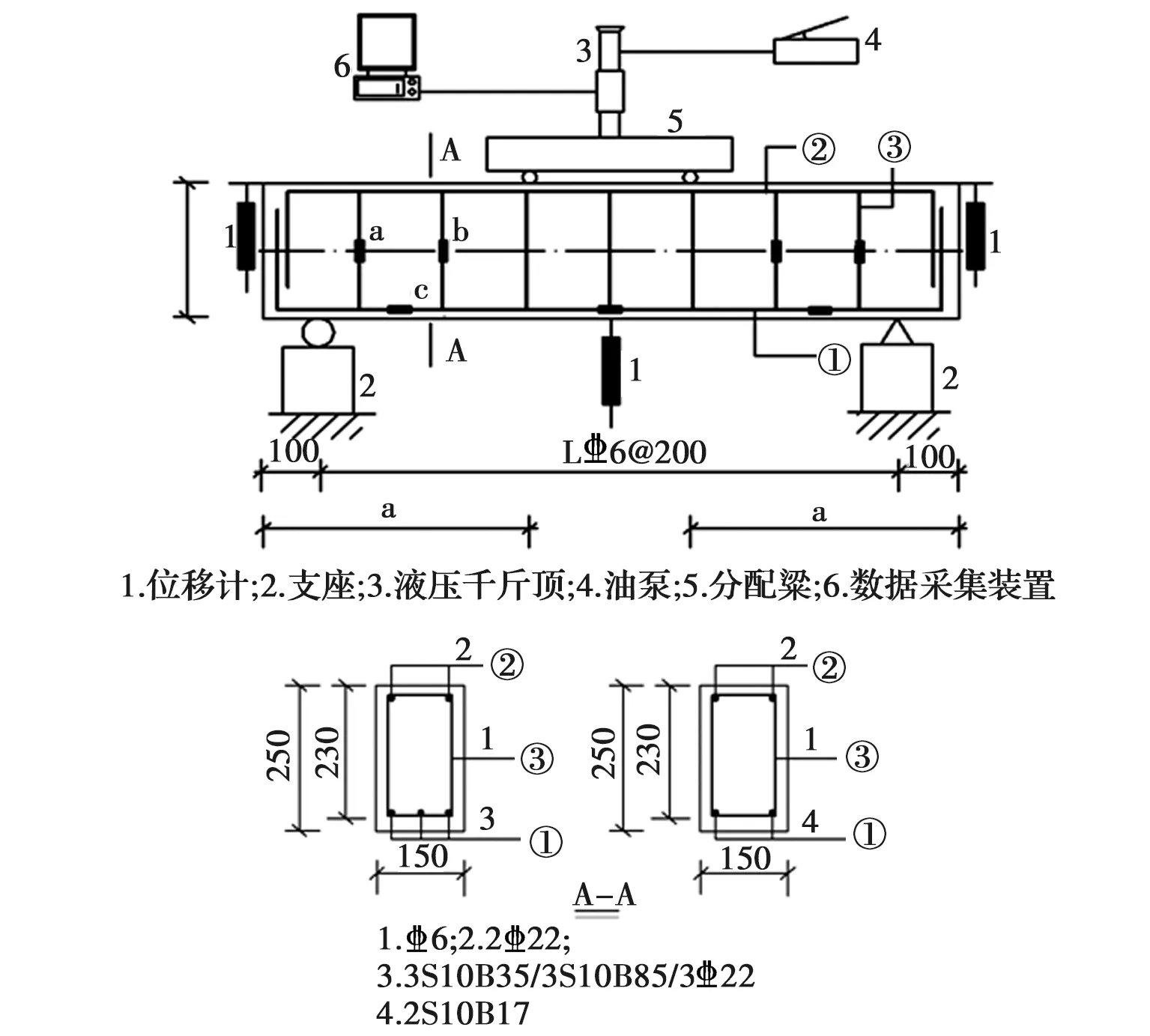
图1 试件详图及测试方案Fig.1 Detail of the specimens and the

表1 梁试验参数Table 1 Test parameters of the beams

1.2 材料性能

试验预留3块立方体混凝土标准试块，养护后进行力学试验。试验所用筋材、混凝土具体力学性能参数见表2～表4。

表2 SFCB筋主要力学性能Table 2 Mechanical performance index of SFCB bars

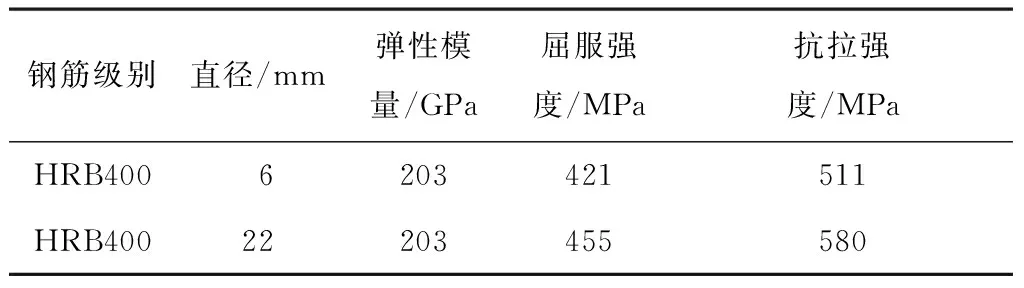
表3 钢筋主要力学性能Table 3 Mechanical performance index of steel bars

表4 混凝土主要力学性能Table 4 Mechanical performance index of the concrete

1.3 加载方案

试验采用四点加载方式施加荷载(如图1所示)。荷载由千斤顶提供，通过力传感器控制。力传感器和应变片均与泰斯特静态应变测试仪相连。试验前先进行15 kN的预加载，然后按照每级5 kN分级加载，在接近开裂荷载及极限荷载计算值时适当放慢加载步。每级荷载加载完等待5 min。试验结果见表5。

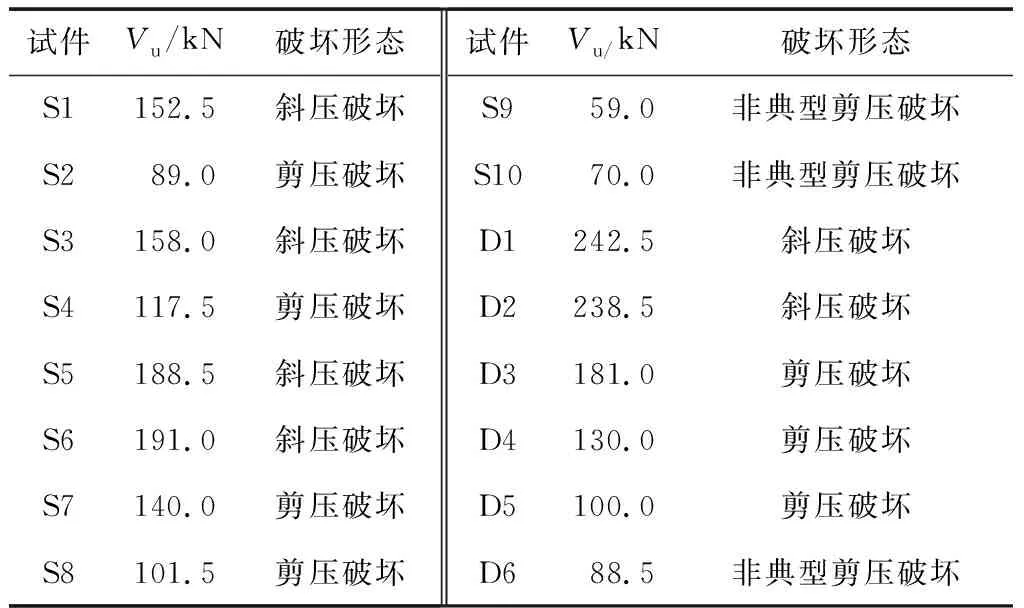
表5 试验结果Table 5 Experimental results

2 试验现象

SFCB混凝土梁的破坏呈现出不同的剪切破坏形态(列于表5)，主要包括斜压破坏，剪压破坏与非典型剪压破坏3种，破坏特征类似于钢筋混凝土梁。典型破坏形态试验照片如图2所示。由于梁所配箍筋均为适中配箍率，所以，影响试件破坏形态的主要因素为剪跨比。

2.1 斜压破坏(以梁S6为例)

斜压破坏大多发生于小剪跨比试件中，试验中小剪跨比为λ≤1。以图2(a)所示的试件梁S6为例，裂纹发展初期表现为梁跨中纯弯段的细小垂直裂缝。随着加载的持续，梁腹弯剪段开始出现多条斜裂缝，斜裂缝大致呈现平行状态，将梁腹分割成若干个有角度的斜向短柱，使得该处混凝土逐渐丧失承载能力；梁腹部主压应力随着荷载提高不断增大，使得斜裂缝逐渐趋于密集。最后，过大的应力导致腹部混凝土发生破碎，试件梁破坏，同时混凝土保护层出现剥落现象。

图2 SFCB试件受剪破坏形态Fig.2 Shear failure modes of the beams with SFCB

2.2 剪压破坏(以梁S4为例)

剪压破坏大多发生于剪跨比适中的试件中，试验中剪跨比适中范围为1<λ<2.5。以图2(b)所示试件S4为例，加载初期，试件梁S4的细小弯曲裂缝首次出现在纯弯段梁底部。随后，剪跨段梁底部也出现细小弯曲裂缝，随着荷载的增加，裂缝开始倾斜。其中1～2条斜裂缝增长速率较快，并迅速发展为临界斜裂缝。临界斜裂缝形成时，梁内与临界斜裂缝相交的箍筋屈服。箍筋屈服之后，临界斜裂缝走向迅速向加载点开展，但发展至一定高度后便不会继续增长，裂缝上部会保持一定高度的混凝土剪压区。直至该处剪压应力超出混凝土承受极限，使得混凝土压碎，梁破坏。

2.3 非典型剪压破坏(以梁S10为例)

试件梁剪跨比较大时，大多会发生非典型剪压破坏，试验中剪跨比λ≥2.5定义为剪跨比较大。图2(c)展示了具备非典型剪压破坏特征的试件梁S10的照片。开始加载后，裂缝最初为跨中纯弯段的细小垂直裂缝，随后，梁剪跨段下部形成垂直裂缝并向腹部倾斜形成斜裂缝。斜裂缝数量少但开展迅速，短时间内便与该处的箍筋相交，其中一条发展为临界斜裂缝。伴随着荷载的增大，与临界斜裂缝相交的箍筋屈服，然后，临界斜裂缝迅速延伸至梁顶部集中加载点，加载点附近的混凝土剪压区面积很小，甚至不能形成剪压区，梁很快破坏。

3 试验结果分析

3.1 箍筋应变

每种破坏模式各选2根SFCB混凝土梁与1根钢筋混凝土梁，根据箍筋(与临界斜裂缝相交的应变较大的箍筋)应变片采集数据，绘制其荷载与箍筋应变的关系曲线，如图3所示。

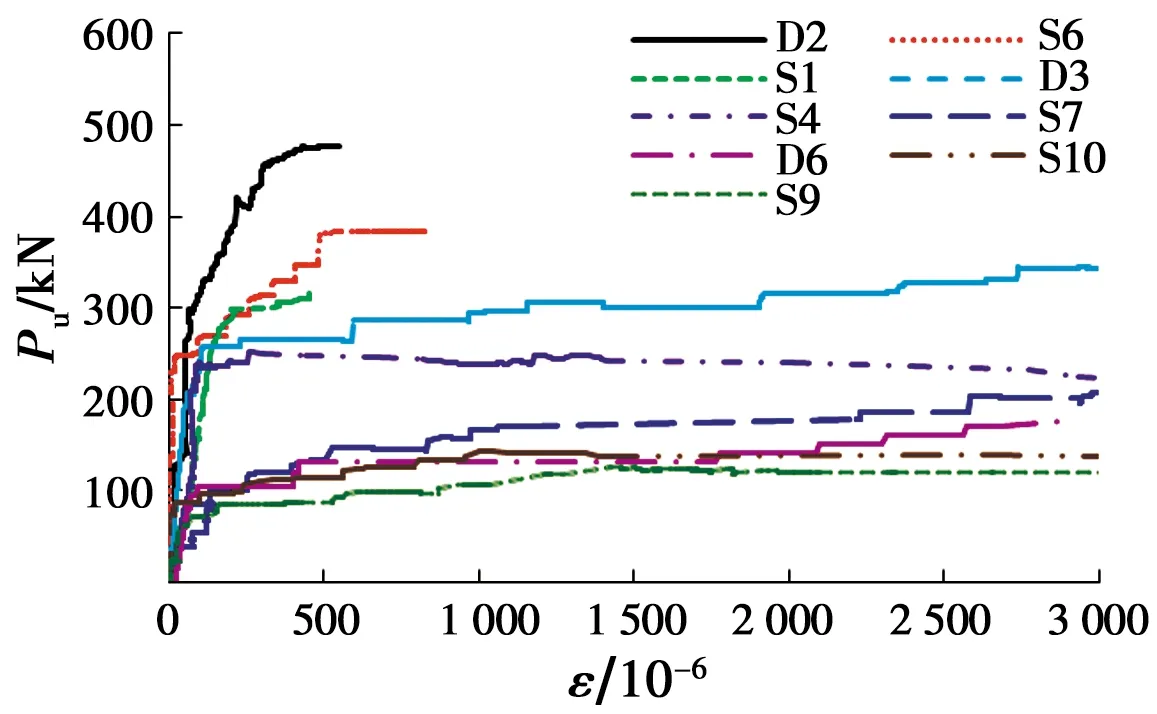
图3 梁荷载-箍筋应变关系Fig.3 Load versus stirrup strain of

由图3可知，梁S1、S6、D2(呈现斜压破坏)箍筋初始应变增长缓慢，达到破坏荷载后箍筋应变增长速率急剧增加，但是梁破坏时箍筋尚未屈服。这是因为斜压破坏模式下，混凝土承载贡献大，箍筋未承受较大的拉力，而当接近破坏荷载后，梁截面发生应力重分布，主要承载部位由混凝土转向箍筋，使得箍筋突然承受过大的拉力，因此，应变迅速增长。但由于混凝土已经承受了大部分荷载，梁破坏前的剩余荷载不足以使箍筋的总应变达到其屈服应变。

梁S4、S7、D3(呈现剪压破坏)箍筋应变在临界斜裂缝形成前增长缓慢。这是因为临界斜裂缝形成前，相比于斜压破坏，箍筋虽承担了更大的应力，但大部分的荷载依旧由剪压区未开裂的混凝土承担。直至临界斜裂缝形成，截面发生应力重分布，梁内与临界斜裂缝相交的箍筋开始工作，应变迅速增长，直至箍筋屈服。

梁S9、S10、D6(呈现非典型剪压破坏)开裂后箍筋应变一直保持较大的增长速率，并迅速达到屈服应变。这是因为，非典型剪压破坏模式下，梁开裂后迅速形成临界斜裂缝。箍筋承担荷载比例很大，因而箍筋应变始终保持着持续增长的状态。临界斜裂缝形成后，箍筋很快屈服，试验梁宣告破坏，破坏荷载与开裂荷载较为相近。

3.2 纵筋筋材影响承载分析

图4为相同纵筋配筋面积情况下不同剪跨比时梁的受剪承载力与纵筋筋材种类的关系图。

图4 梁受剪承载力-纵筋筋材关系Fig.4 Shear capacity versus types of longitudinal

由图4可知，SFCB混凝土梁受剪承载力整体低于钢筋混凝土梁，SFCB筋材横向剪切强度低于钢筋，作为纵筋受剪时发挥的销栓力小于钢筋。由表2、表3可知，SFCB筋材弹性模量小于钢筋，进而导致梁体对斜裂缝的抑制作用较弱，减小了斜裂缝间的咬合力(图7所示的两种梁的斜裂缝宽度图和图12所示的钢筋混凝土梁和SFCB混凝土梁的裂缝分布图可证)，因此，SFCB梁受剪承载力相较于钢筋梁会有所降低。

3.3 纵筋应变

图5为不同剪跨比下试件梁的荷载-纵筋应变曲线，所测纵筋应变均来自与临界斜裂缝相交的剪跨段纵筋。由图5可知，刚开始加载时，纵筋应变均增长缓慢，混凝土开裂后，发生应力重分布，纵筋应变增长速率有所增加。试验中剪跨比较大的梁纵筋应变发展速度较剪跨比小的梁更为迅速。

同时，对比图5中不同纵筋筋材试件梁可以发现，钢筋试件梁剪跨段最终的纵筋应变均较小，未达到屈服应变，剪跨段纵筋均未屈服，而相同剪跨比下的SFCB梁纵筋应变增长速率大于钢筋梁纵筋应变。这是由于SFCB弹性模量小于钢筋，承受荷载后，表现出了更大的应变变形，试验所得应变数据也证实了这一点。所选SFCB梁中，梁S1、S8纵筋最终未屈服，梁S2、S10在箍筋屈服后纵筋也达到屈服。

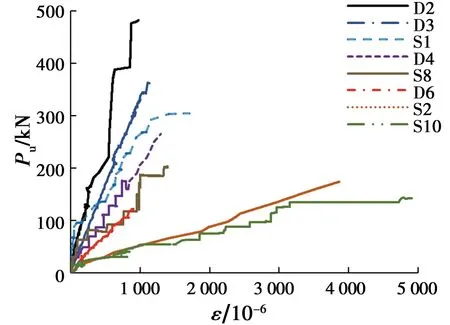
图5 梁荷载-纵筋应变关系Fig.5 Load versus the strain of longitudinal

3.4 剪跨比影响承载分析

图6为不同纵筋筋材与配筋情况下梁的受剪承载力与剪跨比关系曲线。其中，D代表钢筋混凝土梁试验组，S-1、S-2和S-3分别代表纵筋为3S10B85、3S10B35和2S10B17的SFCB混凝土梁试件组。

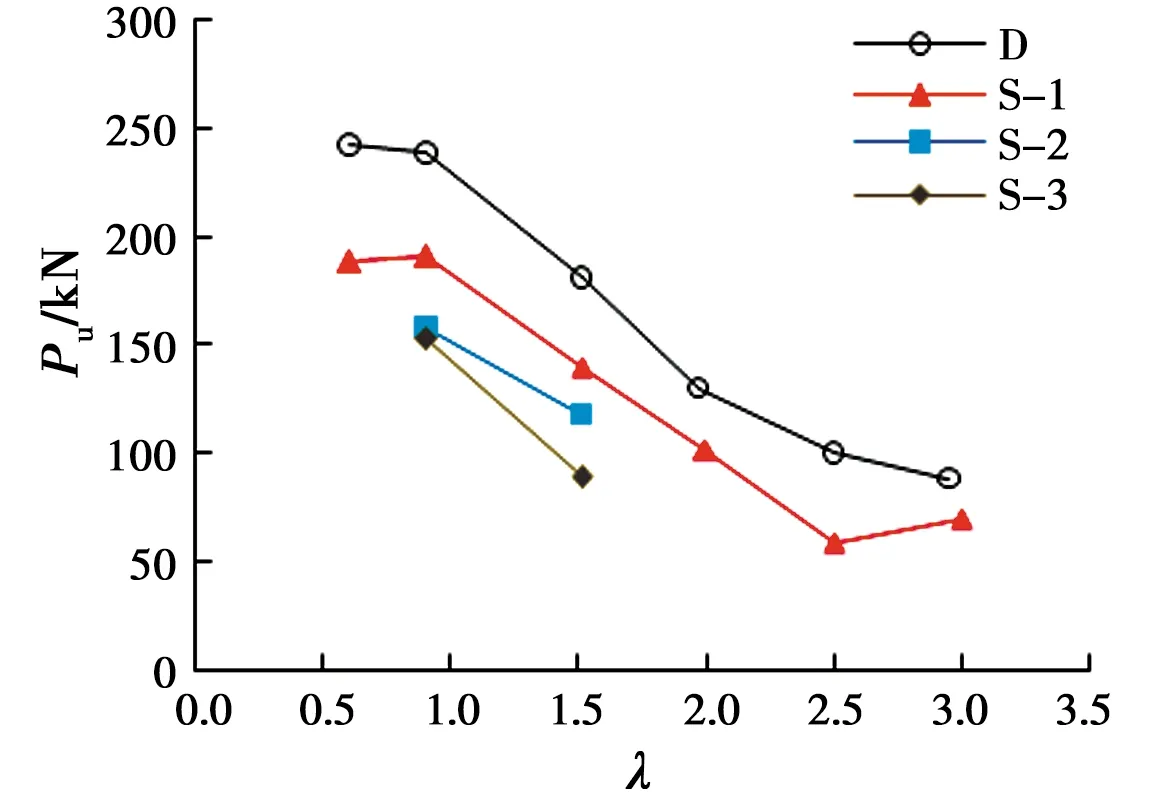
图6 梁的受剪承载力-剪跨比关系Fig.6 Shear capacity versus shear span

由图6可知，试件梁受剪承载力随着剪跨比的增大整体上呈减小趋势。这是因为，随着剪跨比的增大，梁的破坏形态首先由以混凝土受压为主的斜压破坏形态转为由顶部受压区和斜裂缝骨料咬合控制的剪压破坏形态，最后变为以混凝土抗拉强度控制为主的非典型剪压破坏，混凝土对承载力的贡献随之变弱，梁承载力下降。

当1.0≤λ≤2.5时，剪跨比对受剪承载力影响较为明显，承载力随剪跨比增大而减小，而当λ<1.0及λ>2.5时，剪跨比对受剪承载力影响较小。这是因为，剪跨比过大时，拉杆拱机理起主要作用，受剪承载力受剪跨比的影响不大。而剪跨比过小时，梁破坏形态则主要为以腹部混凝土受压控制为主的斜压破坏，此时对承载力贡献较大的是混凝土强度，剪跨比对受剪承载力的影响也不大。故剪跨比过大或者过小时，承载力受剪跨比的影响较小。

从图6还可以看出，SFCB筋混凝土梁的纵筋配筋率越大，受剪承载力越高(S-1>S-2>S-3)。同时还可得到与图4相同的结论：SFCB筋混凝土梁的受剪承载力比钢筋混凝土梁低。

3.5 斜裂缝宽度规律

图7为试件S9、S10、D5、D6的荷载-最大斜裂缝宽度曲线。图中，各试件梁分别在a、b、c、d点箍筋屈服。

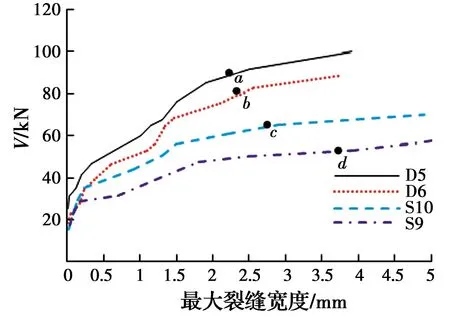
图7 梁剪力-最大斜裂缝宽度关系Fig.7 Shear forces versus maximum crack

由图7可知，试件梁刚开裂时，斜裂缝增长均较缓慢。随着施加荷载的增大，尤其是箍筋屈服后，斜裂缝宽度增长速度加快。SFCB试件梁裂缝整体比钢筋试件梁裂缝发展迅速，产生的裂缝较钢筋试件梁更为宽大。由此可见，SFCB作为受拉纵筋时，对混凝土梁裂缝宽度的约束力不及钢筋。这是因为，相对钢筋，SFCB筋材弹性模量小，作为纵筋时，对斜裂缝开展宽度的抑制作用较弱。

4 SFCB混凝土梁受剪承载力计算方法

4.1 桁架拱模型

试件梁受剪时，梁内纵筋、箍筋以及混凝土部分互相约束与平衡，构成了完整的受剪承载体系，因此，建立能够全面反映承载系统中各部分工作方式的受剪模型，是分析梁受剪承载力的前提。学者们通过理论推导与试验验证，提出多种可用于分析梁受剪过程的模型。其中，桁架拱模型为Ichinose[15]结合欧洲与加拿大规范，建立起的较为完善的混凝土梁受剪承载模型，笔者基于该模型探究试件梁各部分承载工作方式，并推导SFCB混凝土梁的受剪承载力公式。

图8为试件梁桁架拱模型示意图，图中Vc为上部混凝土所受剪力，Vsb为箍筋拉力，Vd为纵筋销栓力，Vu为支座处荷载产生的剪力。为简化计算，假设所有斜裂缝倾角均为φ。梁受剪时，上部纵筋与上部受压混凝土共同组成受压上弦杆，下部纵筋成为受拉下弦杆，梁腹部混凝土与箍筋分别成为受压与受拉腹杆。集中点加载时，腹部混凝土基本呈拱状，将荷载由加载点传递至支座。

图8 桁架拱模型示意图Fig.8 Schematic diagram of truss-arch

4.2 模型受力分析

4.2.1 桁架拉杆 图9为桁架拉杆隔离体，AB为桁架模型斜裂缝破坏面。桁架拉杆合力主要来自于箍筋产生的拉力和纵筋的销栓力。根据图中平衡关系可得

(1)

式中：T为拉杆合力；Asv为截面配箍面积；ρsv为配箍率；fyv为箍筋抗拉强度；D为上下部纵筋距离；s为箍筋间距；b为试件梁截面宽度；Vd为纵筋销栓力。

图9 拉杆部分示意图Fig.9 Schematic diagram of the tensile

4.2.2 桁架压杆 图10为桁架压杆隔离体，CD为混凝土受压截面。桁架压杆合力主要来自于混凝土受压后产生的作用力。根据图中平衡关系，得到式(2)。

C=σcbh0cosφsinφ

(2)

图10 混凝土斜压杆部分示意图Fig.10 Schematic diagram of the concrete compression

式中：C为压杆合力；σc为混凝土压应力；h0为梁的有效高度。

平衡桁架拉压杆合力，即T=C，可得

ρsvfyvDbcotφ+Vd=σcbh0cosφsinφ

(3)

(4)

4.2.3 混凝土拱体 如果箍筋屈服的同时，混凝土便失去承载能力，则梁体极易发生脆性破坏，破坏无明显预兆。为规避这种情况，通常要求箍筋屈服即桁架受拉腹杆达到极限承载后混凝土依旧具有剩余承载强度，即式(5)，以保证梁体具有一定的延性。

σk=vfc-σc

(5)

式中：σk、fc分别为混凝土剩余承载强度和抗压强度；v为混凝土软化系数。由于混凝土受剪后产生软化现象，受压强度降低，故需乘以软化系数。v采用美国规范[16]中规定的数值，即v=0.6。

桁架承载达到极限后，混凝土部分会形成拱体状继续承载，因此，σk亦可视作混凝土拱体的强度。

图11为梁构件混凝土拱体示意图。图中，Xc为混凝土拱剪压区高度。由图11平衡关系与几何关系可得

(6)

(7)

式中：Vk为混凝土拱剪力；a为梁剪跨长度；α为混凝土拱倾角。

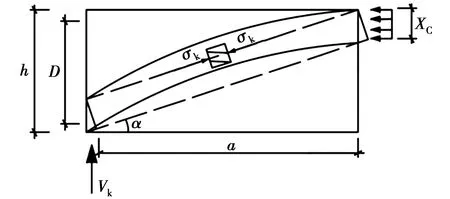
图11 混凝土拱体示意图Fig.11 Schematic diagram of the concrete

由于SFCB筋比钢筋弹性模量低，对梁裂缝开展的约束能力低，从而使得混凝土拱体顶部产生不同的剪压区高度。试验中，SFCB梁斜裂缝和弯曲裂缝的平均延伸长度比其他参数相同的钢筋混凝土梁的长度长。因此，其剪压区高度较小(见图12两种纵筋梁剪压区高度的对比)。经过对试件剪压区高度实测数据的统计，SFCB梁与钢筋梁剪压区高度xc的大小分别约为0.28h0与0.35h0。

图12 SFCB试件梁与钢筋试件梁剪压区高度对比Fig.12 The compression depth of the beams with

4.3 纵筋销栓力

关于销栓力Vd，规范[17]和有关文献尚未有明确的计算公式，笔者结合试验数据分析销栓力的计算方法。

当混凝土梁受剪时，其受拉纵筋所起的作用类似于螺栓受力。但是由于纵筋较细长，一般不会发生纯剪切破坏(图13(b)为文献[18]中的FRP筋纯剪切破坏试验照片)，筋材无法完全发挥抗剪强度，而是发生介于弯曲和剪切之间的破坏状态(图13(a)、(c))。

假定筋材发生理想的纯剪破坏(图13(d))，则其销栓力可按式(8)计算。

Vd1=Asfv

(8)

式中：fv为筋材的抗剪强度。关于fv的取值，由塑性力学的强度理论可知，钢筋的抗剪强度约为抗拉强度的0.58倍。FRP筋材抗剪强度约为抗拉强度的0.10倍[18]。SFCB筋材由钢筋与FRP筋复合而成，按复合面积比例，SFCB筋材抗剪强度可按式(9)计算。

(9)

式中：Sf、Sb分别代表SFCB横截面上FRP、钢筋的面积，ftf、ftb分别表示FRP、钢筋的抗拉强度。

图13 纵筋在梁中实际受力与理想剪切时的破坏形态Fig.13 Shear failure modes of the longitudinal

若假定纵筋的销栓力等于纵筋受纯剪切时的破坏力，则根据所配置的受拉纵筋情况，由式(8)算得各根梁的销栓力Vd1如表6所示。从表6可见，该计算方法过高地估计了纵筋的销栓作用。

表6 不同纵筋纯弯、纯剪销栓力计算结果Table 6 The dowel action of the different longitudinal bar in bending and shearing

如图13(a)所示，梁在发生斜截面受剪破坏时，纵筋不可避免存在弯曲变形。由于箍筋的约束作用，假定纵筋发生纯弯曲的两个弯曲点位于与箍筋相交处(如图14所示的A、B两点)，忽略其他部位的弯曲变形，根据虚功原理，外力虚功(剪力V在虚位移Δ上产生的虚功)等于内力虚功(筋材本身的弯曲塑性铰在转角上所作的虚功)，因此有

2Mθ=VΔ

(10)

又因为θ≈tanθ=Δ/s，故可得到

(11)

式中：Vd2为纵筋本身的弯曲变形提供的销栓力；n为纵筋数量；s为箍筋间距；W为单根纵筋截面抵抗矩，取πd3/32；fy为纵筋屈服强度。

图14 纵筋弯曲部分示意图Fig.14 Schematic diagram of the bending

由式(11)可以计算得到只考虑纵筋弯曲变形贡献的销栓力，将计算结果也列于表6。由表6可见，由此方法计算的销栓力结果又过于保守，低估了纵筋的销栓力。因此，纵筋实际受剪时的销栓力应假定为抗剪强度提供销栓力的部分贡献与筋材弯曲变形提供的销栓力之和，即

Vd=kVd1+Vd2

(12)

式中：k为纵筋销栓力折减系数。

4.4 受剪承载力计算公式

由上述分析可知，梁剪力由桁架杆与混凝土拱共同承担，即

Vcal=T+Vk

(13)

Vcal=ρsvfyvDbcotφ+Vd+σkbxctanα

(14)

其中：

(15)

(16)

式中：Vdt为纵筋受剪部分实际贡献销栓力。

4.5 销栓折减系数k的取值

基于表5试验数据与式(14)，反算得到所有试件梁的受剪部分实际贡献销栓力Vdt，并根据其与筋材受剪承载力Asfv的关系对系数k进行回归求解。

图15为各试件梁Vd1与Asfv构成的散点图，图中线段斜率即表示纵筋销栓力与混凝土梁筋材本身受剪承载力的关系，即销栓折减系数k。由图15可知，混凝土梁的k值取为0.15较为合适。

图15 SFCB梁和钢筋梁k值回归结果Fig.15 The result of k values of SFCB beams and reinforced concrete beams from regressive

4.6 斜裂缝倾角φ的取值

如前所述，φ可视为试件梁斜裂缝平均倾角。由式(1)可知，斜裂缝倾角越大，与斜裂缝相交的箍筋数量越少，箍筋拉力总和越小，故斜裂缝角度φ对梁的斜截面受剪承载力影响显著。

图16为SFCB试件梁S8与钢筋试件梁D4(所述两根梁仅纵筋筋材不同)全梁裂缝对比图，图中蓝色虚线为两根梁的斜裂缝走向。由图16可以看出，SFCB试件梁斜裂缝与构件纵轴的夹角略大于钢筋混凝土梁。造成这种现象的原因是，SFCB筋弹性模量低于钢筋，在相同的荷载增量下，它对斜裂缝开展的约束小于纵向钢筋的约束作用，影响了混凝土主拉应力的方向，进而影响了斜裂缝的走向。

图16 SFCB试件梁与钢筋试件梁斜裂缝对比Fig.16 Diagonal cracks of the beams with SFCB and steel

变角桁架拱模型中只限制了受剪梁斜裂缝倾角的上限值为45°，并未给出斜裂缝倾角具体的求解方法[19]。根据文献[20]，纵筋销栓力约束了斜裂缝的开展，两者之间的关系为

(17)

式中：Vd为纵筋销栓力；ES为纵筋弹性模量；σS为纵筋应力；εS为纵筋应变；AS为纵筋配筋面积。

基于试验测得的纵筋应变数据以及计算得到的纵筋销栓力，在变角桁架拱理论限制的倾角范围内，计算得到SFCB与钢筋梁斜裂缝倾角均值分别为45°与40°。表7为所有试件梁斜裂缝倾角量测统计结果，由表7可知，式(17)计算所得倾角值与试验中梁的倾角大致相符。

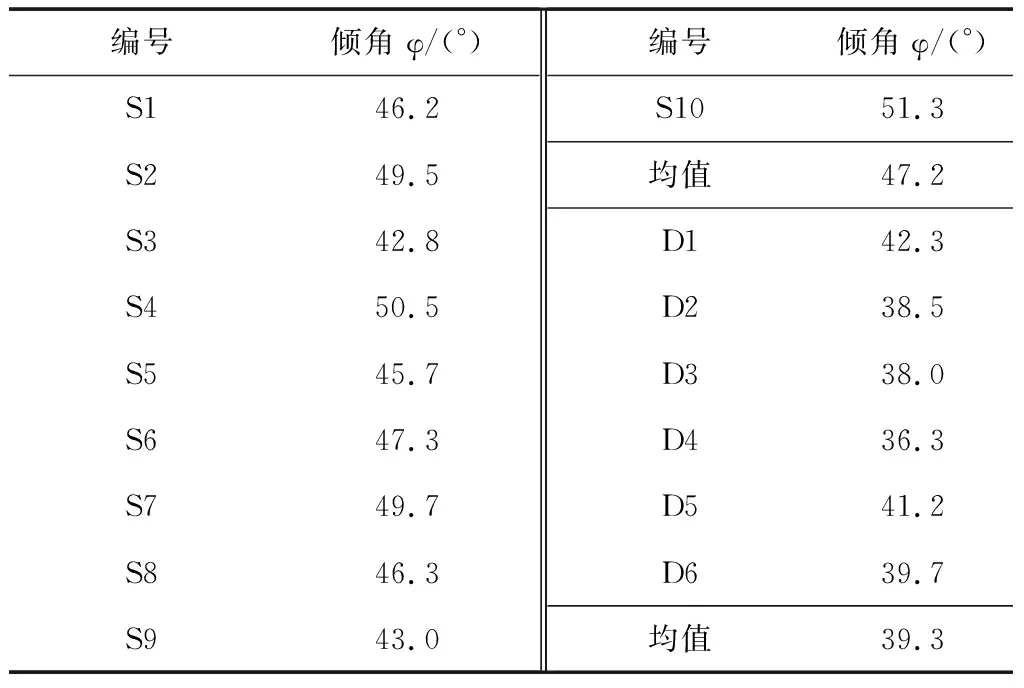
表7 斜裂缝倾角量测统计结果Table 7 Measurement results of the diagonal cracks angles

4.7 公式验证

将式(14)计算结果与试验值同列于表8。由表8可知，当梁满足1.0<λ<2.5时，式(14)的计算结果在整体略小于试验结果的基础上吻合较好，且基本反映了剪跨比对承载力的影响。因为此时梁多发生剪压破坏，传力机理明确，计算精度高。而当λ≤1.0时，式(14)计算结果则偏于保守，因为式(14)是在正常的剪压破坏基础上进行推导的，而剪跨比较小时，试件梁多发生斜压破坏，承载力高于正常的剪压破坏。而当λ≥2.5时，试件梁多发生非典型剪压破坏，受剪承载力低于正常的剪压破坏梁，破坏十分突然，因此，大剪跨比时理论结果比试验值稍大。

由此可见，式(14)用于剪跨比适中的SFCB及钢筋混凝土梁的受剪承载力计算时具备较高的安全性与适用性，可为后续的SFCB混凝土梁研究和应用提供一定的参考依据。

表8 试件梁受剪承载力试验值与计算值对比Table 8 Comparison of shear capacity of beams between experimental values and calculated values

5 结论

基于SFCB筋和钢筋作为纵筋的混凝土梁受剪承载力对比试验，得出以下结论：

1)SFCB混凝土梁受剪承载力整体低于钢筋混凝土梁。

2)配箍率适中的SFCB筋混凝土梁受剪破坏时有3种破坏模式：剪跨比较小(λ≤1.0)时为斜压破坏，剪跨比适中(1.0<λ<2.5)时为剪压破坏，剪跨比较大(λ≥2.5)时为非典型剪压破坏。

3)SFCB混凝土梁受剪承载力随着剪跨比的增大整体呈减小趋势。当λ<1.0和λ>2.5时，剪跨比对受剪承载力影响较小，而当1.0≤λ≤2.5时，剪跨比对受剪承载力的影响则较为明显。

4)SFCB筋混凝土梁受剪承载力随着纵筋配筋率的增大而增大，多数试件梁破坏时，受拉纵筋均未屈服。

5)与钢筋混凝土梁相比，SFCB混凝土梁承受荷载后会产生更宽更长的斜裂缝且裂缝发展速度整体快于钢筋混凝土梁，由此可知，SFCB混凝土梁受剪时所展现的斜截面抗裂性不及钢筋混凝土梁。

6)基于桁架拱模型，推导了混凝土梁受剪承载计算公式，计算公式对剪跨比适中的SFCB混凝土梁受剪承载计算具有较高的安全性与适用性。