渝昆高铁典型连续梁桥地震易损性分析

户东阳

渝昆高铁典型连续梁桥地震易损性分析

户东阳

(中铁二院昆明勘察设计研究院有限责任公司，云南 昆明 650200)

为评估渝昆高铁典型三跨连续梁桥的抗震性能，基于概率地震需求分析方法对该桥进行理论地震易损性分析。选取渝昆高铁沿线实测地震动记录作为地震输入，考虑桥梁参数的不确定性，采用拉丁超立方抽样方法生成桥梁有限元模型样本库。基于增量动力时程分析方法，通过对桥梁样本库进行非线性时程分析，获得了各构件地震响应峰值，通过峰值响应与地震动峰值加速度的线性回归分析建立构件地震需求模型。进一步对比研究安装普通球型钢支座与双曲面球型减隔震支座桥梁的地震易损性曲线。研究结果表明：减隔震支座可有效降低制动墩易损概率，优化墩高不等的非规则桥梁结构的抗震性能。其研究方法与结论可为非规则连续梁桥抗震设计提供参考。

连续梁桥；地震易损性；减隔震支座；渝昆高铁

重庆至昆明高速铁路位于我国西南地区的重庆市、四川省、贵州省和云南省境内，线路自重庆枢纽引出后，沿途经过重庆江津和永川区、四川泸州和宜宾市、贵州毕节市、云南昭通和曲靖市后接入昆明铁路枢纽。线路从四川盆地爬升至云贵高原，沿线地质条件复杂，为跨越这些沟谷深壑、地势复杂地区，线路中广泛采用典型连续梁桥桥型。由于地形原因，使得这些桥梁具有跨度大、桥墩高、相邻桥墩高差大等特征。另一方面，线路区域内断裂构造发育，主要为顺线路走向，少量垂直线路走向。其中许多断裂规模巨大，切割深，发展历史复杂。非规则的桥梁类型和活跃的断裂带，给这类非规则桥梁的抗震设计带来巨大挑战，桥梁建成后的运营安全也受到地震的严重威胁。因此急需对铁路典型三跨连续梁桥的抗震性能进行研究。地震易损性分析法已伴随不断发展的桥梁抗震评估理论成为桥梁抗震性能评估的普适方法[1]。结构地震易损性其本质是地震响应大于本身抗震能力的条件概率问题。目前，地震易损性分析方法可分为3类[2]：理论分析型、历史经验型与专家评判型。由于后2种方法的分析结果极易受到桥梁震害信息详实程度的影响，国内外学者常采用分析型易损性曲线方法评估结构抗震性能。Roy[3]基于传统易损性指标，提出一种基于最大可信度的损伤指标，用于典型钢筋混凝土桥墩的地震易损性分析。Dezfuli等[4]采用地震易损性分析方法研究了具有特殊减隔震装置的高速公路连续梁桥抗震性能。Lee等[5]通过地震易损性分析方法研究了铅芯橡胶支座对钢箱梁连续梁桥抗震性能的影响。在国内，杨恺[6]运用概率地震易损性分析方法对一座V腿连续梁桥在服役期间材料退化后的抗震性能及地震风险进行了研究。吴姗姗等[7]针对我国常见铁路简支梁桥进行了三维地震易损性分析，评估了该类桥梁的抗震性能。马腾[8]对铁路常见三跨简支梁桥的桥墩和支座进行了地震易损性分析及风险分析。王君[9]采用IDA地震时程分析方法，对某高速铁路连续梁桥进行了抗震性能评估。然而，上述研究主要集中于评估常见公路、铁路简支梁桥、公路中小跨径连续梁桥的抗震性能，对于铁路高墩、大跨连续梁桥的地震易损性研究还不充分，此外对于不同类型支座对铁路连续梁桥抗震性能的对比研究也尚少。本文以渝昆高铁某典型三跨连续梁桥(70+128+70) m为研究对象，基于Frame3D建立了该桥有限元模型，考虑桥梁结构及地震动输入的不确定性，建立了桥梁-地震动分析样本库，采用IDA分析方法对样本库进行动力时程分析。基于概率地震需求分析方法，获得了该桥各易损构件损伤程度与地震强度变化曲线，最后，对比分析了2类支座对桥梁抗震能力的影响。

1 地震易损性分析理论

1.1 概率地震需求分析

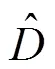
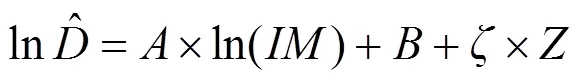
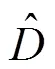
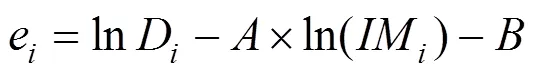
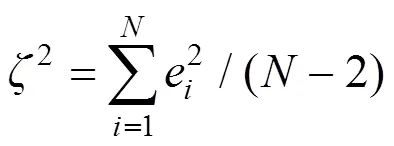
1.2 桥梁构件地震易损性

由上述桥梁地震易损性的基本定义[11]，桥梁构件地震响应超过自身抗震能力的条件概率可表 达为：

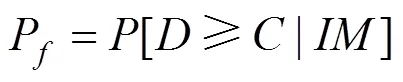
式中：P为超越既定损伤状态的条件概率。当，均满足对数正态分布时；P概率密度函数与，保持一致，基于对数正态累计概率密度函数的定义，桥梁构件易损性函数[11]可写成如下形式：

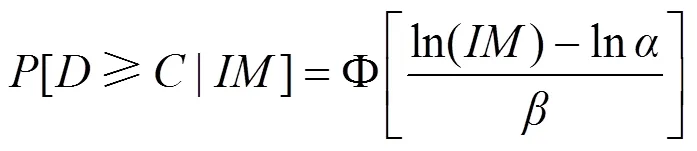
1.3 铁路三跨连续梁桥易损性分析流程

基于上述分析理论，本文给出了渝昆高铁典型三跨连续梁桥地震易损性的分析流程，如图1所示。

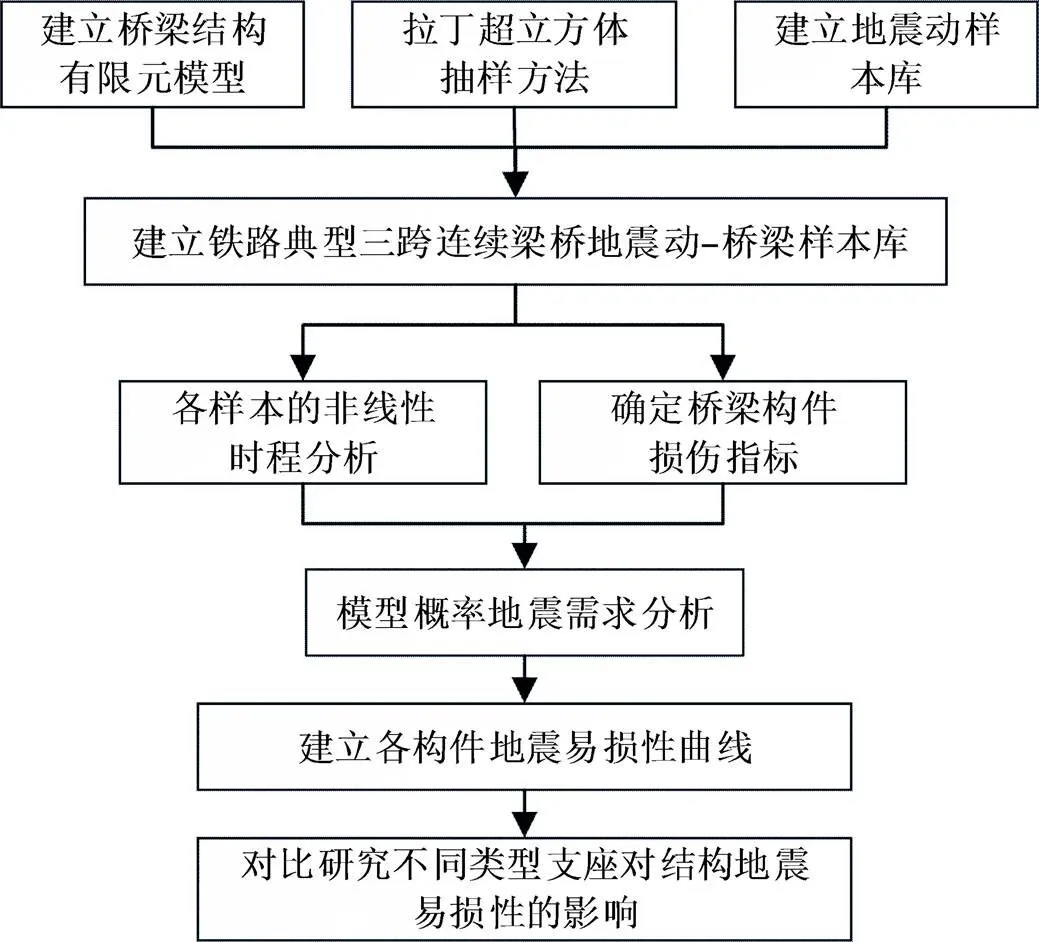
图1 铁路三跨连续梁桥地震易损性分析流程

2 桥梁实例分析

2.1 工程概况

以渝昆高铁八家村2号双线特大桥为例，基于图1的分析流程，讨论了线路中典型三跨连续梁桥的地震易损性。该桥主梁采用变截面连续箱梁形式，桥跨布置为(70+128+70) m，C55混凝土；各桥墩均采用圆端空心截面形式，采用C35混凝土，1号～4号墩墩高为：22，23.5，16和21 m (如图2所示)，其中2号墩为制动墩，桥墩纵向配筋率为1.35%，配箍率为0.84%，纵筋、箍筋型号均为HRB400；本文对比了2类支座条件下桥梁结构地震易损性程度，2种支座类型的具体型号详见表1，对于球型钢支座，纵向活动支座设计水平力取设计竖向承载力的5%，固定支座设计水平力取设计竖向承载力的30%；对于纵向活动和固定的双曲面球型减隔震支座(以下简称减隔震支座)，其设计水平力均为设计竖向承载力的20%。

表1 各桥墩球型钢支座参数汇总

2.2 有限元模型

本文采用专业桥梁抗震软件Frame3D模拟全桥模型。已有研究表明[1, 8]，在地震作用下，桥梁结构主梁一般呈线弹性状态，因此主梁均采用线弹性梁单元模拟，主梁施加结构自重、二期恒载和列车活载。为获得精细化的桥墩损伤结果，本文采用弹塑性纤维单元(Force Beam Column Element)模拟各个桥墩构件，桥墩中无约束和约束混凝土，采用Kent-Scott-Park模型[12]模拟其力学特性，桥墩钢筋的力学行为则遵从Giuffre-Menegotto-Pinto模型[13]。对于支座的模拟，采用与文献[14]一致的方法，用双线性理想弹塑性弹簧单元模拟，由于本文拟研究球型钢支座和双曲面球型减隔震支座对构件地震易损性的影响，因此根据2种支座的具体设计参 数[15](表1)，需分别定义出2种支座的屈服前和屈服后刚度，具体参数定义方法详见文献[1]。采用等效边界单元模拟桩基础，即在桥墩底部采用6个弹簧等效模拟桩土效应，6个弹簧的刚度分别为竖向刚度、顺桥向的抗侧刚度、横桥向的抗侧刚度、绕竖轴的抗扭刚度、顺桥向的抗弯刚度以及横桥向的抗弯刚度[16−17]。在单元划分时，桥墩构件单元网格尺寸较小，划分密，梁单元网格较大，划分粗，在保证分析精度的前提下，以便降低地震动力时程分析的计算时间。桥梁有限元模型示意图如图3所示。

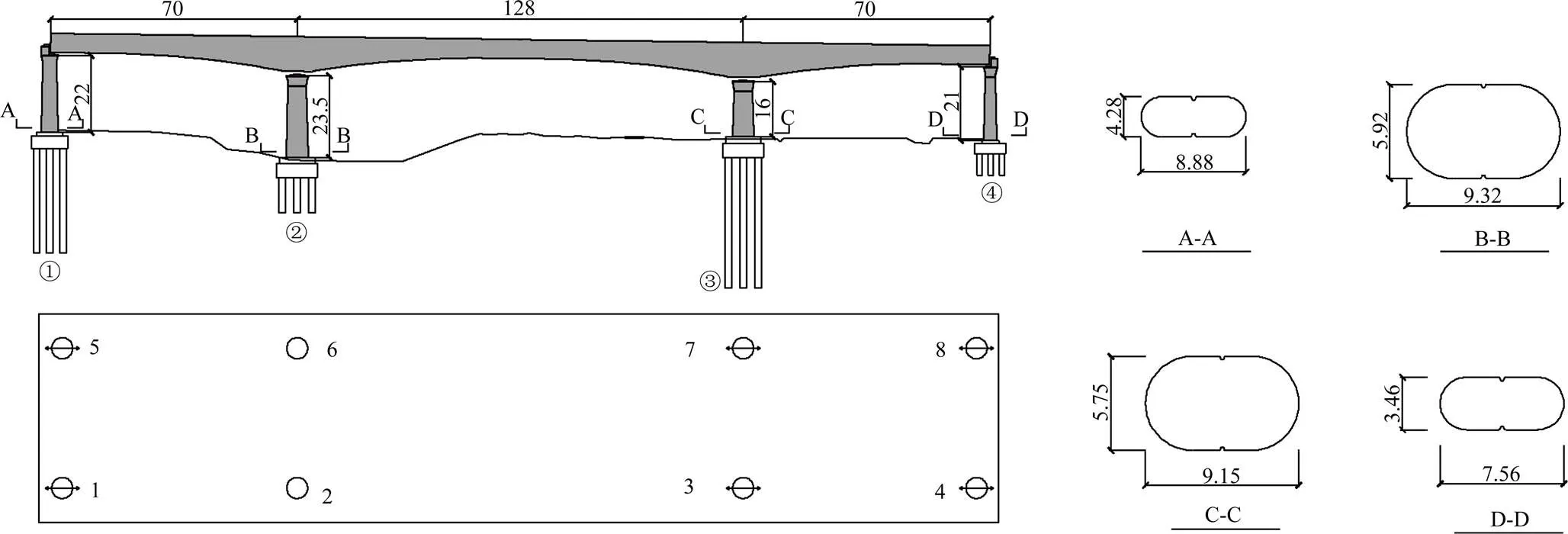
单位：m

图3 有限元模型示意图

2.3 模型参数的不确定性

2.3.1 地震动输入

目前国内外学者常根据峰值型、频谱型及综合型3种强度指标来选取地震动输入[18]。渝昆高铁跨越长江中游地震带、右江地震带和鲜水河～滇东地震带等多个活动地震带，本文在选取地震动时尽可能选用沿线实测地震动数据，以便真实反映渝昆高铁的抗震性能。综合考虑地震波形完好性、地震有效持时、地震动PGA水平、地震频谱特征等因素[18]后，在四川省内20个地震观测台站中选取60条地震加速度作为本文桥梁地震动时程分析的地震激励。表2给出了20个观测台站具体名称及其峰值加速度值，地震加速度波形示意图如图4所示，各地震动的加速度反应谱及其均值谱如图5所示。

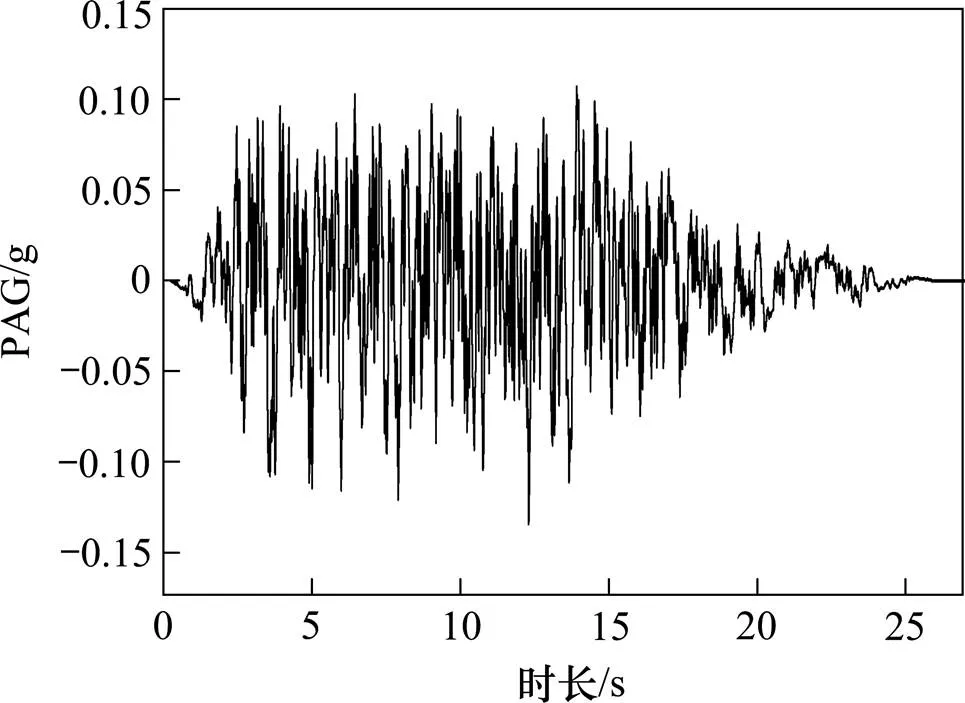
图4 地震加速度时程波形图

2.3.2 桥梁结构参数的不确定性

针对渝昆高速铁路典型三跨连续梁桥，由于桥梁建筑材料选择、施工方法的差异、桥梁所处环境的不同、施工人员众多等因素影响，使得实际桥梁结构具有不确定的材料特性、构件行为特征及作用荷载效应，从而造成桥梁结构自身抗震能力和地震响应均表现出不确定性的特征，因此在建立桥梁结构−地震样布库时，需将这些不确定因素包含进来。针对结构参数不确定性对桥梁抗震性能的影响，Nielson等[19−20]在开展桥梁结构抗震性能研究过程中确定了各类结构参数不确定性的分布类型及特征值，并研究了结构参数不确定性对结构自身抗震性能的影响，明确了影响桥梁结构抗震性能的主要参数。本文借鉴上述研究成果，确定了桥梁模型中不确定性参数及其分布，如表3所示。

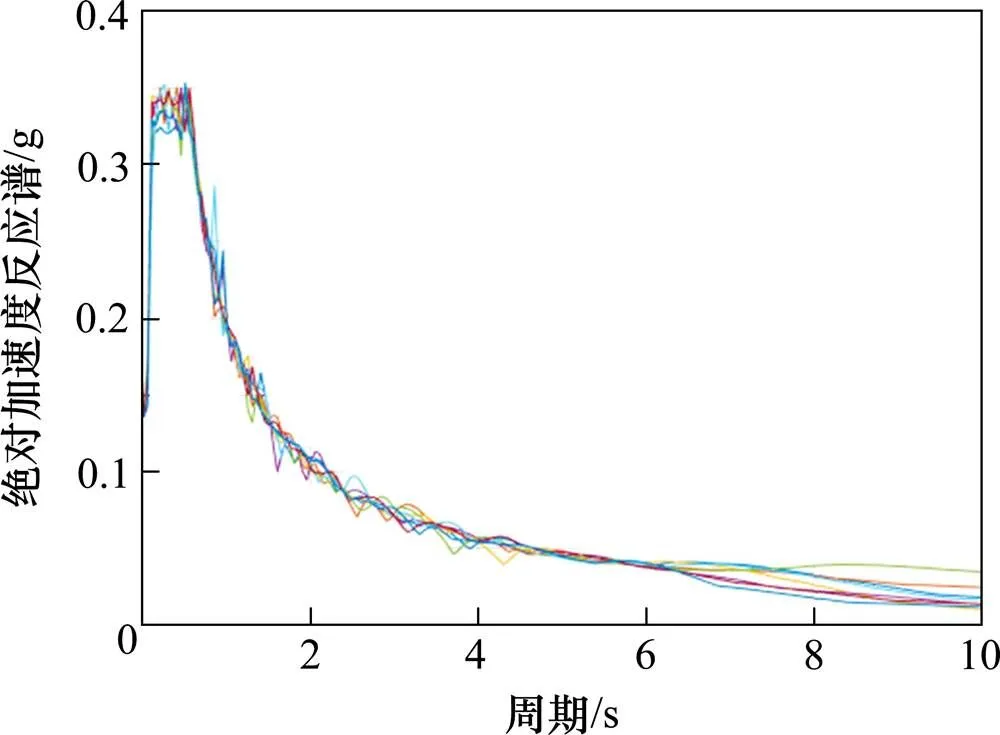
图5 反应频谱特性图(ξ=0.05)

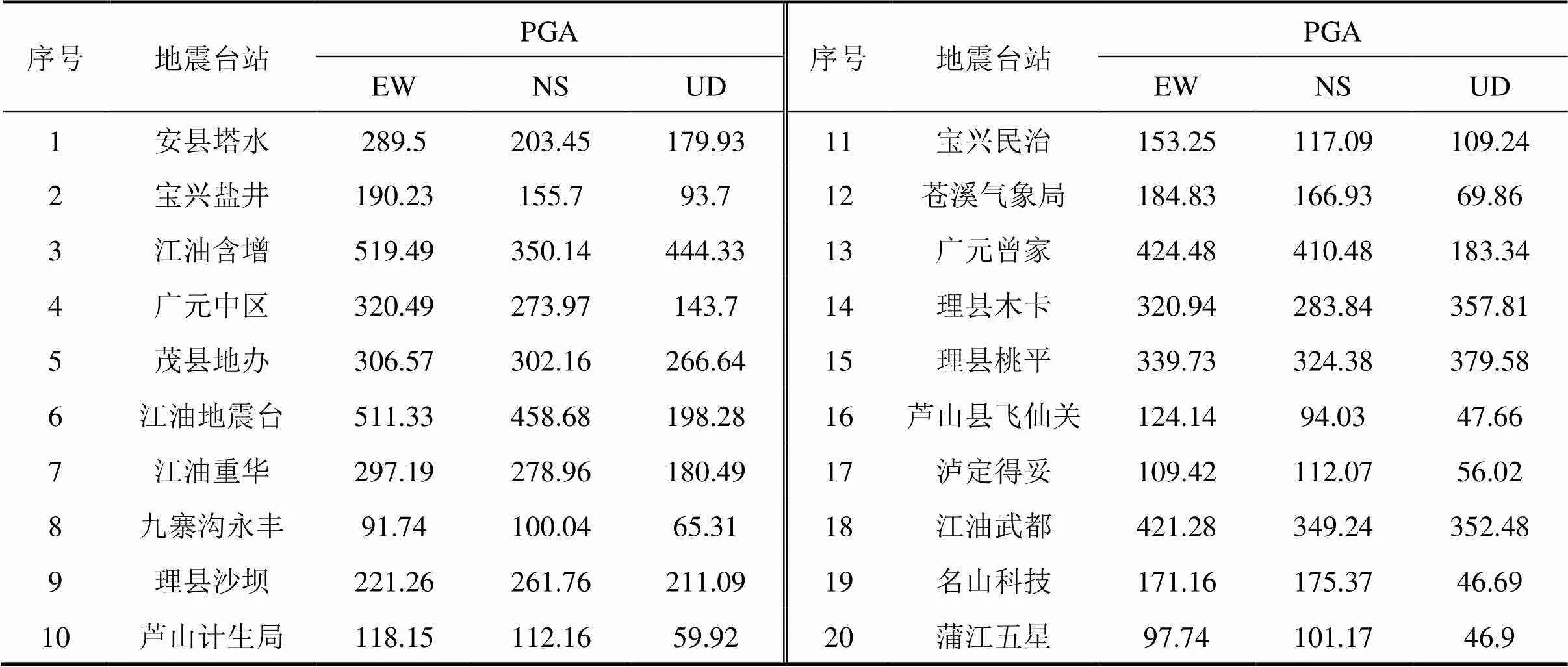
表2 地震观测台站信息

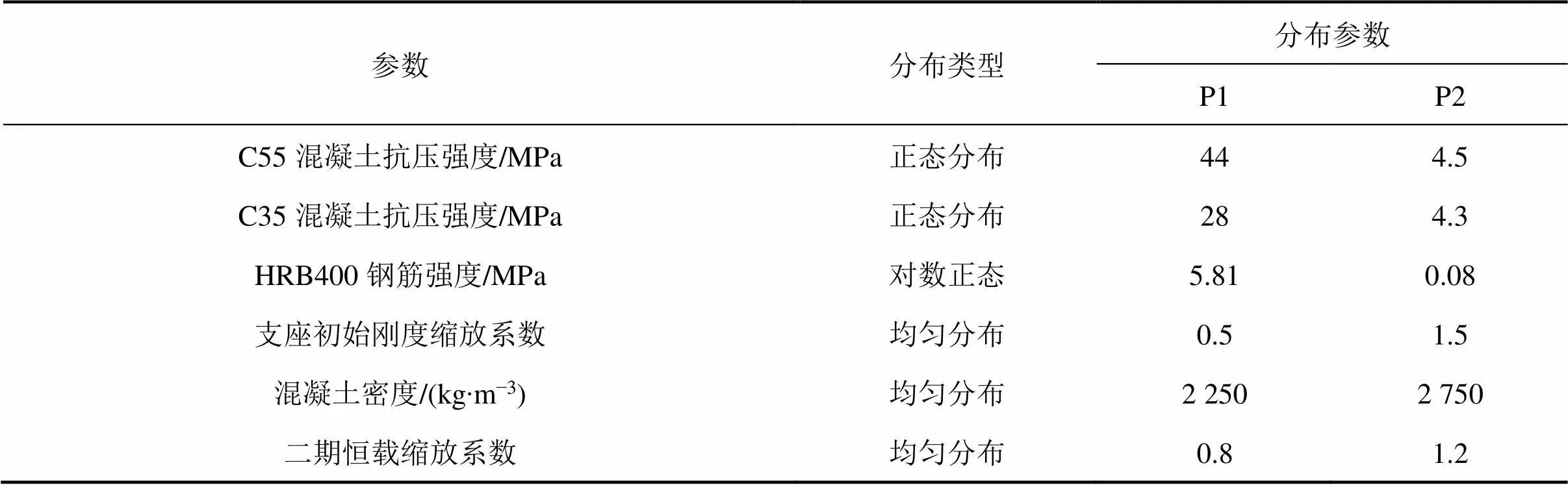
表3 桥梁结构参数分布特征表

2.4 桥梁构件损伤指标

基于文献[3, 5]的研究结果，并考虑本文背景桥梁高墩、大跨的结构特征，选择曲率延性比作为墩柱损伤指标，其计算方法详见文献[21]。由于目前还没有统一可靠的铁路球型钢支座和减隔震支座损伤程度量化阈值指标的规范和标准，本文在制定支座的损伤指标时，参考相关资料[21]后，采用支座位移建立了2种类型支座的损伤阈值。铁路三跨连续梁桥桥墩和支座4个不同损伤状态对应的损伤指标中位值如表4和表5所示。其中，β计算公式中COV在轻微和中等损伤状态下取值0.25，严重和完全破坏状态下取值0.5[1]。

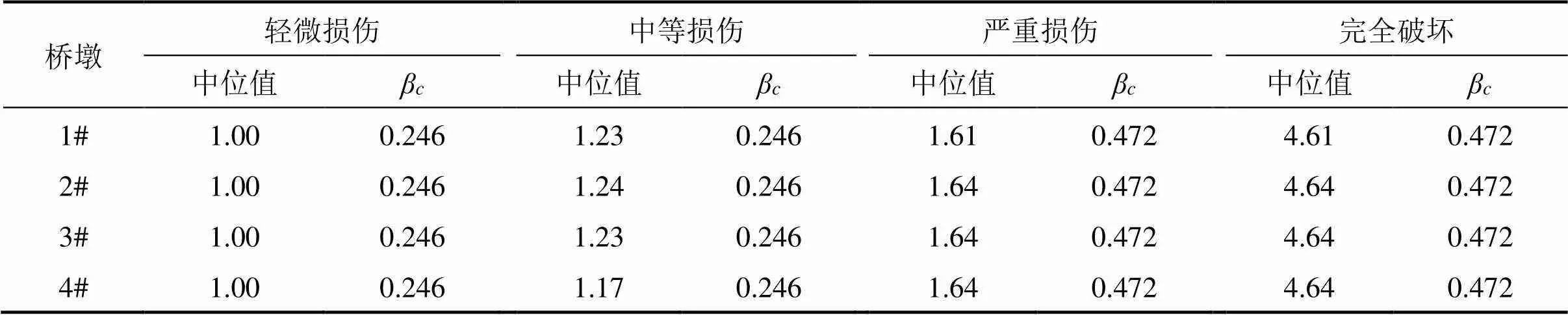
表4 桥墩各损伤指标参数

表5 支座各损伤指标参数

注：LQZ表示球型钢支座；KZQZ表示双曲面球型减隔震支座。

2.5 铁路三跨连续梁桥地震易损性分析

首先建立包含模型参数及地震动不确定性的桥梁有限元模型，确定桥梁各构件损伤指标之后，然后进行基于IDA地震动力时程分析，获得分析结果后便可用式(6)建立各构件地震动强度与损伤程度相关性曲线。图6和图7分别为3.3.1节顺桥向地震动PGA=0～1.0时，2种支座类型条件下各桥墩和支座构件的4种损伤状态对应的地震易损性曲线。由图可知，2种支座类型下，虽然各构件具有相似的易损性曲线，但各构件在不同损伤状态下对应的损伤概率差异显著。

由图6分析表明：

1) 对于安装普通球型钢支座的各桥墩，当PGA为0.3(抗震烈度为8度)时，2号墩(安装固定支座，以下称为制动墩)在轻微损伤状态下破坏概率为30%左右，其他非制动墩(安装活动支座的桥墩，以下称为非制动墩)在轻微损伤状态下的破坏概率均小于10%，而其他3个级别损伤状态(即中等、严重和完全破坏)对应构件的损伤概率均接近0，这反映了该连续梁桥各桥墩具有较强的抵抗地震破坏的能力，而其中最容易发生地震损伤的桥墩为制动墩，在地震动PGA水平相一致条件下，其破坏概率比其他桥墩破坏概率明显大；

2) 对于普通球型钢支座，在0.3(抗震烈度为8度)时发生轻微损伤、中等损伤的概率分别为小于40%，介于10%～20%之间，而剩余2种损伤状态对应损伤概率则均接近0；各支座构件易损性概率均比对应的桥墩构件更大。这表明连续梁桥各球型钢支座在地震作用下发生轻微和中等损伤现象较为突出，发生严重损伤和完全破坏灾害的可能性较小，而支座构件在地震中比桥墩构件更容易出现损伤。

由图7分析表明：

1) 对于安装减隔震支座的桥墩，在PGA=0.3(即抗震烈度为8度)时，各桥墩的轻微损伤概率<21%，中等损伤状态的破坏概率<11%，而剩余2级损伤状态的损伤概率约等于0。这同样反映出本文桥梁具有较强的抵抗地震破坏的能力，这与安装普通球型钢支座分析所得结论一致，然而与采用普通球型钢支座的桥墩相比，采用减隔震支座后各桥墩构件地震易损性相差较小，这主要是由于减隔震支座水平承载能力达到竖向承载能力的20%，这与球型钢支座的水平承载能力差别较大，使得各桥墩的分配较为均匀，各桥墩易损概率相差较小；

2) 对于各桥墩减隔震支座，其损伤概率相差较小，在0.3(抗震烈度为8度)时发生轻微损伤的概率低于32%，发生中等损伤的概率低于15%，这表明了对于减隔震支座仅易发生轻微破坏；对比各桥墩及其对应的支座构件的易损性概率可得，支座构件比桥墩构件更易损坏，这与球型钢支座条件下的计算结果一致。

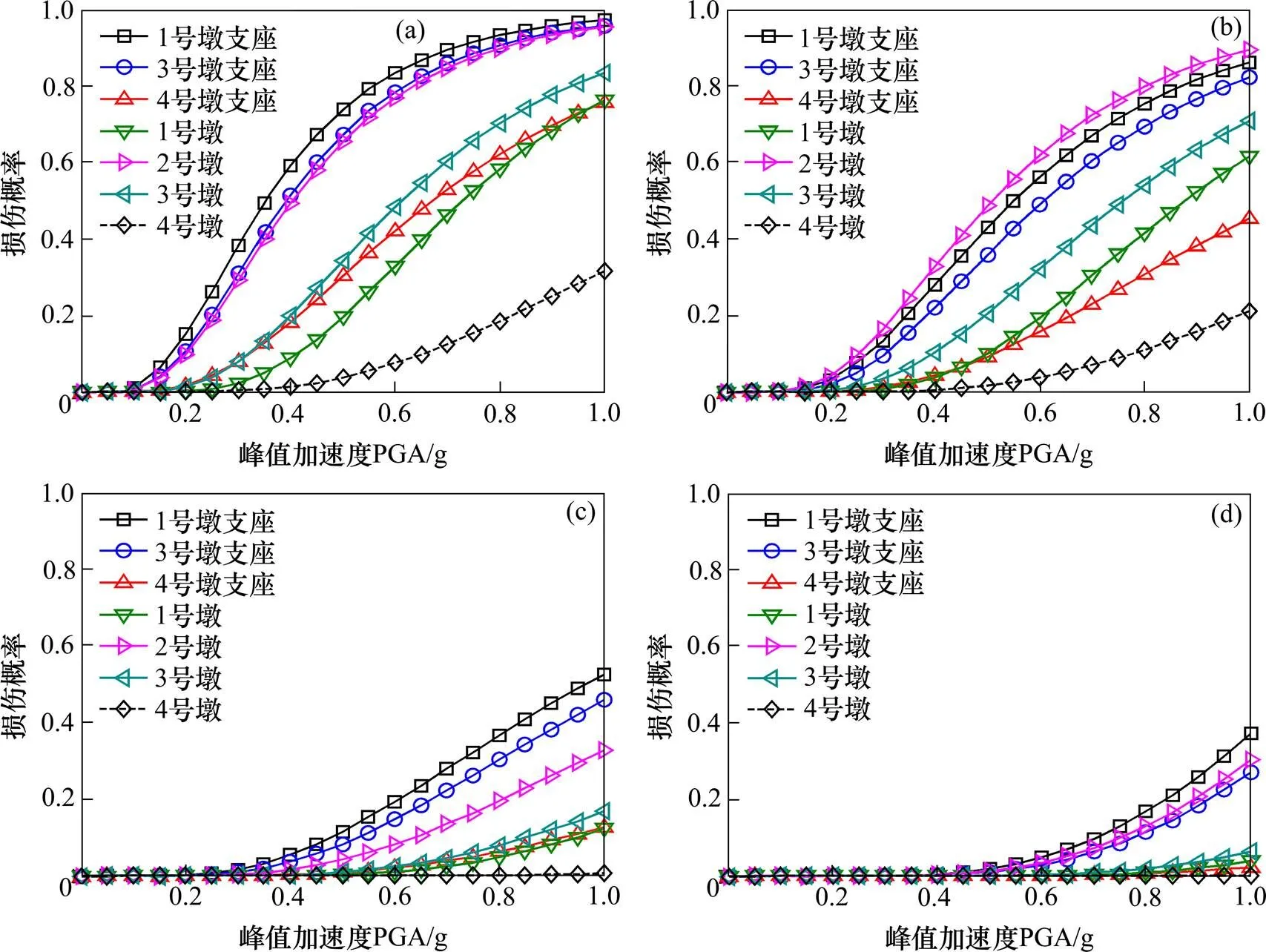
(a) 轻微损伤；(b) 中等损伤；(c) 严重损伤；(d) 完全破坏

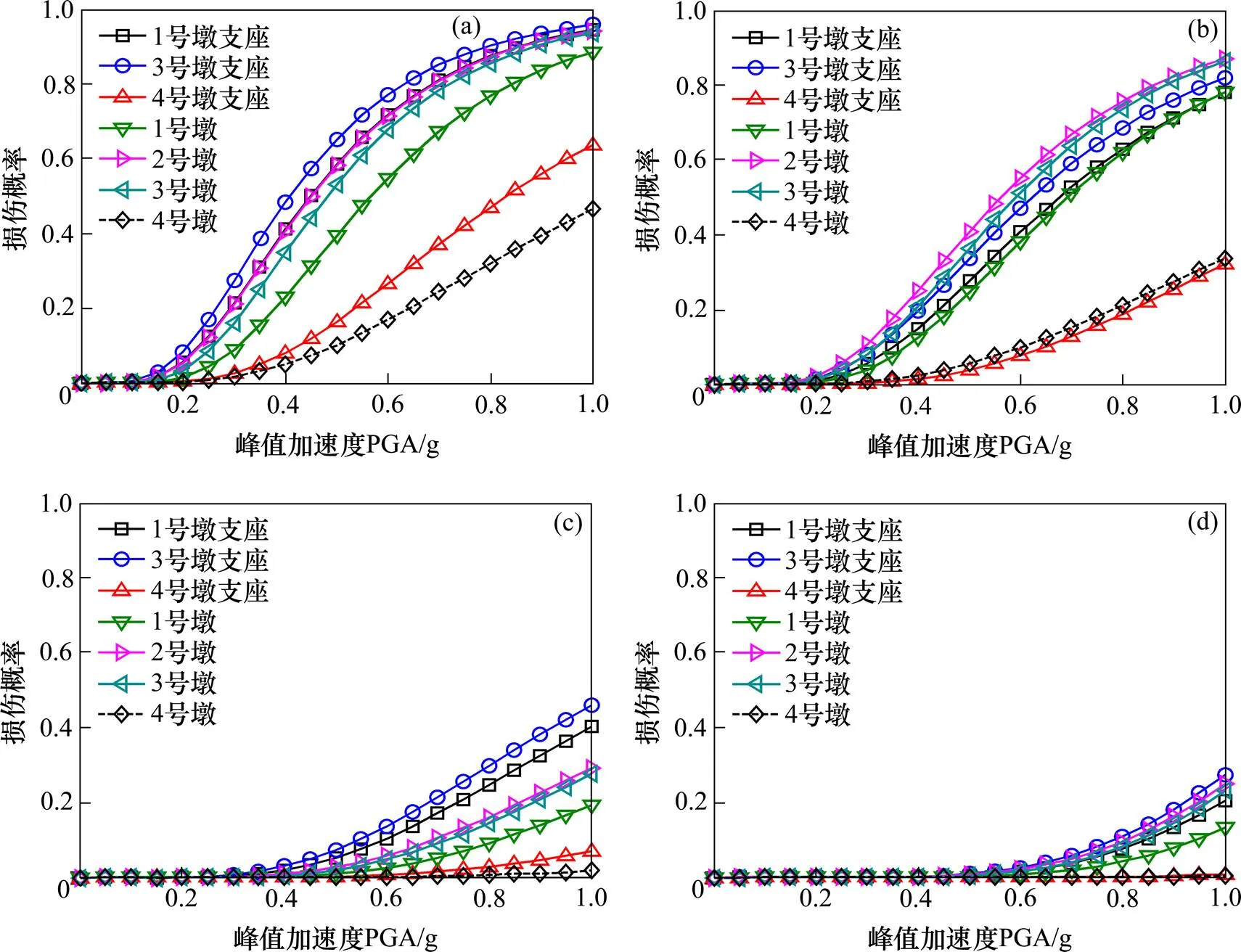
(a) 轻微损伤；(b) 中等损伤；(c) 严重损伤；(d) 完全破坏

3) 采用减隔震支座能够有效降低结构易损性概率，这主要是由于双曲面球型减隔震支座是基于摩擦滑移耗能技术的一种隔震装置，利用自身重力作用和圆弧滑动面可在地震结束后自动复位。支座自振周期仅与滑道半径有关而不受上部承载重量的影响，在地震作用时能够通过滑块往复摩擦耗能消耗地震输入能，减少地震能量向上部结构的传递，从而在地震中对结构起到保护作用。

3 结论

1) 渝昆高铁典型三跨连续梁桥的桥墩具有强抵抗地震破坏的能力，满足8度地震区抗震设防要求。制动墩、非制动墩发生轻微损伤概率分别不大于30%，10%，而所有桥墩大概率不发生严重损伤和完全破坏，综合分析表明渝昆高铁三跨连续梁桥不会发生因桥墩失效导致桥梁倒塌破坏的严重 震害。

2) 同等地震强度条件下，支座构件比桥墩构件更易发生损伤，这表明在地震过程中，支座构件先于桥墩发生破坏，满足铁路连续梁桥抗震设计要求。

3) 采用球型钢支座时，制动墩的易损性明显大于其他3个桥墩；而采用减隔震支座后，制动墩的易损性降低，其他3个桥墩的易损性有所增加，制动墩与非制动墩的易损概率较为接近，这表明通过设置减隔震支座，可有效调整4个桥墩构件吸收地震能量的比例，优化了这类非规则桥梁结构的抗震性能。

[1] 董俊, 单德山, 张二华, 等. 非规则连续刚构桥地震易损性分析[J]. 西南交通大学学报, 2015, 50(5): 635−642. DONG Jun, SHAN Deshan, ZHANG Erhua, et al. Seismic frragility of irregular continuous rigid frame bridge[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 635−642.

[2] Zentner I, Gündel Max, Bonfils N. Fragility analysis methods: Review of existing approaches and application [J]. Nuclear Engineering and Design, 2017, 323(1): 245− 258.

[3] Roy R. Maximum credible damage of RC bridge pier under bi-directional seismic excitation for all incidence angles[J]. Engineering Structures, 2017, 152(1): 251− 273.

[4] Dezfuli F H, Alam M S. Seismic vulnerability assessment of a steel-girder highway bridge equipped with different SMA wire-based smart elastomeric isolators[J]. Smart Materials and Structures, 2016, 25(7): 075039−075059.

[5] Lee T H, Nguyen D D. Seismic vulnerability assessment of a continuous steel box girder bridge considering influence of LRB properties[J]. Sādhanā, 2018, 43(1): 14−34.

[6] 杨恺. 考虑性能退化的V腿连续梁桥地震易损性及风险分析[D]. 西安: 长安大学, 2019. YANG Kai. Seismic vulnerability and risk analysis of V-supported continuous beam bridge with performance degradation[D]. Xi’an: Chang’an University, 2019.

[7] 吴姗姗, 向中富. 铁路简支梁桥三维地震易损性分析[J]. 铁道标准设计, 2019, 63(9): 56−62. WU Shanshan, XIANG Zhongfu. Three dimensional seismic vulnerability analysis of railway simply supported girder bridge[J]. Railway Standard Design, 2019, 63(9): 56−62.

[8] 马腾. 川藏铁路简支梁桥地震易损性及风险评估研究[D]. 成都: 西南交通大学, 2016. MA Teng. Seismic vulnerability and risk assessment research of railway simply supported girrder bridge for Sichuan-Tibet[D]. Chengdu: Southwest Jiaotong University, 2016.

[9] 王君. 基于IDA的高速铁路连续梁桥地震易损性研究[D]. 兰州: 兰州交通大学, 2017. WANG Jun. Seismic fragility study on the continuous beam bridge over high-speed railway based on IDA methon[D]. Lanzhou: Lanzhou Jiaotong University, 2017.

[10] Cornell A C, Jalayer F, Hamburger R O. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Structural Engineering, 2002, 128(4): 526−532.

[11] Padgett J E, DesRoches R. Methodology for the development of analytical fragility curves for retrofitted bridges[J]. Earthquake Engineering Structural Dynnmics, 2008, 37(8): 1157−1174.

[12] Kent D C, Park R. Flexural members with confined concrete[J]. Journal of the Structural Division, 1971, 97(7): 1969−1990.

[13] Itsuki Kawata, Takashi Hiraide, Kazuki Shibanuma, et al. Development of cleavage fracture initiation model for bainite steels based on micromechanism[J]. International Journal of Offshore & Polar Engineering, 2016, 26(3): 278−286.

[14] 魏标, 刘义伟, 蒋丽忠, 等. 地震作用下双曲面球型减隔震支座在铁路简支梁桥中的动力行为[J]. 土木工程学报, 2019(6): 110−118. WEI Biao, LIU Yiwei, JIANG Lizhong, et al. Dynamic behaviors of double spherical isolation bearing in simply-supported railway bridges under earthquakes[J]. China Civil Engineering Journal, 2019(6): 110−118.

[15] TB/T 2331—2004, 铁路桥梁盆式橡胶支座[S]. TB/T 2331—2004, Pot bearing for railway bridge[S].

[16] 韩国庆, 蒋丽忠, 魏标,等. 有砟轨道对典型单线铁路简支梁桥地震响应的影响[J]. 铁道科学与工程学报, 2019, 16(3): 690−697. HAN Guoqing, JIANG Lizhong, WEI Biao, et al. Effects of ballast track structure on seismic responses of simply supported bidges in a single line railway[J]. Journal of Railway Science and Engineering, 2019, 16(3): 690−697.

[17] 鲜国, 魏标, 李传富, 等. 考虑跨数影响的单线铁路简支梁桥桥墩地震响应[J]. 铁道科学与工程学报, 2019, 16(3): 148−155. XIAN Guo, WEI Biao, LI Chuanfu, et al. Effects of span numbe on seismic responses of simply supported bridge piers in a single line railway[J]. Journal of Railway Science and Engineering, 2019, 16(3): 148−155.

[18] Burratti N. A Comparison of the performances of various ground motion intensity measures[C]// 15th World Conference on Earthquake Engineering, 2012: 1−10.

[19] Nielson B G. Analytical fragility curves for highway bridges in moderate seismic zones[D]. Atlanta: GA Georgia Institute of Technology, 2005.

[20] Mehdizadeh M. Uncertainty treatment in performance based seismic assessment of typical bridge classes in united states[D]. Orlando: The University of Central Florida, 2014.

[21] 董俊. 铁路高墩大跨刚构—连续组合体系桥梁近场地震易损性分析研究[D]. 成都: 西南交通大学, 2016. DONG Jun. Fragility analysis of railway long span rigid frame-continuous combination system bridge with high pier subjected to near-fault ground motion[D]. Chengdu: Southwest Jiaotong University, 2016.

Seismic vulnerability analysis of typical continuous girder bridges of Chongqing-Kunming high-speed railway

HU Dongyang

(Kunming Survey, Design and Research Institute Co., Ltd. of CREEC, Kunming 650200, China)

In order to evaluate the seismic performance of a typical three-span continuous girder bridge of Chongqing-Kunming high-speed railway, the theoretical seismic vulnerability of the bridge is analyzed based on the method of probabilistic seismic demand analysis. The measured ground motion records along the Chongqing-Kunming high-speed railway were selected as the seismic input. Considering the uncertainty of the bridge parameters, the Latin hypercubic sampling method was used to generate the bridge finite element model samples. Based on the incremental dynamic analysis method, the seismic response peak of each component of the bridge was obtained by performing nonlinear time history analysis. The seismic demand model was established by linear regression analysis of peak response and peak acceleration of ground motion. Furthermore, the seismic vulnerability curves of the bridge structure with ordinary spherical steel bearing and hyperboloid spherical seismic isolation bearing were compared. The results show that the seismic isolation bearing can effectively reduce the vulnerability probability of the brake pier and optimize the seismic performance of irregular bridge structures with different pier heights. The research methods and conclusions can provide reference for seismic design of irregular continuous girder bridges.

continuous beam bridge; seismic vulnerability; seismic isolated bearing; Chongqing-Kunming railway

P315.9

A

1672 − 7029(2021)02 − 0297 − 09

10.19713/j.cnki.43−1423/u.T20200265

2020-04-05

四川省重点研发计划资助项目(2019YFG0048)；中国中铁二院科研资助项目(KYY2018059(18-20))

户东阳(1985−)，男，河南方城人，高级工程师，从事大跨桥梁抗震设计研究；E−mail：1506696182@qq.com

(编辑 蒋学东)