基于缺口应力的波形钢腹板结构疲劳分析研究

黄继荣，王明俊，杨慧，李立峰

基于缺口应力的波形钢腹板结构疲劳分析研究

黄继荣1，王明俊1，杨慧1，李立峰2

(1. 广州市中心区交通项目管理中心，广东 广州 510000；2. 湖南大学 土木工程学院，湖南 长沙 410082)

基于现行规范对波形钢腹板结构的疲劳问题没有明确的规定，为了研究这种结构的疲劳设计及评估方法，对试验模型梁进行等幅疲劳荷载试验，得到波形钢腹板梁典型疲劳细节和基础疲劳数据。应用有限元软件建模，采用子模型法计算细节处缺口应力，并采用缺口应力法对试验梁的疲劳性能进行评估。研究结果表明：缺口应力法评估波形钢腹板疲劳性能是可行的。波形钢腹板典型疲劳细节的缺口应力集中系数受腹板转角半径和波折角度影响较大，随腹板转角半径的增大而减小，随腹板波折角度的增大而增大。

桥梁工程；疲劳性能；缺口应力；波形钢腹板结构；模型试验

波形钢腹板组合梁桥充分发挥各种材料性能，其受力明确、跨越能力大[1]，目前已广泛应用。在实桥工程中，人们发现波形钢腹板梁构造细节处容易出现疲劳开裂，因此其结构构造细节处的疲劳设计与评估非常重要。Harrison[2]于1965年首次进行了波形钢腹板钢梁的疲劳试验。Korashy于1979年发现波形钢腹板钢梁斜向折板与翼缘板连接处发生了应力集中。Ibrahim等[3−6]于2006年进行了多片波形钢腹板钢梁的疲劳试验。随后，Kövesdi等[7]研究了波形钢腹板钢梁的疲劳性能，普遍认为：疲劳裂纹萌生于波折钢腹板的斜线段与翼缘钢板结合部位的焊趾处；影响典型细节疲劳性能的主要几何参数为钢腹板的波折角度和转角半径。波形钢腹板组合梁的疲劳性能研究是在波形钢腹板钢梁研究的基础上延续而来。在国外，日本学者对波形钢腹板组合梁的疲劳性能进行过探讨。在国内，李立峰等[8−9]对波形钢腹板组合箱梁进行了疲劳性能试验研究，并运用名义应力法和断裂力学法对其典型疲劳细节进行了疲劳分析。由于波形钢腹板梁在波形腹板与翼缘钢板连接部位的焊缝处应力分布情况极为复杂，很难对其名义应力有清晰的定义，同时由于现存的关于波形钢腹板梁疲劳试验样本量少，尚未明确其疲劳细节类别。因此，采用名义应力法评估波形钢腹板梁疲劳性能，其理论依据和试验数据支持并不充足。缺口应力法能克服了上述方法的不足，适用于复杂构造的疲劳性能评估[10]。针对上述问题，本文首先介绍缺口应力的基本原理和运用方法。接着，描叙所进行的波形钢腹板组合梁疲劳试验。然后，建立试验梁有限元模型，计算构造细节处的缺口应力，并采用缺口应力法进行疲劳性能评估。最后，进行构造细节参数分析，确定了波形钢腹板结构疲劳性能的主要影响因素。

1 缺口应力法

1.1 缺口应力

如图1所示，典型焊头表面应力分为3个区域，名义应力区离焊趾较远；随后为热点应力区，此区域内应力渐增；最后当靠近焊趾时，应力快速增加，并在焊趾处的缺口达到最大值，定义为缺口应力。

1.2 IIW的计算规定

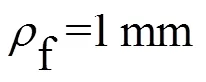
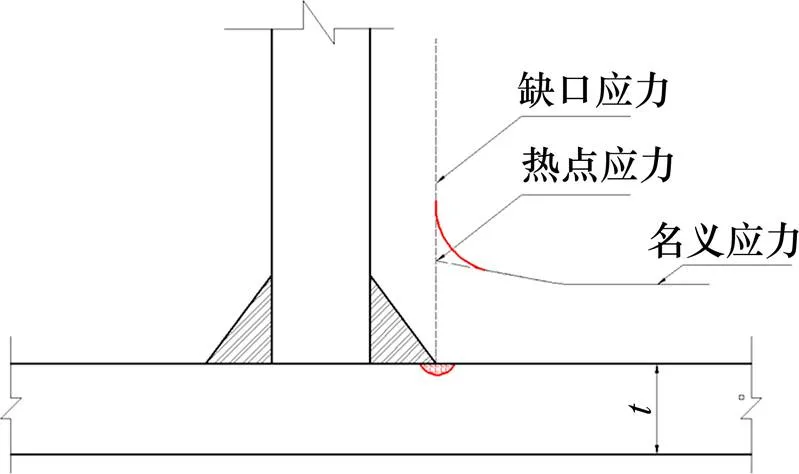
图1 焊接接头的表面应力分布

图2　缺口处的虚拟圆

采用有限元法对焊缝处的缺口虚拟圆进行模拟时，IIW国际焊协对此处的网格划分和单元尺寸大小给出了推荐值，见表1。

表1 单元划分推荐值

1.3 缺口应力S-N曲线

如图3所示，IIW规范[11]规定：缺口应力法用一条-曲线评价各种不同类别典型细节的疲劳强度。缺口应力采用正应力分析时，荷载次数小于107次，疲劳曲线斜率采用3；荷载次数大于107次后，疲劳曲线斜率采用22。当虚拟缺口半径f=1 mm时，典型疲劳细节的疲劳强度(荷载次数200万次)为225 MPa。

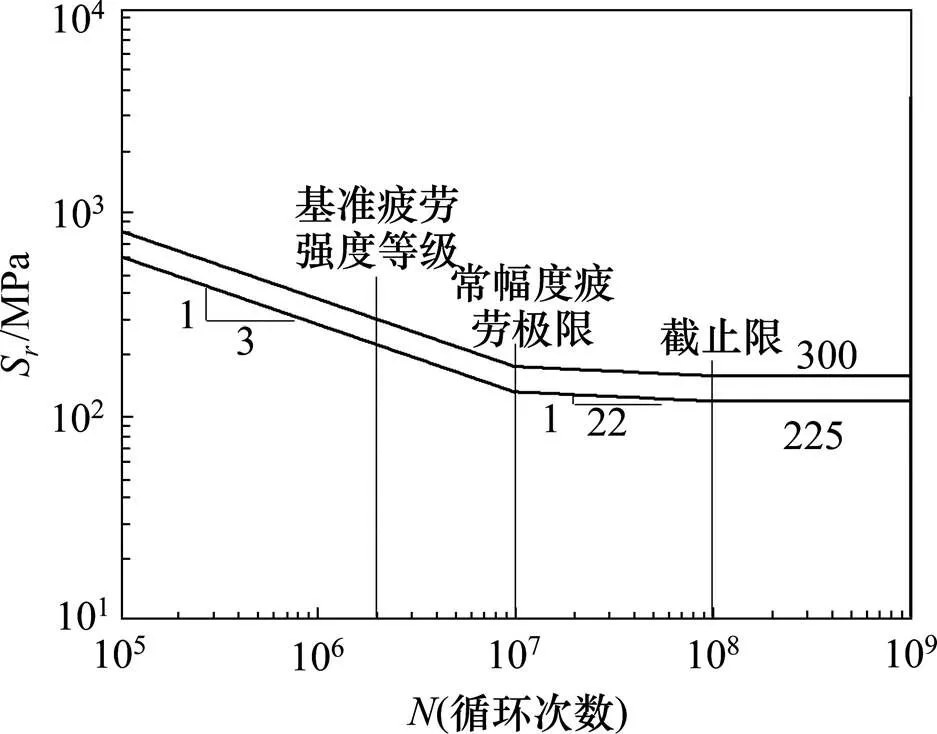
图3 标准缺口应力S-N曲线(IIW)

2 疲劳试验

2.1 试验模型梁

试验建造了8根波形钢腹板简支梁(图4～6)，梁长和净跨分别为4.2 m和4.0 m；翼板及横隔板混凝土为C50；钢腹板和翼缘钢板为Q345钢板，板厚分别为4 mm和6 mm；顶板构造钢筋为φ8，底板普通钢筋为12，钢绞线为φj 15.2。剪力连接件为翼缘型。材料各试验指标见表2。

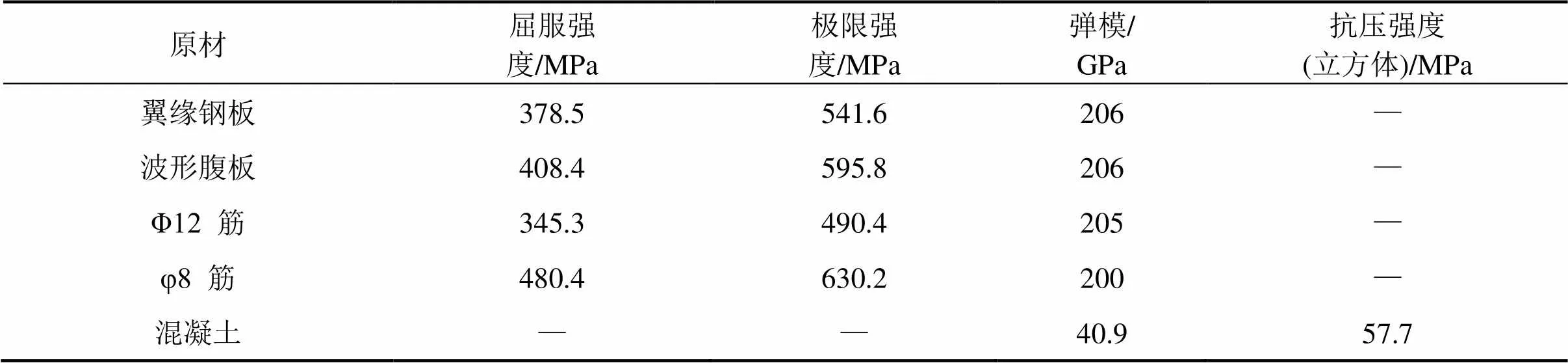
表2 材料性能指标

波形钢腹板一次性压制成型。波形钢腹板与翼缘钢板结合采用全熔透焊进行焊接。混凝土为预拌混凝土。体外预应力筋分级张拉。

2.2 疲劳试验结果

本次试验对7根试验梁进行了等荷载幅疲劳试验。本试验采用中横隔板处对称加载，疲劳试验采用PMS-500脉动疲劳机加载，加载频率采用2～4 Hz。

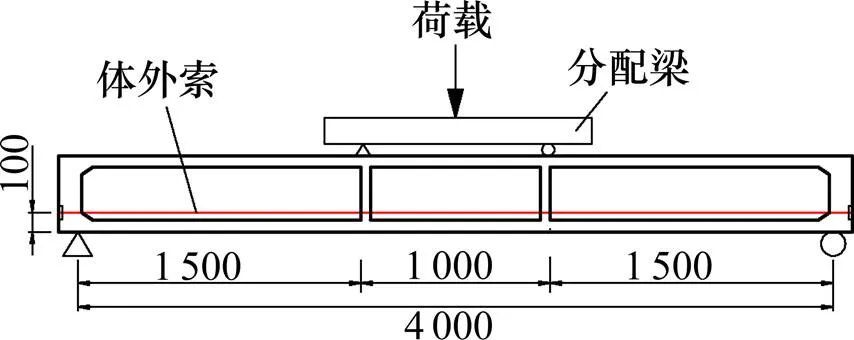
单位：mm

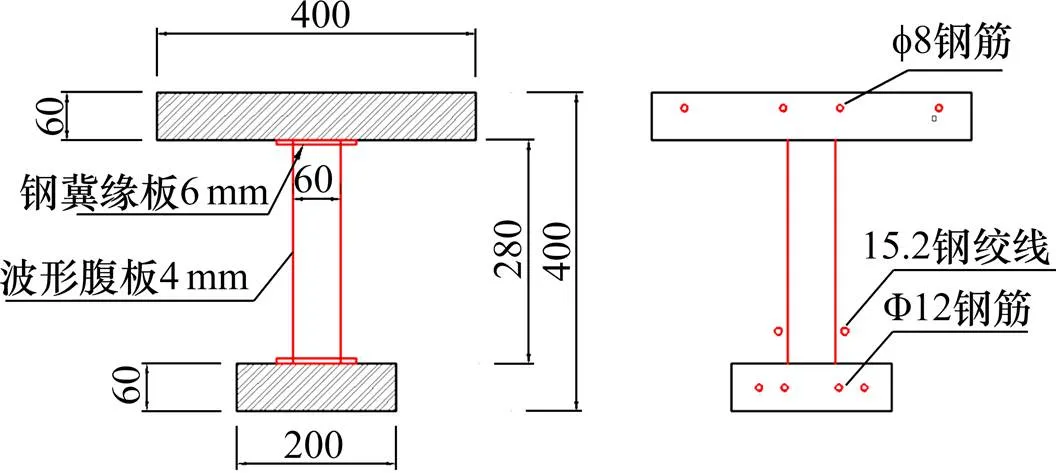
单位：mm

图7 典型疲劳破坏特征

典型疲劳破坏特征如图7所示，当荷载作用一定次数后，在位于钢腹板斜折板与翼缘钢板焊接位置的焊趾处首先萌生，并较快向两侧延展至翼缘钢板边缘，直至断裂。试验记录了7根试验梁在等幅疲劳荷载作用下，下部翼缘钢板应力幅值和其发生疲劳断裂时的荷载循环次数(疲劳寿命)，具体试验结果见表3。

表3 疲劳试验数据

3 波形钢腹板梁的缺口应力分析

3.1 模型梁的缺口应力分析

有限元模型的建立与网格划分如图8所示。波形钢腹板建模时采用了子模型技术对关键细节进行局部细化，子模型建模时切割边界远离了应力集中区域。由于本文建模采用了子模型技术对焊缝细节处进行处理，其焊缝细节处的边界条件得到了较好的保证，其计算结果与试验模型梁的应力状态更为一致。同时，建模采用了六面体单元和四面体单元2种单元进行对比，六面体单元质量值为0.63，四面体单元质量值为0.86，建模单元最终选用了质量较好的四面体单元。采用2套不同的网格尺寸进行了网格无关性验算以确保有限元计算结果的准确性。其中，方案1和方案2沿焊趾缺口区域的单元尺寸分别为0.05 mm和0.03 mm，单元网格大小均满足规范要求。

图8 试验梁有限元模型和子模型

如图9所示，有限元建模施加外荷载时，对底板和顶板分别施加100 MPa的拉压应力。

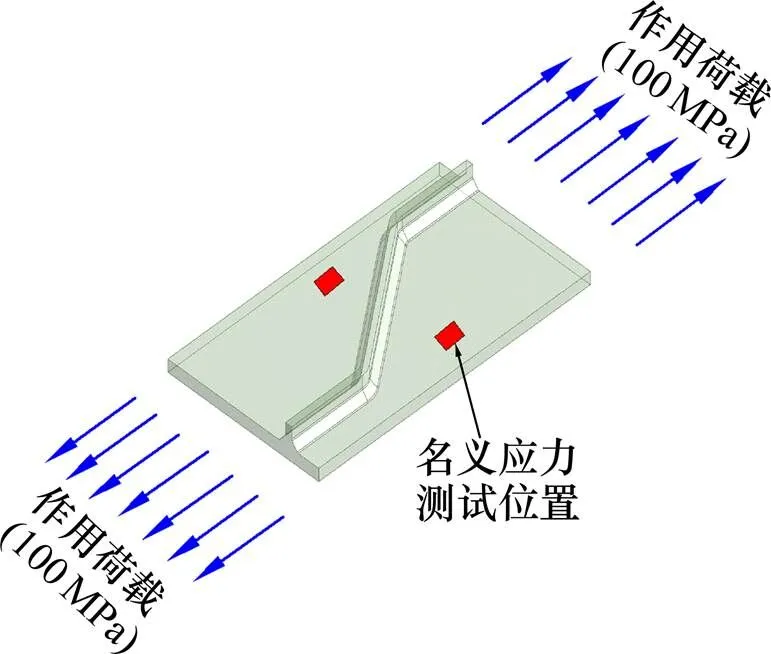
图9 模型梁翼缘钢板受力示意图

通过上述方法建模分析可得出模型梁的缺口应力，然后采用式(1)计算得到缺口应力集中系数()。

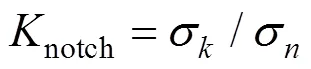
有限元缺口应力分析和应力集中系数计算结果如表4所示。从表中可知在文中有限元模型的网格密度的改变对计算结果影响非常小，建模网格精度满足网格无关性要求。同时可以看出，翼缘板名义应力测试值小于施加的荷载值(100 MPa)，说明波形钢腹板实际是对纵向应力有一定的分担作用，但是分担量较小，实际工程运用中可以忽略不计。

表4 试验梁缺口应力计算结果

3.2 试验梁的缺口应力评估

采用式(2)，将疲劳试验中得到的名义应力幅值乘以通过有限元模型计算得到的缺口应力集中系数()，就能得到疲劳试验中试验梁的缺口应力幅值。

将疲劳试验中获得的每片试验梁的疲劳寿命和与其对应的缺口应力幅值列于图10中。从图中可以看出，试验梁的缺口应力疲劳数据点都处于225 MPa 疲劳曲线的上方。用缺口应力法评价波形钢腹板结构疲劳性能具备较大的试验保证率。

4 参数分析

构造局部的应力状态往往决定了结构整体的疲劳强度。波形钢腹板梁的几何参数的改变将会较大的影响构造细节的局部应力状态。为了得到波形钢腹板结构应力状态的主要影响因素，本节将通过有限元建模，探讨了翼缘钢板厚度、波折角度、转角半径3个几何参数对波形钢腹板梁局部应力状态的影响。有限元建模方式与上节相同，采用了整体子模型法，建模具体的参数如图11和表5所示。有限元模型梁模拟的受力状态为纯弯受力，施加的外荷载为顶底板分别施加100 MPa压拉应力。有限元模型网格大小为0.05 mm。测试名义应力位置为斜板中部的翼缘钢板上，距离翼板边缘2 cm，与试验梁名义应力测试位置一致。

表5 焊接接头参数

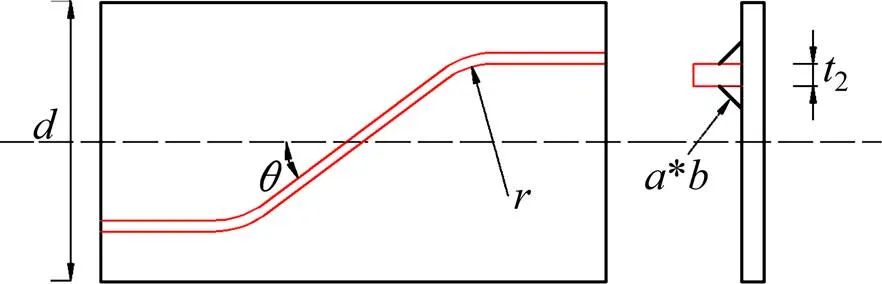
图11 焊头示意

4.1 翼缘钢板厚度变化

如图12所示，翼缘钢板厚度1从 6 mm 到 21 mm逐渐变化，其他参数保持与表5中数值不变。计算结果列于表6中。

由图表分析可以得出：波形钢腹板梁缺口应力集中系数受翼缘钢板厚度影响较小，总体保持稳定。

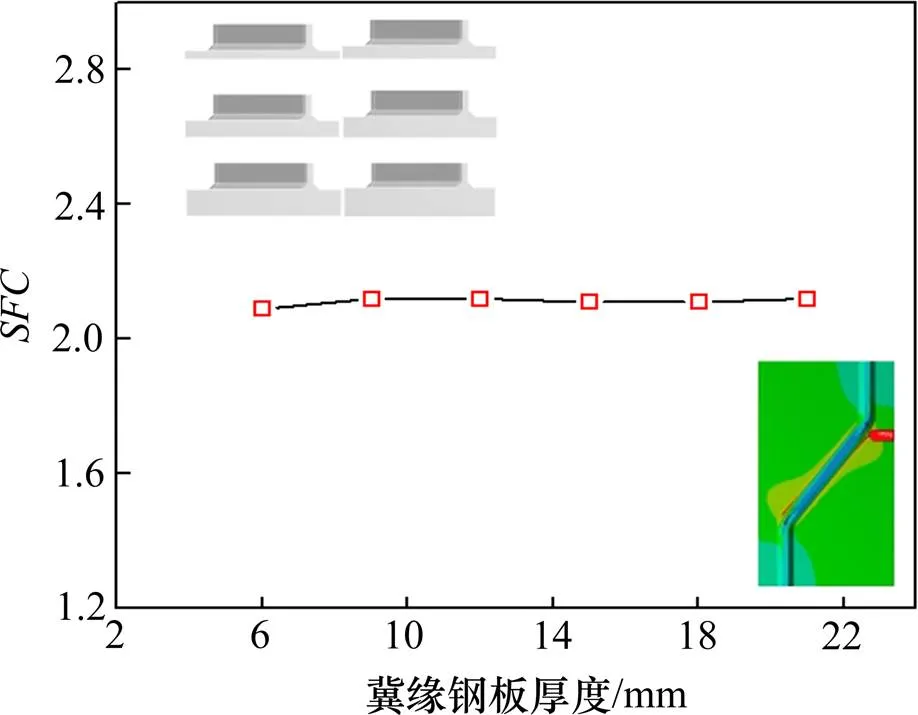
图12 应力集中系数−翼缘钢板厚度

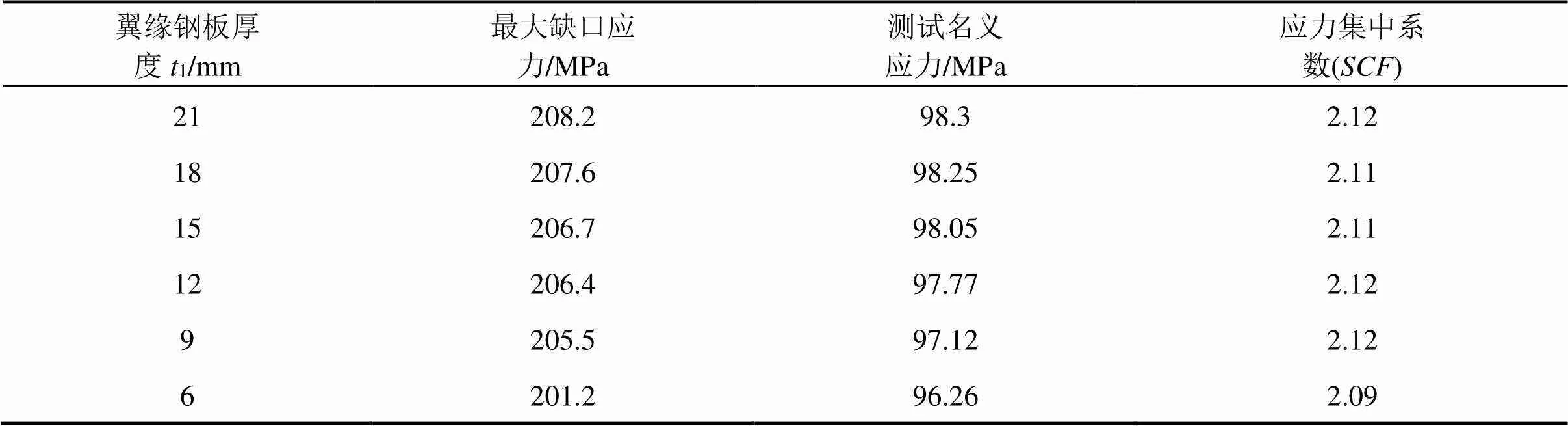
表6 应力集中系数−翼缘钢板厚度

4.2 转角半径变化

如图13所示，转角半径从10 mm 到120 mm逐渐变化，其他参数保持与表5中数值不变。计算结果列于表7中。

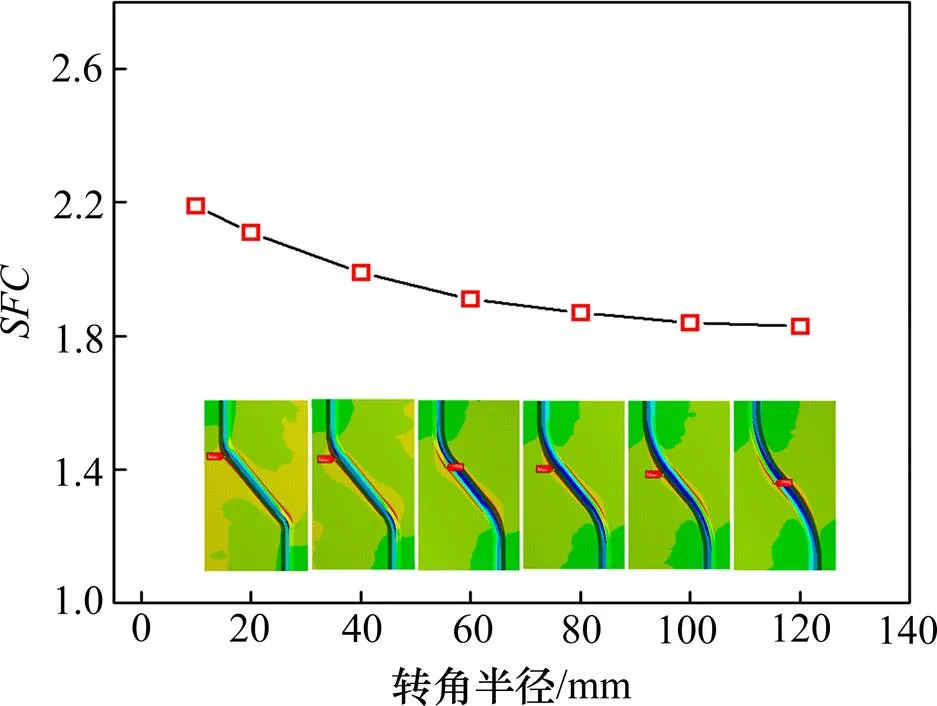
图13 应力集中系数-转角半径

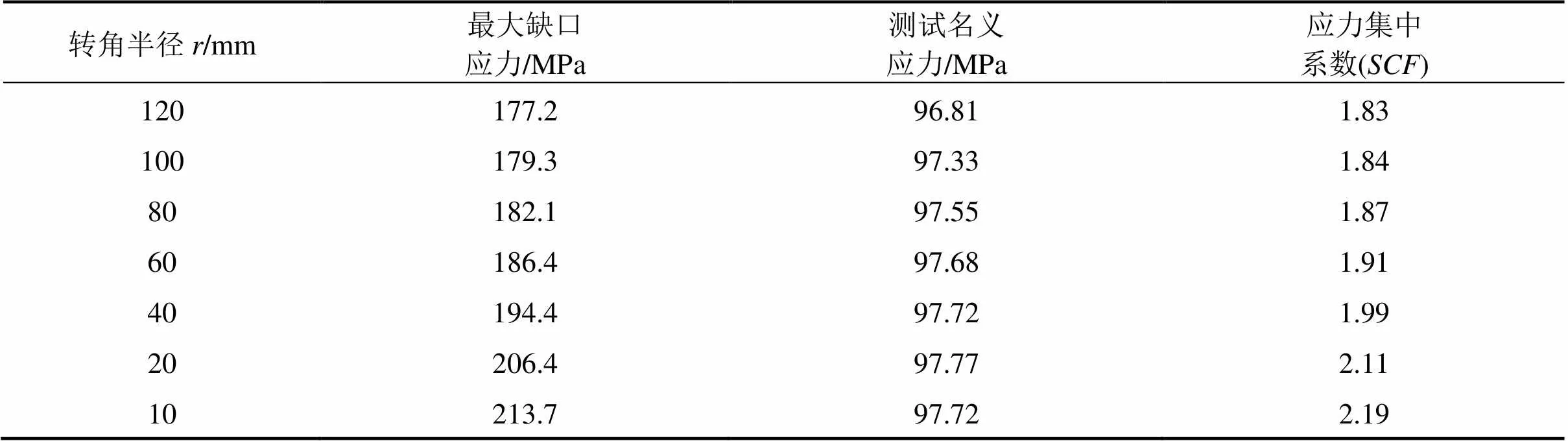
表7 应力集中系数-转角半径

由图表分析可以得出：波形钢腹板梁缺口应力集中系数受转角半径影响较大，随着转角半径的增大而减小。

4.3 波折角度变化

如图14所示，波折角度从 30°到90°逐渐变化，其他参数保持与表5中数值不变。计算结果列于表8中。

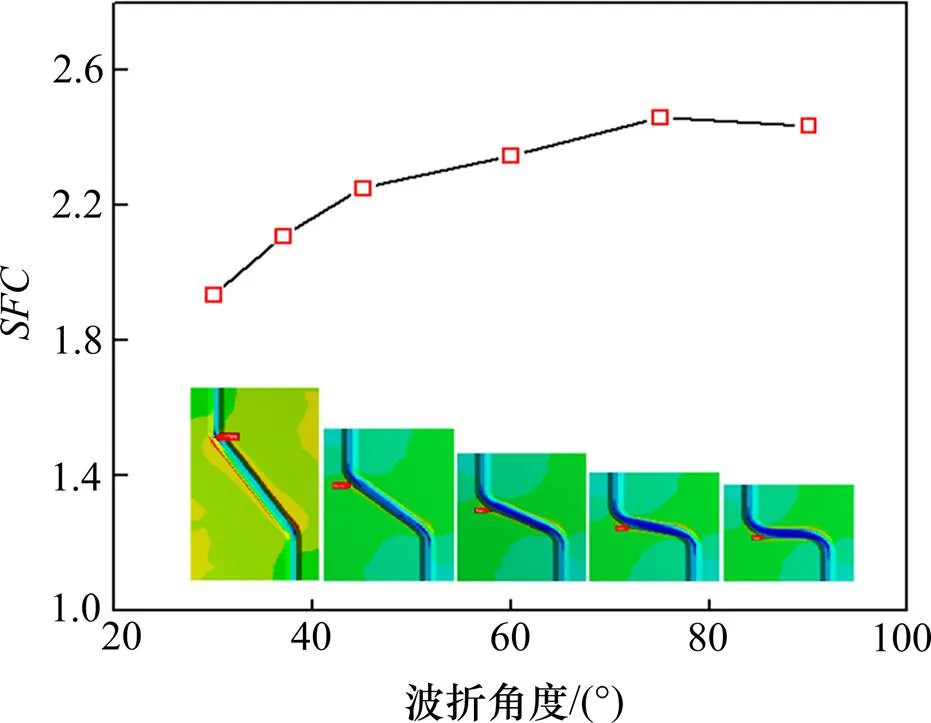
图14 应力集中系数−波折角度

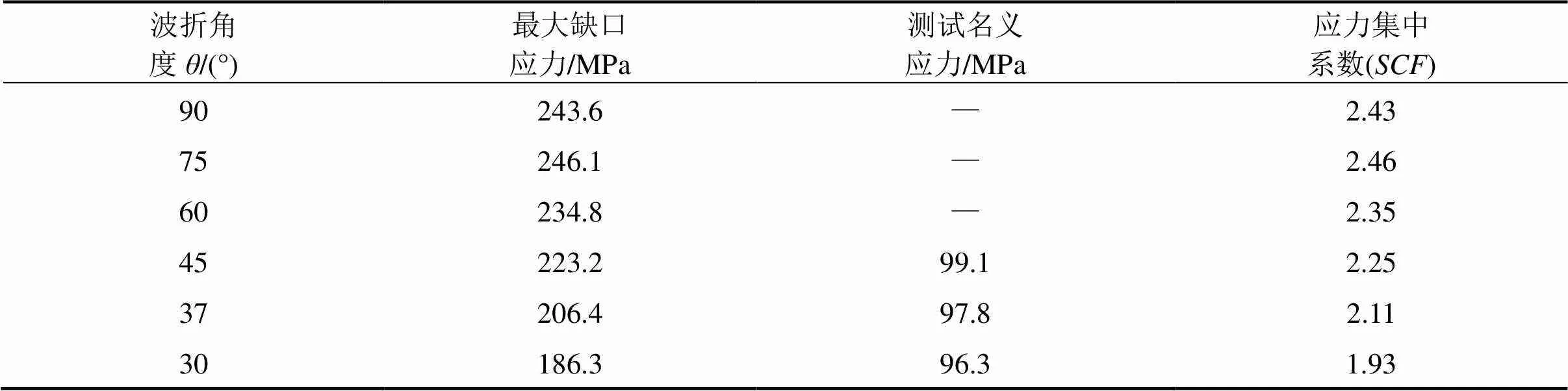
表8 应力集中系数-波折角度

由图表分析可以得出：波形钢腹板梁缺口应力集中系数受波折角度影响较大，随着波折角度的增大而增大。

5 结论

1) 有限元缺口应力分析表明模型梁最大缺口应力位置位于钢腹板斜折板靠近转角处与翼缘钢板焊接位置的焊趾处，与试验梁疲劳裂纹萌生位置基本一致。

2) 本文试验梁疲劳裂纹萌生于钢腹板斜折板靠近转角处与翼缘钢板焊接位置的焊趾处，基于波形钢腹板梁疲劳试验数据，对波形钢腹板典型疲劳细节进行了缺口应力评估，评估结果表明缺口应力法能较好的对波形钢腹板疲劳细节进行疲劳评估。

3) 缺口应力的参数分析表明：波形钢腹板典型疲劳细节的缺口应力集中系数受腹板转角半径和波折角度影响较大，随腹板转角半径的增大而减小，随腹板波折角度的增大而增大。

[1] 王志宇, 王清远, 陈宜言, 等. 波形钢腹板梁疲劳特性的研究进展[J]. 公路交通科技, 2010, 27(6): 64−71. WANG Zhiyu, WANG Qingyuan, CHEN Yiyan, et al. Research progress of fatigue behavior of corrugated web girders[J]. Journal of Highway and Transportation Research and Development, 2010, 27(6): 64−71.

[2] Harrison J D. Exploratory fatigue tests on two girders with corrugated webs[J]. British Welding Journal, 1965, 12(3): 121−125.

[3] Ibrahim S A, EL-Dakhakhni W W, Elgaaly M. Fatigue of corrugated-web plate girders: experimental study[J]. Journal of Structural Engineering, 2006, 132(9): 1371− 1380.

[4] Ibrahim S A, EL-Dakhakhni W W, Elgaaly M. Fatigue of corrugated-web plate girders: Analytical study[J]. Journal of Structural Engineering, 2006, 132(9): 1381−1392.

[5] Anami K, Sause R, Abbas H H. Fatigue of web-flange weld of corrugated web girders: 1. Influence of web corrugation geometry and flange geometry on web-flange weld toe stresses[J]. International Journal of Fatigue, 2005, 27(4): 373−381.

[6] Sause R, Abbas H H, Driver R G, et al. Fatigue life of girders with trapezoidal corrugated webs[J]. Journal of Structural Engineering, 2006, 132(7): 1070−1078.

[7] Kövesdi B, Dunai L. Fatigue life of girders with trapezoidally corrugated webs: an experimental study[J]. International Journal of Fatigue, 2014, 64: 22−32.

[8] 李立峰, 肖小艳, 刘清. 波形钢腹板PC组合箱梁疲劳损伤对抗弯承载能力的影响研究[J]. 土木工程学报, 2012, 45(7): 111−119. LI Lifeng, XIAO Xiaoyan, LIU Qing. Study on the residual flexural capacity of composite box girders with corrugated steel webs after fatigue damage[J]. China Civil Engineering Journal, 2012, 45(7): 111−119.

[9] 彭鲲, 李立峰, 肖小艳, 等. 波形钢腹板组合箱梁疲劳性能试验与理论分析[J]. 中国公路学报, 2013, 26(4): 94−101. PENG Kun, LI Lifeng, XIAO Xiaoyan, et al. Experimental and theoretical analysis on fatigue performance of composite box girder with corrugated steel webs[J]. China Journal of Highway and Transport, 2013, 26(4): 94−101.

[10] Radaj D, Sonsino C M, Fricke W. Introduction[M]// Fatigue Assessment of Welded Joints by Local Approaches. Amsterdam: Elsevier, 2006: 1−12.

[11] Hobbacher A. Recommendations for fatigue design of welded joints and components[M]. Springer International Publishing, 2016.

Study on fatigue analysis of beam with corrugated steel webs using notch stress method

HUANG Jirong1, WANG Mingjun1, YANG Hui1, LI Lifeng2

(1. Guangzhou City District Transportation Project Management Center, Guangzhou 510000, China;2. College of Civil Engineering, Hunan University, Changsha 410082, China)

There are no standards to guide the design of fillet weld’s fatigue behavior of beam with corrugated steel webs. In order to study its fatigue design and assessment methods, fatigue test was performed, and the typical fatigue detail and basic fatigue data were obtained from the test. FEM beams were established and the sub model method was adopted to calculate the stress of welding detail. The notch stress concentration factor of model beams was calculated using the method recommend by the IIW. The fatigue performance of test beams was assessed by the notch stress method, and it could be concluded that the notch stress method was a feasible method in fatigue performance assessing of the corrugated steel web beam. The parameter analysis shows that: the largest notch stress and its concentration factor will be greatly influenced by corner radius and corrugation angle and they will decrease with the increment of corner radius and increase with the increment of corrugation angle.

bridge engineering; fatigue behavior; notch stress; beam with corrugated steel webs; model test

U441+.4

A

1672 − 7029(2021)02 − 0425 − 07

10.19713/j.cnki.43−1423/u.T20200357

2020−04−27

国家自然科学基金资助项目(51978257)；花都交通局科技项目

李立峰(1971−)，男，湖南沅江人，教授，博士，从事桥梁抗震、钢桥疲劳研究；E−mail：lilifeng@hnu.edu.cn

(编辑 涂鹏)