列车动力响应的平稳性和各态历经性分析

吴梦雪，唐德发，李永乐，朱金

列车动力响应的平稳性和各态历经性分析

吴梦雪1，唐德发1，李永乐2，朱金2

(1. 西南石油大学 土木工程与测绘学院，四川 成都 610500；2. 西南交通大学 土木工程学院，四川 成都 610031)

研究列车动力响应的平稳性和各态历经性对寻求列车动力响应随机过程的统计规律具有重要意义。基于多体动力学理论，采用多体动力学分析软件Simpack建立国内某高速列车动车车辆的多体动力学模型。采用三角级数法模拟得到的轨道不平顺作为随机输入激励计算得到列车以不同速度行驶不同距离的动力响应时程样本序列。进一步运用平稳性检验方法中的逆序数检验法和单位根检验法对列车动力响应随机过程的平稳性进行检验。运用Monte-Carlo方法并结合随机过程的相关理论，计算1 500个在随机轨道不平顺激励下列车以200 km/h速度行驶1 km工况的动力响应时程样本序列的集合均值和集合相关函数，时间均值和时间相关函数，对列车动力响应的平稳性和各态历经性进行了证明。研究结果表明，列车以200 km/h的速度行驶1 km工况的动力响应可近似为具有各态历经性的平稳随机过程，即可采用一个时程响应样本来反映列车动力响应总体的统计规律。随着列车动力响应样本个数的增加，列车动力响应的平稳性和各态历经性都将更加稳定。

列车动力响应；随机过程；平稳性；各态历经性；多体动力学

列车的动力响应是典型的随机过程，目前认为其随机性主要来源于随机的轨道不平顺激励和列车系统参数的随机性[1]。针对列车动力响应的平稳性和各态历经性开展研究对寻求列车动力响应随机过程的统计规律具有极其重要的意义。列车动力响应的一个时程样本仅是统计意义上随机过程的一次实现，无法反映列车动力响应的概率统计特征，但如果列车的动力响应过程可以近似为平稳随机过程和满足各态历经性，那么就可以采用一个时程样本来反映列车通过线路时动力响应的统计规律，而无需计算大量的列车振动响应时程样本。此外，列车动力响应的平稳性也会在列车动力响应频谱分析方法的选择上具有决定性的作用。经典的傅里叶变换方法适用于平稳随机过程的频谱分析，而非平稳随机过程的时频分析则更宜采用小波分析和希尔伯特—黄变换方法。因此，列车动力响应随机过程平稳性和各态历经性的检验是可靠地评判列车振动水平(安全性和平稳性)的基本条件。近几十年来，高速铁路建设的全面推进对列车—线路耦合振动理论的研究和发展起了巨大的推动作用，许多学者针对列车—线路的随机耦合振动已开展了广泛的研究。王伟等[2]将轮轨力预估格式的迭代求解方法与子集模拟法相结合，提出了一种考虑轨道不平顺随机性的车轨耦合系统动力可靠度评估的新方法。WEI等[3]研究了轨枕和一系橡胶弹簧的温频动态特性对列车—轨道耦合振动的影响规律。李双等[4]研究了随机的悬挂参数对列车运行舒适性指标的全局灵敏度。李永乐等[5−6]将侧向风、高速列车、大跨度桥梁作为一个相互作用、协调工作的耦合系统，发展了一种较为完善的风—车—桥系统非线性空间耦合分析模型。XU等[7]提出了一种同时考虑时间和空间域的列车—轨道—桥梁随机耦合振动分析模型。XIN等[8]利用三维空间列车—轨道—桥梁耦合模型从随机不确定性的角度研究了车桥耦合系统的列车共振。TAN等[9]研究了列车运行速度和混凝土的弹性模量对列车—轨道—桥梁—桥墩耦合系统随机动力响应的影响。上述大多数研究的主要目的是建立列车—线路随机耦合振动的求解方法，或研究系统某些参数对列车—线路耦合系统动力响应的影响，从而对列车运行的安全性和旅客乘坐的舒适性加以评价，而对列车动力响应的随机特性如平稳性和各态历经性关注较少。本文采用多体动力学分析软件Simpack建立国内某高速列车动车车辆的多体动力学模型，将随机轨道不平顺样本作为输入激励，通过多体动力学仿真计算得到列车的动力响应时程样本序列。基于随机过程的相关理论，对列车动力响应随机过程的平稳性和各态历经性开展研究。本文的结论可为高速列车运行的安全性和平稳性评价以及列车动力响应频谱分析方法的选择提供参考。

1 建立模型

1.1 列车多体动力学模型

基于多体动力学理论，列车模型的各部件可通过刚体、力元和轮轨接触来描述，并通过铰、约束、力元等来定义车辆各部件之间及相对于惯性坐标系的运动关系，并最终形成动力学控制方程来描述车辆系统。以国内某高速列车动车车辆为原型，运用专业的多体动力学分析软件Simpack建立了相应的多体动力学模型。模型中车体、转向架、轮对、轴箱具有很大刚度，在分析中不考虑其弹性变形视为刚体。一、二系弹簧、减振器等采用弹簧—阻尼力元进行模拟，全车共计50个自由度。列车主要参数以及列车—轨道系统的空间耦合模型分别如表1和图1所示。

模型中一、二系悬挂、扭杆弹簧和轴箱转臂弹簧均采用线性5号力元进行模拟，而横向止挡采用非线性5号力元进行模拟。一系垂向减振器、二系横向减振器、抗蛇行减振器均采非线性6号力元进行模拟。扭杆弹簧采用13号力元进行模拟。充分考虑了模型中力元的非线性特性，限于篇幅各力元的力学模型详见Simpack的帮助文档。

根据文献[10]车辆多体系统的运动方程可由下式表示：

模型的轮轨法向力采用Herz理论计算，蠕滑力采用FASTSIM算法求得。运用Simpack软件建立的列车—轨道系统多体动力学模型如图2所示。

表1 列车模型主要参数

(a) 侧视图；(b) 端视图

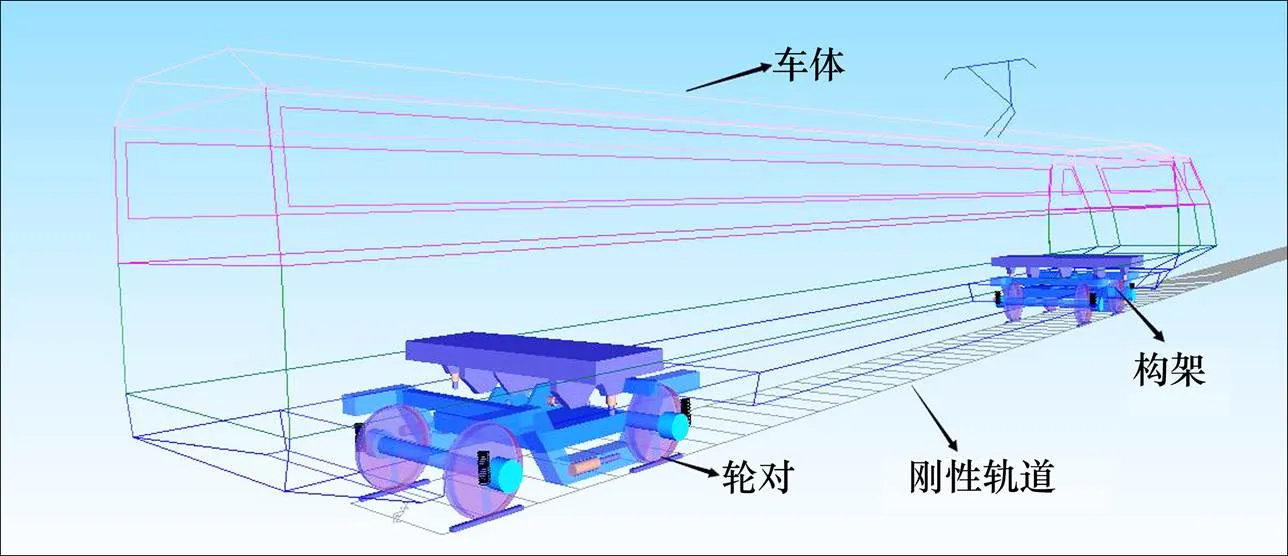
图2 列车—轨道系统多体动力学模型

1.2 轨道不平顺

轨道不平顺是由于在铁路线路的平直段，钢轨并不是呈理想的平直状态，2根钢轨在高低和左右方向相对于理想的平直轨道会存在偏差，这种几何参数的偏差即为轨道不平顺[11]。轨道不平顺是列车—轨道系统的主要激振源，也是引发列车随机振动的主要原因。因此，本文对列车动力响应随机特性的研究仅把轨道不平顺作为列车—轨道系统的输入激励。列车的轨道不平顺主要分为垂向不平顺、方向不平顺、水平不平顺、轨距不平顺4种。本文的轨道不平顺谱选用德国低干扰谱，可采用三角级数法对轨道不平顺序列进行模拟。原理如式(2) 所示：

运用三角级数法模拟得到的轨道不平顺的功率谱密度与目标谱的吻合情况如图3所示，可见模拟的功率谱与目标谱吻合较好。

2 平稳性检验

数据的平稳性检验方法较多，常用的平稳性检验方法有逆序数检验法、轮次检验法、单位根(Augmented Dickey-Fuller test, ADF)检验法、KPSS (Kwiatkowski-Phillips-Schmidt-Shin test)检验法等。目前一些学者还提出了一些平稳性检验的新方法，杨栋等[12]提出了一种基于递归分析的振动信号非平稳性评价方法，马麟等[13]运用基于Hilbert-Huang变换的时频分析方法来描述大跨度桥梁非线性抖振响应的非平稳性。为探究列车行驶不同里程长度动力响应的平稳性，本文以常见的2种平稳性检验方法逆序数检验法和单位根(ADF)检验法对列车以200 km/h速度行驶不同距离(100～1 000 m)时动力响应的平稳性进行检验，检验结果如表2所示。

图3 模拟谱与目标谱的对比(垂向不平顺)

逆序数检验法是一种非参数检验方法，其检验结果可能受到分段数的影响[14]。当列车行驶距离为100 m时，列车车辆的横向加速度响应仅在分段数为20时检验结果为平稳，因此认为该检验结果可能受到分段数的影响而产生误判。由表2平稳性的检验结果可以发现，逆序数检验法的检验结果可能受到分段数的影响，甚至产生误判。而单位根检验法的检验结果不受分段数的影响，检验结果更稳定。因此，可以认为列车以200 km/h速度行驶100 m时的横向加速度响应为非平稳的随机过程。

上述检验结果表明，列车以200 km/h运行，横向加速度响应在列车行驶距离小于200 m时为非平稳随机过程，行驶距离大于200 m时为平稳随机过程；列车的垂向加速度响应在列车行驶距离小于300 m时为非平稳随机过程，行驶距离大于300 m时为平稳随机过程。这主要是由于轨道不平顺样本只有在空间长度较长时才被认为是平稳的随机过程。

3 理论证明

3.1 集合均值和集合相关函数

3.1.1 集合均值

根据式(3)可以求得任意位置处列车动力响应的集合均值，其表示列车动力响应在任意位置处的理论平均，所求得的列车动力响应集合均值的结果如图4、图5和表3所示。

表2 平稳性检验结果

3.1.2 集合相关函数

为具有代表性，对上述1 500个样本，分别取距离间隔d为10，50，100和500 m求得其集合相关函数如图6、图7和表4所示。

图5 列车垂向加速度集合均值

表3 列车加速度响应集合均值和时间均值统计

3.1.3 平稳性分析

根据随机过程的相关理论，当随机过程的集合均值是不随位置变化的常数，而集合相关函数与所取的具体位置无关而仅与距离间隔相关时，则该随机过程为平稳随机过程[16]。

图6 列车横向加速度集合相关函数

图7 列车垂向加速度集合相关函数

由图4、图5和表3可见，列车横向加速度响应和垂向加速度响应的集合均值均围绕一条直线波动，且标准差均小于9.9×10−3，说明集合均值仅微小波动。

图8展示了列车垂向加速度的均值标准差与样本个数之间的关系，并对集合均值和时间均值的标准差与样本个数的关系做了曲线拟合。由图8可以发现，集合均值的标准差随着样本个数的增加而逐渐减小，由此可以推断，当数据的组数足够多时，集合均值的标准差进一步减小，集合均值将为一个稳定的常数。

进一步的由图6、图7和表4可见，横向加速度和垂向加速度响应的集合相关函数在取任意距离间隔时，集合相关函数的标准差均很小，说明集合相关函数也仅存在微小波动，故可以认为集合相关函数与列车所处的具体位置无关；而当取不同的距离间隔时，集合相关函数的波动中心不同，所以集合相关函数的取值与距离间隔相关。综上所述，集合相关函数与列车所处的具体位置无关而仅与距离间隔相关。因此，结合平稳随机过程的定义可以得到列车的动力响应可近似为平稳随机过程。

图8 均值标准差与样本个数的关系

3.2 时间均值和时间相关函数

3.2.1 时间均值

由式(5)计算得到上述1 500个列车动力响应样本的时间均值如图9、图10和表3所示。

图10 列车垂向加速度时间均值

3.2.2 时间相关函数

为不失一般性，对上述1 500个样本，依然分别取距离间隔d为10，50，100和500 m。由式(6)计算得到的时间相关函数如图11、图12和表4 所示。

3.2.3 各态历经性分析

根据随机过程的相关理论，当平稳随机过程的时间均值以概率为1等于集合均值；时间相关函数也以概率为1等于集合相关函数时，则可认为该平稳随机过程具有各态历经性[16]。

图12 列车垂向加速度时间相关函数

对比表3中集合均值和时间均值的计算结果可知集合均值和时间均值的平均值几乎相等，而集合均值和时间均值的标准差均小于9.9×10−3，说明集合均值和时间均值均仅存在微小波动。且由图8可见，列车动力响应集合均值的标准差随着样本个数的增加而逐渐减小，但时间均值的标准差几乎不发生变化，由此可以推断当数据的组数足够多时，集合均值的标准差将逐渐逼近时间均值的标准差。因此，可以近似地认为集合均值和时间均值以概率为1相等。

图13和图14给出了相关函数部分距离间隔的对比情况，再结合表4可见，时间相关函数和集合相关函数的平均值相等，仅仅是标准差存在较小的差异。虽然时间相关函数的波动较集合相关函数略大，但两者的波动范围基本吻合。因此，可以近似认为时间相关函数以概率为1等于集合相关函数。

表4 列车加速度响应集合相关函数和时间相关函数统计

图13 列车横向加速度相关函数对比

图14 列车垂向加速度相关函数对比

上述分析表明，列车以200 km/h的速度行驶1 km工况的动力响应可近似为具有各态历经性的平稳随机过程。

4 结论

1) 当列车以200 km/h速度行驶，列车横向加速度响应在列车行驶距离小于200 m时为非平稳随机过程，行驶距离大于200 m时为平稳随机过程。列车垂向加速度响应在列车行驶距离小于300 m时为非平稳随机过程，行驶距离大于300 m时为平稳随机过程。

2) 逆序数检验法的检验结果可能受到分段数的影响，甚至产生误判；而单位根检验法的检验结果不受分段数的影响，检验结果更稳定。

3) 列车以200 km/h的速度行驶1 km工况的动力响应可近似为具有各态历经性的平稳随机过程，即可采用一个时程响应样本来反映列车动力响应总体的统计规律。

4) 随着列车动力响应样本个数的增加，列车动力响应集合均值的标准差在减小，且逐渐逼近时间均值的标准差，列车动力响应的平稳性和各态历经性都将更加稳定。

[1] 徐磊, 翟婉明. 轨道不平顺概率模型[J]. 交通运输工程学报, 2018, 18(3): 56−63. XU Lei, ZHAI Wanming. Track irregularity probabilistic model[J]. Journal of Traffic and Transportation Engineering,2018, 18(3): 56−63.

[2] 王伟, 张亚辉, 欧阳华江. 考虑轨道不平顺随机性的车轨耦合系统动力可靠度分析[J]. 大连理工大学学报, 2019, 59(2): 111−117. WANG Wei, ZHANG Yahui, OUYANG Huajiang.Dynamic reliability analysis of vehicle-track coupled systems considering randomness of track irregularities[J].Journal of Dalian University of Technology,2019, 59(2): 111−117.

[3] WEI Kai, WANG Feng, WANG Ping, et al. Effect of temperature-and frequency-dependent dynamic properties of rail pads on high-speed vehicle–track coupled vibrations[J]. Vehicle System Dynamics, 2017, 55(3), 351−370.

[4] 李双, 余衍然, 陈玲, 等. 随机悬挂参数下轨道车辆平稳性的全局灵敏度分析[J]. 铁道学报, 2015, 37(8): 29−35. LI Shuang, YU Yanran, CHEN Ling, et al.Global sensitivity analysis on the ride quality of railway vehicle with stochastic suspension parameters[J]. Journal of the China Railway Society,2015, 37(8): 29−35.

[5] 李永乐. 风—车—桥系统非线性空间耦合振动研究[D]. 成都: 西南交通大学, 2003. LI Yongle. Nonlinear three-dimensional coupling vibration of wind-vehicle-bridge system[D]. Chengdu: Southwest Jiaotong University, 2003.

[6] LI Yongle, QIANG Shizhong, LIAO Haili, et al. Dynamics of wind-rail vehicle-bridge systems[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93(6): 483−507.

[7] XU Lei, ZHAI Wanming, LI Zili. A coupled model for train-track-bridge stochastic analysis with consideration of spatial variation and temporal evolution[J]. Applied Mathematical Modelling, 2018, 63: 709−731.

[8] XIN Lifeng, LI Xiaozhen, ZHANG Jiaxin, et al. Resonance analysis of train–track–bridge interaction systems with correlated uncertainties[J]. International Journal of Structural Stability and Dynamics, 2020, 20(1): 2050008.

[9] TAN Sui, YU Zhiwu, SHAN Zhi, et al. Influences of train speed and concrete young's modulus on random responses of a 3D train-track-girder-pier coupled system investigated by using PEM[J]. European Journal of Mechanics A: Solids, 2019, 74: 297−316.

[10] 缪炳荣. SIMPACK动力学分析基础教程[M]. 成都: 西南交通大学出版社, 2008. MIAO Bingrong. SIMPACK basic course of dynamic analysis[M]. Chengdu: Southwest Jiaotong University Press, 2008.

[11] 任尊松. 车辆系统动力学[M]. 北京: 中国铁道出版社, 2007. REN Zunsong. Vehicle system dynamics[M]. Beijing:China Railway Press,2007.

[12] 杨栋, 任伟新. 基于递归分析的振动信号非平稳性评价[J]. 振动与冲击, 2011, 30(12): 39−43. YANG Dong, REN Weixin. Non-stationarity evaluating for vibration signals using recurrence plot[J].Journal of Vibration and Shock,2011, 30(12): 39−43.

[13] 马麟, 刘健新, 韩万水, 等. 基于Hilbert-Huang变换的大跨桥梁非线性抖振响应时频分析[J]. 振动与冲击, 2010, 29(11): 237−241, 265. MA Lin, LIU Jianxin, HAN Wanshui, et al.Time- frequency analysis for nonlinear buffeting response of a long-span bridge based on HHT[J].Journal of Vibration and Shock,2010, 29(11): 237−241, 265.

[14] 李传金, 杜亚楠, 游志伟, 等. 微动数据平稳性检验方法的适用性分析[J]. 地球物理学进展, 2018, 33(2): 823−829. LI Chuanjin, DU Yanan, YOU Zhiwei, et al. Applicability analysis of stationarity test methods in microtremor[J].Progress in Geophysics, 2018, 33(2): 823−829.

[15] 王志刚. 随机过程[M]. 合肥: 中国科学技术大学出版社, 2018. WANG Zhigang. Stochastic process[M]. Hefei: University of Science and Technology of China Press, 2018.

[16] 王强. 苏成. 公路桥梁随机车队的平稳性和各态历经性[J]. 华南理工大学学报(自然科学版), 2015, 43(10): 8−15. WANG Qiang, SU Cheng. Stationarity and ergodicity of random motorcade on highway bridge[J].Journal of South China University of Technology (Natural Science Edition),2015, 43(10): 8−15.

Analysis of stationarity and ergodicity of train dynamic response

WU Mengxue1, TANG Defa1, LI Yongle2, ZHU Jin2

(1. School of Civil Engineering and Geomatics, Southwest Petroleum University, Chengdu 610500, China; 2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)

It is of great significance to study the stationarity and ergodicity of train dynamic response, usually regarded as a stochastic process, in order to reveal the statistics of the train dynamic response. Firstly, a three-dimensional multi-body dynamics model of a high-speed passenger rail vehicle was established based on the multi-body dynamics theory in the multi-body dynamics analysis software Simpack. Secondly, the stochastic track irregularities were simulated using the trigonometric series method and used as the internal excitation for the established rail vehicle numerical model, with which the train dynamic responses under different running speeds and distances were obtained. Subsequently, the stationarity of the train dynamic responses was examined by both the Inverse Ordinal Number test and the Augmented Dickey-Fuller test. Finally, Monte-Carlo approach was employed to obtain 1 500 samples of train dynamic responses travelling over a distance of 1 km at a speed of 200km/h. In order to validate the stationarity and ergodicity of train dynamic responses, the statistics of the 1 500 samples, i.e., ensemble means, ensemble related functions, time-average values and time-related functions, were calculated based on the stochastic process theory. The statistical results show that the dynamic response of the train travelling over a distance of 1 km at a speed of 200 km/h can be regarded as a stationary and ergodic process. This suggests that the statistical information of one sample of the train dynamic response can be used to reflect the overall statistical law of the train dynamic response. It is also found that the stationarity and ergodicity of train dynamic response will be more stable with more samples.

train dynamic response; stochastic process; stationarity; ergodicity; multi-body dynamics

U270.11

A

10.19713/j.cnki.43−1423/u.T20200289

1672 − 7029(2021)02 − 0315 − 10

2020−04−09

国家自然科学基金资助项目(51708470)；国家杰出青年科学基金资助项目(51525804)；国家重点研发计划资助项目(2018YFC1507802)；西南石油大学科研“启航计划”资助项目(2017QHZ025)；西南石油大学桥梁安全评估青年科技创新团队资助项目(2018CXTD07)

吴梦雪(1987−)，女，四川乐山人，副教授，博士，从事风—车—桥耦合振动研究；E−mail：mx_swpu@126.com

(编辑 蒋学东)