考虑追踪运行的高速磁浮辅助停车区设置优化

姜西，虞翊，邓志翔，林辉，陈光，邹海平

考虑追踪运行的高速磁浮辅助停车区设置优化

姜西1，虞翊2，邓志翔1，林辉2，陈光1，邹海平1

(1. 中铁第四勘察设计院集团有限公司，湖北 武汉 430063；2. 同济大学 国家磁浮交通工程技术研究中心，上海 201804)

以降低常导高速磁浮交通系统辅助停车区的建设成本为目标，根据磁浮列车与传统轮轨交通在运营方式上相类似的特性，分析辅助停车区对磁浮列车追踪运行的影响。在既有辅助停车区设置方法研究的基础上，考虑列车运行追踪间隔要求的运营场景，进而构建满足目标约束下的辅助停车区设置模型，给出一种辅助停车区设置优化调整的设置方法。针对该方法在一定运行场景下进行仿真计算，计算结果表明该方法能在列车连续安全运行要求和列车追踪间隔需求的双重约束下，使辅助停车区数量达到最小值，从而实现降低建设成本的目标。

高速磁浮；辅助停车区；列车追踪间隔；仿真计算

高速磁浮交通可适用于中长距离、大运量快速的客运交通，且具备节能环保、噪声低、爬坡能力强等优点[1−2]，其发展对完善我国高速客运交通网具有重大的技术和经济意义，有利于进一步增强我国核心竞争力，我国目前正在深入进行高速磁浮交通系统综合试验、集成验证、工程化应用等研 究[3−4]。辅助停车区作为当前条件下实现常导高速磁浮列车双限速安全防护的必要技术手段，是列车运营的基础设施之一[5]。研究辅助停车区的布置问题对于提高高速磁浮交通系统的通过能力、保证列车运行安全及减少建设经济成本等有着重要的意义。张振江等[6]根据磁浮列车的不同运行场景，提出了列车追踪间隔的动态调整策略和速度防护模型，并通过仿真说明了该模型能在一定程度上提高追踪运行的列车间的空间间隔。郑伟[7]介绍了磁浮列车多分区多车追踪运行的最优原则，分析了两站之间双线多分区的多列磁浮列车同向循环追踪运行模型，给出了相应的追踪运行最大和最小间隔时间算法，并利用仿真验证了算法的正确性。赖晴鹰等[8−9]考虑了辅助停车区对列车运行速度的约束，针对常导高速磁浮双限速防护的特点，提出了不同的适用于中高速磁浮列车节能速度曲线优化的算法。LAI等[10]以获取足够大的列车运行速度范围为目标，建立了设置辅助停车目标的优化调整模型，通过仿真计算说明该方法在一定的条件下能优化了辅助停车区的设置。这些研究为磁浮长大干线中多分区多车追踪运行场景提供了理论基础，对优化运营具有较重要的意义，但没有从设计角度考虑辅助停车位置对磁浮列车追踪运行的限制问题。虞翊等[11]提出了基于安全防护速度曲线的辅助停车区设置方法，并考虑了多目标速度曲线并存的线路上磁浮列车安全连续运行的情况，给出了相应的辅助停车区设置调整方法。本文在文献[11]研究的基础上，考虑了运输组织对列车追踪运行的需求，从设计的角度对辅助停车区设置调整优化展开了分析研究。

1 辅助停车区设置的影响因素与目标

1.1 辅助停车区设置的影响因素

辅助停车区的设置一般满足低速区相对密集、高速区相对稀疏的规律，其影响因素很多，根据对列车运行动力学基础[12]、运行控制系统对列车安全运行的要求及运营组织的需求分析可知这些因素主要包括：

1) 列车的运行速度；

2) 列车类型；

3) 车辆制动能力；

4) 线路的具体条件；

5) 滑橇和线路轨道面之间的摩擦系数；

6) 气候条件(风速)；

7) 运行控制系统的反应时间；

8) 定位系统的误差；

9) 列车运行组织模式的要求。

从运行控制系统安全性层面考虑，列车正常运行时，能连续安全的步进；在故障时，切断牵引后能利用惯性或涡流制动等措施安全地停靠至当前的目标停车区[5, 10]。从磁浮交通系统建设经济性层面考虑，在满足运行控制系统安全步进控制要求的基础上尽可能少的设置辅助停车区。从运营效率层面考虑，则要求辅助停车区的设置应能满足运输组织对列车作业和追踪运行的需求。

1.2 辅助停车区设置的目标

设两站之间的线路上有个辅助停车区，记车站和车站的位置范围为[S1,S2]和[S1,S2]、辅助停车区的位置为[S,S+]，其中S表示停车区的可达点位置、表示停车区的长度、S2＞S1＞S2＞S1。如图1所示，基于辅助停车区+1(当=+1时，该停车区为目标站)的可达点作列车最小速度曲线，交列车牵引的目标运行速度曲线于位置速度点P+1(s+1,v+1)，基于辅助停车区(当=0时，该停车区为起点站)危险点作列车最大速度曲线，交列车牵引的目标运行速度曲线于位置速度点P(s,v)。文献[11]给出的方法以全线辅助停车区数量达到最小值为目标，约束条件为列车可以连续安全的运行。其目标函数为式(1)，约束条件等效于式(2)。

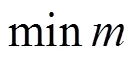
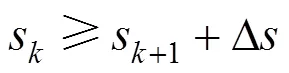
式中：Δ为能满足列车步进条件的最小距离要求。

本研究仍以辅助停车区数量最小为目标，同时考虑到列车连续安全运行和列车追踪运行对效率要求的双重约束条件。

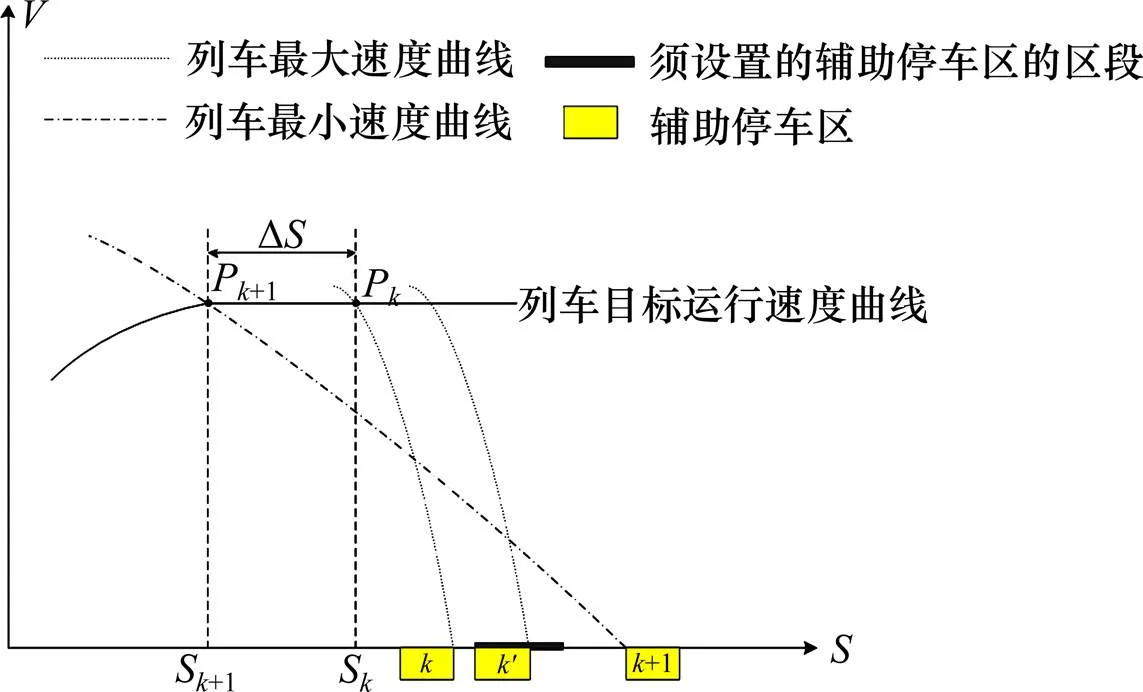
图1 辅助停车区位置计算过程

2 辅助停车区对列车追踪运行间隔的影响分析

2.1 追踪运行间隔情景

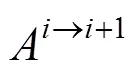
图2 辅助停车区分布

高速磁浮列车的追踪运行与普通轮轨列车的准移动闭塞追踪运行类似。不同的是，磁浮列车的移动授权只能是到停车区的且从安全的角度考虑列车一般情况下只能停到辅助停车区，而轮轨列车的移动授权是到分区边界的而列车可以停在闭塞分区的任意位置[10−11]。因此高速磁浮列车的运行追踪间隔受辅助停车区位置影响。同轮轨列车追踪运行类似，磁浮列车追踪间隔时间是指列车追踪运行时后续列车运行至前行列车当前位置所需的最小时间间隔[13−14]，追踪间隔时间t可用式(3)表述：

式中：t为列车发车追踪间隔；t为列车区间追踪间隔；t为列车到站追踪间隔。

2.2 列车发车追踪间隔

列车发车追踪间隔如图3所示。列车在分区1运行时，列车不能以分区1中的停车区为步进点运行。所以只有列车离开分区1后，列车b才能开始作业运行。列车恰好进入分区2时，列车开始进行发车作业，从列车发车作业开始至列车当前位置的时间即为发车追踪间隔时间t，加入系统延时的t可用式(4)表述：

式中：tw为列车发车作业的准备时间；Lo为列车在车站O停车点至分区车站边界的距离；L1为分区1的长度；Lv为列车车长；为列车的平均运行速度；tr为系统延时(含定位信息处理与传输延时、预排进路时间、分区切换启动时间等延时)。

2.3 列车区间追踪间隔

由A站发往B站的列车区间追踪间隔时间t可用式(6)表示：

2.4 列车到站追踪间隔

式中：Lw为接车站完成接车作业准备期间列车运行的距离；为辅助停车区的危险点至分区边界的保护区段长度；LD为分区n与车站D边界至列车停车点间的距离。

显然，列车的制动点与辅助停车区位置相关，即辅助停车区位置会影响列车追踪间隔时间。

3 考虑追踪间隔要求的辅助停车区设置优化方法

3.1 模型简述

根据上海高速磁浮商业示范运营线和传统轮轨交通系统的运营实际可知，为满足运输组织的需求，列车追踪运行的时间间隔必须达到行车组织的要求，若设追踪间隔要求为，则列车追踪运行对效率要求应满足式(8)的约束条件。

结合本文第2节的内容分析可知，式(8)等效于式(9)。

式中：l为必要的保护区段长度。

因为辅助停车区数量最小等效于两两辅助停车区之间间距最大，故目标函数式(1)，等效于式(11)。

即设置辅助停车区时可以式(11)为目标，需同时满足式(2)和式(10)的约束。

3.2 辅助停车区设置优化方法

图6 必要的辅助停车区分布示意

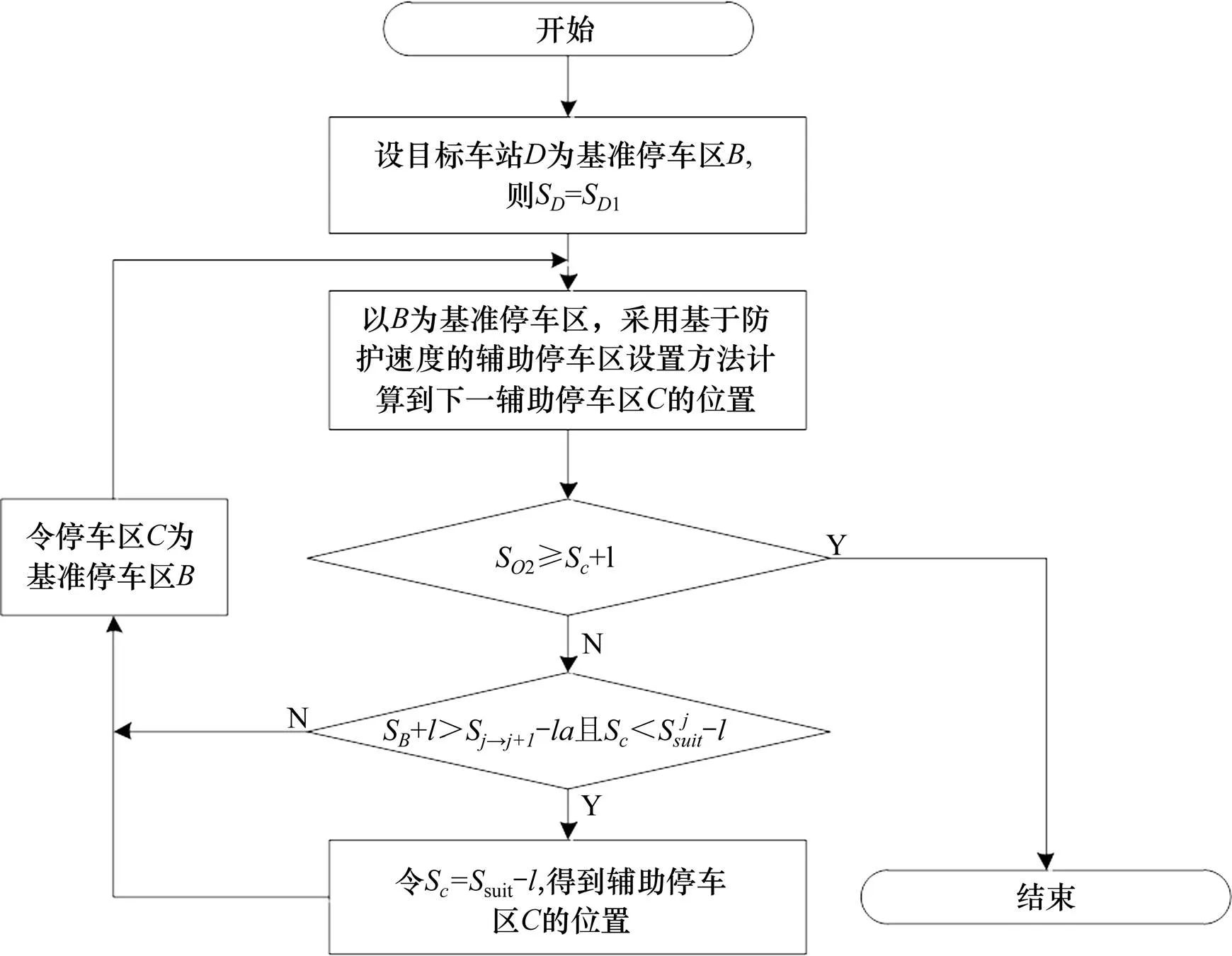
图7 辅助停车区优化调整流程

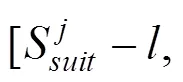
4 算例分析

4.1 基础数据

仿真线路自起点站中心里程(位置为0)至目标站中心里程(位置为85 730 m)，全长85 730 m。其中，车站动力轨(包含加速区)终点位置为1 000 m处，车站动力轨起点位置为84 730 m处，线路纵坡坡道数据参见表1。

仿真线路分区位置数据信息参见表2。

表1 仿真线路纵坡坡道数据

表2 仿真线路分区位置

假定全线运行最大限速为500 km/h，列车实际运行最大速度为450 km/h。在考虑可能存在限速等情况下，列车目标运行速度曲线如图8所示。

图8 列车目标运行速度曲线

列车车辆设为3节编组列车，辅助停车区长度：车长+250 m。考虑到实际工程应用中列车运行控制系统存在的误差和步进控制的冗余时间，使用[11]中辅助停车区设置的工程计算模型，采用最大、最小速度曲线代替基本计算方法的安全制动和安全悬浮速度曲线的改进算法对辅助停车区进行计算，设步进控制过程在Δ=10 s内完成。列车牵引切断命令发出至牵引切断完成过程延时时长设为2 s，安全制动过程中牵引切断完成至涡流制动完全启用过程延时时长设为0.7 s；最不利条件下定位测速系统的定位误差设为2 m、测速误差为0.2 m/s。外界最不利情况下由站至站顺风风速为25 m/s，逆风风速为10 m/s，动摩擦因数最大值为0.25，最小值为0.1。安全制动过程中最不利加速度为2.68 m/s2，安全悬浮过程中最不利加速度为0.6 m/s2。假定运输组织的需求要求列车追踪间隔为=6 min，列车区间追踪运行过程中辅助停车区至分区边界的必要的保护区段长度至少为100 m。根据第2节中磁浮列车追踪间隔的分析可计算得到以目标运行速度曲线运行时，为满足运输需求而必须设置的辅助停车区的区段范围数据参见表3。

表3 必须设置辅助停车区的区段位置

4.2 算例结果与分析

不考虑磁浮列车运行效率，仅以全线辅助停车区数量达到最小值为目标，采用基础的基于防护速度计算辅助停车区的方法可得仿真线路中辅助停车区的分布情况如图9所示，辅助停车区具体位置数据参见表4。

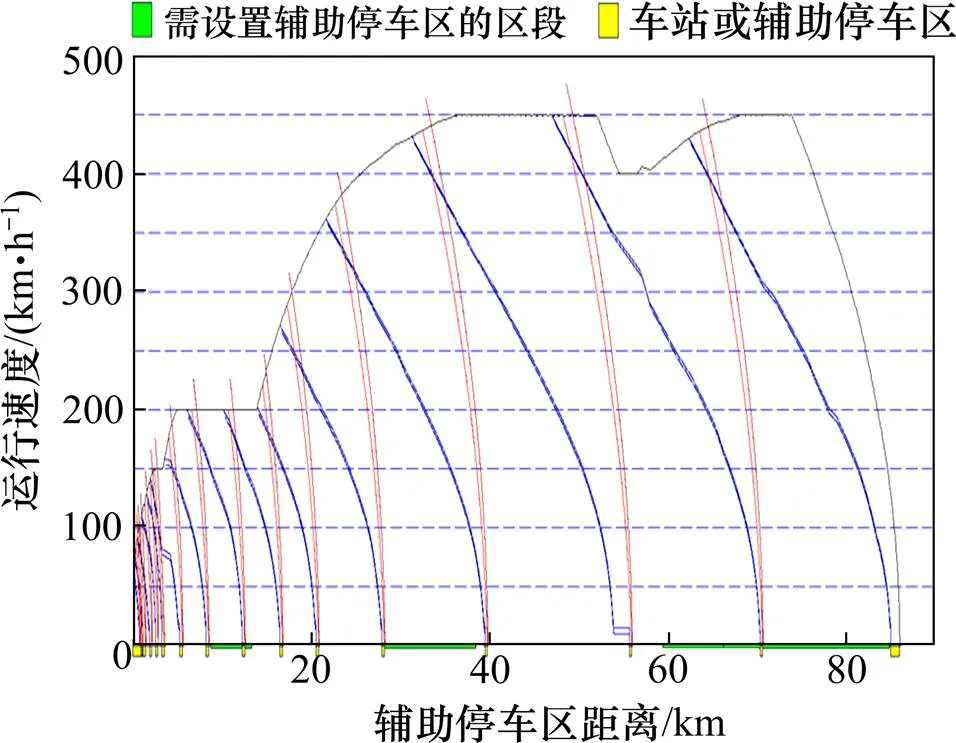
图9 基础的辅助停车区位置分布

采用基于防护速度的计算方法达到使辅助停车区数量最小的目标，但显然在区段[59 319,66 138]上无辅助停车区，不能满足列车追踪运行间隔的要求。在考虑运营效率的条件下，为满足运输组织的需求，列车追踪运行的时间间隔必须达到行车组织的要求，根据本文第3节介绍的计算方法得到仿真线路中辅助停车区的分布情况如图10所示，辅助停车区具体位置数据参见表5。

表4 基础的辅助停车区位置数据

图10 考虑追踪间隔的辅助停车区位置分布

算例中，基于防护速度计算辅助停车区的基本方法计算得到的辅助停车区数为14个，采用直接插值的方法需在区段[27 908, 38 405]，[59 319, 66 138]上各加入一个辅助停车区，以满足列车追踪间隔的要求，此时辅助停车区数量调整为16个。优化调整的考虑磁浮列车追踪运行间隔要求的算法得到的辅助停车区数为14个。计算结果表明，调整后的算法对辅助停车区数量影响很小，能满足加入的追踪间隔时间约束，优于采用直接插值计算的方法。考虑追踪间隔要求的辅助停车区设置优化方法更符合运营实际对效率要求的场景，并可在此约束下使全线辅助停车区总数最小。

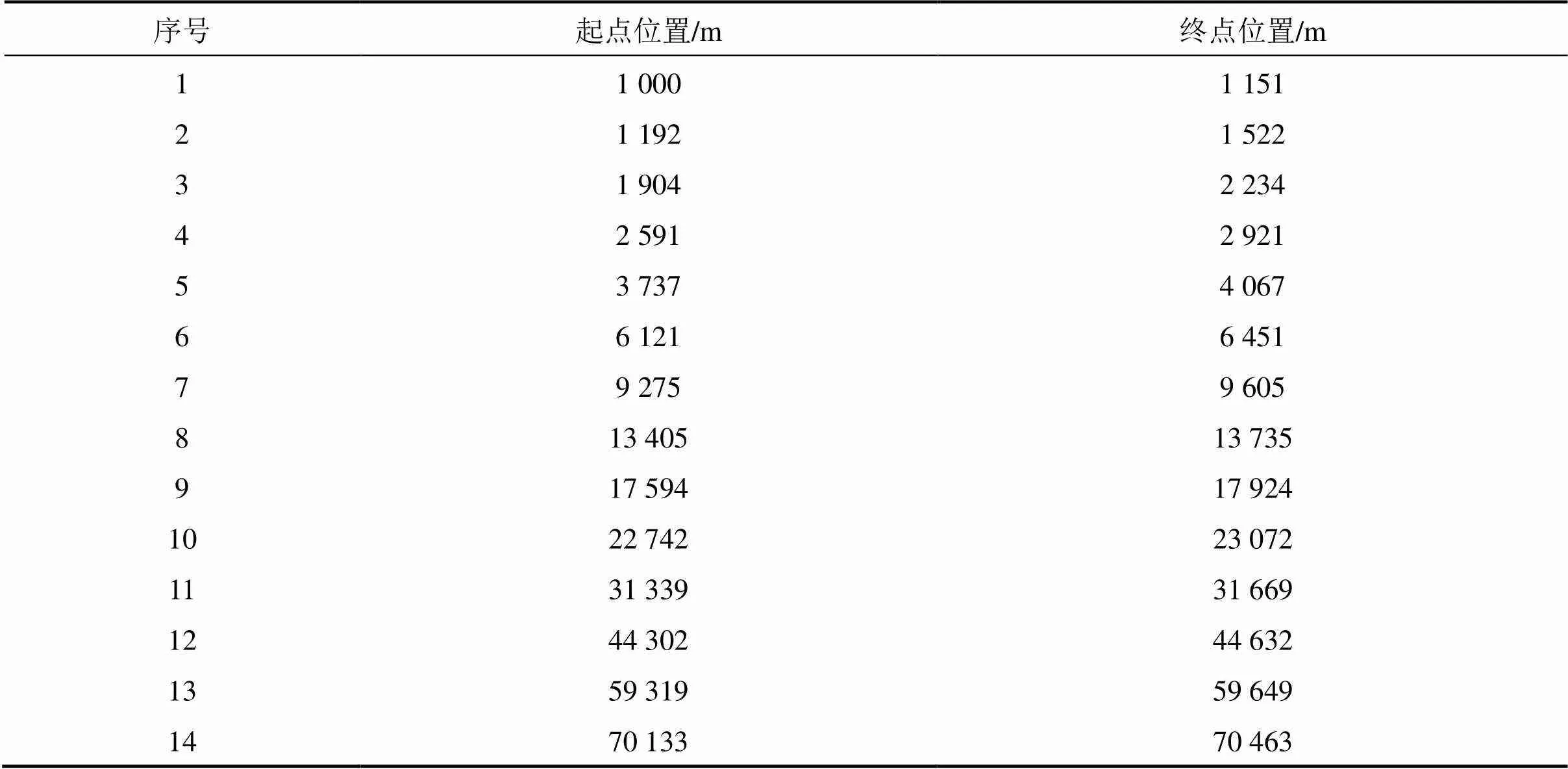
表5 考虑追踪间隔的辅助停车区位置数据

5 结论

1) 参考传统轨道交通和上海高速磁浮商业示范线运营经验，分析了常导高速磁浮交通系统列车追踪运行受辅助停车区影响的特点。

2) 基于防护速度计算辅助停车区的基本方法，考虑了列车追踪运行的场景，提出了更贴合运营实际需求的辅助停车区布置的方法。

3) 通过在一定工况下的仿真计算，说明了该方法可计算得到满足列车追踪间隔要求的辅助停车区且停车区数可达到最小值。可为将来的常导高速磁浮辅助停车区位置设计提供依据。

[1] YAN Luguang. Progress of high-speed Maglev in China [J]. IEEE Transactions on Applied Superconductivity, 2002, 12(1): 944−947.

[2] Lee H W, Kim K C, JU L. Review of Maglev train technologies[J]. IEEE Transactions on Magnetics, 2006, 42(7): 1917−1925.

[3] 朱忠英. 磁浮交通运营安全保障体系研究[J]. 科技资讯, 2017, 15(1): 43−44, 46. ZHU Zhongying. Research on the safety guarantee system of maglev transportation operation[J]. Science and Technology Information, 2017, 15(1): 43−44, 46.

[4] LIN G, SHENG X. Application and further development of Maglev transportation in China[J]. Transportation Systems and Technology, 2018, 4(3): 36−43.

[5] 吴祥明. 磁浮列车[M]. 上海: 上海科学技术出版社, 2003. WU Xiangming. Maglev train[M]. Shanghai: Shanghai Science and Technology Press, 2003.

[6] 张振江, 刘云, 冯玉珉. 磁悬浮列车追踪模型的研究与仿真[J]. 系统仿真学报, 2006, 18(4): 841−846. ZHANG Zhenjiang, LIU Yun, FENG Yumin. Study and simulation of Maglev railway tracing model[J]. Journal of System Simulation, 2006, 18(4): 841−846.

[7] 郑伟. 高速磁浮列车多分区追踪算法研究[J]. 计算机仿真, 2009, 26(9): 239−242. ZHENG Wei. A multi-decentralization tracking algorithm for high-speed Maglev train[J]. Computer Simulation, 2009, 26(9): 239−242.

[8] 赖晴鹰, 刘军, 赵若愚, 等. 基于变间距动态规划的中高速磁悬浮列车速度曲线优化[J]. 吉林大学学报(工学版), 2019, 203(3): 749−756. LAI Qingying, LIU Jun, ZHAO Ruoyu, et al. Optimal trajectory planning for middle-to-high speed maglev based on dynamic programming with mutative spacing[J]. Journal of Jilin University (Engineering Science Edition), 2019, 203(3): 749−756.

[9] 柴晓凤, 刘军, 赖晴鹰, 等. 考虑辅助停车区约束的中速磁浮列车速度曲线节能优化方法[J]. 中南大学学报(自然科学版), 2019, 50(6): 1499−1506. CHAI Xiaofeng, LIU Jun, LAI Qingying, et al. Optimal energy-efficient trajectory planning for middle-speed maglev considering constraint of auxiliary stopping area [J]. Journal of Central South University (Natural Science), 2019, 50(6): 1499−1506.

[10] LAI Q, LIU J, MENG L, et al. Optimization of the auxiliary stopping area planning in the middle-to-high speed Maglev[J]. Transportation Systems and Technology, 2018, 4(2): 141−151.

[11] 虞翊, 姜西, 林辉, 等. 基于防护速度的高速磁浮辅助停车区设置[J]. 同济大学学报(自然科学版), 2019, 47(9): 1310−1316. YU Yi, JIANG Xi, LIN Hui, et al. Research on setting method of auxiliary stopping area for high-speed Maglev based on protection speed curve[J]. Journal of Tongji University (Natural Science Edition), 2019, 47(9): 1310− 1316.

[12] 赖纳·沙赫, 彼得·耶勒, 勒内·瑙曼. 高速磁浮与高速轮轨交通系统比较[M]. 北京: 中国科学技术出版社, 2008. Schach R, Jehle P, Naumann R. Comparison of high-speed maglev and high-speed wheel-rail transportation systems[M]. Beijing: China Science and Technology Press, 2008.

[13] WANG N, TANG Y, LIU X. Calculation method on tracking interval of magnetic levitation train[C]// 2018 11th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 2018: 332−336.

[14] 侯黎明, 孙鹏飞, 聂英杰, 等. 高速铁路追踪间隔分析与优化设计研究[J]. 铁道运输与经济, 2018, 40(6): 5− 11. HOU Liming, SUN Pengfei, NIE Yingjie, et al. A study on optimizing high-speed railway tracking intervals[J]. Railway Transport and Economy, 2018, 40(6): 5−11.

Setting optimization of auxiliary stopping area for high-speed maglev considering train tracking operation

JIANG Xi1, YU Yi2, DENG Zhixiang1, LIN Hui2, CHEN Guang1, ZOU Haiping1

(1. China Railway Siyuan Survey and Design Group Co., Ltd., Wuhan 430063, China;2. The Cooperative Center of Rail and Maglev Transit, Tongji University, Shanghai 201804, China)

With the goal of reducing the construction cost of the auxiliary stopping area of the high-speed maglev transportation system，the impact of the auxiliary stopping area on the maglev train tracking operation is analyzed according to the similar characteristics of the operation mode of maglev trains and traditional wheel-rail transportation. An auxiliary stopping area setting model, which has considered the objective constraints and the operation scenarios required by intervals of trains, is constructed based on the existing research. And a setting method for the optimal adjustment of the auxiliary stopping area setting is proposed. The method is simulated in a certain operating scenario. The results show that the method can minimize the number of auxiliary stopping areas under the dual constraints of safe-continuous operation and the requirement of intervals of trains, then the goal of reducing costs is achieved.

high-speed maglev, auxiliary stopping area, intervals of trains, simulation calculation

U237

A

1672 − 7029(2021)02 − 0325 − 09

10.19713/j.cnki.43−1423/u.T20200324

2020−04−18

中铁第四勘察设计院集团有限公司重大课题(2019K131)；“十三五”国家重点研发计划资助项目(2016YFB1200602-02)

虞翊(1962−)，男，江苏无锡人，研究员，从事轨道交通信号安全与控制研究工作；E−mail：12164@tongji.edu.cn

(编辑 蒋学东)