“数形结合”思想在小学数学教学中的灵活应用

褚金花

(甘肃省武威市凉州区蔡庄小学 甘肃武威 733000)

《数学课程标准》指出，数形结合思想，其实质是将抽象的数学语言与直观的图形结合起来，利用数与形的相互转化来化抽象为直观，化难为易，相互依存，最大限度发展人的思维能力。在小学数学中这一思想虽未成形，但在教学中加以应用即可巧妙解决问题，又能拓展思维，对培养学生的数学素养，为以后解答数学问题，具有极大的帮助和促进作用。以小学数学中常见的六类问题的解答来领悟数形结合思想在解题中的奇妙之处。

一、在分数除法中的应用

在小学数学分数除法的教学中，开篇就有这样的问题。把一张纸的4/7 平均分成2 份，每份是这张纸的几分之几？刚开始接触这样的问题，学生无从下手，很难理解。在教学时利用数形结合思想，通过画图的方式，即可清楚明了地加以掌握。如下图所示：画一个长方形作为单位1，把它7 等分，其中的4 份即4/7 ，将这4 份涂上颜色（如图中黑色部分），再把黑色部分2 等份（用颜色深浅来区别），这时颜色较深部分即为题中所问，通过数长方形中的方格数即知答案为2/7。

二、倍数中的应用

在小学数学倍数的应用中，学生最难理解的是"倍"的概念，在一些应用题中，常把和倍问题综合在一起，难于理解，用图形演示来讲解此类问题是一种最简单又最有效的方法，便于学生理解并内化成自己的东西。

如：学校图书馆有文学类图书和军事类图书共1200 本，文学类图书的本数是军事类图书本数的3 倍。问两种图书各有多少本？

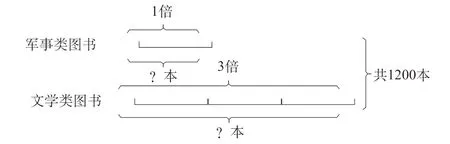
先画出图形，然后列式计算。

从图中可能看出，把军事类图书的本数作为1 倍数，文学类图书的本数就是它的3 倍，那么1200 本就相当于军事类图书本数的（1+3）倍，由此可先求出军事类图书的本数，再求出文学类图书的本数。

解：军事类图书的本数为：1200÷(1+3)=300 本

文学类图书的本数为：300×3=900 本

三、鸡兔同笼问题中的应用

例：笼子里有鸡和兔共若干只。从上面数有9 个头，从下面数有28 只脚，问鸡和兔各有几只？

关于这种问题的解答方法较多，但对于小学生来说，图示法最为直观简捷，通过这种解题方法来培养学生的数形结合思想，有助于培养学生的创新思维和数学意识。

如图所示，先画9 个○，表示鸡兔共有的9 个头；给每个头配上两只脚，共有18 只脚；然后再给每一个○添2 只脚，直到添至28 只脚为止。在图中便可数出有4 只脚的为兔，2 只脚的为鸡。

四、几何模型中的应用

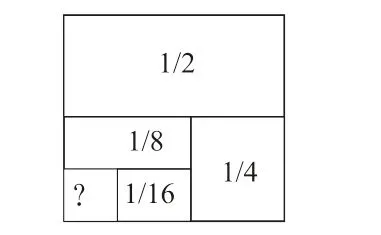
对于小学生来说由于逻辑推理有一定的难度，部分学生不容易明白，如果采用几何模型进行教学，学生都可轻松掌握。例如，计算“1-1/2-1/4-1/8-1/16 ＝”的问题。通过将上面的算式构造成下面的几何模型图，把一个大正方形看成单位“1”，一次又一次地进行平均分，从图上很容易看出1-1/2-1/4-1/8-1/16 ＝1/16。

五、正方形、长方形中的应用

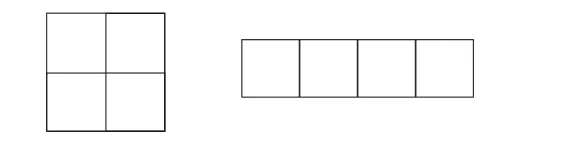
学完长方形和正方形的周长后，有一题是这样的：用4 个边长为3 厘米的正方形拼成一个长方形或正方形，周长最大是多少？最小是多少?

我给学生启示：先想有几种拼法?再想拼好后长和宽各是多少？在我的启发下，学生很快拼出了两种图形，然后根据图形进行计算，这样迅速、准确地做出了答案。

在这样的探究过程中，把“数形结合思想”有意识的渗透在获得知识和解决问题的过程中，充分利用直观图形，把抽象内容视觉化、具体化、形象化，化深奥为浅显。那么，学生所掌握的知识才是鲜活的，可迁移的，学生的数学素质才能得到质的飞跃[1-4]。

在小学数学教学中，数形结合能不失时机地为学生提供恰当的形象材料，可以将抽象的数量关系具体化，把无形的解题思路形象化，不仅有利于学生顺利高效地学好数学知识，更利于学生学习兴趣的培养及智力的开发，为学生今后的数学学习，甚至物理、化学等理科的学习打下坚实的基础。