浅谈小学数学习题的计算蕴含的矩阵运算算理

叶 敏

(重庆高新区康居西城小学校重庆 400000）

矩阵的研究历史悠久，与线性方程组、向量组一起组成了线性代数这门课程的主要知识点。最初，矩阵作为解决线性方程的工具被提出来，对于矩阵的概念理解为“数的矩形阵列”即矩阵的本质就是数阵。目前对于矩阵运算的实际应用分析成果较多，本文将一道小学数学试题的解答与矩阵的运算联系起来，从而进一步理解矩阵运算的本质和矩阵理论的内涵，有效地促进课程教学[1]。

例：某食品超市下设5 个分店，某日该超市向各店分配水果罐头，分别是芒果罐头、梨罐头、橘子罐头和苹果罐头，将配送个数汇总后，制作统计表如下：

分店罐头 1 2 3 4 5芒果 20 25 38 42 30梨14 20 10 31 25橘子 30 35 40 17 26苹果 25 30 22 27 36

表中数字可表示为如下4 行5 列的矩阵：

仍选用上述例子，第一天分配的罐头数不变，而罐头的价格和重量如下表：

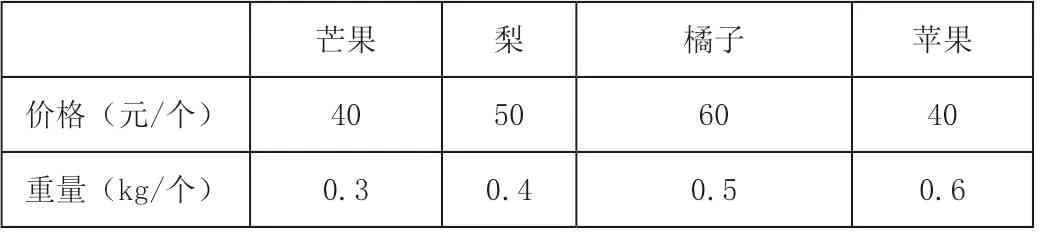
芒果 梨 橘子 苹果价格（元/个） 40 50 60 40重量（kg/个） 0.3 0.4 0.5 0.6

表中数据可表示为2 行4 列的矩阵如下：

若需要知道分配给各分店的罐头的总价和总重量，根据已有信息，可以利用代数的运算列式解决，第一天分配给各分店的罐头总价分别为

第一分店：40×20+50×14+60×30+40×25=4 300（元）

第二分店：40×25+50×20+60×35+40×30=5 300（元）

第三分店：40×38+50×10+60×40+40×22=5 300（元）

第四分店：40×42+50×31+60×17+40×27=5 330（元）

第五分店：40×30+50×25+60×26+40×36=5 450（元）

同理，可求出第一天每个分店分配的罐头总量。则总价和总量可表示如下：

1 2 3 4 5总价(元) 4300 5300 5300 5330 5450总量（kg） 41.6 51 48.6 49.7 53.6

于是，第一分店总价即为C 的第一行元素与A1的第一列元素分别相乘后相加，以此类推下去，就可以求出这五个分店的总价。同理，第一分店的罐头总量即为C 的第二行元素与A1的第一列元素分别相乘后相加，以此类推下去，可以得到超市第一天分配给每个店的总量，汇总后得到结果如上表所示。表中的数字可表示为2 行5 列的矩阵如下

根据运算，两个矩阵相乘，便有CA1=D。于是，矩阵乘法运算的一般表示为：

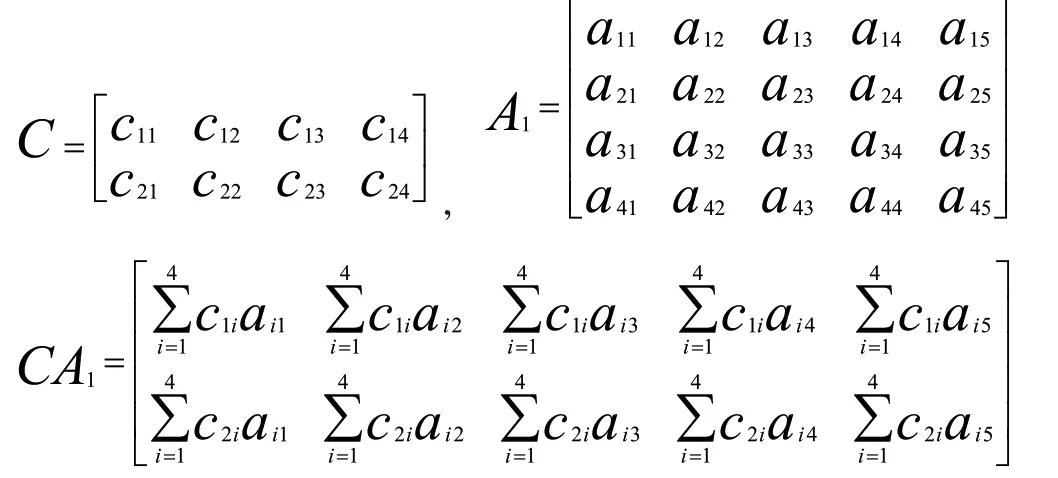
这样的乘法运算，其运算规则与普通数的乘法法则类似，但需要注意的是在进行矩阵乘法的运算时，相乘的左边一个的列数必须与右边的行数相同才能进行运算，所以矩阵的乘法不满足乘法交换律[2-4]。

通过以上的例子，在简单的情景中理解矩阵的运算方法，让复杂难懂的矩阵运算变得简单明了。而且矩阵作为高等代数一个非常重要的内容，其运算法则看似复杂难懂，如果能充分理解这些枯燥算式中所表示的丰富含义，让数学不仅仅是“源于生活”，更能“用于生活”，为生活服务，成为我们在生活中解决相关问题时的有效工具，在解决问题时起到事半功倍的效果。