非线性椭圆最优控制问题的谱方法研究

程 平

（华南师范大学 数学科学学院，广东 广州510631）

考虑如下非线性椭圆最优控制问题

这里的K 是个控制集合，即

1 最优性条件

状态方程标准的弱解形式描述如下

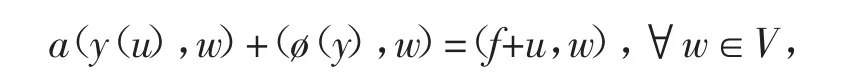
这里的（·，·）是L2（Ω）中的内积。因此非线性最优控制问题可以重述如下：寻找（y，u）满足如下条件

由文献［1］，我们知道最优控制问题至少有一个解（y，u），并且当且仅当存在一个共轭状态变量p满足最优性条件

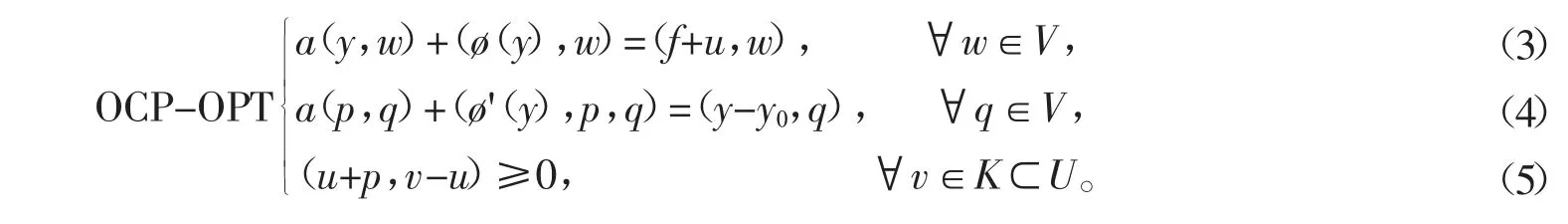
2 谱方法的离散格式

下面考虑用Galerkin 谱方法来做最优控制问题，假定Ω=（-1，1）2。首先考虑后面会用到的标准基函数。以xi（i=1，2）为变量，设定Lr（xi）为r 次的勒让德多项式，令

上述在离散空间中推出的最优性条件将在后面的误差估计中发挥重要作用。

3 控制变量与共轭状态变量的关系

因为控制约束集K=｛v∈L2（Ω）：Ω∫v≥0｝的特殊性，可以发现如果初始值是无限光滑的，那么最优控制问题的最优控制也可以无限光滑。

证明 这个证明和引理1 类似。

下面我们推出最优控制的正则性。

证明 由文献［1］，知道通过椭圆问题的一些结论可推得y∈H2（Ω），所以p∈H4（Ω）。由最优控制和共轭状态变量的关系

4 先验误差估计

借助辅助系统来考虑控制受限状态受限的非线性椭圆最优控制问题。定义J（·）和JN（·）如下

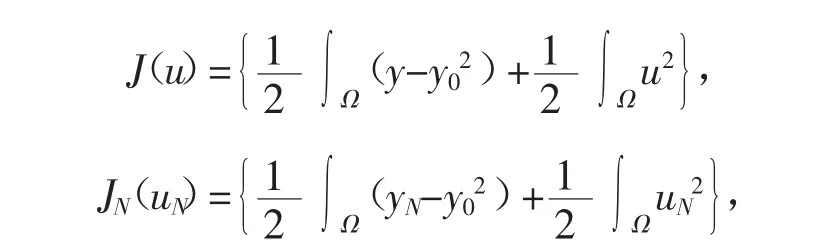
假定J（·）是一致凸的。所以这里存在一个与N 无关的c≥0，使得

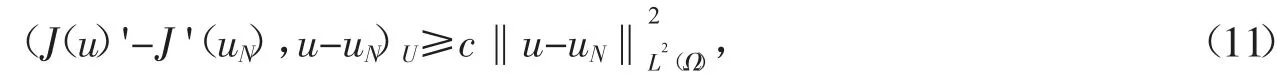
其中，u 和uN分别是式（3）～（5）和（8）～（10）的解。由文献［2］知

其中，p（uN）为下面辅助方程的解

定理1 令（y，p，u）和（yN，pN，uN）分别是式（3）～（5）和（8）～（10）的解。假定解（y，p，u）是足够光滑的，那么对任意的整数k＞0，存在与N 无关的C＞0，使得

证明 首先由前面假设的J（·）的一致凸性，以及式（12）～（14）和最优性条件（5），（10）以及施瓦茨不等式，对于任意的vN∈KN，有

由最优性条件（5），（10）知

所以对于不等式（18）右端的第1 项和第3 项可以进行放缩。对于第2 项因为

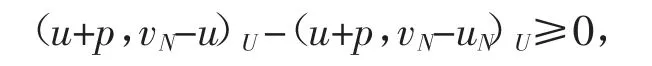
所以有

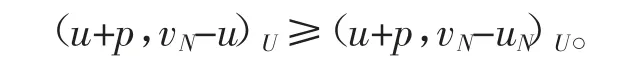
对于不等式（18）右端的第4 项有

综上可得

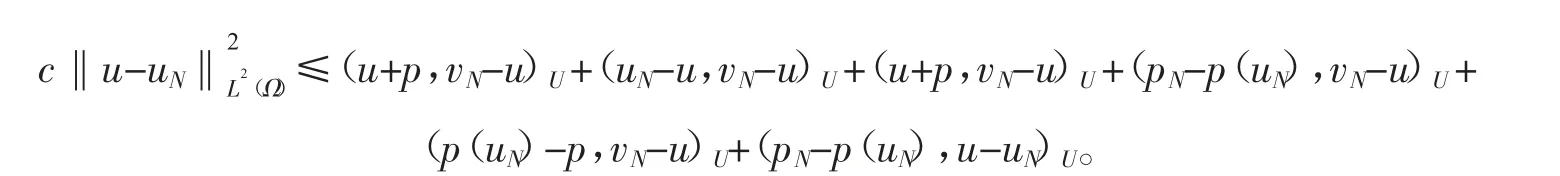
再利用施瓦茨不等式知

再由Young 不等式知

这里δ＞0 是一个足够小的常数。下面有不等式

由式（3）和（15）得到中间变量误差方程为

在上述方程里，设w=y（uN）-y，有

由于ø～'（y）≥0，可得

其中，c1=C（Ω）＞0 是下面庞加莱不等式的系数

所以

由式（8）和（15）得出

由式（22）可得

从而

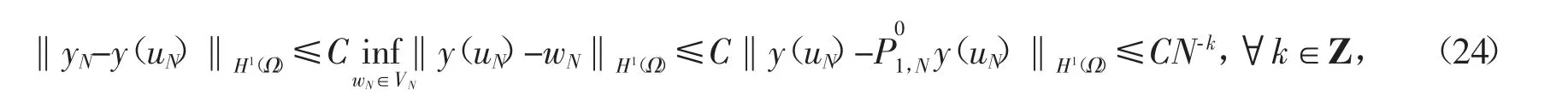
令q=p（uN）-P，则

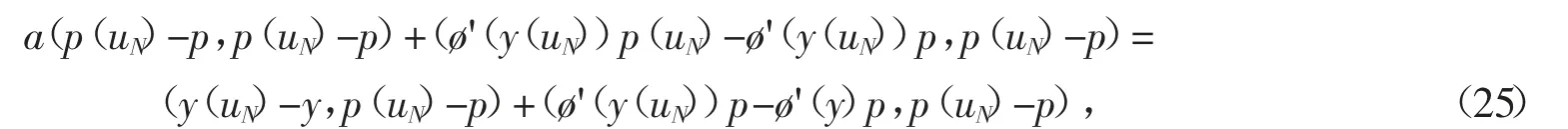
其中

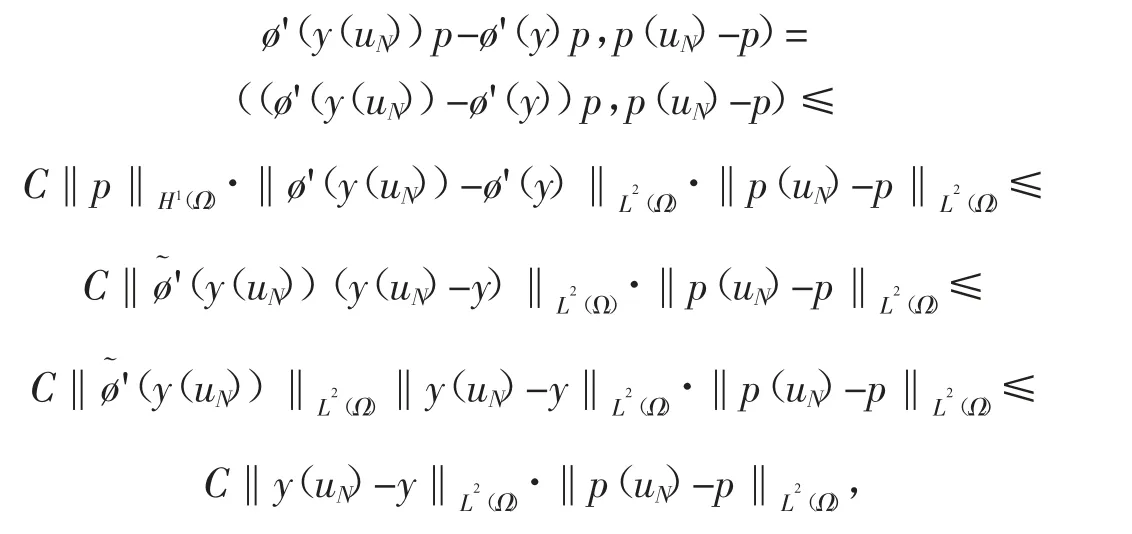
因此

再由式（9）和（16）得

将式（20）～（27）代入式（19）得

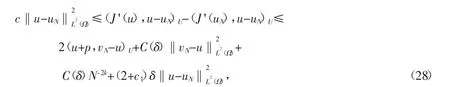
这里δ＞0 是一个足够小的常数。所以选择δ=c/（4-2c1）推出得

令上式中的vN=PNu∈UN，PN是L2正交投影算子，则

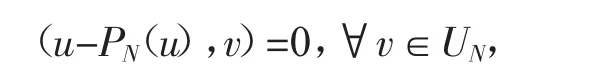
特别的，令v=1∈UN，则

因此

所以，vN∈KN⊂UN，由投影算子及其性质知

将式（30）运用到式（29）可以得到

最后结合式（20）～（28）和（31）可以得出误差估计（17）。