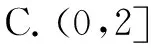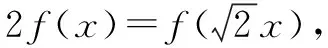全称量词与存在量词在高考中的运用

刘兆云

(江苏省宝应县安宜高级中学 225800)

全称量词与存在量词在最近的高考试题中频繁出现，量词作为一种工具显得越来越重要.下面我们一起看看在高考中以什么样的形式来考查“全称量词与存在量词”这一知识点.

一、量词在命题中的应用

例1(2009年普通高等学校招生全国统一考试(天津卷)数学(理工农医类))命题“存在x0∈R， 2x0≤0”的否定是( ).

A.不存在x0∈R, 2x0>0 B.存在x0∈R, 2x0≥0

C.对任意的x∈R, 2x≤0 D.对任意的x∈R, 2x>0

解析对含有一个量词的命题进行否定时，不仅要对量词进行否定，而且对后面的结论也要进行否定.本题“存在x0∈R”的否定是“任意的x∈R”，同时“2x0≤0”的否定是“2x>0”，故本题应该选择D.本题容易误选A，我们可以通过命题的真假来辨析，2x0>0 恒成立，即原命题：“存在x0∈R， 2x0≤0”是假命题；所以它的否定是真命题，而命题：“不存在x0∈R, 2x0>0”也是一个假命题.所以选项A是错误的.

评注含有一个量词的命题的否定形式：一般有下面两种情况：①“∀x∈M,p(x)”的否定为“∃x∈M,p(x)”;②“∃x∈M,p(x)” 的否定为“∀x∈M,p(x)”.

常用的正面词语与它的否定词语归纳如下：正面词语分别为：等于；大于；小于；是；都是；都不是；相应的否定词语分别是：不等于；不大于；不小于；不是；不都是；至少有一个是.正面词语分别为：至多有一；至少有一；任意的；所有的；至多有n个；任意两个；相应的否定词语分别是：至少有两个；一个也没有；存在的某些；至少有n+1个；某两个.

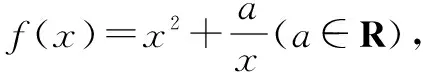
A．∀a∈R，f(x)在(0,+)上是增函数

B．∀a∈R，f(x)在(0,+)上是减函数

C．∃a∈R，f(x)是偶函数

D．∃a∈R，f(x)是奇函数

解析当a=0时，f(x)=x2是偶函数，即：∃a∈R，f(x)是偶函数，所以选择C.

例3 (2009年普通高等学校招生全国统一考试(宁夏卷)数学(理工农医类))有四个关于三角函数的命题：

p2: ∃x、y∈R, sin(x-y)=sinx-siny

其中假命题的是( ).

A.p1，p4B.p2，p4C.p1，p34.p2，p4

评注例2和例3都是要求理解“∀”和“∃”的含义；往往对于存在性问题只要找到一个满足题意的解即可；而对于任意性(恒成立)问题要说明它是真命题需要证明，而判断它是假命题时，只需要找到一个解说明原命题不正确就行.

二、量词在函数问题中的应用

例4 (2007年普通高等学校招生全国统一考试(安徽卷)数 学(理科))若对任意x∈R，不等式|x|≥ax恒成立，则实数a的取值范围是( ).

A．a<-1 B．|a|≤1 C．|a|<1 D．a≥1

解析对于含有绝对值的问题，不妨先考虑去掉绝对值.①当x>0时,∴x≥ax,即x(1-a)≥0,∴1≥a;②当x=0时,∴0≥0恒成立,此时a∈R;③当x<0时,∴-x≥ax,即x(1+a)≤0,a≥-1.由于对任意x∈R，不等式|x|≥ax恒成立，即|a|≤1.

评注分类讨论时需分清何时取并集、何时取交集、何时只能分开写.

例5 (2008年普通高等学校招生全国统一考试(天津卷)数学(文史类))设a>1，若对于任意的x∈[a，2a]，都有y∈[a,a2]满足方程logax+logay=3，这时a的取值的集合为( ).

A．{a|1

评注常见的全称量词是指：所有的、一切、任意一个、每一个、任给等；常见的存在性量词是指：存在一个、至少有一个、某个、有的、有些等.要搞清楚题目中到底是恒成立问题还是有解(存在性)问题.

例6 (2007年普通高等学校招生全国统一考试(天津卷)数学(文史类))设f(x)是定义在R上的奇函数，且当x≥0时，f(x)=x2，若对任意的x∈[t，t+2]，不等式f(x+t)≥2f(x)恒成立，则实数t的取值范围是( ).

评注在解决含有参数的不等关系时，常采用分离变量的方法，将条件转化为所求量与某个函数的不等关系.如:“tf(x)),若对于给定区间中的任意x原不等式恒成立，则t比f(x)的最小值小(t比f(x)的最大值大)就能保证原不等关系恒成立；而对于给定区间，则t比f(x)的最大值小(t比f(x)的最小值大)就能保证原不等式有解.