条件极值在中学数学中的应用研究

姚廷兰 王 杏

(1.贵州省贵阳市贵州民族大学 563000；2.贵州省遵义师范学院 563006)

王杏(1989.12-)，女，贵州省遵义人，讲师，从事工程数学研究.

基金项目贵州省科技合作计划项目《基于优化理论的点云模型特征提取算法的研究》(项目编号：黔科合LH字[2016]7030号)

一、条件极值简述

条件极值是指在一定的约束条件下求解最值问题，其中拉格朗日乘数法就是最常用的方法之一.对于许多较难证明的不等式问题，一般可转化为一定约束条件下求解最值问题，从而可以利用条件极值来解决不等式问题.下面介绍二元和n元的情况：

(1)用拉格朗日乘数法求解二元函数z=f(x,y)在约束条件φ(x,y)=0下的条件极值步骤如下：

作辅助函数

L(x,y,λ)=f(x,y)+λφ(x,y)

再令Lx=Ly=Lλ=0，即是

解上述方程组，可得到稳定点p0(x0,y0).

现需判断该稳定点是否为条件极值.如果是现实生活中的实际问题，由问题本身的性质进行判断；如果不是实际问题，可用二阶微分法判断.由此就可以把条件极值问题转化为讨论函数L(x,y,λ)=f(x,y)+λφ(x,y)的无条件极值问题.这种方法称为拉格朗日乘数法，函数L称为拉格朗日函数，辅助变量λ称为拉格朗日乘数.

作辅助函数

令LX1=LX2=…=LXn=Lλ1=Lλ2…Lλm=0，即

解方程组得到可能的条件极值点，再根据题目判定.

因此，若用求函数条件极值的拉格朗日乘数法来解决中学数学中一些较难的不等式证明问题，就较为容易理解，如中学数学选修4-5以及高考真题中的不等式问题.

二、条件极值在中学数学中的应用

1.在不等式问题中的应用

条件极值在不等式证明问题中的应用，先分析题目，需要找到约束条件和目标函数，进而转化为条件极值问题.通过构造辅助函数、求偏导、解方程组，

由此证明不等式.

例1(2019年全国Ⅱ卷)已知a,b,c为正数，且满足abc=1，证明：

(2)(a+b)3+(b+c)3+(c+a)3≥24

分析此题可看作在约束条件下求两个函数的最小值问题，进而用拉格朗日乘数法求解.

证明：(1)构造辅助函数L(a,b,c,λ)=a2+b2+c2+λ(abc-1)

解之，有a=b=c=1.

(2)构造辅助函数

L(a,b,c,λ)=(a+b)3+(b+c)3+(c+a)3+λ(abc-1)

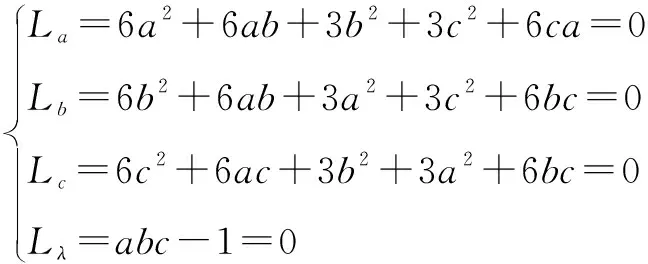
解之，有a=b=c=1.

考虑到在abc=1中，当a充分大时，(a+b)3+(b+c)3+(c+a)3的值可以充分大，从此题的实际出发，可推断当a=b=c=1时，函数(a+b)3+(b+c)3+(c+a)3的取得最小值24，所以有(a+b)3+(b+c)3+(c+a)3≥24.

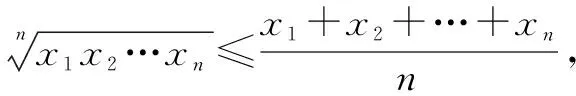
证明：设f(x1,x2,…,xn)=x1x2…xn，x1+x2+…+xn=m，用拉格朗日乘数法，构造辅助函数L(x1,x2,…,xn)=x1x2…xn+λ(x1+x2+…+xn-m)

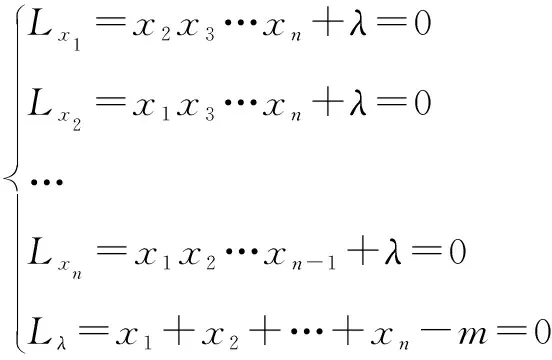
2.在函数问题中的应用

在实际的问题解决中，也涉及到不等式证明的问题.一般在有约束条件的情况下，可构造辅助函数，分别对变量进行求偏导，进而求解方程组，最后把结果代入目标函数中，即可证明.

例3农夫现需做一个容积为1立方米的圆木桶用于盛水，怎样设计此木桶才能使用料最少？

分析：此题可看作是一个条件极值问题，容积为1立方米就是一个约束条件，如何使用料最省，就是看表面积的大小，表面积越小，用料就越少.

解设圆木桶的底面半径为r,高为h，由题意可得容积V=πr2h=1，则表面积S=2πrh+2πr2.

构造辅助函数

F(r,h,λ)=2πrh+2πr2+λ(πr2h-1)

求偏导，得到

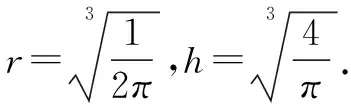
例4(1)求周长一定面积最大的矩形；(2)求面积一定周长最短的矩形.

分析这两个小题均是已知约束条件求最值问题，采用求偏导数，列方程组求解的方法.

解(1)设矩形的长为x,宽为y,则面积为S=xy(x>0,y>0).

约束条件为C=2x+2y

令L(x,y,λ)=xy+λ(2x+2y-C)

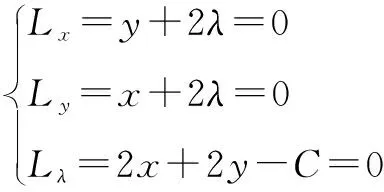
所以，在所有周长相同的矩形中，正方形的面积最大.

(2)设矩形的面积为S，约束条件为xy=S，

令L(x,y,λ)=2x+2y+λ(xy-S)

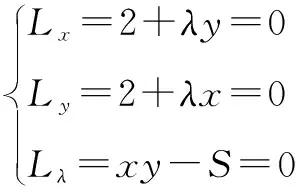
通过以上两个问题的求解，可知在遇到有约束条件问题时，也可选择用条件极值法求解，较简便，容易下手.

3.在三角函数证明问题中的应用

虽然条件极值在三角函数证明问题中的应用较为不是太多，但若题目满足条件极值法的条件时，也可通过找到约束条件和目标函数，然后构造辅助函数，求偏导，解方程组，从而解决问题.

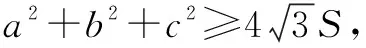
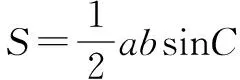
不等式问题贯穿于中学与大学中，应用非常广泛，而且还能开拓学生的思维能力，所以探究不同的方法解决不等式问题非常有必要.本文主要介绍了用《数学分析》中的条件极值法解决中学阶段的部分不等式问题，将不等式问题转化为条件极值问题，就可以利用条件极值法来解决不等式问题.实际上，利用多元函数的条件极值证明不等式，关键是选择适当的目标函数和相应的约束条件，这种证明方法对于证明含有多个变量的不等式问题是有效可行的，值得研究.