基于神经网络方法的对称矩阵特征值的求解
张 丽 丽
(陇东学院 数学与统计学院,甘肃 庆阳 745000)
矩阵的特征值问题作为矩阵理论中的一个重要内容,已被广泛应用于物理、化学、生物等多个研究领域。目前,矩阵特征值的计算方法主要有定义法[1]、幂法[2]、反幂法[3]和Jacobi方法[4]等。定义法对于较为复杂的矩阵其计算过程较为繁琐;幂法因迭代的局限性,其收敛性差较差;反幂法的计算精度虽然优于幂法,但要求特征值必须充分隔离;Jacobi方法需要借助MATLAB软件实现。1985年,Oja[5]等根据基础神经元网络模型提出了一种计算对称矩阵特征值的循环神经网络模型,基于此模型,1992年罗发龙[6]提出了一种用于最大似然(ML)方向估计的神经网络模型,但上述2种模型均只能计算矩阵的最大特征值及其对应的特征向量。2005年,刘怡光[7]等提出了一种求解矩阵一般特征值和特征向量的神经网络方法,但该方法计算量较大。此后,学者们相继提出了一些模型[8-10],如时滞标准神经网络模型(DSNNM)等,但这些模型收敛性均较差。为了进一步优化矩阵特征值的计算,本文在文献[5-10]的研究基础上提出了一种更为容易实现的计算一般对称矩阵特征值的神经网络模型。
1 求对称矩阵特征值的神经网络方法
人工神经网络(神经网络)是通过模仿生物大脑神经网络而建立的一种神经元模型,如图1所示,神经元处理信息的过程分为输入层、处理层、输出层3个层次。其中输入层相当于神经元的树突,处理层相当于神经元的细胞核,输出层相当于神经元的轴突。不同神经元之间的链接程度不同,其链接强度可用“权值”表示,记为Wi(i=1,2,…,n)。神经元对细胞核处理过程可看作是一个函数f(x)的计算过程,其中输入过程可看作自变量xi(i=1,2,…,n),输出过程可看作因变量yi(i=1,2,…,n)。
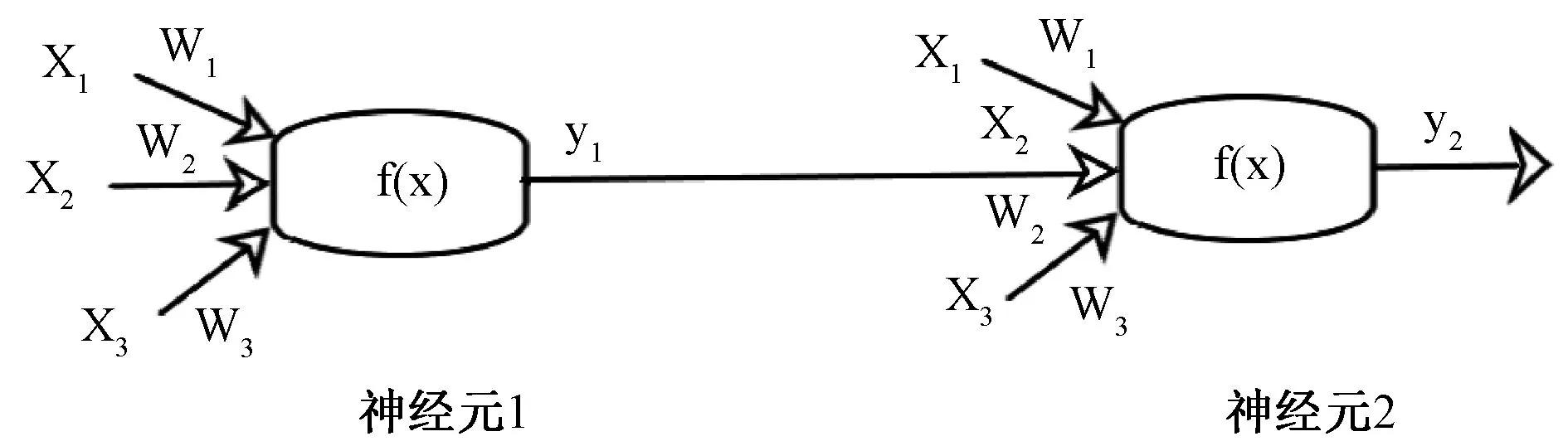
图1 神经元模型
根据图1,基础神经元模型可用下式表示
y1=f(W1x1)+f(W2x2)+…+f(Wnxn)
y2=f(f(W1x1)+f(W2x2)+…+f(Wnxn))+…+
f(f(W1x1)+f(W2x2)+…+f(Wnxn))
(1)
文献[5]根据上述基础神经元网络模型提出了如下循环神经网络模型
(2)
其中A为任意对称矩阵。基于此模型,文献[6]提出以下神经网络模型
(3)
将模型(1)代入模型(3)得
(4)
将(4)中的函数f(x)写成向量形式可得
(5)
但模型(2)-(5)只能计算矩阵的最大特征值及其特征向量。为此,本文引用一种连续型全反馈神经网络模型
(6)
其中X(0)为非零初始向量。
因上述模型均只能计算对称矩阵,因此本文只研究对称矩阵特征值的计算。设n阶实对称矩阵A,其特征值为λ1,λ2,…,λn,对应的特征向量为e1,e2,…,en。由于实矩阵的特征值均为实数,所以矩阵A至多有n个实特征值。由对称矩阵A可得如下定理:
定理1对称矩阵每个特征值重数等同于与其无关的特征向量数。
由定理1知n阶实对称矩阵A存在n个线性无关的特征向量,即对称矩阵一定可以对角化。再由矩阵对角化相关理论可知,存在可逆矩阵P,使得矩阵A可以对角化为矩阵V,即V=P-1AP(V=diag(λ1,λ2,…,λn))。设λi,λj是实对称矩阵A的两个特征值,其对应的特征向量为ei,ej,则存在如下关系
Aei=λiei
Aej=λjej
(7)

(8)
将(7)代入(8)得
由以上可得
(9)
因实对称矩阵A的任意两个特征向量两两正交,因此对于实对称矩阵A有
结合(9)式及模型(6)即可得到计算特征向量和特征值的如下关系
(10)
其中e0为非零初始向量。对于n阶实对称矩阵A
将矩阵A代入模型(6)得
(11)
对X(t)取非零初始向量X(0)=[a1na2n…ain0]T,i∈(1,n)则有
(12)
由(12)可得
(13)
将(13)代入(11)得
(14)
取垂直于初始向量X1(0)的初始向量X2(0)=「-a1n-a2n… -ainanm⎤T,然后将其重新代入模型(6)可得
(15)
重复式(12)—(14)的计算过程可得
(16)
取垂直于初始向量X1(0)、X2(0)的初始向量X3(0),并重复式(12)—(14)的计算过程即可得到特征向量e3和特征值λ3。继而取与之前初始向量垂直的初始向量按式(12)—(14)的计算过程反复计算,即得到给定对称矩阵的特征向量e1,e2,…,en和特征值λ1,λ2,…,λn。
2 斐波那契数列
斐波那契(Fibonacci)数列又称为“兔子数列”,是由数学家斐波那契在兔子繁殖过程中以兔子数量的变化提出的数学问题[11],即:设一对兔子每个月都能繁殖出一对兔子,假定所有兔子都没有死亡的情况,问第F个月后可以繁殖多少对兔子。
根据斐波那契数列有
{Fk}=0,1,2,3,5,…,Fk,…
(17)
其约束条件为
(18)
通过数列,可以推得幼崽对数、成兔对数与月份的关系,如表1所示。
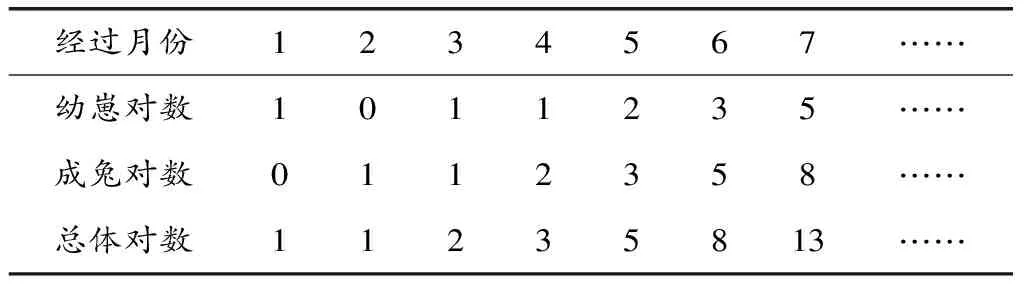
表1 幼崽对数、成兔对数与月份关系表
将表1的递进关系写成矩阵的形式,设矩阵A
即前后月的递进关系矩阵形式有
那么,∂k+1可表示为矩阵形式
(19)
其中k=1,2,3,…
为了计算∂k,将(19)式进行迭代
(20)
由此,将Fk与∂k联系起来,只需计算Ak即可。
将第k+1月初时的兔子总数设为X(k+1),则通过(20)式可知第k+1月初与第k月初时的兔子总数有着以下关系
X(k+1)=AX(k)=A2X(k-1)=A3X(k-2)
(21)
递推得到
X(k+1)=……=AkX(1)
(22)
前后月份写成矩阵形式的关系式有
(23)
由矩阵对角化的理论,只需要将A化成
A=PAP-1
(24)
的形式即可求出FK。
为了方便计算,由于矩阵A有n个线性无关的特征向量,所以假定存在一对角矩阵P,若P-1AP=A,则有P-1AKP=AK,从而
AK=PAP-1,K∈N
(25)
故矩阵A与矩阵P相似,即矩阵A可对角化。
设矩阵A的特征值为λ,E为单位矩阵,通过矩阵特征值定义可知
(26)
通过计算可得矩阵A的特征值
(27)
显然,对于矩阵A的两个特征值分别存在对应的特征向量X1,X2
X1=(λ11)T
X2=(λ21)T
(28)
假设
(29)
通过计算可得
(30)
通过计算可知矩阵A的特征值有两个,为了将矩阵A构造为对角矩阵,以两个特征值λ1,λ2为对角元素进行构造
(31)
由于(25)式,那么
由此可以得出
(32)
第k+1个月初兔子的对数为
(33)
又由(22)式通过矩阵特征值求出的斐波那契数列通项为
(34)

