双层最值问题的解法探秘

浙江省嘉善第二高级中学 (314100) 鲁和平

双层最值问题是指在一个最值问题中又包含一个最值问题.它大致可分为四大类：求最大值中的最小值；求最小值中的最大值；求最大值中的最大值；求最小值中的最小值.尤以前面两类问题居多.这类问题在高考模拟卷和竞赛卷中会经常出现，常以选择题或填空题的方式呈现.最值问题，历来就是高中数学的热点和难点问题，而双层最值更加大了最值问题的理解难度.因此，大部分学生见到此类问题都是望风披靡，视为若猛虎.其实，只要认真归纳总结，还是可以找出此类问题的一般解题规律的.

一、相乘策略

将已知问题转化为几个同向不等式，再将这几个不等式相乘，综合运用不等式相关知识即可求解.

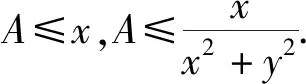
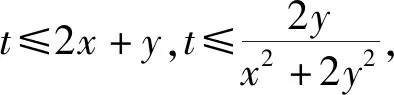
二、相加策略

根据已知条件，得出几个同向不等式，将这几个同向不等式相加，再以不等式知识综合求解

例3 对于任意实数a,b，不等式max{|a+b|, |a-b|,|2006-b|}≥c恒成立，则常数c的最大值是.

解：设M=max{|a+b|,|a-b|,|2006-b|} ，则M≥|a+b|,M≥|a-b|,M≥|2006-b|，从而4M≥|a+b|+|a-b|+2|2006-b|≥|(a+b)+(b-a)+2(2006-b)|=4012，所以M≥1003所以c≤1003，故常数c的最大值为1003.

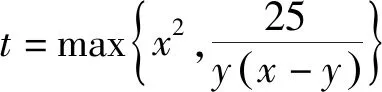
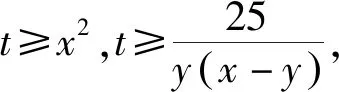
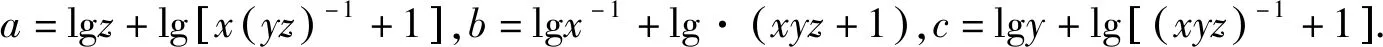
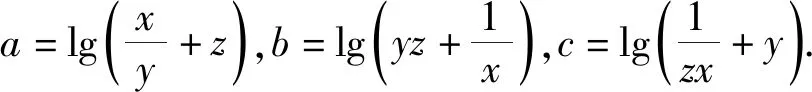
三、构造策略

将问题转化为若干个已知得不等式，对这几个不等式进行重组拓展，构造出新的不等式，解这个新的不等式即可求解.

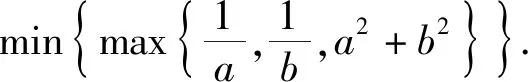
例8 设x>1,y>1，s=min{logx2,log2y,logy(8x2)}，则s的最大值为.(2006年陕西高中数学联赛题)

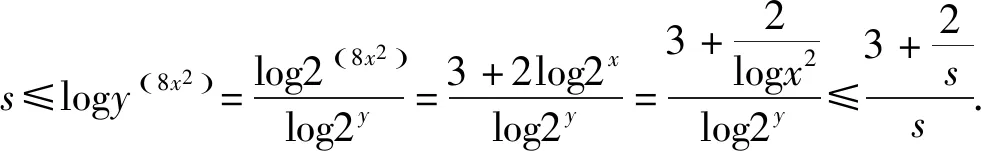
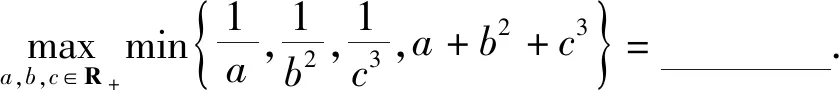
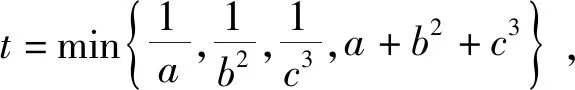
例10 已知a,b,c∈R+且a+b+c=12,ab+bc+ca=45,求minmax{a,b,c}.

解：不妨设a=max{a,b,c} ，由a+b+c=12可得12≤3a,即a≥4,则a≥b,a≥c⟹(a-b)(a-c)≥0⟹a2-(b+c)a+bc≥0⟹a2-(12-a)a+bc≥0⟹bc≥12a-2a2,又45=ab+bc+ca=bc+a(b+c)=bc+a(12-a)≥12a-2a2+a(12-a)⟹a2-8a+15≥0⟹a≥5,当且仅当a=b=5,c=2时，得minmax{a,b,c} =5.

例11 已知实数a,b,c满足a+b+c=0,abc=1,求minmax{a,b,c} 的值.

四、画图策略

运用数形结合思想，因数构形，以形助数.通过观察图形，找出最值中蕴含的最值.

图1

例12 对于每个实数x，设f(x)=min{4x+1,x+2,4-2x}，则f(x)的最大值是.