2020年高考北京卷解析几何试题的探究与推广*

广东省中山市濠头中学 (528437) 闫 伟 何 杰

圆锥曲线与直线的位置关系一直是高考的热点和难点，在很多圆锥曲线题目中都是探求一些特殊结论如定值问题，这些结论看似特殊，实则都具普遍性，且往往具有丰富的命题背景和深厚的内涵，研究此类试题不仅能够更好的把握解析几何的本质，还能透过试题挖掘隐含的命题规律，更能将其拓展到一般情况，从而提升学生数学思维，发展数学核心素养.下面以2020年高考北京卷解析几何试题为例进行说明.

1.试题呈现与分析

试题分析：本题主要考查椭圆的标准方程及其几何性质、直线与椭圆的位置关系、韦达定理、线段长度定值的证明等基础知识，能力层面突出考查学生的推理论证能力、运算求解能力以及综合运用所学知识分析问题和解决问题的能力，侧重考查数形结合、化归与转化的思想．试题分两问，梯度明显，既能让绝大多数考生有所收获，又能区分不同层次的学生，下面着重探讨第二问. 第二问要证明的线段BP和BQ的比值，解决思路是联立直线l与椭圆方程，利用M、N两点坐标分别表示两个线段长度，再结合韦达定理运算求解. 本题立意深刻、内涵丰富，具有一定的典型性、代表性，极具探究价值，是一道值得研究的好题．

2.试题解析

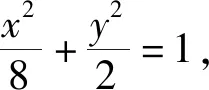
评注：本题要解决线段长度比值，先要用相关参数表示两个线段，再结合韦达定理进行化简求解，解题思路较为常规，只是运算量有些大，要求学生具备较高的数学运算、逻辑推理能力.

3.试题反思及GeoGebra平台的探究

实验:(1)在GeoGebra绘图区先设置两个“滑动条”a,b，输入x^2/a^2+y^2/b^2=1得到椭圆C；(2)在椭圆上任取点A(非短轴顶点)，并输入直线l:x=a^2/(x(A))且与x轴的交点为B；(3)过点B作与椭圆相交的直线，交点分别为M,N，再作出直线MA,NA以及与直线l的交点分别为P,Q；(4)拖动A点，或者直线MN，又或者改变参数a,b的值，进行演示，如图1、2.

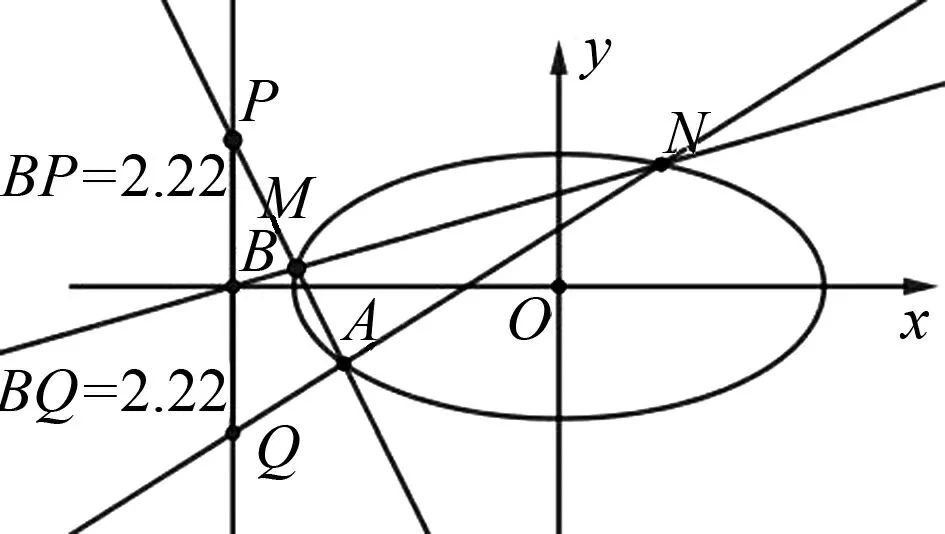
图1

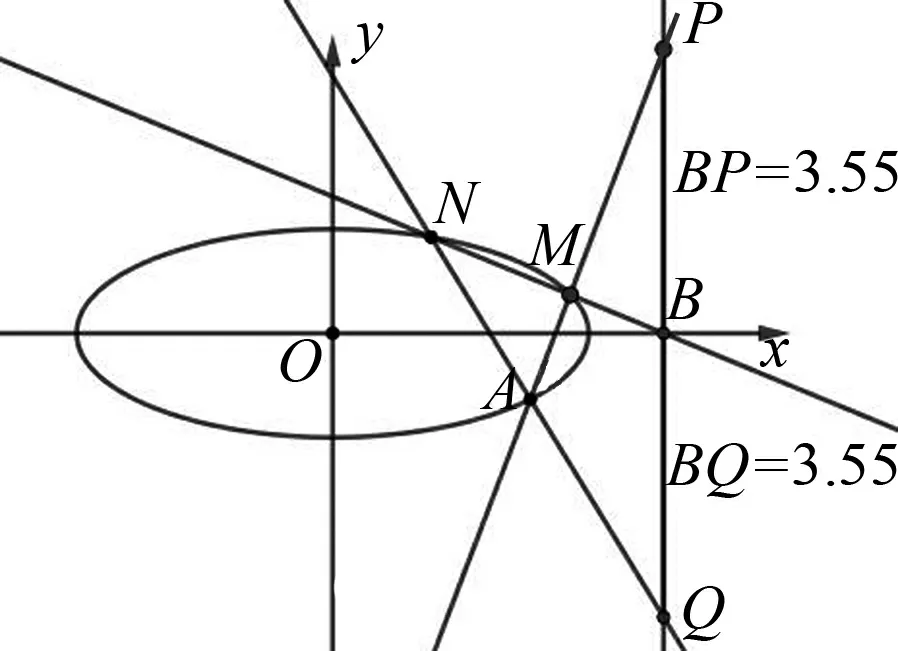
图2

通过实验演示进一步探究可知：只要满足A,B两点的横坐标乘积等于a2，即xA·xB=a2时，线段|BP|与|BQ|恒相等. 于是我们可以将试题结论推广到一般情形：

4 结论推广 揭示本质

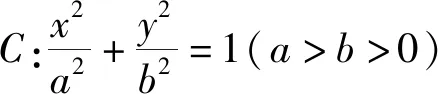
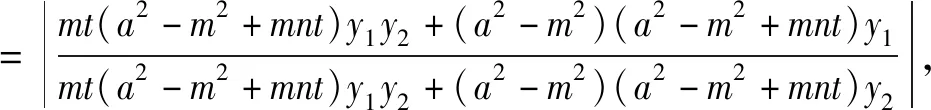
于是|BP|=|BQ|.

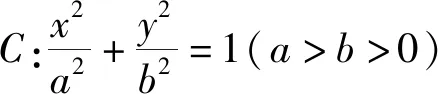
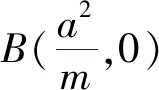
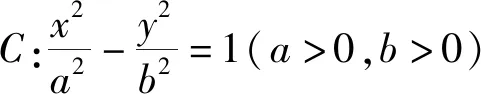
结论2、3、4的证明过程与结论1相仿，此处不一一赘述.对于抛物线，类似的我们有

结论5 已知抛物线C：y2=2px(p>0)过点A(m，n)(m≠0)，过点B(-m,0)的直线l交抛物线C于点M,N,直线MA,NA分别交直线x=-m于点P,Q，则|BP|=|BQ|.

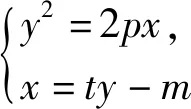
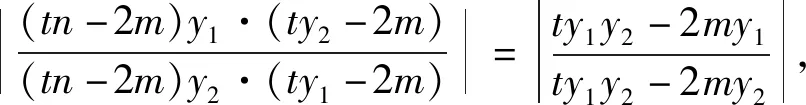
5 教学启示

数学教育家波利亚曾说：好问题同某种蘑菇有些相像，它们都成堆地生长，找到一个以后，你应当在周围找找，很可能附近就有好几个[1]. 高考试题是命题专家集体智慧的结晶，具有典型性和代表性，他们好比蘑菇，我们如果能以这些典型试题为出发点开展磨菇式的深入探究，便可以达到解法思路打通后讲一题，通一类,得一法的教学效果.

高考试题是命题专家的精心之作，每年的高考题在命题角度、题型难度等方面都进行了充分考量，除了具有测试与选拔功能外，还具有良好的教学功能，要了解高考动向、把握高考脉搏，高考试题的研究分析是重要的途径. 因而我们要对高考试题做深入的分析与探究，教师要跳入题海多做多思，才能做到融会贯通，帮助学生跳出题海. 对高考试题的深度研究，不仅能使我们精准地理解试题的背景和本质，还可以更好地培养学生思维品质，提高学生分析问题和解决问题的能力, 提升学生的数学核心素养.