探究一道数列递推问题的命制策略

江苏省海门中学 (226100) 徐巧石

笔者最近在高三复习中，遇到一道数列递推问题，很难处理，后来发现2017年就曾相遇，但没有及时思考总结，落笔成文，所以此次决定对其解法进行剖析与总结，同时进一步思考该题是如何命制的，还有哪些命制数列递推关系式的角度.

题目(2017届南通市二模·20)设数列{an}的前n项和为Sn(n∈N*)，且满足：①|a1|≠|a2|；②r(n-p)Sn+1=(n2+n)an+(n2-n-2)a1，其中r，p∈R，且r≠0． (1)求p的值；(2)数列{an}能否是等比数列？请说明理由；(3)求证：当r=2时，数列{an}是等差数列．

一、题之解

解：(1)n=1时，r(1-p)S2=2a1-2a1=0，因为|a1|≠|a2|，所以S2≠0，又r≠0，所以p=1．

(2)略；

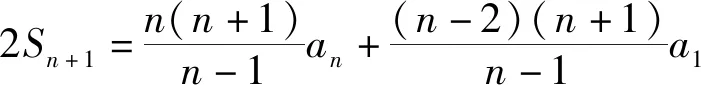
当n=3时，a4=3a3-3a2+a1⟺a4-2a3+a2=a3-2a2+a1=0，

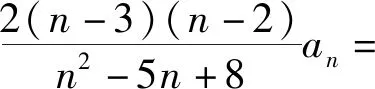
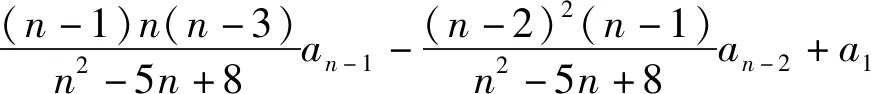
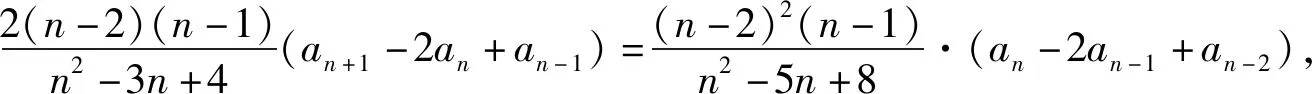
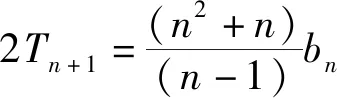
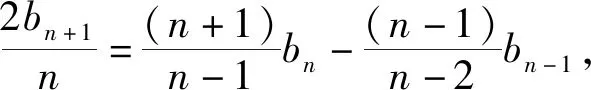
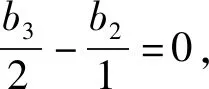
(思路2)2(n-1)bn+1=n(n+1)bn-n(n-1)bn-1①，当n=3时，b4=3(b3-b2)=2b3+b3-3b2=2b3-b2，所以b4+b2=2b3，当n≥4时，2(n-1)(n-2)bn=(n-1)nbn-1-(n-1)(n-2)bn-2②，①-②得2(n-1)(n-2)(bn+1-2bn+bn-1)=(n-1)·(n-2)(bn-2bn-1+bn-2)，又b4-2b3+b2=0，所以bn-2bn-1+bn-2=0，n≥4，又b3-2b2+b1=0，所以∀n≥3,bn-2bn-1+bn-2=0，所以{bn}是等差数列，所以{an}是等差数列.

反思：证明等差数列两种方法一是利用定义，即寻找相邻两项的关系；二是利用等差中项，即寻找相邻三项的关系.此题中第一步需要消去Sn+1，第二步的想法是将a1消去，直接作差相减需要减三次才可以将常数项a1消去，所以将a1前面的系数除去，直接一次相减便可以消去a1，从而得到相邻三项的关系式，若三项看不出，进而寻找相邻四项间的关系.递推关系处理等差(等比)数列问题的三种常见思路：(1)Sn与an之间的转化；(2)构造常数列过渡，得出通项，得到等差(等比)数列；(3)消递推关系中的常数，得相邻项关系．

二、题之思

上述递推关系式是如何构造的？命题者是从什么角度出发进行怎样命制的呢？

事实上，由d=d⟺nd=nd，利用通项公式隐藏公差d，因为nd=an+1-a1，nd=(an+1-an)，所以an+1-a1=n(an+1-an)⟺(n-1)an+1=nan-a1①，通过前n+1项和公式隐藏an+1，即先在①式两边同时加上(n-1)a1，再同时乘上n+1，即得(n-1)(n+1)(an+1+a1)=(n+1)nan+(n-2)(n+1)a1，即2(n-1)Sn+1=(n2+n)an+(n2-n-2)a1，上述每一步都是等价的转换的前提是{an}是等差数列，考虑其逆命题，证明{an}是等差数列.

三、题之究

还有哪些构造递推关系式证明等差、等比数列的方法呢？通过对相关问题的归纳总结，归结以下三种常用构造角度.

(一)由等差等比通项与前n项和公式构造

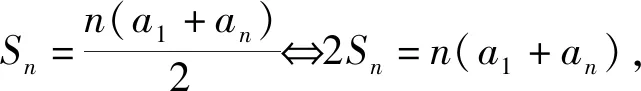
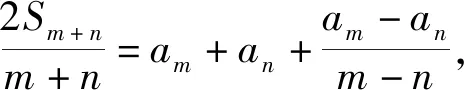
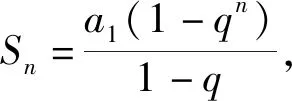
题2 已知各项互不相同的数列{an}，an≠0,n∈N*，前n项和为Sn，满足(an-an+1)Sn=(a1-an+1)an，求证：{an}是等比数列.

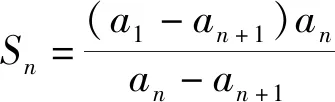
(二)由具体的数列通项与和公式构造

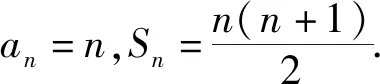
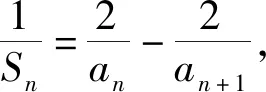
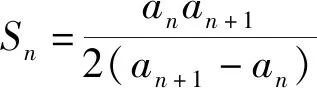
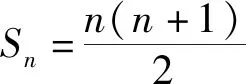
题4 已知数列{an}的前n项和为Sn，a1=1，a2=2,a3=3，且满足∀m,n，2Sm+n=S2m+S2n-(m-n)2，求数列{an}的通项公式.

解：令m=1得2Sn+1=S2+S2n-(1-n)2①，令m=2得2Sn+2=S4+S2n-(2-n)2②，②-①得2an+2=a3+a4-(2n-3)=a4+2n，令m=1,n=2得2(1+2+3)=(1+2)+(6+a4)-1，所以a4=4，an+2=n+2，又a1=1，a2=2,a3=3，所以an=n.

4.已知an=2n-1，Sn=2n-1.

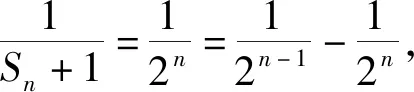
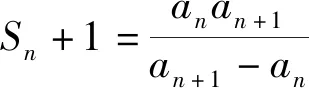
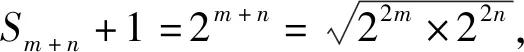
题6 已知各项均为正数的数列{an}，其前n项和为Sn，a1=1，a2=2，a3=4，且满足(Sm+n+1)2=(S2m+1)(S2n+1)，其中m,n为任意的正整数，求数列{an}的通项公式.

解：因为an>0，所以Sn>0，Sm+n+1=

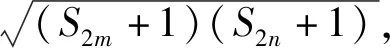
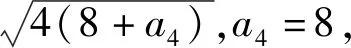
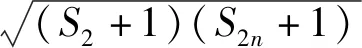
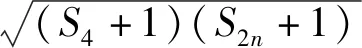
(三)利用等差、等比数列的性质构造

5.在等差数列{an}中，若m+n=p+q，则am+an=ap+aq，特别地an-1+an+1=2an，an-2+an+2=2an，思考已知an-2+an-1+an+1+an+2=4an，能否证明{an}是等差数列，显然不能判断，若再满足an-3+an-2+an-1+an+1+an+2+an+3=6an，可得：

题7 (2017年江苏高考)对于给定的正整数k，若数列{an}满足an-k+an-k+1+…+an-1+an+1+…+an+k-1+an+k=2kan对任意正整数n(n>k)总成立，则称数列{an}是“P(k)数列”． 若数列{an}既是“P(2)数列”，又是“P(3)数列”，求证：{an}是等差数列．

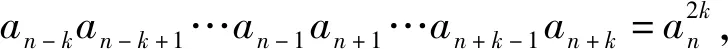
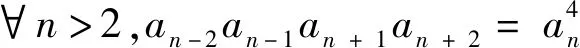
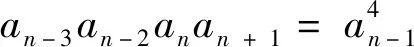
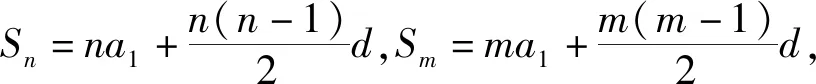
题8 已知数列{an}的前n项和为Sn，若∀m,n∈N*，(n-m)Sm+n=(n+m)(Sn-Sm).求证：数列{an}为等差数列.

证明:令m=1可得(n-1)Sn+1=(n+1)(Sn-S1)，整理可得2Sn=(n-1)an+1+(n+1)S1①，当n≥2时，2Sn-1=(n-2)an+nS1②，①-②得2an=(n-1)an+1-(n-2)an+S1，整理可得nan=(n-1)an+1+S1③，当n≥3时，(n-1)an-1=(n-2)an+S1④，③-④得(n-1)an+1-2(n-1)an+(n-1)an-1=0，因为n-1≥2，所以当n≥3,an+1-2an+an-1=0，③式中取n=2，可得a3-2a2+a1=0，所以对∀n≥2，an+1-2an+an-1=0恒成立，所以数列{an}为等差数列.

命题是一项复杂的系统工程，对命题的认识与理解需要不断实践思考与总结.作为教师，面对试题不能仅仅满足于如何去解，更应思考众多优美的试题是如何命制的.了解试题背后的命题思路与想法，才能对其有更深的理解，从而有针对性的进行变式练习，真正提高学生的数学素养.