过程性变式视角下数学抽象素养的培养——以2020全国高考数学卷Ⅰ理科20题为例

江苏省灌南高级中学 (222500) 翟海军 刘鑫钧

一、试题及母题呈现

1.试题再现

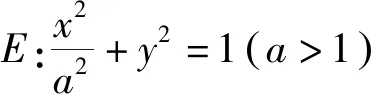
2.解法探究

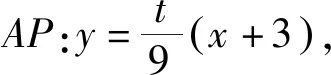
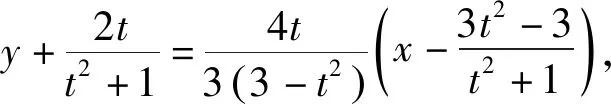
这道题并非空中楼阁，事实上此题无论在条件、结论、解法等方面均与下面这道江苏高考题非常吻合.

3.母题呈现

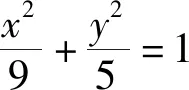
二、问题提出及解决

解题教学不能停留在就题论题的层面，而应该通过对一道或几道试题的探究实现对一类问题的解决，这就需要引导学生进一步深入思考：上述两道高考题之间的联系是什么？能否抽象出更一般的模型？怎样从数学问题中抽象数学模型？有哪些模型？模型之间的联系与区别是什么？只有解决了这些问题才能使学生理顺思路，开阔视野，实现对问题的深度理解，从而使数学抽象素养在课堂教学中真正落地.本文以2020全国Ⅰ卷理科20题为例，探索如何在过程性变式视角下提高学生在模式识别、模式提炼、模式整合等方面的能力从而培养学生的数学抽象素养.

1.运用图式表征实现模式识别

《普通高中数学课程标准(2017)》(以下简称《标准》)指出，高中数学教学以发展学生数学学科核心素养为导向，创设合适的教学情境，启发学生思考，引导学生把握数学内容的本质.这样在课堂教学中要善于引导学生用数学语言表征问题，继而抽象出一般规律和结构.这里将2020全国Ⅰ卷理科20题记为试题1，2010江苏高考18题记为试题2.试题1用图1来表征.试题2用图2来表征.

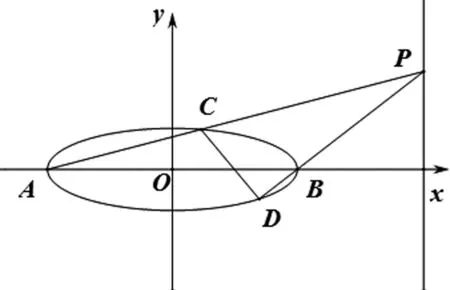
图1

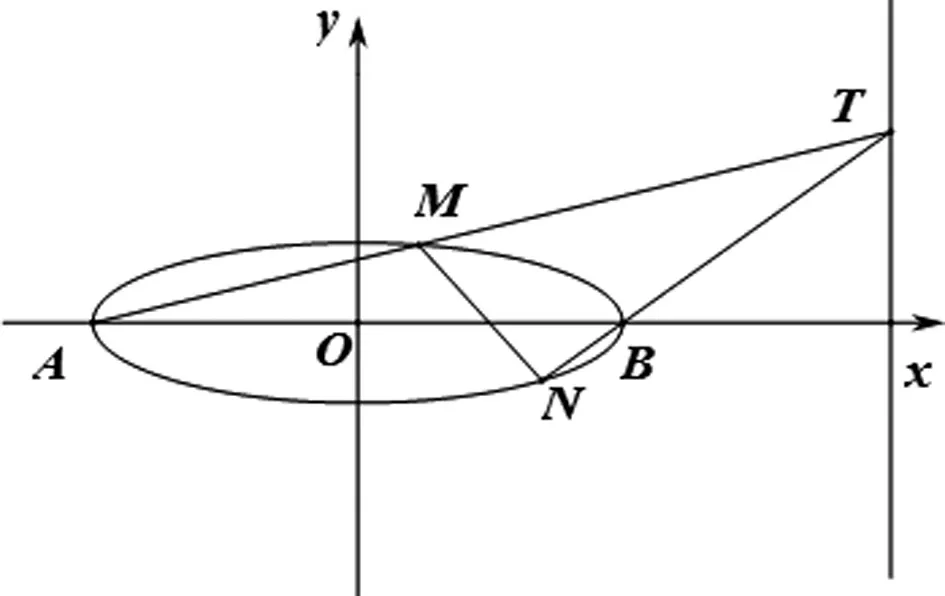
图2

通过对图1与图2中椭圆位置形态及点、线之间关系的观察与比较，学生很容易发现两个问题的一致性：两个题目都是过椭圆外一条垂直于x轴的直线上一动点，连接该动点与椭圆的左、右顶点，然后得到两条直线，这两条直线分别与椭圆相交于另外两点，最后都是证明：过两点的直线必定经过平面内一定点. 问题的相似性激发着学生对问题模型的提炼，从而抽象出以下一个基本的模型.

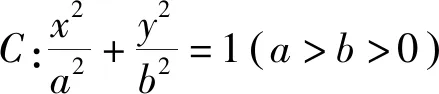
2.立足过程性变式逐级抽象模型

《标准》要求，学生能在情境中抽象出数学概念、命题、方法和体系，积累从具体到抽象的活动经验；养成在日常生活和实践中一般性思考问题的习惯，把握事物的本质，以简驭繁.那么在平常的解题教学中如何落实呢？过程性变式教学是落实目标的一种有效方式.

顾泠沅等学者把变式教学分为概念性变式和过程性变式教学两类.概念性变式教学突出对概念内涵的理解，过程性变式教学突出对概念外延的应用，注重知识之间的联系和拓展，通过过程性变式教学，使数学教学有层次地递进[1]. 利用过程性变式可以对一个初始问题进行变式，继而提出数学命题和模型，从而使得数学抽象素养在课堂教学中落实.

(1)改变直线位置 抽象定点模型

在教学过程中，可以让同学们思考试题1中动点P在变化过程中不变的是什么？在学生发现点P始终在一条竖线上运动后，顺势追问：你认为点P还可以在哪运动，哪些地方需要做相应的改动，学生容易想到将竖线变为横线，基于对称性，长轴的端点需改为短轴的端点，从而得到下面这个变式.

变式1中的点P是在一条横线上运动，但是直线MN仍然过一定点.基于对数学问题统一性的追求，可以向学生提问：你能将这两种情况概括一下吗？由此抽象出模型2.

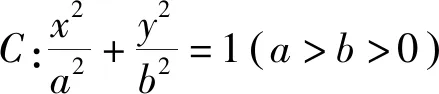
(2)转换条件与结论 抽象定线模型

探索问题的脚步可以继续下去，在模型2中点P在定线上，最后发现直线MN过定点，概括起来就是：定线产生定点.因此可以追问学生：反过来我们还可以研究什么问题？让学生独立思考，大胆猜想，合作交流，学生提出这样一个问题：如果直线MN过定点，那么AM与BN的交点是否在一条定直线上？

事实上，这个结论是正确的,而且定直线恰好为x=6，这时教师可以追问：如果点Q为y轴上一定点，是否也有相应的结论？最后基于追求问题的统一性，教师可以向学生提出一个问题：你能将上述两种情况的结论概括一下，从而抽象出模型3.

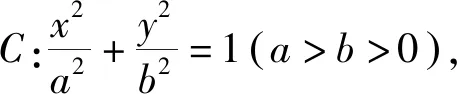
(3)整合相关问题 抽象定值模型

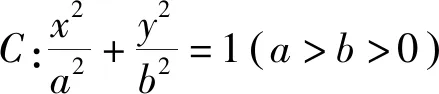
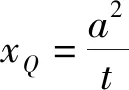
通过对试题1的不断抽象，引导学生提炼出定值、定点、定线三类模型，让学生对问题有了进一步深入的理解，提高了学生对这三类模型之间的联系与区别的认识，使得数学抽象素养在课堂教学中得以有效的渗透.

三、结语

教师在平常的解题教学过程中不仅要让学生获得问题的解决，更应当培养学生对一类问题解决的能力，这就需要培养学生的数学抽象素养.运用过程性变式可以让学生感悟共相，提炼本质，提高学生对一类问题模型的识别与概括能力，从而使得学生的数学抽象素养在解题教学中得以落实.