黄沙百战穿金甲 不破楼兰终不还*——拙文[1]“知其然，更要知其所以然”反思

福建省厦门第一中学 (361003) 王淼生福建省厦门市五显中学 (361100) 叶建聪

1 原题再现

文[1]对学生胡亿权提出的一道试题进行了初步探究．为了便于后续论述，再将原题呈现，原题如下(以下简称案例1)：

案例1 已知函数f(x)=x3+ax+b定义域为[-1，2]，记|f(x)|的最大值为M，则M的最小值为( ).

无独有偶，前不久我校作业也出现这样一道试题，原题如下(以下称案例2).

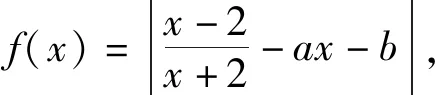
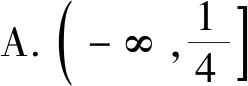
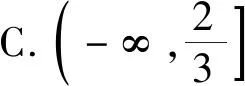
对于案例2，备课组提供以下参考答案：

记y=f(x)(x∈[-1，2])的最大值为M(a，b)，由题意可知m≤M(a，b)对任意的实数a，b恒成立，所以m≤M(a，b)min．

显然，M(a，b)≥f(x)(x∈[-1，2])，分别取x=-1，x=0，x=2得

6M(a，b)=2M(a，b)+3M(a，b)+M(a，b)

≥|-6+2a-2b|+|-3-3b|+|-2a-b|

≥|(-6+2a-2b)-(-3-3b)+(-2a-b)|=3

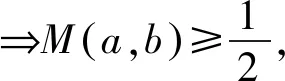
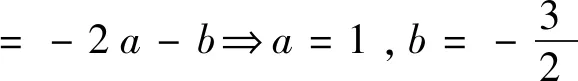
2 形异质同

学生胡亿权仿照上述提供的案例2解答过程，重新构思案例1：

记y=|f(x)|(x∈[-1，2])，由题意|f(x)|最大值为M，由于含有参数a，b，因此此处M即为M(a，b)，设M(a，b)的最小值为m，则m≤M(a，b)对任意的实数a，b恒成立，所以m≤M(a，b)min，……

案例2与案例1看似表现形式不尽相同(案例1求最小值；案例2求取值范围)，但其本质却是一样，因此案例2再一次引起笔者高度关注．

3 激烈讨论

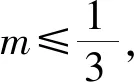
备课组长周翔老师及时将学生反馈的信息汇总，并根据案例2的外形结构与本质特征，以视频的方式向高三全体学生展现数形结合的剖析过程，其解答过程正是本文后续第9部分“简捷解答”中“第9．2部分：妙解案例2”的雏形．

4 理论依据

回顾拙文[1]，仅仅只是立足高中数学知识层面，借助特殊值(即赋值法)的视角就事论事而已．冷静思考，以目前中学知识，确实很难再找到其它通性通法来处理类似于案例1、案例2等这类试题．哪命题专家如何能够命制出妙不可言的案例1与案例2？命题出发点是什么？究竟要考查什么知识点？理论依据又是什么？正是受到周老师的启发以及学生孙睿的提醒，笔者联想到近年来各级各类考试中、试卷里频频出现的“高观点”试题．

4．1 “高观点”试题

所谓“高观点”试题，是指与高等数学密切相关的数学试题．这类试题或借助高等数学知识为理论背景，或体现高等数学中常用的数学思想，或运用高等数学成熟的推理方法．“高观点”试题主要表现形式为：语言叙述“高观点”，知识背景“高观点”，能力方法“高观点”，等等．“高观点”试题命题策略：高等数学初等化、初等数学高等化及初高等数学交汇化．通俗地讲，高等数学“搭台”，高中数学，甚至初中数学乃至小学数学“唱戏”．

毋容置疑，部分高等数学知识的引入，为我们解决初等数学许多问题提供了方法指导与理论依据(比如，引入导数为研究初等函数性质如虎添翼)，而且恰当的、适度的“高观点”试题有利于和谐初等数学与高等数学知识无缝对接，有助于提高学生独立分析问题与解决问题能力，有益于优化学生数学思维品质与培养数学学科核心素养．

4．2 “高观点”理论

(1)拉格朗日中值定理

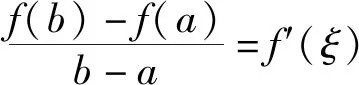
评注：尽管中学没有明确教授拉格朗日中值定理，但是中学生很容易接受拉格朗日中值定理.因为拉格朗日中值定理几何意义特别明显：满足条件的函数f(x)的曲线上至少存在一点，过该点处的切线与该曲线两个端点的连线平行.

(2)函数凸凹性定义

若f(x)是定义在区间I上的连续函数，对任意实数x1，x2∈I，且0<λ<1，总有f[λx1+(1-λ)x2]≤(或≥)λf(x1)+(1-λ)f(x2)，则称f(x)为定义在区间I上的下凸(或上凸)函数．

由定义可知f(x)为区间I上的下凸(或上凸)函数⟺f′(x)为定义在区间I上的增(减)函数⟺f(x2)≥(≤)f(x1)+f′(x1)(x2-x1)⟺f″(x)≥0(f″(x)≤0)恒成立．

(3)切比雪夫最佳逼近直线

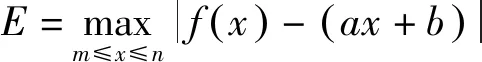
设A={g(x)=ax+b|a∈R，b∈R}，若存在函数g0(x)∈A使得对任意g(x)∈A，恒有

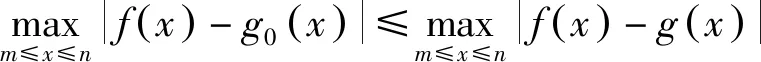
当然，①还可以写成等式形式，即

4．3 命题依据

由切比雪夫最佳逼近直线定义，并结合拉格朗日中值定理及函数凸凹性定义得到以下基本结论：

结论1 若f(x)是定义在区间[m，n]上的连续函数，且f″(x)在区间(m，n)上不变号，则f(x)最佳逼近直线存在且唯一.

结论2 直线g(x)是连续函数y=f(x)(x∈[m，n])的最佳逼近直线的充要条件是g(x)至少具有三个偏差点，且它们依次轮流为正负偏差点.

结论3 若f(x)是定义在区间[m，n]上具有二阶导数，且f″(x)在区间(m，n)上不变号，则f(x)最佳逼近直线为

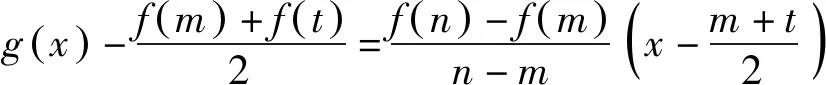
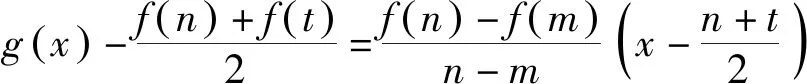
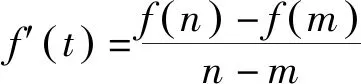
(2)显然，③与④等价．其实上结论3为精准求出最佳逼近直线(或者说解答这类试题)提供了具体的操作步骤：首先，求出区间两个端点A与B连线的斜率kAB及直线(割线)AB的方程；其次，通过求导f′(t)=kAB，准确找到与直线AB平行的切线的切点C(t，f(t))及切线CG方程；再次，连接AC(或BC)，取AC中点为D(或BC中点为E)；过D(或E)且平行直线AB的直线就是所求的最佳逼近直线DE，即上述③(或④)；最后，直线DE与直线AB或者直线DE与切线CG之间的“落差”就是偏差最大值的最小值．

5 试题特点

5．1 案例1与案例2特点

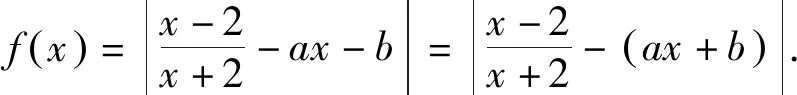
5．2 试题特点归纳

这类试题主要特点：由定义在闭区间[m，n]上的连续且可导函数h(x)，且h″(x)不变号(或者在相应区间上，与区间端点连线平行的曲线切线是唯一的)；含有两个参变数的一次函数φ(x)=ax+b，它们构造的函数ω(x)=|h(x)-φ(x)|，求函数ω(x)的最大值的最小值．通过上述剖析，说明拉格朗日中值定理、函数凸凹性、切比雪夫最佳逼近直线及上述结论正是专家命制案例1与案例2的“高观点”理论依据．据此说明上述案例1与案例2完全符合上述偏差定义，也就是说，我们完全可以按照上述结论3来破解案例1与案例2．

5．3 妙解案例1及2

依据上述“高观点”理论依据与上述结论3操作步骤可知：端点A(-1，-1)，端点B(2，8)，则kAB=3，此时直线(割线)AB方程为y=3x+2．又因为kAB=f1′(t)(t∈(-1，2))⟹t=1(t=-1舍去)．故切点C(1，1)，此时切线方程为y=3x-2．线段AC中点D(0，0)，最佳逼近直线为y=3x．无论是y=3x-2与y=3x，还是y=3x+2与y=3x偏差的绝对值均为2，此时案例1中的g1(x)=3x，所求M的最小值为2，故选C．

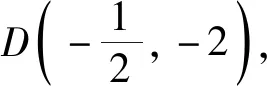
6 终破楼兰

6．1 是否渗透高等数学背景？

从文[1]及上述剖析过程不难看出案例1与案例2确实属于“高观点”试题，与拉格朗日中值定理、函数凸凹性以及切比雪夫最佳逼近直线等高等数学知识、方法相关，可以猜想案例1与案例2就是依据上述这些高等数学知识而命制的，主要考查切比雪夫最佳逼近直线等相关知识与解题方法．鉴于平时教学中没有渗透这些高等数学知识，因此部分同学没有弄懂案例2的本质，不会解答这类试题，也属正常现象．

6．2 区间相同是偶然还是必然？

由案例1与案例2的简捷解答过程可知，命题专家在保证函数连续、可导等条件的前提下，之所以选择区间[-1，2]，应该是出于考虑计算简单，没有其它用意，完全可以给定其它区间，只不过运算量大一些而已．至于案例1与案例2给出相同的区间[-1，2]，纯属偶然，没有必然联系．也就是说，设置的区间必须满足闭区间、函数有意义、连续、二阶导数不变号及便于计算即可．

6．3 能否破解文[1]“未解之谜”？

没有规矩则没有方圆，数学更是如此．从上述拉格朗日中值定理、函数凸凹性以及结论3便知，这些定理与结论都是在设置相应的闭区间的前提下而得到的．也就是说我们首先连接所给区间端点线段，就是为了从整体上把控所要研究的整段曲线．如果首先不控制区间端点，显然失去研究意义与价值，这就解释了特殊值为何一定要取区间端点，也回应了拙文[1]结尾提出的“未解之谜”．

6．4 是否特殊值越多越准确？

如果我们把取闭区间两个端点的值看作第一个、第二个特殊值，那第三个特殊值如何取？可以任意取吗？还需要取第四个特殊值吗？是不是特殊值越多就越准确？

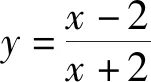
需要特别指出的是：结论3之所以要求“f″(x)在区间(m，n)上不变号”，其目的在于确保与区间[m，n]端点连线平行且与曲线相切的切线唯一(切点唯一)，从而确保函数f(x)最佳逼近直线是唯一的(比如案例2)．值得特别说明的是，这一条件只是充分并非必要条件．比如案例1中的函数y=x3，其二阶导数y″=6x在(-1，2)变号(可正可负)，但其在x∈(-1，2)内切线只有一条，即本文5.3部分“案例1解答”中的唯一切点的横坐标x=1，同样能够确保该函数的最佳逼近直线依然唯一．

本文与拙文[1]形成姊妹篇．笔者从中数视角(赋值法)及高数视野(高观点)双管齐下，相互辉映，圆满解决了类似于案例1、案例2这类问题(最佳逼近直线)，正所谓“黄沙百战穿金甲，不破楼兰终不还．”