以最大slice态为信道的受控量子远程控制

彭家寅

内江师范学院 数学与信息科学学院，四川 内江641199

量子纠缠是量子计算和量子信息理论的核心，它被用作执行诸如量子安全直接通信[1-2]、量子密钥分配[3]、量子对话[4]、量子签名[5]、量子隐形传态[6-7]、量子态分享[8]、量子信息集中[9-10]和远程态制备[11-12]等量子任务的物理资源。在这些量子任务中，纠缠的一个引人注目的应用是由Bennett 等于1993 年提出的量子隐形传态[13]，它允许以Einstein-Podolsky-Rosen对为量子信道来实现任意单量子态的隐形传输。除量子隐形传态外，量子纠缠还允许人们将任意的酉算子从发送者Alice 传送给遥远的接受者Bob，以操控某些量子态。称这种量子算子的传输为量子算子的远程实现（有时也称它为量子远程控制），它将在分布式量子计算、大规模量子模拟、量子程序或其他远程量子信息处理任务中发挥重要作用。Huelga等[14]提出的第一个量子远程控制方案，探索了在遥远的量子系统上传输任意酉算子的方法。即Alice可以对位于远处的Bob 所持有的量子态实施任意酉运算U，这个任务通过双向量子态隐形传态来完成。随后，一些量子远程控制的理论方案被提出[15-20]，并且用线性光学元件也证明了单光子的远程旋转可以实验实现[21]。值得指出的是，当酉算子是完全未知的时候，才需要双向隐形传态来实现量子远程控制；而当酉算子取自某些限制集时，则需要较少纠缠资源且无需双向隐形传态就能实现量子控制[15-16,19-21]。为了提高量子远程控制协议的安全性，Wang于2007年率先提出了一个关于部分未知酉算子的受控远程执行方案[22]。此后，利用不同量子纠缠资源的酉算子的受控传输协议被报道[19,23-26]。

近年来，人们对一类特殊的部分纠缠态——最大slice（MS）态——进行了研究[27]。2008年，Gao等[28]利用三量子MS态

的受控联合远程态制备协议。

Zhou 等[31]讨论了基于MS 态信道的受控远程实系数多量子态的制备。本文以三粒子MS态为信道，研究任意单量子酉算子的远程执行问题。仅当与控制者合作，一个任意单量子酉算子才能在接受者的量子系统上被远程地执行。此外，还讨论取自限制集的部分未知酉算子的受控远程执行问题。

1 任意单量子酉算子的受控远程实现

其中，a和b是实数，且满足归一化条件a2+b2=1。该态中量子C与量子B、A之间的纠缠度由参数b确定。如果b=0，则：

其中，s,t=0,1，⊕表示模2 的加法。常用的Pauli 算子可写成：

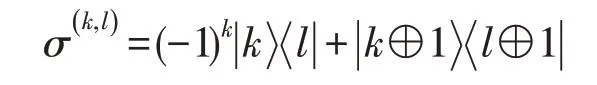
其中，k,l=0,1。

本章的量子任务是在监控者Charlie 的控制下，发送者Alice 把一个任意未知单量子酉算子Uτ应用到遥远的接受者Bob 的量子系统上。具体地，假设Bob有处于如下量子态的量子B′：

其中，j=1,2，量子A1和A2属于发送者Alice，量子B1和B2属于接受者Bob，而量子C1和C2属于控制者Charlie。

为完成量子任务，本协议设计成如下连续6步来完成。

这表明通过上述6步后，单量子远程控制任务就完成了，并且成功的概率为100%。

2 部分未知单量子酉算子的受控远程实现

众所周知，在量子信息处理中，所需的量子纠缠和经典通信耗费扮演着十分重要的角色。在量子远程控制中，如果被执行的量子算子是部分未知酉算子，那么经典通信和量子纠缠耗费是可以减少的。本章考虑利用三量子MS态为信道，取自两个限制集的部分未知酉算子的受控远程执行问题。

文献[15]给出了取自限制集的部分未知酉算子Ud(d=0,1)为：

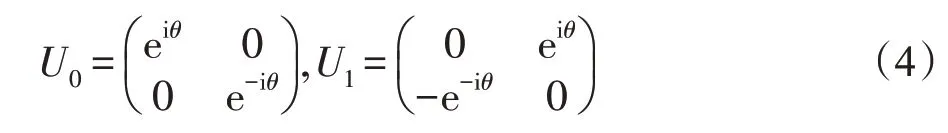
其中，θ是任意实数。换言之，矩阵中非零元素的值是未知的，而矩阵的结构——非零元素的位置——是已知的。

对于酉算子Ud的受控远程执行，Alice、Bob 和Charlie 如第1 章那样预先分享一个三量子MS 态（1），即量子A属于发送者Alice，量子B属于接受者Bob，而量子C属于控制者Charlie。此外，Bob 有处于态（3）所示的量子B′。由量子A、B、C和B′构成的初始系统总态为：

其中，k,l=0,1。然后，Alice 对量子A执行如式（4）所示的部分未知酉算子Ud(d=0,1)，则式（6）所示态变成：

3 结论

本文研究了基于三量子最大slice态为量子信道的单量子态之远程控制问题，提出了酉算子的受控远程执行的两个协议。在第一个协议中，通过非最大纠缠量子信道以及所有参与者的合作，任意单量子酉算子能够在遥远接受者的量子系统上被远程地执行。当发送者和控制者对各自量子施行适当的投影测量时，该受控量子远程控制方案的成功概率达到1。在第二个协议中，利用非最大纠缠态作为量子信道，提出了确定性的部分未知单量子酉算子之受控远程执行方案。结果表明，如果被远程执行单量子酉算子取自于两个限制集，那么量子纠缠和经典通信耗费都能减少。

在本文所提出的两个方案中，尽管量子信道是非最大纠缠的，但单量子酉算子的受控远程执行协议的成功概率仍然达到了1，它等于以最大纠缠态为信道的受控量子远程控制协议[32]的概率。不同于基于非最大纠缠信道的方案[33]，本文方案不需要引入辅助量子去改变信道为目标信道。产生上述两个结果的原因是作为量子信道的MS态：

去测量自己的量子C，则发送者和接受者的量子的态总是塌陷成两个最大纠缠的Bell态

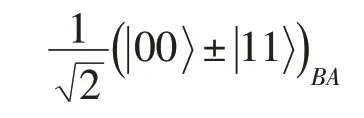
之一。当控制者通过经典信道公布自己的测量结果时，发送者和接受者就会知道他们分享的具体Bell态，并且用它就可以进行标准的量子远程控制。因此，这样的方案不需引入辅助量子，且成功的概率和保真度都为1，而与量子信道的纠缠度无关。