增量式约简最小二乘孪生支持向量回归机

曹 杰，顾斌杰，熊伟丽，潘 丰

江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡214122

支持向量机（support vector machine,SVM）自20世纪90 年代由Vapnik[1]提出以来，受到广泛的关注。SVM的主要思想是通过最大化间隔实现结构风险最小化，使得模型具有良好的学习性能和泛化性能[2-3]。目前，SVM 已经成功运用到特征选择[4]、文本分类[5]、时间序列预测[6]、目标跟踪[7]和行人检测[8]等领域。之后，Collobert 等人[9]把支持向量机的思想用于解决回归问题，提出了支持向量回归机（support vector regression，SVR）。

近年来，SVM 又衍生出了新的算法。2007 年，Jayadeva等人[10]提出了孪生支持向量机（twin support vector machine，TSVM）。TSVM 通过求解两个小规模的二次规划问题，构建两个非平行超平面，训练时间缩短到原SVM的1/4左右，并且同样具有很好的泛化性能。2010 年，Peng[11]基于TSVM 的思想，提出了孪生支持向量回归机（twin support vector regression，TSVR），通过寻找两个非平行的超平面，构建回归模型。实验结果表明，TSVR在训练速度以及泛化性能方面均优于传统SVR。因此，TSVR迅速成为了支持向量机领域的研究热点。同年，Singh 等人[12]提出了约简孪生支持向量回归机，通过随机选择部分支持向量构成行列不等的核矩阵，获得稀疏解，加快了训练和预测的速度，但预测精度有所降低。2013 年，Shao 等人[13]提出了ε-孪生支持向量回归机，不仅改进了损失函数，还通过添加正则化项实现了结构风险的最小化。2014年，卢振兴等人[14]提出了最小二乘孪生支持向量回归机，用等式约束代替不等约束，极大地加快了训练的速度。2016 年，Rastogi 等人[15]提出了v型孪生支持向量回归机，通过在目标函数中引入vε项，把不敏感参数ε作为变量，实现了自动控制ε的目的。

然而，以上方法都是关于离线训练算法的研究。在实际应用中，由于数据的更新会使旧模型失效，无法满足实际的需要。而增量学习算法能够充分利用历史的训练结果，减少模型更新所需要的时间，能够很好地解决时变问题。目前为止，在增量式SVM 以及增量式SVR 的研究上，学者们取得了很多研究成果，如Cauwenberghs 等人[16]提出的增量式与减量式SVM，何丽等人[17]提出的自适应SVM 增量算法，Ma等人[18]提出的精确在线支持向量回归机，以及顾斌杰等人[19]提出的精确增量式在线ν型支持向量回归机，都是在原有模型的基础上通过少量迭代，更新模型，使得所有样本满足KKT条件。此外，张浩然等人[20]提出了最小二乘支持向量回归机的增量学习算法，Zhao 等人[21]提出了在线不相关约简最小二乘支持向量回归机，避免了求解二次规划问题，算法的实时性得到很大的提升，并且后者能够获得稀疏解，使得预测速度也得到了提升。

目前为止，关于增量式孪生支持向量回归机的研究并不多见。2016年，郝运河等人[22]提出了增量式最小二乘孪生支持向量回归机。该方法基于最小二乘孪生支持向量回归机模型，在增量之前，随机选取部分支持向量生成预训练模型，在接下来的增量过程中，只增加核矩阵的行向量而不增加核矩阵的列向量，因此求解过程中逆矩阵的维数不变，加快了增量更新模型的速度，并且使得模型解的规模不变。但是这样获得的核矩阵可能会忽略掉原核矩阵中的线性无关的列向量，使得核矩阵无法很好地逼近原核矩阵，导致模型的泛化性能与离线算法相比大大下降。为此，本文提出一种增量式约简最小二乘孪生支持向量回归机算法（incremental reduced least squares twin support vector regression,IRLSTSVR）。IRLSTSVR

算法尝试利用约简方法，选取使核矩阵中列向量线性无关的样本作为支持向量，构建行列不等的核矩阵，并且通过分块矩阵求逆引理，充分利用已知计算结果高效更新逆矩阵，在保证模型解的稀疏性的同时，更好地逼近离线算法的泛化性能。最后通过实验，验证算法的可行性和有效性。

1 最小二乘孪生支持向量回归机

最小二乘孪生支持向量回归机用等式约束替代不等约束，并加入正则项，把经验风险与结构风险相结合，寻找下界回归函数和上界回归函数，其中，ω1,ω2∈Rm为权重向量，b1,b2∈R 为偏置，即得到两个非平行的超平面。因此，线性回归问题可以表示为如下约束最优化问题[14]：

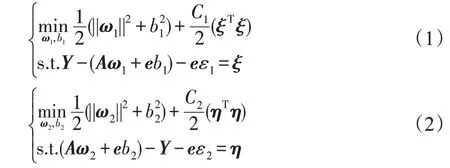
其中，C1,C2＞0 为正则化常数，ε1,ε2＞0 为不敏感因子，ξ,η∈Rn为松弛向量，e为相应维数元素全为1的列向量。

其中，I为相应维数的单位阵。

因此，对于某一测试输入x，可以通过式（7）预测其对应输出：

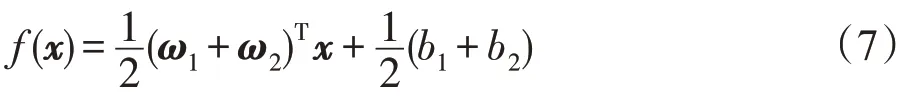
在解决非线性回归问题时，需要借助核函数K(·,·)，将样本从原始空间映射到一个更高维度的特征空间，则此时的下界回归函数为f1(x)=K(xT,AT)ω1+b1，上界回归函数为f2(x)=K(xT,AT)ω2+b2，其中ω1,ω2∈Rn，b1,b2∈R。

令G=[e K(A,AT)]，则非线性回归问题目标函数的解也可以表示为式（5）和式（6）的形式。对于某一测试输入x，其对应输出如下：

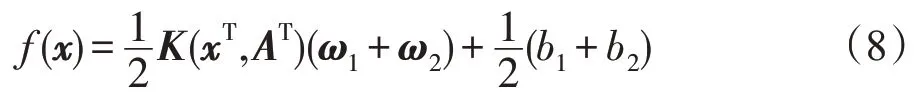
2 增量式约简最小二乘孪生支持向量回归机

对于线性回归问题，模型解的规模只和样本的特征数有关，即输入量的维数。如果输入量维数过高，可以预先进行降维，再通过文献[22]中的方法进行增量训练，本文不再赘述。然而，对于非线性回归问题，随着样本个数的增加，支持向量的个数和解的维数会不断增加，导致一次增量更新所需的时间和模型预测所需的时间快速增长，无法满足实际应用中实时性的要求。此外，现有的增量式最小二乘孪生支持向量回归机通过随机选取支持向量构建预训练模型的方法，可能会导致忽略了一些特征相异的样本，保留了一些特征相似的样本，使得核矩阵丢失了原核矩阵中线性无关的列向量，不能很好地逼近原核矩阵。

因此，本文针对非线性回归问题，尝试利用约简方法，选择特征相异的样本，使得构建的核矩阵能够保留原核矩阵中线性无关的列向量，以便更好地逼近原核矩阵。最后以约简后的列线性无关的核矩阵为基础，通过增量方法，构建约简最小二乘孪生支持向量回归机模型。

2.1 约简方法

在约简过程中，把训练样本分为三个集合，分别为约简集S、约束集P和无关集O。其中，约简集S为约简后作为支持向量的样本集合，该集合中样本的特征差异性较大，它的样本个数即为核矩阵的列数；约束集P为约简集S中的样本以及预测值误差较大的样本的集合，它的样本个数即为核矩阵的行数；无关集O为预测值误差较小的样本集合。在增量过程中，忽略无关集O中的样本。

假设在t时刻模型的S集合中有l1个m维样本，P集合中有l2个m维样本，并且P集合包含S集合，即l1≤l2，S集合的样本矩阵为ASt，P集合的样本矩阵为APt，核矩阵为。

在t+1 时刻，新增一个样本(xn+1,yn+1)，如果把该样本同时加入S集合和P集合中，则形成的新的核矩阵如下：

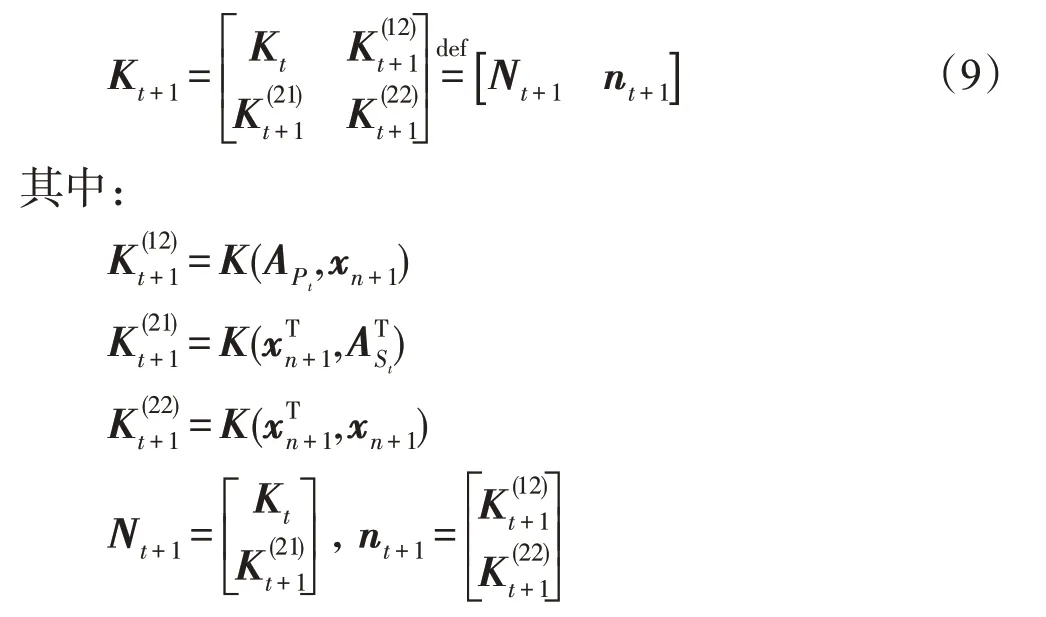
在选择同时加入到S集合和P集合中的样本时，需要考虑的就是核矩阵Kt+1中的列向量nt+1和矩阵Nt+1中的列向量是否线性相关，即式（10）是否有解：

其中，αt+1∈Rl1为线性方程组式（10）的解。

由于精确的线性相关要求会导致数值的不稳定性，因此通过求解如下最小化问题来近似判断线性相关关系：

把式（13）代入式（12），可求得αt+1的值。

最后，将αt+1的值代入式（11）可求得目标函数的值。

若式（11）的值约等于0，则列向量nt+1和矩阵Nt+1中的列向量线性相关。在实际算法中，设置约简常数λ∈(0,1)和δ(αt+1)进行比较。如果δ(αt+1)＞λ，则列向量nt+1和矩阵Nt+1中的列向量线性无关，新增样本(xn+1,yn+1)同时添加到S集合和P集合，否则需要通过式（14）判断样本是否位于t时刻模型上界函数和下界函数之间：

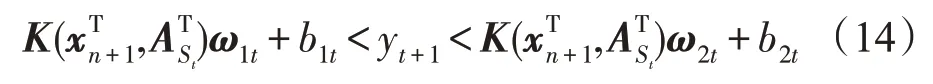
如果不满足式（14）则说明t时刻模型不满足当前需求，新增样本(xn+1,yn+1)需要添加到P集合中，否则新增样本(xn+1,yn+1)添加到O集合中，无需更新模型。

在明确当前新增样本的所属集合之后，为了判断下一次新增样本的所属集合，以下两种情况需要更新Kt+1和Mt+1：

情况1新增样本添加到S集合和P集合中，Kt+1更新同式（9），Mt+1的更新公式如下：

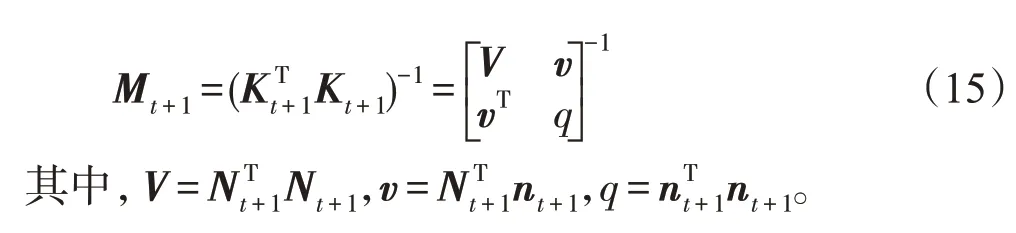
引理2设A是n×n的可逆矩阵，b是n×1 的向量，d是标量，且d-bTA-1b≠0，则有：

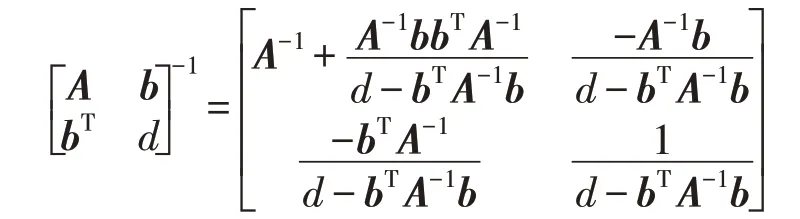
引理2的证明见文献[24]，此处省略。

令Z=V-1v，J=q-vTZ，则由引理2可得：

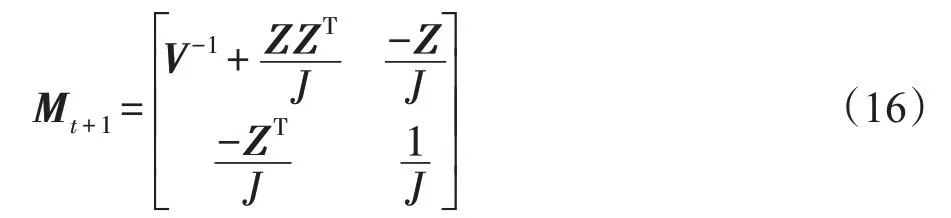
式（16）中的V-1由式（13）通过引理1 求得，而J为一个标量，因此整个更新无需矩阵求逆。

情况2新增样本只添加到P集合中，更新公式如下：

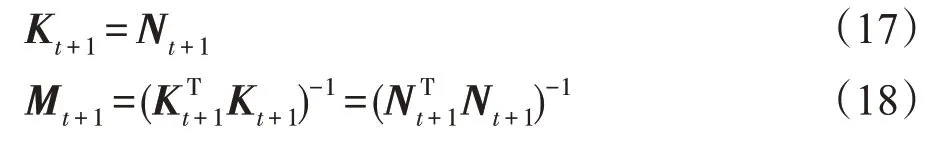
式（18）由式（13）通过引理1 获得，同样，以上更新过程无需矩阵求逆。

上述约简方法主要是针对核矩阵为半正定矩阵，存在线性相关的列向量的情况，对核矩阵进行约简。由于添加了线性相关的列向量，导致核矩阵中含有值为0的特征值，对应核矩阵中的冗余信息。因此剔除线性相关的列向量，在减小核矩阵规模的同时，可以获得一个近似原核矩阵的约简核矩阵。判断线性相关的一般方法为求解相应的线性方程组，但是线性方程组的等式要求过于严格，不便于求解。约简方法采用最小化问题替代线性方程组，度量新增列向量与核矩阵中已有列向量之间的相关程度，并且为了便于求解采用二次损失函数。如果线性相关，那么最小化问题会收敛到0 值附近，否则就会大于0值。

在实际操作中，采用非精确的线性相关性要求。当最小化问题目标函数的值小于一个接近于0的约简常数时，满足线性相关要求，该新增列向量不添加到约简核矩阵中，使得原核矩阵中约等于0的特征值被剔除。但是由于剔除的特征值并非严格为0，因此有效样本信息会有一定的损失。并且随着约简常数的增大，较大的特征值也被剔除，约简核矩阵的有效样本信息损失增大，列向量个数也会越少，相应解的规模也会越小。对于约简常数的设置，往往需要权衡核矩阵的样本信息损失和解的稀疏程度。

2.2 非线性增量式约简最小二乘孪生支持向量回归机

2.1 节详细阐述了划分S集合、P集合和O集合的方法，而非线性增量式约简最小二乘孪生支持向量回归机就是基于S集合和P集合构建的凸优化问题：

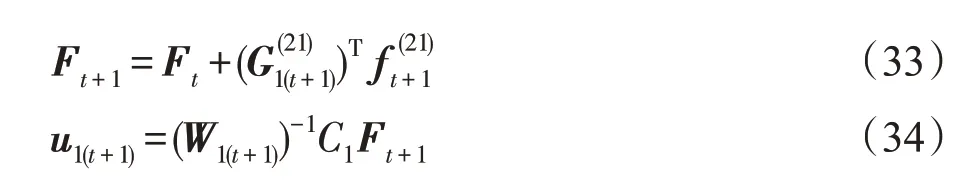
2.3 增量式约简最小二乘孪生支持向量回归机算法步骤

增量式约简最小二乘孪生支持向量回归机的步骤归纳如下，其中，步骤1～步骤3为模型初始化，步骤4～步骤7为增量更新模型：

步骤1设置参数C1、C2、ε1、ε2、λ。

步骤2把已有样本划分为S集合、P集合和O集合，并且计算Kt和Mt（详细方法见2.1节）。

步骤3由式（23）和式（24）计算t时刻模型的解u1t和u2t，同时保存模型更新时所需的量。

步骤4在t+1时刻，读入一个新的样本(xn+1,yn+1)。

步骤5由式（11）～式（13）可求得δ(αt+1)。

步骤6如果δ(αt+1)＞λ，则先由式（9）、式（15）和式（16）更新Kt+1和Mt+1，再由式（25）～式（30）求得u1(t+1)以及下一次增量更新所需的值，同理可得u2(t+1)及下一次增量更新所需的值；否则，判断式（14）是否成立，如果成立，则直接舍弃样本(xn+1,yn+1)；不成立则先由式（17）、式（18）更新Kt+1和Mt+1，再由式（31）～式（34）求得u1(t+1)以及更新下一次增量所需的值，同理可得u2(t+1)及下一次增量更新所需的值。

步骤7如果继续读入一个新样本，则重复步骤4～步骤6；否则，算法结束。

2.4 运算复杂度分析

针对2.1 节和2.2 节中阐述的增量过程，下面详细分析本文算法新增一个样本所需的时间复杂度。考虑到乘法的时间复杂度远高于加法，因此以下时间复杂度的分析只考虑算法所需乘法次数。此外，由于构造核矩阵的时间消耗是所有算法都不可避免的部分，本文算法并没有对此部分进行改进，故以下分析中不考虑构造核矩阵的时间复杂度。

综上可知，使用矩阵求逆引理进行增量求逆的时间复杂度为平方阶，而直接求解逆矩阵的时间复杂度为立方阶，因此使用矩阵求逆引理降低了算法的时间复杂度。此外，本文算法需要存储三个逆矩阵，逆矩阵的大小与S集合的大小有关。并且增量求逆方法对于近似奇异矩阵的求逆精度会有所下降，需要保证矩阵的正定性。

另一方面，本文算法的时间复杂度和l1、l2有关，而l1、l2大小能够分别由约简方法中的参数λ和ε1、ε2进行控制。本文算法能够在尽可能地降低精度损失的前提下，通过调节这三个参数进一步降低算法的时间复杂度。

3 数值实验与分析

3.1 实验设计

为了验证算法的可行性和有效性，选取离线最小二乘支持向量回归机（least squares support vector regression，LSSVR）[25]、离线最小二乘孪生支持向量回归机（least squares twin support vector regression，LSTSVR）[14]、增量式最小二乘孪生支持向量回归机（incremental least squares twin support vector regression，ILSTSVR）[22]和本文算法IRLSTSVR，在基准测试数据集上进行对比。所有实验在Intel i5-8300H（@2.30 GHz）处理器，8 GB 内存的计算机，Matlab2014a 软件平台上完成。

实验中使用的基准测试数据集如表1所示，其中最小规模为167，最大规模为9 568。Servo、Boston Housing、Concrete CS、Airfoil Self Noise、Abalone、Triazines 和CCPP 来 自 于UCI 数 据 库，PM10 和Space_ga来自于StatLib数据库。

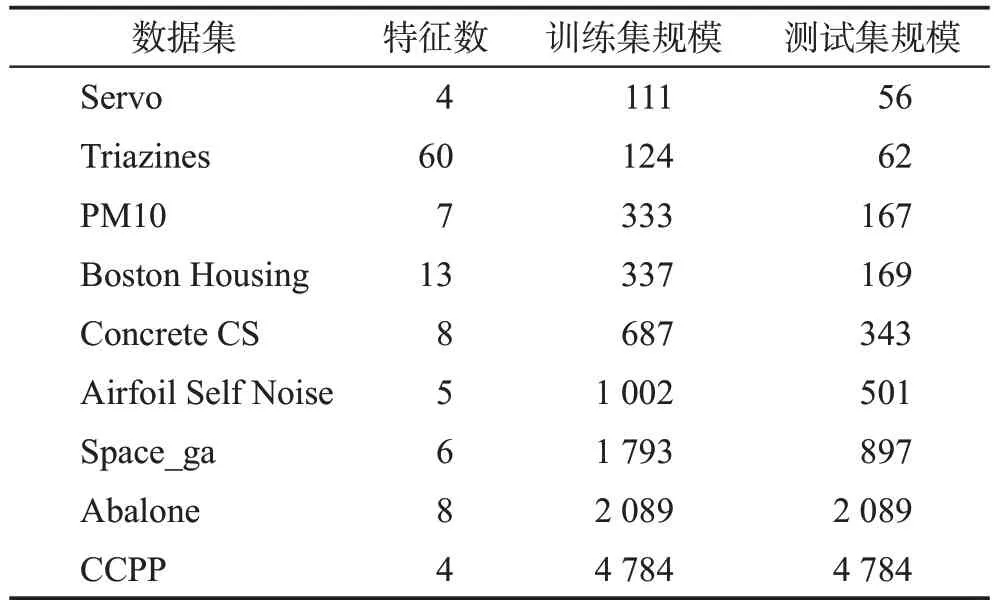
Table 1 9 benchmark datasets used in experiment表1 实验中使用的9个基准测试数据集

首先把每组数据集的输入数据归一化为[0,1]，然后划分训练集和测试集，在训练集上采用5次五折交叉验证的方式，共25 次实验的平均值进行参数寻优，最终以训练集上的最优模型在测试集上的表现来评判该模型的好坏。采用如下性能评价指标：

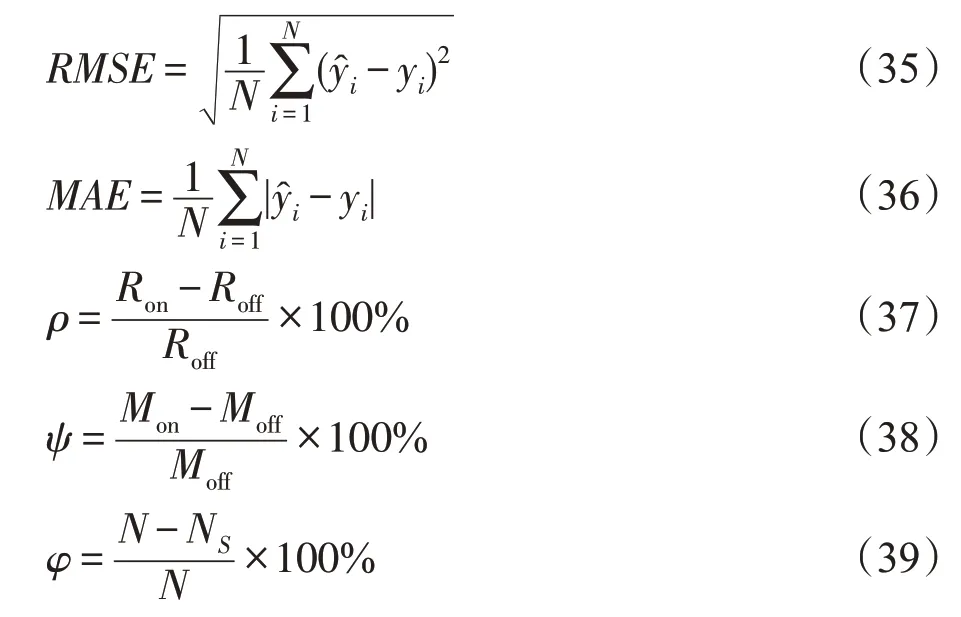
其中，RMSE为均方根误差；MAE为平均绝对误差；ρ和ψ分别表示RMSE和MAE的损失程度；φ为解的稀疏率；为第i个样本的预测值；yi为第i个样本的实际输出值；N为训练样本的个数；Ron为增量算法的RMSE；Roff为相应离线算法的RMSE；Mon为增量算法的MAE；Moff为相应离线算法的MAE；NS为S集合中样本的个数。

此外，还统计了S集合的样本个数NS和P集合的样本个数NP，平均一次增量所需的训练时间和最终模型对测试集进行预测所需的预测时间作为性能评价指标。

3.2 参数设置

为克服离线算法参数寻优的困难，在本文实验中，离线LSSVR 的参数C=2i，在i∈[-10,10]的范围内寻找最优值。离线LSTSVR的参数C1=C2=2i，在i∈[-10,10]的范围内寻找最优值，考虑到不敏感因子ε1、ε2对离线LSTSVR的影响较小[26-28]以及为了与离线LSSVR进行公平对比，取ε1=ε2=0.01。

对于本文算法，参数λ=10i，i∈[-5,-1]，在保证解的稀疏率的前提下，选择具有较优RMSE和MAE指标的情况。由于ε1、ε2的大小会对P集合的规模产生影响，并且ε1、ε2的设置不能够太大，实验中在相同λ下，选择ε1=ε2=0 的情况和ε1=ε2≠0 且使P集合的规模产生显著变化的情况，其他参数使用相应离线算法的寻优参数。对于ILSTSVR算法，随机选取和本文算法S集合大小相同的样本训练预训练模型，其他参数使用相应离线算法的寻优参数。核函数统一选取高斯径向基函数K(xi,xj)=exp(-||xi-xj||2/2σ2)，核参数σ=2i在i∈[-5,5]的范围内寻优。

3.3 实验结果与分析

表2 所示为选取的四种不同算法在基准测试数据集上的实验结果，其中IRLSTSVR 列举了两种情况，一种是ε=ε1=ε2=0 的情况，另一种是ε=ε1=ε2≠0 的情况，“—”表示该处指标无意义，粗体表示最优指标。

从表2 可以看出，对于本文算法，当ε=0 时，ρ最大为4.4%，Ψ最大为4.1%，φ最小为3.8%，最大为57%。当ε≠0 时，ρ最大为5.6%，Ψ最大为13%，φ最小为3.7%，最大为54%。对于ILSTSVR算法，ρ最大为135%，Ψ最大为97%，φ最小为3.8%，最大为57%。与离线LSSVR 和离线LSTSVR 相比，本文算法具有相近的泛化性能，解的稀疏性大为提高，预测时间减少以及平均一次增量更新所需的时间大为减少。与ILSTSVR相比，本文算法的泛化性能更好，更加接近离线算法，但是平均一次增量更新所需的时间略大。原因是本文算法在添加新样本时，进行了约简，考虑了核矩阵列向量之间的线性相关性。由于特征相似样本的添加会导致核矩阵中含有线性相关的列向量，利用凸优化问题来近似判断列向量之间的线性相关性，就能够排除特征相似的样本作为支持向量，获得一个与原核矩阵近似的约简核矩阵，有效减小模型解的规模获得稀疏解，减少预测时间。同时该约简核矩阵列向量对应的特征值都远大于0，含有原核矩阵绝大部分的信息，能获得和基于原核矩阵的离线算法相近的泛化性能；并且充分利用前一次更新时的计算结果，对矩阵求逆进行高效更新；此外和ILSTSVR不同，本文算法并不是只增加核矩阵的行数，当新添加的列向量线性无关时，需要计算添加了列向量与行向量后的逆矩阵，此时计算复杂度要高于只添加行向量的情况，而且多了约简部分的计算，因此本文算法更新时间会较长。

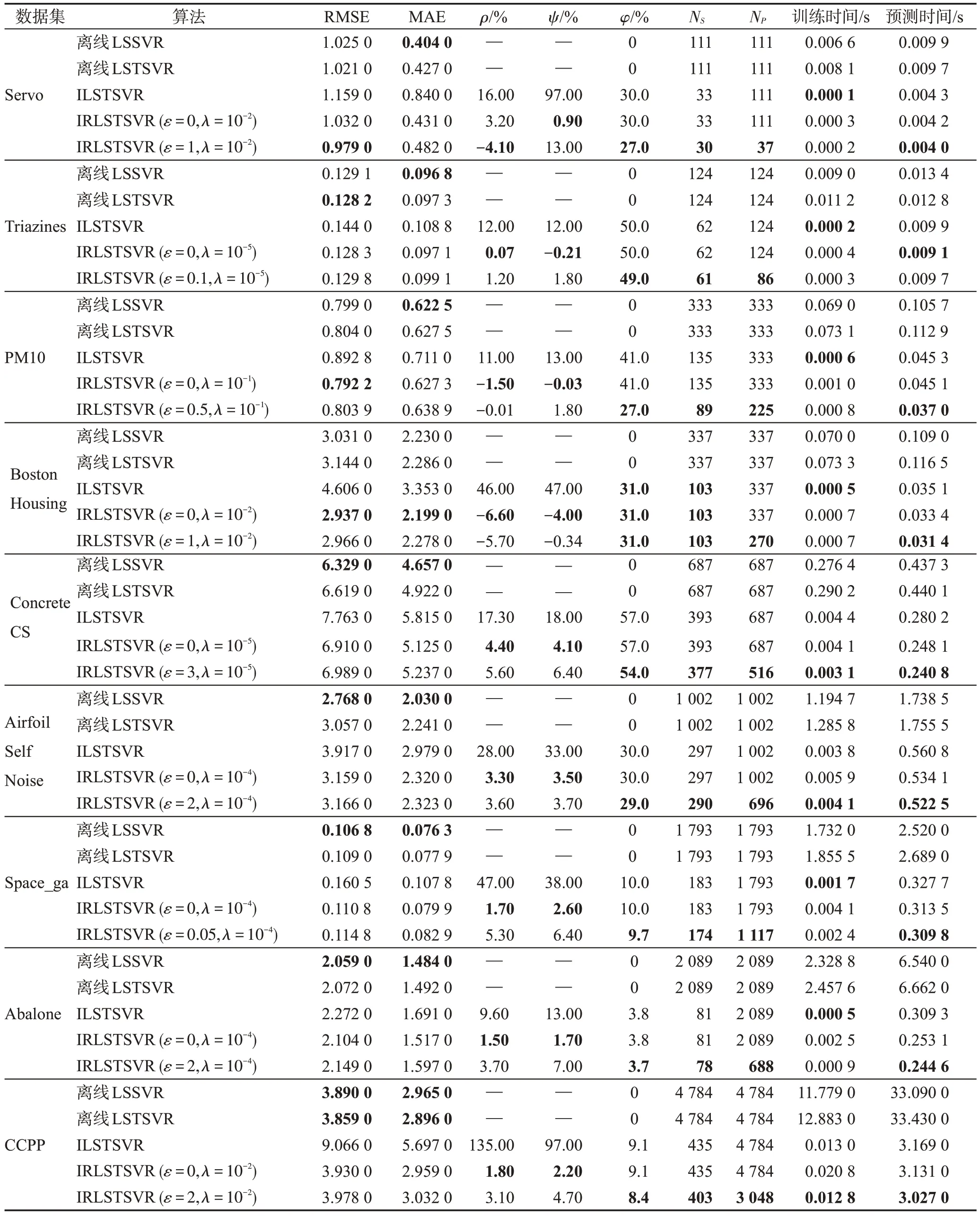
Table 2 Experimental results of four different algorithms on benchmark datasets表2 四种不同算法在基准数据集上的实验结果

对于本文算法，与当ε=0 时的情况相比，当ε≠0 时，P集合的个数减少，也就意味着减少了样本的更新次数，导致平均一次增量更新的时间会减少，但由于ε1、ε2的设置使样本偏离模型有了上限，因此依然能获得相近的泛化性能。

为了更好地说明增量过程中RMSE、MAE、总训练时间三种指标的变化，图1 给出了在Abalone 数据集上，随着训练样本个数的增加，三种指标的变化过程，其中离线算法只给出最终模型的RMSE和MAE，作为增量算法的对比基准。从图1（a）和图1（b）中可以看出，本文算法在RMSE和MAE的下降趋势方面要明显优于ILSTSVR，这是因为与ILSTSVR 算法中随机选取支持向量相比，本文算法通过约简方法，在样本增加过程中，能够更有效地保留原核矩阵中的大部分信息，获得更加近似于原核矩阵的约简核矩阵；并且当ε=0 时的模型指标要略胜于当ε≠0 时的模型指标，这是由于当ε≠0 时模型允许少量的误差存在，使得参与模型更新的样本减少，模型的性能通常也会有一定的损失。

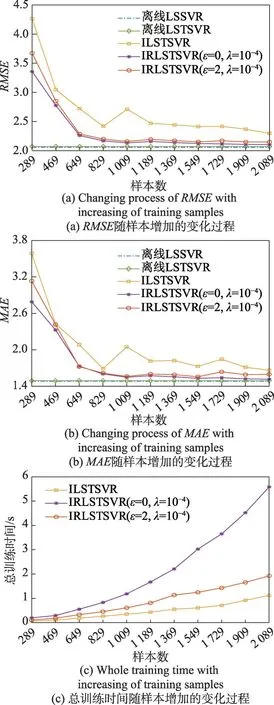
Fig.1 Performance comparison of different algorithms on Abalone dataset图1 Abalone数据集上不同算法的性能对比

从图1（c）中可以看出，ILSTSVR 算法的总训练时间要小于IRLSTSVR 算法，而且大致呈线性增长。这是由于ILSTSVR 算法每次增加样本时，仅添加核矩阵的行数，每次更新的时间复杂度是固定的。相当于每次更新仅需做2.4节所述情况2中模型解的更新部分，具体的时间复杂度为4(l1+1)2+3(l1+1)，而l1是由预训练模型提前确定的，在增量过程中不会增长，因此ILSTSVR 算法的时间复杂度要小于IRLSTSVR 算法,且总训练时间呈线性增长。而IRLSTSVR算法增加了约简过程，并且添加核矩阵列向量和行向量的时间复杂度要高于只添加行向量的时间复杂度，即2.4节中所述，情况1时的时间复杂度要高于情况2时的时间复杂度，因此本文算法的总训练时间要大于ILSTSVR 算法。而当ε≠0 时模型的总训练时间要大于当ε=0 时，原因是模型允许误差存在使得参与模型更新的样本减少，由2.4 节可知，本文算法的时间复杂度由l1、l2决定，参与模型更新的样本减少，即l2减小，总的时间复杂度也会相应地减小，也就是说参数ε能够起到控制总训练时间的作用。

4 结束语

本文结合约简孪生支持向量回归机和最小二乘孪生支持向量回归机的思想，提出了一种增量式约简最小二乘孪生支持向量回归机算法。该算法通过约简支持向量以及矩阵求逆引理，在不进行矩阵求逆的前提下，获得约简最小二乘孪生支持向量回归机模型，实现了解的稀疏化以及高效增量更新。实验结果表明，本文算法获得的模型和离线训练模型具有相近的回归精度并且能够获得稀疏解，与增量式最小二乘孪生支持向量回归机相比，泛化性能更加接近离线算法，因此本文算法具备可行性和有效性。