基于深度强化学习的船舶航线自动规划

韩志豪， 汪益兵， 张 宇， 郝永志

(1.浙江国际海运职业技术学院， 浙江 舟山 316000；2.浙江大学 舟山海洋研究中心， 浙江 舟山 316000)

随着全球信息化的不断发展，船舶智能化应用逐渐普及，在船舶航行过程中，为减少燃油消耗和降低人工成本，确保航行安全可靠，避开航行中的诸多威胁，如禁航区、锚区、浅滩和暗礁等，同时考虑船舶吃水深度、船舶拐弯半径等，设计一条航行距离较短且最安全的航线，是保证船舶安全、经济航行的关键。

航线设计需要考虑外部环境和船舶自身[1]特性。目前，航线设计有2种方式：由船舶航行专家根据风速、风向、潮汐、水生和天气等外部环境，结合吨位、吃水深度、船长、船宽、船高和拐弯半径等船舶自身特性，通过纸质海图或电子海图手动绘制航线[2]；借助电子海图仪，通过设定起点和终点，产生一条没有障碍物的最近航线，再根据外部环境、船舶自身特性和电子海图信息修正最近航线。采用这2种方式设计航线不仅非常费时费力，而且在设计时容易遗漏信息，导致船舶在航行时遇到突发状况，产生难以挽回的损失。

在研究船舶航线自动规划时，通常采用图论算法、A*算法和遗传算法，其中李擎等[3]对A*算法、遗传算法和图论算法路径规划进行比较，A*算法与遗传算法规划的航线优于图论算法，但A*算法不能结合外部环境、船舶自身特性和电子海图信息等，遗传算法收敛速度慢、易陷入局部最优。深度Q网络(Deep Q Network,DQN)算法结合深度学习与强化学习，巧妙地将深度学习的感知与表达能力融合强化学习的决策与解决问题的能力。DQN广泛应用在游戏、机器人控制、无人驾驶和机器视觉等领域中。[4]

为解决船舶航线规划算法不符合航行要求、未依航道航行和未考虑船舶自身拐弯特性等问题，本文结合电子海图信息，避开锚地、禁航区和沉船等障碍，利用DQN算法自动规划航线，确保航行的经济性和安全性。通过仿真测试验证DQN算法规划航线拟合船舶航行专家航线的可行性，结果表明，规划后的航线能依航道航行，拐弯次数较少，解决普通航线规划算法只求规避障碍的最短路线问题，且其通用性和鲁棒性较强。

1 船舶航线规划框架

利用DQN进行船舶航线规划，需先输入船舶航行专家的经验航线和该航线上的海图信息，最终目标是找到一条避开所有障碍物的航线，其规划框架见图1。

图1 DQN船舶航线规划框架

2 基于DQN的自动生成航线方法

2.1 DQN算法

基于值函数DQN算法和深度Q网络模型，该模型通过图像和地图感知并决策控制任务。Q网络是指Q-Learning强化学习算法而产生的用于决策的Q表[5]，见表1。矩阵中的An为每个动作，如航线规划中有上、下、左、右等4个动作，Sn为状态。

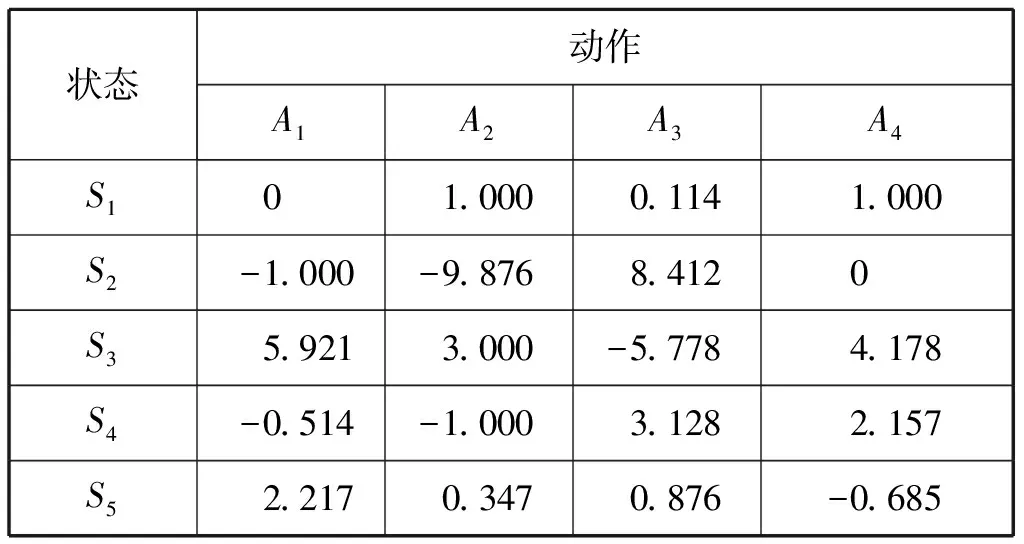
表1 用于决策的Q值表动作

表1中的Q值通过试验，反复调用式(1)进行更新，直至收敛。

Q(St,At)←Q(St,At)+α(Rt+1+

λmaxaQ(St+1,a)-Q(St,At))

(1)

式(1)中:α为学习效率且数值小于1;Rt+1为到达Q(St,At)所获得的奖励值;λ为对未来奖励的衰减值;Q(St,At)为当前在St与At上的Q值;maxaQ(St+1,a)为下一个状态St+1的最大估计Q值。

当实际问题复杂时，Q表难以承载计算维度。因此，深度Q网络模型中的深度神经网络将Q(St,At)近似等于f(s,a)，用深度神经网络表示Q(s,a,w)，在深度Q网络模型中，用2个卷积层和2个全连接层，最后输出每个动作的Q值向量，见图2[6]。

图2 DQN动作值函数逼近网络

在神经网络的最优化问题中，损失函数是标签值与网络输出的差值，目标是使损失函数最小化。[7]为达到此目标，需要大量标签数据，进而通过误差反向传播梯度下降的方法更新神经网络参数。通过Q-Learning强化学习算法，可将目标Q值作为标签，使计算出来的Q值与目标Q值形成损失函数

L(w)=E[(r+γmaxa′Q(s′,a′,w)-Q(s,a,w))2]

(2)

2.2 基于经验航线的DQN

将船舶航行专家的经验航线和电子海图数据直接用于神经网络训练数据量太大，训练速度慢，因此,将船舶航行专家的经验航线与电子海图数据图像融合，并通过颜色特征提取，将图像处理成单通道编码方式，以缩短神经网络训练时间。在进行航线规划训练时，为防止训练仅能适应熟悉电子海图场景，而不能适应陌生电子海图场景并陷入局部最优，采用批量梯度下降法加速收敛，并引入验证集，当验证集错误率不再下降时，就停止迭代。

2.2.1颜色特征提取初始化数据

由于船舶航线规划是在电子海图软件中实现的，为区分颜色，对电子海图软件的海图显示和图像渲染进行二次开发，以区分航线、航道和转向点等特征。

颜色特征提取方法是寻找某像素点与周围连续像素点之间的颜色直方图差异，只有差异大于指定阈值，才可确定该像素点与其周围像素有可识别的特征。

本文的船舶航线规划算法的环境是基于正式的电子海图，以300×300的每个像素为单位进行栅格化处理，带有陆地、沉船和障碍物。通过对电子海图进行颜色特征提取和轮廓识别后，将图像转换成单通道灰度图像，以减少训练时间，原始电子海图见图3，轮廓识别后电子海图见图4，采用红绿蓝(Red Green Blue,RGB)值为(255,0,0)标示已识别的轮廓。电子海图经验航线见图5，其中:RGB值为(0,255,0)的2×2像素点为航线的起始点;RGB值为(0,0,255)的2×2像素点为航线的终点;RGB值为(0,0,0)的为经验航线，为避免在强化学习时路径出现小范围振荡，将路径宽度设为1个像素。

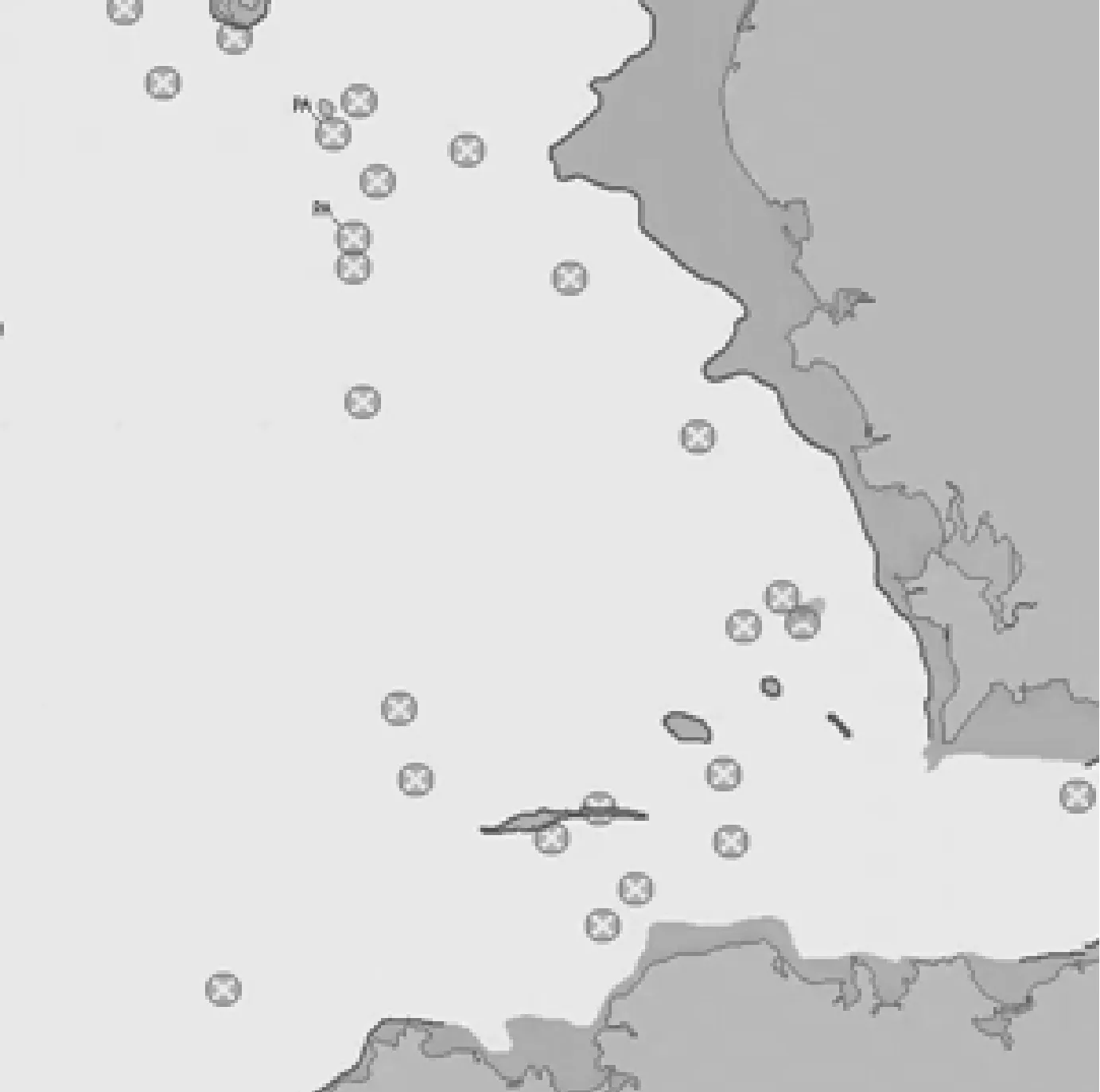
图3 原始电子海图

图4 轮廓识别后电子海图

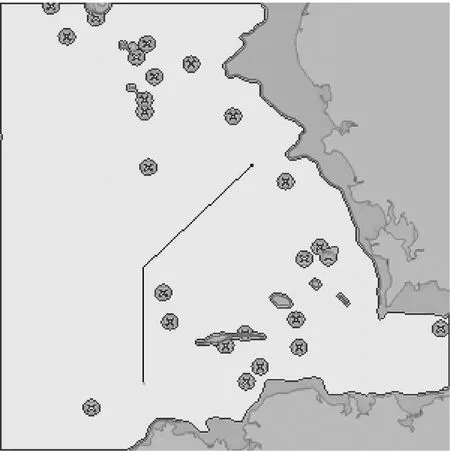
图5 电子海图经验航线

图5中浅灰色区域为可行区域，其他不规则区域为不可行区域。对于每个像素点，其上、下、左、右，左上、左下、右上和右下等8个相邻的方格为可达区域。试验目标是自动规划的航线能较好地拟合经验航线，从航线的起点到航线的终点用较少的拐弯点，并规避障碍的较短航线。在轮廓识别的电子海图中，当智能体从航线起点开始向周围点探索时，经多组奖励方案测试后，最终选定如下奖励方案，以防止陷入局部最优：遇到经验航线奖励1.0；遇到障碍奖励-0.5，结束此次周围探索；拐弯奖励-0.4；遇到终点奖励2.0，并结束周围探索。

2.2.2存储经验池和双神经网络

强化学习本身是无监督学习，强化学习算法有噪声、稀疏和延迟的奖励，而深度学习本身是监督学习，但在DQN训练[8]过程中，价值函数对动作的估计将不断优化，输出动作也逐步优化，继而影响训练样本的分布。因此，先采用存储经验池的方式存储一部分样本，然后随机采样。

本文的船舶航线规划基于船舶经验航线，在智能体Agent向上、下、左、右、左上、左下、右上和右下等8个方向探索时，采用ξ-greedy选择航行方向，ξ=0.1，即随机选择方向的概率为0.1；采用贪婪策略的概率为0.9，其中贪婪策略为

arg maxQ(st+1,a)

(3)

根据当前状态计算，试探的8个方向，并取最大的奖励方向作为下一状态航线规划的方向。通过ξ-greedy产生的经验，存储在经验池开辟的空间中，存储格式为(st,at,rt,st+1)，其中:st为当前状态;at为当前航行方向;rt为当前奖励;st+1为下一个状态。在该船舶航线规划系统中，采用2个神经网络分别作为当前神经网络和目标神经网络，二者结构相同，但数据不同，达到打乱数据间的相关性的目的。当累积经验数据至1 000步后，将当前神经网络参数拷贝至目标神经网络，之后每100步将当前神经网络参数拷贝至目标神经网络，降低当前Q值与目标Q值的相关性。当前的Q值与目标的Q值之间通过均方差更新网络参数，其误差函数为

L(θi)=Esars[(Yi-Q(s,a|θi))2]

(4)

对θ求偏导，得到的梯度为

∇θL(θi)=Esurrit[(Yi-Q(s,a|θi))∇θiQ(s,a|θi)]

(5)

通过上述方法增加数据采样次数，提高数据使用效率，同时避免从连续数据中学习效率低下、前后样本相关度高的问题。当实际训练时，也可能出现当前的参数决定最大奖励动作方向为向右，此种情况下样本多数来自右边，然后右边样本再训练，这样训练可能出现恶性循环，参数出现局部收敛，甚至发散。采用经验池的方式，数据多个状态会被平均，使训练过程平滑，避免局部收敛与发散。

2.3 基于经验航线的深度强化学习

依据第2.2.2节概述，DQN的船舶航线规划系统算法流程见图6。

在算法训练过程中，使用经验池存储当前神经网络处理得到的转移样本，有

et=(st,at,rt,s′)

(6)

在每个100步后，将智能体与电子海图环境得到的转移样本存储到经验池D={e1,…,et}中。在训练过程中，每次从经验池D中随机抽取小批量转移样本，同时采用随机梯度下降算法更新神经网络参数。

图6 DQN的船舶航线规划系统算法流程

3 试验与分析

本节介绍系统试验仿真平台测试Demo、优化参数，进而将试验参数应用于真实电子海图环境中，评估训练结果的好坏。

3.1 仿真结果分析

本文采用的基于经验航线的DQN规划船舶航线，在PC上基于Python3.6.5环境进行仿真验证。使用的Python模块包括PyQt5、tensorflow、pandas、numpy和matplotlib，模拟电子海图环境，采用广度优先搜索算法(Breadth First Search,BFS)模拟船舶经验航线，目标是通过智能体规划最接近经验航线的航线。

仿真平台首先生成10 000张10×10矩阵的地图，作为DQN的训练样本，见图7，并对每张地图生成随机障碍，用实心正方形表示；在障碍区域以外的区域，随机生成路径起始点，用正方形内嵌菱形轮廓表示；在障碍区域与起始点以外的区域，随机生成路径终点，用正方形内嵌圆形轮廓表示；用BFS生成8个方向的最短路线，模拟真实电子海图的专家经验航线，用实心三角形表示；智能体在搜索路径时，用实心圆形表示。

通过路径指引，在10 000张随机地图中，由智能体搜索每张地图的路径，损失函数的收敛速度较接近，见图8和图9，但基本在1 000次训练后，损失函数趋于0。因此,在训练时，设定每张图的训练步数为1 000步。

由于使用ξ-greedy选择航行方向，因此对于每张地图的训练步数与损失图，由随机选择方向概率带来的影响会略有不同。以示例地图2为例，当随机选择方向概率为0.5时，其训练步数与损失图见图10；当随机选择方向概率为0.9时，其训练步数与损失图见图11。随机选择方向概率越大，扰动越大，但与其损失衰减无关。

图7 深度强化学习训练随机地图

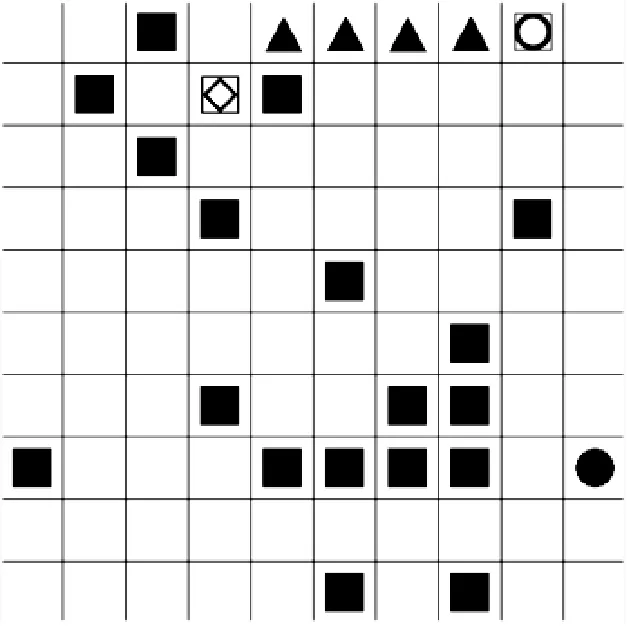
a)示例地图1 b)训练步数与损失图

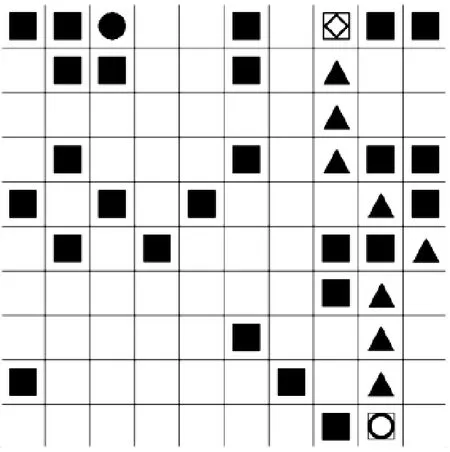
a)示例地图2 b)训练步数与频失图

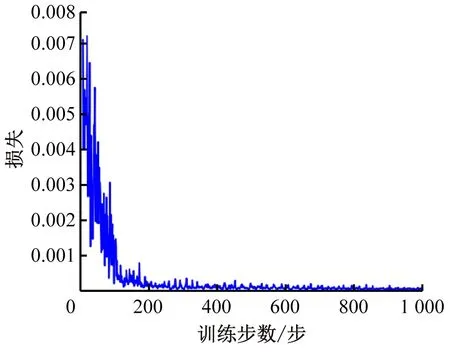
图10 示例地图2随机方向概率为0.5

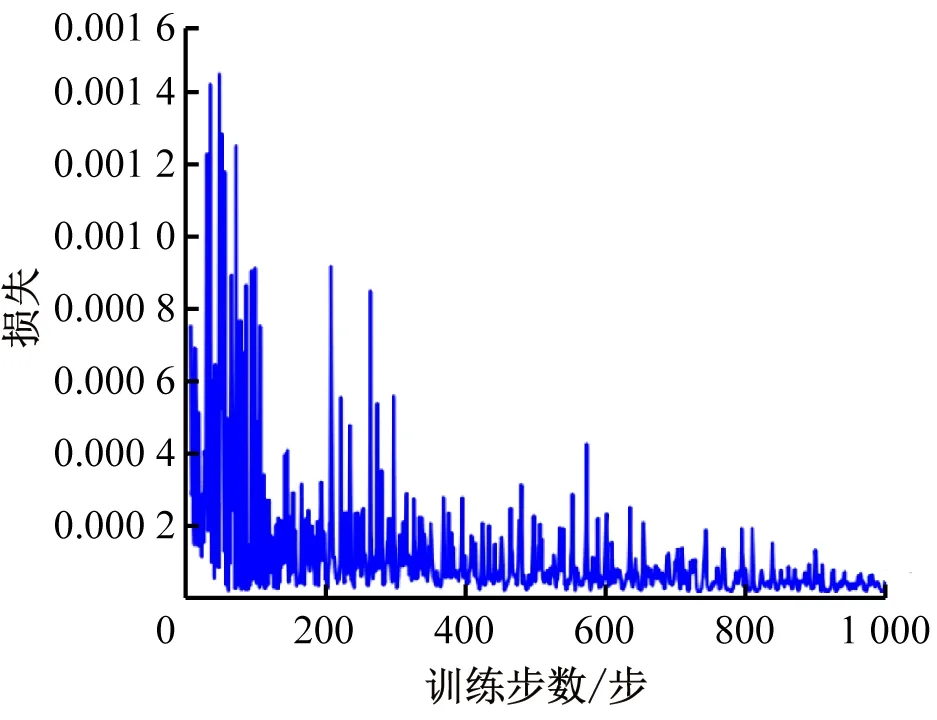
图11 示例地图2随机方向概率为0.9

当训练完成10 000张随机地图训练样本后，随机生成100张无经验航线的地图作为测试样本。测试样本生成航线与经验航线拟合率均值为71.18%，测试样本生成航线拟合经验航线概率分布图见图12。

3.2 试验结果分析

在真实电子海图系统中，采用105张经验船长规划的实际航线作为训练样本，如图5所示，经过单通道灰度处理后作为训练样本，直接输入模型中，样本为300×300像素的图像，包含起点、终点、路径、航道和障碍数据。

在训练样本时，单张图的损失与训练步数见图13。损失值收敛在400步以上，且与仿真平台相比损失值较发散。

图12 测试样本生成航线拟合经验航线概率分布图

图13 电子海图经验航线

当训练105张电子海图经验航线训练样本后，100张无经验航线的电子海图作为测试样本。测试样本生成航线与经验航线拟合率均值为65.09%，测试样本生成电子海图航线与经验航线拟合率的散点图见图14，概率分布图见图15，能基本满足基于经验航线的航线规划需求。

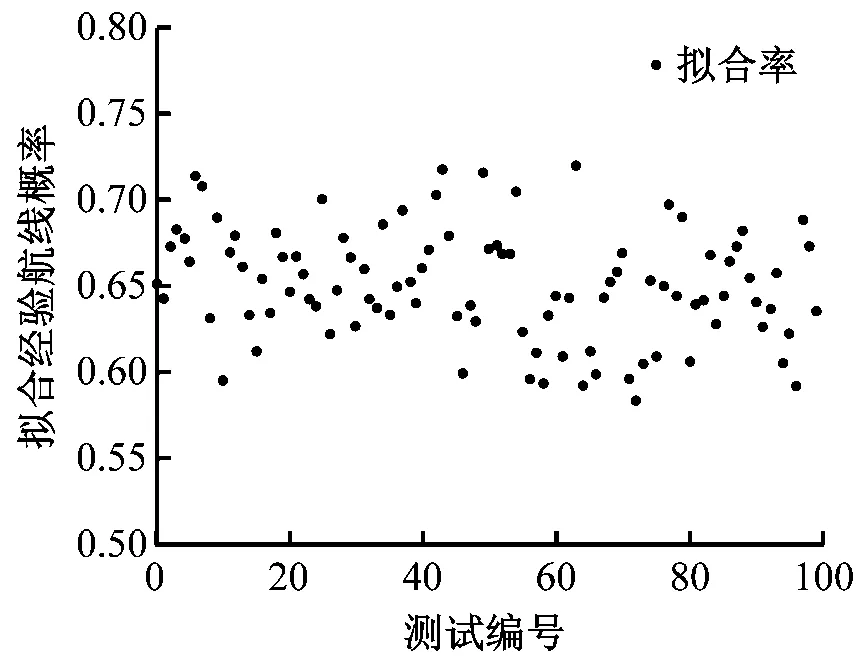
图14 电子海图测试样本拟合经验航线概率散点图

图15 电子海图测试样本

以测试样本的第71条航线为例，航线从舟山虾峙门至山野鸭山锚地，分别通过经验航线、遗传算法规划航线与DQN规划航线在电子海图上绘制航线对此见图16。虾峙门—野鸭山经验航线表见表2，总长为28.57 n mile，拐弯6次，依航道航行，用带箭头的实线表示如图16所示，依航道航行率为86.16%；A*算法规划航线见表3，总长为26.78 n mile，拐弯14次，部分依航道航行，用带箭头的点线表示如图16所示，依航道航行率为52.88%；以DQN规划航线后，自动规划航线的航点见表4，总长为27.06 n mile，拐弯5次，基本依航道航行，但未完全靠右航行，用带箭头的虚线表示如图16所示，依航道航行率为69.14%。

图16 经验航线与自动规划航线对比图

表2 虾峙门—野鸭山经验航线表

表3 虾峙门—野鸭山A*算法规划航线表

表4 虾峙门—野鸭山DQN规划航线表

4 结束语

本文提出基于经验航线的船舶航线规划方法，同时采用DQN算法，在真实的电子海图环境中实现经验航线规划功能。试验表明：DQN算法可基于经验航线进行电子海图航线规划，大大减少手动绘制航线的时间，可避免部分由于经验不足导致航线规划错误的问题，对今后基于经验航线的航线规划算法具有指导作用。本文已实现在电子海图上基于经验航线的船舶航线规划，但依航道比率还有提升空间，且数据运算效率较低，下一步将对系统参数进行优化，并将其用于实际船舶航行中。