船舶模型在波浪下的崩溃数值仿真及试验
刘维勤, 黄 宇, 王绪明, 宋学敏
(武汉理工大学 a.交通学院; b.教育部高性能船舶技术重点实验室;c.国家水运安全工程技术研究中心, 武汉 430063)
船舶在海洋中航行时会遭遇大波浪,从而导致船舶结构发生断裂,引发海损事故,造成大量的财产损失和人员伤亡。海上大波浪是真实存在的,HAYER等[1]在北海的Draupner海洋平台上监测到了极端波的存在,监测数据表明,极端波的波高可达25.63 m。KHARIF等[2]列举了1969—1994年全球因极端波导致的22起船舶事故,导致525人伤亡。MÜLLER等[3]记录挪威籍油船“威尔斯特号”在南非海域被一个极端波严重毁坏,艏部严重破损,舯部结构严重断裂。
船舶结构遭遇大波浪时的动态强度问题已引起国内外诸多学者的注意。LIU等[4]采用一个非线性的切片理论程序计算集装箱船在极端波中的波浪载荷,并将波浪载荷载入到非线性动态有限元模型中,结合静态非线性有限元计算出动态的垂向弯矩(Nertical Bending Moment, VBM)和舯部的转角。PEI等[5]提出一个结合波浪载荷与理想单元法的极限强度评估系统,可得到舯部的结构崩溃响应。PEI等[6]采用奇点分布和理想单元法分析双层底散货船在隔舱装载工况下的船体强度。目前,这些数值计算方法的有效性还没有经过试验验证。LIU等[7]进行了单波下的屈曲铰船模试验,研究极端单波下的船体结构崩溃响应和舯部的大变形,但缺乏相应的数值计算。XU等[8]设计了一个水弹塑性模型试验,将塑性铰连接2个船体,得到波浪的遭遇弯矩与极限强度的关系,但在试验中并未考虑波击或砰击产生的振动影响。
目前,研究波浪下船体结构的非线性强度的可行数值计算方法是将波浪载荷与船体强度分开计算,计算时调用波浪载荷求解器和非线性有限元2个求解器,忽略惯性力和动态效应对船体结构强度的影响。本文提出结合三维势流理论波浪载荷求解器AQWA和非线性动态有限元法求解器MECHANICAL研究船舶结构在波浪下的非线性动态强度。先采用AQWA计算作用在船体湿表面上的水动压力、船舶运动和惯性力,再将湿表面上的水动压力和船体运动引起的惯性力施加到结构有限元模型上,最后采用MECHANICAL求解船体结构的非线性动态强度。为验证该数值仿真方法的准确性和可靠性,设计一个能在试验水池条件下产生崩溃响应的船体模型,并在水池波浪下对该模型进行崩溃试验,经过模型试验验证的数值仿真方法可用于评估船体结构的非线性动态强度。
1 船体结构的水弹塑性试验设计
1.1 水弹塑性试验模型设计
模型试验是研究波浪载荷作用下船体结构崩溃响应的可行方法。
1)实船结构的崩溃需遭遇真实的海洋极端波,极端波的出现为小概率事件,具有随机性、瞬时性和不可预测性。
2)由于水池所造波浪的波高过小,普通缩尺比的试验模型拥有较大的刚度,难以在水池波浪下产生结构崩溃响应,因此,需设计一个特殊的船体模型研究船体结构在波浪作用下的崩溃行为。
船舶在波浪中航行时,舯部遭受的波浪弯矩最大,最有可能发生崩溃破坏。因此,崩溃试验模型设计为强-弱-强的改良形式。本文的船舶模型与文献[7]采用的模型相似,见图1和图2,试验模型由舯部区域用铝合金制造的屈曲铰构件和左右两端由玻璃钢制造的船体分段组成,左右两端由玻璃钢制造的船体分段的刚度很大,试验中不会产生任何变形,可视为刚体。舯部采用铝合金材料(杨氏模量E=69 GPa, 泊松比ν=0.3, 屈服强度σY=120 MPa)制造的屈曲铰构件刚度较小,在水池波浪下能产生结构崩溃响应。该屈曲铰构件不完全释放左右刚性船体的转动,可实现对船体梁结构弹塑性特征的模拟,试验时可通过测量左右两端刚性船体分段的转角变化反映舯部屈曲铰构件的大变形响应。

图1 屈曲铰构件

图2 试验模型
屈曲铰构件如图1所示,其纵向长度为100 mm,两端是直径为100 mm、厚度为10 mm的铝盘,2个铝盘由上下2个具有一定厚度的铝片相连,其中上铝片要比下铝片窄且薄,符合船舶上部结构要比下部结构更容易破坏的结构特点。屈曲铰左右两端的铝盘上设计4个螺丝孔,螺栓通过这些螺丝孔将舯部的屈曲铰构件与左右2部分刚性船体分段紧固连接,形成完整的水弹塑性试验模型。
2个船体分段为方驳状的理想形状,分别称为船体分段1和船体分段2,2个船体分段除了通过舯部的屈曲铰连接以外,还向舯部延伸的重叠区域分别设置了开孔,利用直径略小于开孔的螺栓串接船体分段1和船体分段2,从而在舯部形成理想的铰接方式,以消除屈曲铰的挤压和剪切变形,仅保留弯曲变形。每个船体分段有3个隔舱,每个隔舱的空间用来放置传感器和压载。试验模型的主尺度见表1。
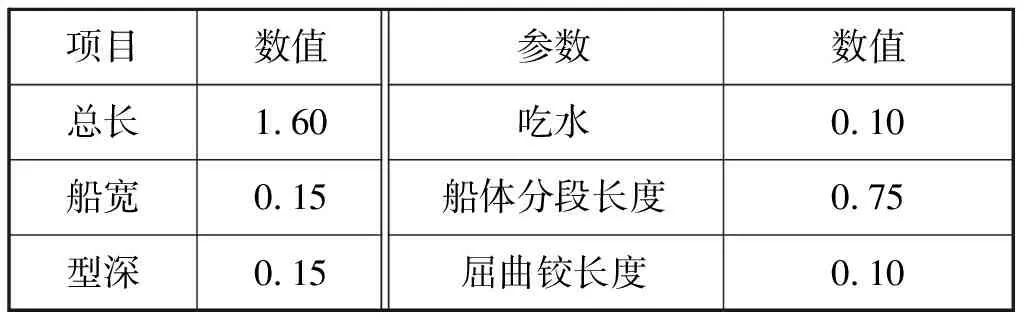
表1 试验模型的主尺度 m
通过测试2个船体分段之间的转角变形反映船舶模型在波浪下的大变形响应。为获得动态的转角变形,在2个船体分段的中间隔舱内放置无线动态倾角仪,分别命名为1号无线倾角仪和2号无线倾角仪,见图3。该无线倾角仪由德国制造,量程为±30°,测量精度为0.025°。采用无线接收器接收无线倾角仪发出的信号,并将其传输到电脑端进行试验数据记录,1号倾角仪记录的数据记为θ1,2号倾角仪记录的数据记为θ2,2台无线倾角仪记录的数据之差θb为试验模型的转角变形,即
θb=θ1-θ2
(1)

图3 测试仪器布置剖视图
1.2 波浪模型和试验工况设计
试验在武汉理工大学交通学院流体实验室玻璃水槽内进行(见图4),该波浪水槽装备的造波机可造出满足本文要求的规则波浪。SHI等[9]和LIU等[10]的研究结果表明:当波高相同,波长接近或等于1倍船长时,舯部会产生最大的变形和弯矩,本文波长取1倍模型长度,通过改变波高定义不同的试验工况,模型试验工况见表2。

图4 波浪玻璃水槽
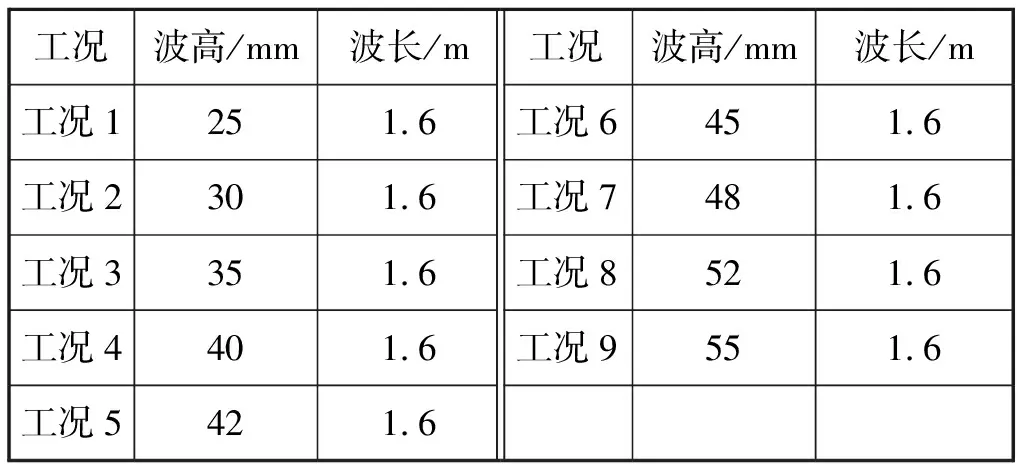
表2 模型试验工况
塑形累积影响结构的载荷位移关系,为排除塑形累积的影响,本文仅研究造波稳定后第一个规则波周期内船体结构的崩溃响应。试验中在艏部布置1台波高仪,可获得波面升高的时程曲线,工况2、工况4和工况7的波面时程曲线见图5。
1.3 屈曲铰的极限强度试验及数值仿真计算
在开展水弹塑性试验之前,先了解屈曲铰构件的极限承载能力。通过4点弯曲试验和非线性有限元方法获取屈曲铰构件的极限承载能力和载荷位移曲线。屈曲铰构件的4点弯曲试验示意见图6,屈曲铰和两端的刚性延伸段通过螺栓固定在一起,支撑屈曲铰的圆撑穿过延伸段靠近中部的圆孔,以保证屈曲铰和延伸段可绕圆撑转动。通过在延伸段左右两端的托盘上增加质量块,向屈曲铰施加垂向弯矩载荷;试验时采用百分表和拉力传感器分别记录垂向位移和拉力值,通过简单的数学变换便可得到屈曲铰的极限弯矩和载荷位移曲线。屈曲铰的极限强度数值计算在ABAQUS中进行。屈曲铰构件的转角-垂向弯矩曲线见图7,试验和数值仿真时屈曲铰构件的失效模式见图8。
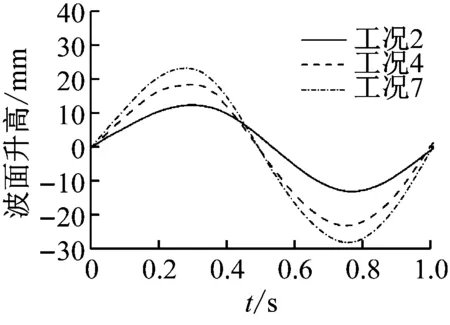
图5 工况2、工况4和工况7的波面时程曲线
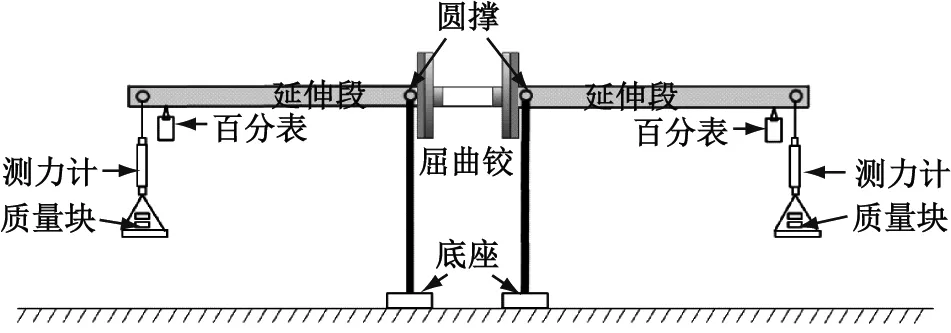
图6 屈曲铰构件的4点弯曲试验示意

图7 屈曲铰构件的转角弯矩曲线


图8 屈曲铰失效模式
屈曲铰构件4点弯曲试验和数值仿真计算的极限承载能力见表3。由表3可知:屈曲铰的极限弯矩试验值与非线性有限元计算值相差不大,利用数值方法计算屈曲铰构件的极限强度是可行的。

表3 屈曲铰极限强度点的极限弯矩和转角
2 船体结构非线性动态强度数值仿真
本文提出一种结合三维势流理论和非线性动态有限元的数值仿真方法研究船体结构在波浪作用下的非线性动态强度,数值仿真计算在ANSYS中进行,需调用AQWA和MECHANICAL进行求解计算。数值仿真分析思路见图9。
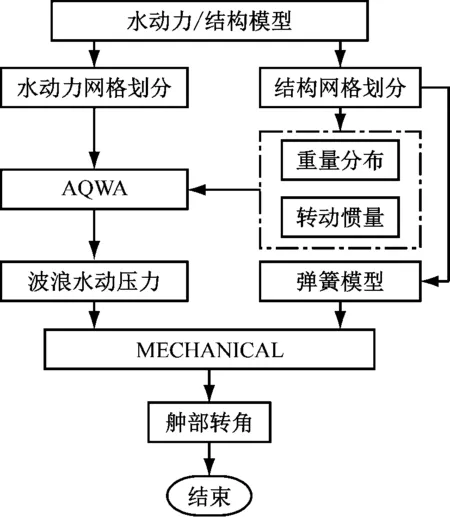
图9 数值仿真分析思路
1)建立数值计算模型。根据模型试验的详细尺寸数据建立水动力模型和船体有限元模型。水动力网格模型见图10,包含5 894个单元。结构网格模型见图11,与模型试验一致,由左、中、右3部分组成,考虑数值计算精度,对屈曲铰部分进行网格细化,屈曲铰部分包含10 184个单元,整个结构网格模型共包含30 750个单元。

图10 水动力网格模型

图11 结构网格模型
2)结构预计算。在MECHANICAL中进行静态结构预计算,提取结构有限元模型的转动惯量和重心高度等信息。
3)波浪载荷求解。提取结构预计算的转动惯量和重心高度等信息并将其输入AQWA中。
4)结构非线性动态强度计算。先在动态强度求解器中设置系列约束,实现对模型试验中各种约束的模拟;在左、右2个刚性部分的底部施加弹簧约束,模拟重力和静水力的耦合效应;在左、右2个刚性部分和屈曲铰部分之间施加设置绑定约束实现对螺栓固定的模拟;在舯部左、右个刚性部分重叠处设置铰接约束,实现对铰接约束的模拟。随后将步骤3)求解的波浪载荷传递到结构网格模型中,对波浪载荷作用下的非线性动态强度进行求解。
3 模型试验及数值仿真结果分析
3.1 船体舯部的时域转角变形对比分析
试验开始之前,分别在试验模型两端的隔舱中布置1台无线倾角仪,记录试验模型的2个船体分段在规则波下的纵向倾角运动,2个船体分段之间的倾角运动之差便是试验船体结构舯部屈曲铰的转角变形。通过模型试验和数值仿真计算获得不同波高下屈曲铰的动态转角变形,规则波的波浪载荷输入频率在低频范围内,因此由波浪载荷引起的船体遭遇变形是一种低频响应。对由试验测量直接得到的舯部动态转角变形进行低通滤波,可得到波浪载荷导致的低频船中遭遇变形,过滤掉高频颤振部分,这与数值仿真计算相符。工况1、工况2、工况4、工况5、工况7和工况8下的舯部时域转角变化曲线见图12。
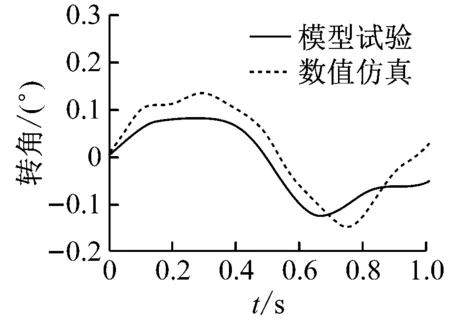
a)工况1时域转角曲线b)工况2时域转角曲线
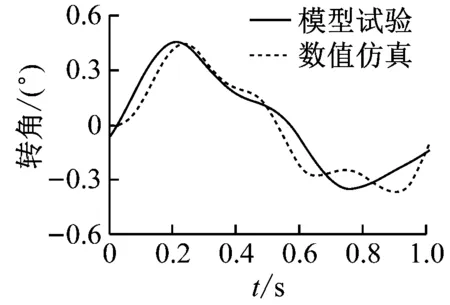
c)工况4时域转角曲线d)工况5时域转角曲线

e)工况7时域转角曲线f)工况8时域转角曲线
由图12a和图12b可知:工况1和工况2下中垂时最大的舯部转角Rs大于极限强度对应的转角θs,中拱时最大舯部转角Rh小于极限强度对应的转角θh,表明船体结构在中垂时已进入极限强度,而在中拱时处于弹塑性变形阶段,还未进入极限强度。由图12c和图12d可知:中垂和中拱时最大转角变形R已接近甚至超过极限强度对应的转角θ,这表明在这2个波高下,船体结构不论是遭遇中垂变形,还是中拱变形,都已接近甚至进入极限强度阶段。由图12e和图12f可知:中垂和中拱时最大转角变形R已大大超过极限强度对应的转角θ,这表明在此波高下船体结构已产生塑性大变形。由图12a~图12f可知:舯部时域转角变形并不是严格按照图5所示波面升高的形式变化的,不仅船体结构的中垂和中拱强度不同,而且在试验和数值计算中产生舯部大变形,是由船体结构产生崩溃变形导致的。工况7中船体处于中拱时的运动和变形对比见图13。

a)水动力数值模型

b)船体崩溃试验模型

c)非线性有限元模型
3.2 舯部的时域非线性弯矩对比分析
船体结构在波浪载荷作用下达到极限强度,此时有必要研究舯垂向弯矩,了解船体结构的承载能力的变化。屈曲铰的载荷位移曲线反映屈曲铰的非线性弯矩与转角之间的关系,第1.3节通过屈曲铰的4点弯曲试验验证采用非线性有限元法计算屈曲铰极限强度的可靠性,得到屈曲铰的载荷位移曲线,并通过模型崩溃试验得到舯部时域转角曲线。因此,通过屈曲铰的载荷位移曲线舯部的时域转角曲线进行转化,可得到船体结构的时域垂向弯矩曲线工况1、工况2、工况4、工况5、工况7和工况8下的舯部时域垂向弯矩变化曲线见图14。

a)工况1时域VBM曲线b)工况2时域VBM曲线

c)工况4时域VBM曲线d)工况5时域VBM曲线
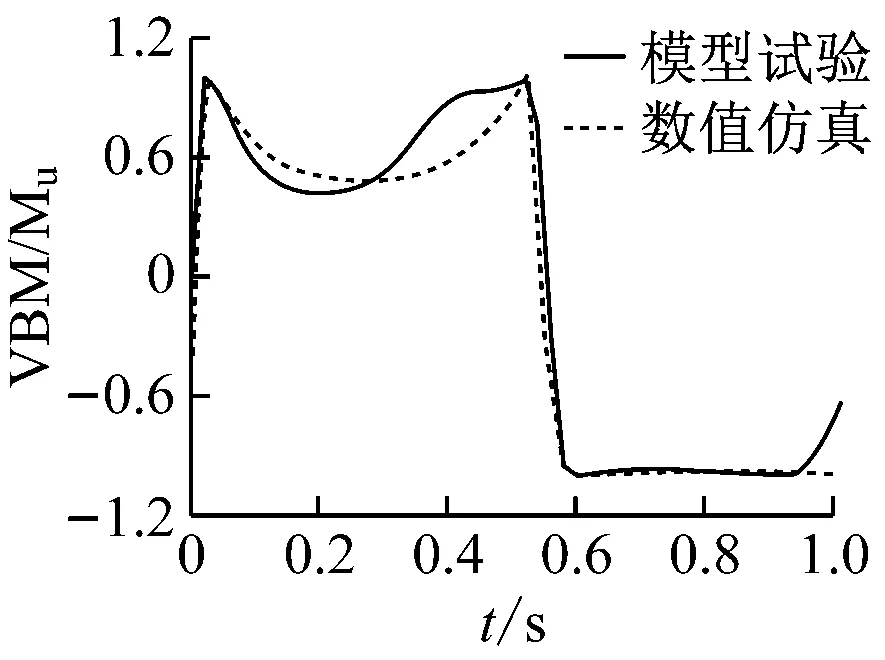
e)工况7时域VBM曲线f)工况8时域VBM曲线
利用最大垂向弯矩与极限弯矩的比值VBM/Mu评估船体结构是否还能继续承受外载荷。若VBM/Mu<1,表明船体结构还未达到极限强度状态,船体结构还具有一定的承载能力,VBM/Mu的值越小,说明船体结构的富余强度越足,可继续承受的外载荷越大;若VBM/Mu的值接近甚至等于1,表明船体结构达到极限承载状态,增大外载荷会导致船体结构崩溃,承载能力下降。由图14a和图14b可知:中垂状态下的最大垂向弯矩与中垂极限弯矩的比值VBM/Mu接近于1,而中拱状态下的最大垂向弯矩与中拱极限弯矩的比值约为0.6,表明船体在中拱受力状态下还有一定的承载能力,而在中垂状态下已接近其所能承载的最大外载荷。图14c和图14f可知:VBM/Mu的值已接近甚至等于1,无论是处于中垂状态,还是处于中拱状态,都已达到船体结构的极限承载状态。
3.3 改变波高对船体结构强度的影响
随着规则波的波高增加,对所有工况下的舯部最大转角变形和中拱状态下VBM/Mu的值进行综合分析。舯部最大转角随着波高增加的变化曲线见图15,中拱时VBM/Mu最大值随着波高增加的变化曲线见图16。由图15和图16可知:船体结构的遭遇转角变形和垂向弯矩随着波高的增加呈非线性增加,表明波高对波浪载荷和遭遇变形有显著的影响。

图15 肿部最大转角随波高的变化曲线

图16 中拱时VBM/Mu最大值随波高的变化曲线
4 结束语
本文提出一种结合三维势流理论和非线性动态有限元的数值仿真方法,研究船体模型结构在波浪作用下的非线性动态强度,同时,设计并开展一个水池波浪下的船体结构模型崩溃试验,试验结果用来修正和改进提出的数值仿真方法。通过对船体结构的模型崩溃试验结果和数值仿真结果进行分析,得到以下结论:
1)该模型试验方案能产生水池波浪下的结构崩溃响应。
2)数值仿真结果与试验结果吻合度较好,表明提出的数值仿真方法可用于评估船体结构在波浪下的非线性动态强度。
3)舯部转角变形随着波高的增加呈现出非线性增长的趋势,船体结构在大波高条件下进入结构非线性,甚至达到极限强度的状态,说明本文设计的船体结构模型崩溃试验模型可在水池波浪条件下发生崩溃。
今后可将该数值仿真方法用于工程化应用,评估实船结构在波浪作用下的非线性动态强度。

