基于历史航次信息的船舶典型轨迹

张进峰， 朱学秀， 彭斯杨

(武汉理工大学 a.航运学院； b.国家水运安全工程技术研究中心；c.内河航运技术湖北省重点实验室， 湖北 武汉 430063)

为响应“交通运输部办公厅关于印发推进智慧交通发展行动计划(2017—2020年)的通知”的要求，确保智能化运输装备升级改造任务的顺利完成，在航运方面，需加快“智能船舶”的研制力度；在船舶导航领域，通过一定的方法对在特定区域内船舶历史航次信息进行分析，得到区域内船舶的典型轨迹，可为船舶自动导航决策系统提供充分满足航行经验和航行需求的航行解决方案，以大大提高智能船舶在导航方面自动感知、自动记忆、自动学习、自动决策和自适应的能力。同时，船舶典型轨迹的获取，可帮助检测轨迹异常的船舶，有利于提高海事监管效率，进而更大程度地降低安全事故发生的可能性，保障智能船舶的航行安全以及海上人员的生命和财产安全。

获取船舶运动典型轨迹的方法大多基于挖掘技术下的轨迹聚类[1-2]，其主要研究方向可分为2类：将轨迹作为整体来进行[3-4]，该类方法能对轨迹间的相似性进行直观评估，对输入数据的要求不高，但易忽略复杂轨迹的局部异常信息;借鉴空中交通领域对历史航迹进行划分的方法[5-6]，一般通过轨迹相似度[7-10]识别轨迹特征并划分轨迹，再根据相应的轨迹片段来进行轨迹聚类[11-13]，该方法能更好地识别局部轨迹特征。为优化以上算法，牟军敏等[14]提出一种综合两类聚类算法优点的快速自适应谱聚类算法。但上述通过轨迹聚类获取的典型轨迹仅能展示出轨迹的形状，而对典型轨迹在指导船舶航行方面的考虑较少。

为使典型轨迹能对船舶导航系统有更高的指导意义，必须使典型轨迹能与船舶导航的特征相符。本文以海上交通工程为基础[15]，从为船舶导航服务的角度出发，借鉴基于划分的轨迹聚类的思路，利用在特定生产活动中，船舶起始港和目的港间的历史航次信息，对船舶产生的航次轨迹进行建模，并以遗传算法(Genetic Algorithm,GA)为基础[16]，获取起始港和目的港(将2个港口统称为目标港)间与船舶航次轨迹中船舶位置点分布规律相符的有向典型轨迹。

1 船舶航行轨迹建模

1.1 航次轨迹数据

船舶历史航次信息是由船舶运动的船舶自动识别系统(Automatic Identification System, AIS)数据与船舶水运生产活动产生的航次信息共同构成的一种含有船舶航行时间信息的轨迹数据。其中，船舶在一次生产活动中产生的运动轨迹，可称为航次轨迹，大量航次轨迹构成的数据集称为航次轨迹数据集。航次轨迹数据集中的每一条航次轨迹都包含船舶位置点、位置点的时间戳、船舶名称、出发区域信息和到达区域信息。

本文使用的历史航次信息由龙船(北京)科技有限公司提供，其由AIS数据以及与AIS数据对应的航次信息两个部分组成。

为获取相应港口间的船舶典型轨迹，须将目标港间的轨迹数据提取出来。提取轨迹数据的流程如下：

1)选取本研究中的起始港Pdep及目的港Parr，删除历史航次数据中起始港及目的港与之不符的航次信息。

2)在航次信息(简称数据集2)中提取船舶水上移动通信标识码(Maritime Mobile Service Identify,MMSI)码，找出AIS数据(简称数据集1)中与之对应的船舶。

3)在数据集1分别提取步骤1)中船舶的离港时间Ts1和到港时间Ts2。

4)截取数据集1中对应船舶Ts1到Ts2间所有位置点作为船舶的一条完整航次轨迹。

5)重复以上步骤，将所有航次轨迹汇集到一个集合中，记作航次轨迹数据集φ。

1.2 时间归一化

由于获取船舶运动的典型轨迹仅涉及到轨迹数据集的空间维度信息，因此，需通过航次轨迹数据集的时间归一化处理使后续操作忽略船舶位置的原始时间戳。

时间归一化将重写航次轨迹数据集中每艘船舶轨迹位置的时间戳，使船舶从航行开始以来经过的时间与船舶行驶的距离成正比，且船舶的总航行时间为一个固定值。

对于特定拥有m个船舶位置点的船舶航次轨迹G，时间戳可按时间顺序为

T=[T0，T1，…，Tn-1]

(1)

目标港间的固定航程记作D，任意2个相邻的位置x与y之间的航程为记作voyage(Tx，Ty)，根据式(2)设置轨迹G中任意船舶位置点i在时间归一化操作后其船舶位置的时间戳ti为

(2)

式(2)中:length(Pk-1，Pk)为点Pk-1与点Pk间的笛卡尔距离，用于描述两点间的距离。

1.3 船舶航行轨迹建模

一般情况，目标港间的航线可分为多个首尾相连的航路段，首个航路段起点为起始港位置，最后一个航路段终点为目的港位置。各航路段首尾交接的端点为航路点，当船舶行驶到航路点时，会根据航行需求改变船舶的航行参数，如航速、航向等。因此，轨迹建模可看作在海洋表面上搜索一系列的位移，海平面上的每个航路点使用其地理位置的经纬度坐标(lat，lon)进行标记。

当船舶从航路点P(latP，lonP),航行到航路点Q(latQ，lonQ)，该船舶位移矢量为

w=PQ=(Δlat,Δlon)

(3)

故有m个航路点的船舶航行轨迹R为

R=[w1,w2,…,wn]

(4)

位移矢量的经纬度变化设有相同最大值，以限制每个航路段船舶位移的幅度。

综上所述，出发点位于Pdep的轨迹可被描述为从点Pdep出发的轨迹R，其中：

R=[w1,w2,…,wn]=[(Δlat1,Δlon1),

(Δlat2,Δlon2),…,(Δlatn,Δlonn)]

(5)

航次轨迹数据集包含船舶位置所属的时间戳信息，因此，为便于对轨迹数据集进行分割(参见第2.1节)，需为轨迹数据集添加时间信息。

对于数据集中紧邻的船舶位置点1和船舶位置点2，其所构成的段S为

S=(P1,P2)

(6)

船舶在实际航行中沿该段航行的时间间隔为

Δts=t2-t1

(7)

与之类似，对于典型轨迹的候选轨迹，可用式(2)求取船舶航行的时间戳。当船舶从出发点Pdep于t=t0时出发，并执行相应的位移，即可得到船舶典型轨迹的航路段，将其各航路点表示为

[W0,W1,…,Wn]

(8)

任一航路段Si为

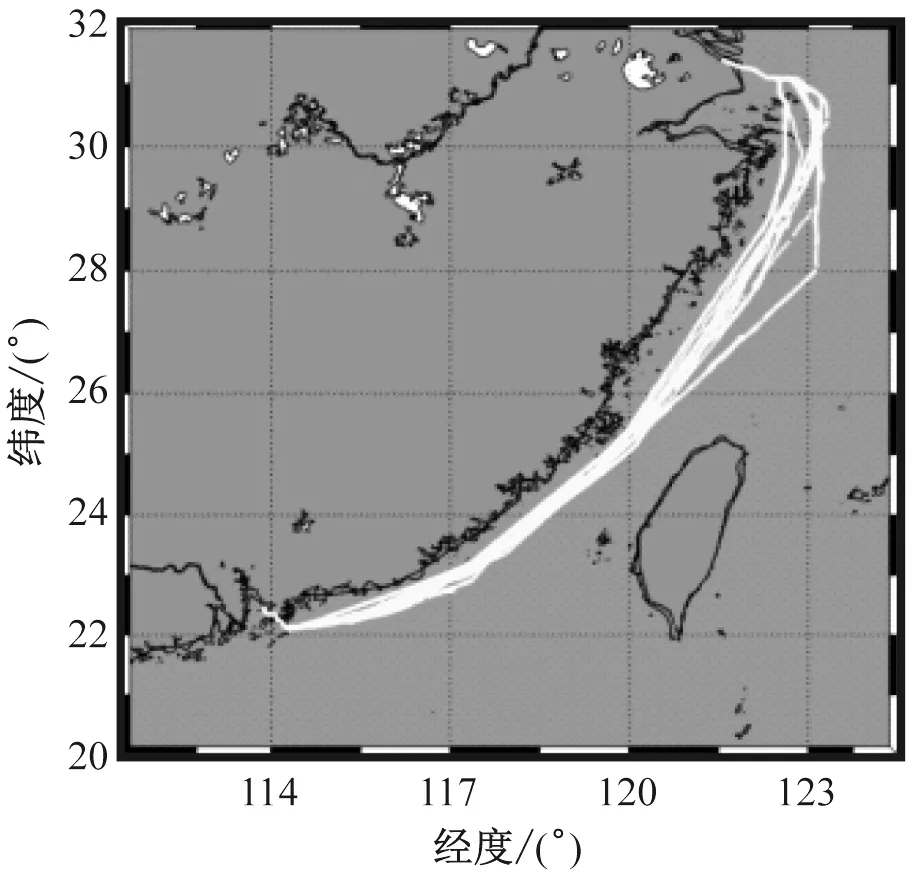
Si=(Wi-1,Wi)， 0

(9)

式(9)中：

Wi=(ti,lati,loni),W0=(t0,latdep,londep),

Wn=(tn,latarr,lonarr)

(10)

所有数据集中航次轨迹中位置点以及预设基准轨迹和候选轨迹的航路点都以式(10)的形式表示。

据此，候选轨迹可标记为

D=[S0,S1,…,Sn]

(11)

其总长度为

(12)

式(12)中：

length(Si)=length(Wi-1,Wi)=|wi|

(13)

由式(2)可知候选轨迹时间戳的计算方法为

(14)

其航行时间为

ΔtD=tn-t0

(15)

式(15)中：由于出发点Pdep处的时间戳t0=0，故ΔtD=tn。

2 轨迹参数

本文基于GA获取典型轨迹的过程需通过预设基准轨迹进行。基准轨迹是一条出发点已确定的随机轨迹，对起始港A和目的港B而言，当预设基准轨迹的出发点位于A时，则代表本文获取的典型轨迹由A指向B。在获取典型轨迹的过程中，预设基准轨迹会和GA随机生成的同类型的初始轨迹，一起作为典型轨迹的候选轨迹参与到进化中。因此,基准轨迹在GA运行前指代预设基准轨迹，运行后指代典型轨迹的候选轨迹。由于基准轨迹位移向量的数量已知，故典型轨迹航路点和航路段的数量已确定。

基准轨迹是计算轨迹参数的基准，通过GA进行进化的每一条候选轨迹都将依次成为计算轨迹参数的基准轨迹，然后用这些轨迹参数计算适应度函数值来评判候选轨迹是否是船舶运动的典型轨迹。

2.1 船舶位置点到基准轨迹的平均距离

轨迹数据集中所有船舶位置点到含有n个航路点的基准轨迹的平均距离的求取步骤如下：

1)根据基准轨迹数量，将轨迹数据集所有位置点分为n个子集，每个子集中的所有船舶位置作为两个港口间航线的一个航路段。

2)分别计算每个航路段内各船舶位置到其所在航道段部分基准轨迹的垂直距离。

3)计算每个航路段垂直距离的平均值。

4)计算每个航路段垂直距离平均值的平均值。

步骤1)中轨迹数据集的分割基于船舶位置的时间戳，当船舶进入航路段后，船舶的航速和航向均保持不变，其航程仅与航行时间有关。针对基准轨迹的航路段Si，对应基准轨迹的航路点Wi-1与航路点Wi间第i个航路段和轨迹数据集子集φi，在航路段内任意船舶位置点P均满足以下条件：

ti-1

(16)

式(16)中：tP为船舶位置点P时间戳;ti-1和ti分别为基准轨迹航路点Wi-1和航路点Wi处的时间戳。故航次轨迹数据集φ可被精确分为与基准轨迹航段数量n相同，且互不相交n个子集φi(0

轨迹数据集分割的分段示例见图1。

图1 轨迹数据集分割的分段示例

对于船舶位置点P，其到基准轨迹垂直距离d为点P和经过点P且垂直于基准轨迹航路段的直线与基准轨迹航路段交点的两点间的笛卡尔距离。

(17)

2.2 轨迹到目的港的距离

由于典型轨迹的最后一个航路点即第n个航路点为轨迹终点，因此，需评估基准轨迹到目的港的距离。这项参数与航次轨迹数据无关，只取决于基准轨迹末尾的位置。具有n个航路段的基准轨迹的第n个航路点为Wn，其距固定的目的地Parr的距离为

D=length(Wn,Parr)

(18)

2.3 平均航向变化

船舶在沿轨迹航行时，可能会在航路点改变其航向。因此，船舶航向变化定义为船舶在航路点前一航路段的航向与后一航路段航向的差值的绝对值。

对于轨迹中任意航路点Wi，其前后两端航路段分别为Si和Si+1，其航向分别为Ci和Ci+1，则船舶在航路点Wi处的平均航向变化为ΔCi为

ΔCi=|Ci+1-Ci|,0

(19)

由式(19)可知：在航向变化仅受航向改变幅度的影响，而与航向改变的方向无关。

故n个航路段的轨迹的平均航向变化为

(20)

3 典型轨迹求取

3.1 GA

GA是一种模拟的物种选择、育种、突变和进化过程搜索最优解的启发式算法。GA的目标是在有限的时间资源的情况下，为个体寻找对环境的最佳适应度。GA流程见图2。

图2 GA流程

为从航次轨迹集φ中求得目标港间的典型轨迹，将通过GA获得典型轨迹的船舶候选轨迹作为GA的个体，记作候选轨迹T，T的出发点全部位于起始港，航路段的数量相同且与预设基准轨迹的航路段数量一致，航路段的每个位移向量作为个体的一个基因。

T的集合为GA育种的种群，GA通过计算每条候选轨迹的轨迹参数，即可计算T的适应度，并通过选择过程选择最优个体进入下一步。

通过轨迹航道段位移向量的交叉和突变对GA的交叉和突变过程分别进行模拟，GA的交叉运算被模拟为切割某个航路段两父辈候选轨迹相同位置的位移向量，然后将两者交换，组成两个子辈候选轨迹，其中父辈候选轨迹中含有空心的轨迹部分即为发生交叉运算航路段。候选轨迹的突变是轨迹中某个航路段内的位移向量变为其他的随机位移向量，从而生成新的子轨迹，其中父辈候选轨迹中含有空心的轨迹部分即为发生突变运算航路段。

3.2 典型轨迹适应度函数

GA中适应度即为个体解决问题的能力。因GA优选出的个体是适应度最大个体，这里将候选轨迹的轨迹参数加权就和，并将此值称为候选轨迹适应度函数的目标函数为

(21)

式(21)中：fp、fD和fc为加权因数。参照第2节轨迹参数的定义，显然使适度函数的目标函数越小的候选轨迹与直达航次轨迹集内所有船舶位置点的分布规律越相符。因GA选择出的个体是适应度较高的个体，故适应度函数可取F的倒数为

(22)

4 典型轨迹实例

本文以上海港—深圳港2015年9月—2016年6月的部分船舶的历史航次信息数据为例，获取由上海港出发直达深圳港的船舶典型轨迹。经数据处理共获得了103条上海—深圳的航次轨迹。

出于船舶导航的目的，使用GA求取典型轨迹时需对航次轨迹进行分类，目的是将轨迹数据集中的非直达轨迹与直达轨迹区分开来，形成新的轨迹数据集作为GA的数据训练集，以提高典型轨迹的求取效率和精度。因篇幅有限，这里给出分类的结果，其中直达航次轨迹可记作φZ。直达航次轨迹及非直达航次轨迹见图3。

a) 直达航次轨迹

典型轨迹的求取基于直达航次轨迹数据集，对于GA的适应度函数的目标函数，根据轨迹参数的重要程度，将其取为

(23)

GA共产生100代子种群，通过对比运行各种不同的交叉概率和突变概率的GA获取的典型轨迹结果的，这里将GA的种群的个体数量设为500，交叉的概率设为0.5(50%)，突变概率设为0.2(20%)。

在多次试验反复检验试验后，将预设基准轨迹的航路点定为9个，当GA运行100代后，可获得直达典型轨迹。典型轨迹与船舶位置点的匹配图见图4a，典型轨迹的形状见图4b。

a) 典型轨迹与船舶位置点的匹配图

为使GA的优化过程更加直观，适应度函数的目标函数值的变化值见图5。

根据轨迹参数及适应度函数的定义，当适应度函数目标函数越小时，可代表候选轨迹的与船舶位置点的位置误差越小，候选轨迹的终点距终点更近且形状更平滑，适应度越高。由图5可知：GA大概在运行20代后即可大致获得最终的典型轨迹，其收敛速度很快，效果较好。

图5 适应度函数目标函数最优值变化趋势

5 结束语

本文从为船舶导航服务的角度出发，建立船舶运动轨迹模型，引入描述轨迹特征的轨迹参数，提出基于GA获取船舶运动典型轨迹的方法，主要结论如下：

1)方法能很好地从航次信息中获得船舶运动的有向典型轨迹，典型轨迹获取的结果与船舶航次轨迹中船舶位置点分布规律基本相符。

2)典型轨迹获取算法的收敛速度快，自动学习及自适应能力强，具有较高的效率。

3)从典型轨迹的结果看，还可对航次信息进行不同类型划分，如根据时间季节、航行需求(如船舶行驶过程中挂靠特定港口)等，从而获得不同类型的典型航行轨迹，从而提高典型轨迹在导航过程中的实用性。