基于预测控制的绞吸挖泥船横移过程控制系统设计

白一鸣， 王东生， 王 伟

(1.大连海事大学 船舶电气工程学院， 辽宁 大连 116026;2.中交疏浚技术装备国家工程研究中心有限公司， 上海 200082)

绞吸式挖泥船广泛应用于港口航道的建设和维护、防洪清淤以及环境改造，这类疏浚设备的发展对我国海洋强国的建设具有非常重要的意义[1]。绞吸式挖泥船主要由船体、定位桩系统、泥浆输送系统、绞刀切削系统、台车步进系统、横移系统等组成，如图1所示。

图1 绞吸挖泥船系统组成

作业过程中，挖泥船的横移速度是影响泥浆浓度的主要因素[2]。由于疏浚区域泥沙环境的复杂多变，不同的土质环境对疏浚产出的泥浆浓度影响非常大。现阶段绞吸挖泥船的横移过程控制大多处在手动操作阶段[3]。在挖泥过程中，操作人员需要频繁操作横移手柄控制横移速度，以保证挖泥船的泥浆浓度处于相对稳定状态[4]。

目前，挖泥船的研究热点在于如何自动控制横移速度，以确保泥浆稳定输出。唐建中等[5]利用专家系统控制横移速度将挖泥船稳定在某个稳定工作点。李志刚[6]基于横移阻力自动控制绞吸挖泥船的横移速度以优化泥浆输出。朱文亮等[7]研究了基于挖泥船实测数据建立横移过程模型的方法。陈秀静等[8]基于Q学习理论提出了绞吸挖泥船横移过程智能控制方法。魏长赟等[9]利用预测控制理论做了绞吸挖泥船横移过程的预测控制系统研究。以上研究很大程度的推动了挖泥船自动控制系统的发展。但针对横移过程建模中，要么过于的局限，要么过于的理想化，忽略了过多重要性能参数。因而，难以准确描述实际挖泥船疏浚过程中横移过程的动态特性，对应的控制器设计也难达到稳定输出泥浆浓度的目标。

在挖泥船横移系统建模过程中，为避免机理模型所引起的系统误差，本文基于挖泥过程中的实际数据，运用基于线性回归的系统状态空间辨识算法，建立横移过程的全局动态模型。在预测控制器的设计中，直接采用了子空间辨识方法生成的子空间预估器。当控制量有约束时，预测控制器仍能进行滚动优化和反馈校正，从而实时优化控制挖泥船横移系统运行，保证了挖泥船施工时泥浆浓度的稳定输出。

1 系统建模

由于影响绞吸挖泥船横移挖泥过程因素众多，难以用精确的数学模型描述其动态过程。本文基于绞吸挖泥船的实船采集数据，运用线性回归的状态空间辨识方法(State Space ARX with Linear Regression，ARX SSARX-LR)，以挖泥船横移速度为输入，以泥浆浓度为输出，建立绞吸挖泥船横移过程的动态模型[10-12]。

1.1 线性回归的状态空间辨识算法

1) 状态空间辨识

本文将绞吸挖泥船横移过程控制系统考虑为线性时不变离散系统，其模型采用新息形式的状态空间方程模型

xk+1=Axk+Buk+Kek

(1)

yk=Cxk+ek

(2)

式中:uk，yk，xk，ek分别是输入、输出、状态和噪声序列，其中ek为零均值白噪声。状态空间辨识问题就是利用长度为N的输入和输出数据:u0，u1，…，uN-1；y0，y1，…，yN-1，来求得该系统的状态空间方程模型的各个系数矩阵，即A，B，K，C。

2) 主方程的推导

根据方程式(1—2)，得到

(3)

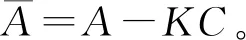
(4)

式(4)是主方程式。

3) ARX模型参数的估计

为计算式(4)的左端，需要估算式(4)的右端，也就是获得βi，φi及es+r的估计。为此，可以首先估计系统的ARX(有外部输入的自回归)模型。在这种情况下，可以基于式(2)推出下式

(5)

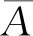
YF≈ΘWp+E

(6)

式(6)是一个典型的线性回归问题。估计θ的公式为

(7)

4) 乘积矩阵的估计

扩展能观测性矩阵定义为

(8)

式中f的选取应使得O列满秩。后面将讨论p，f的选取方法。状态序列定义为

(9)

根据主方程式(4)，可得

(10)

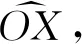
5) 状态序列的估计

(11)

式中:U，V都是正交矩阵，Σ是对角矩阵。

因此可以令

(12)

6) 乘积矩阵的估计

由式(3)和式(2)得

(13)

(14)

1.2 横移过程控制系统建模

本文基于数据挖掘理念，在对挖泥船泥浆浓度变化过程的详细分析基础上，结合横移过程的全局动态特性，利用某挖泥船实际作业数据建立横移挖泥过程的动态模型[13]。输入数据为挖泥船实船采集的横移速度，输出为挖泥船实船采集的泥浆浓度，在步进为1.2 m时，共获取了2 000组数据，数据曲线如图2所示。

a) 横移速度数据

直接基于挖泥船挖泥过程得到数据，利用上文提出的基于线性回归的状态空间辨识算法，推导出挖泥船横移挖泥过程的新息形式的状态空间方程的矩阵为

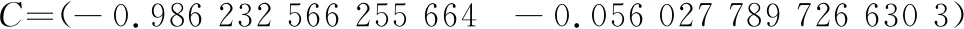
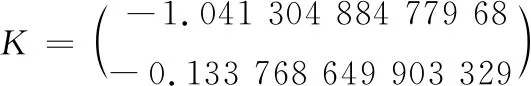
(15)

从而，建立了挖泥船横移过程的状态空间模型。为验证建模效果，当模型输入横移速度为15(m/min)时，输出量泥浆浓度能够达到稳定，效果图如图3所示。

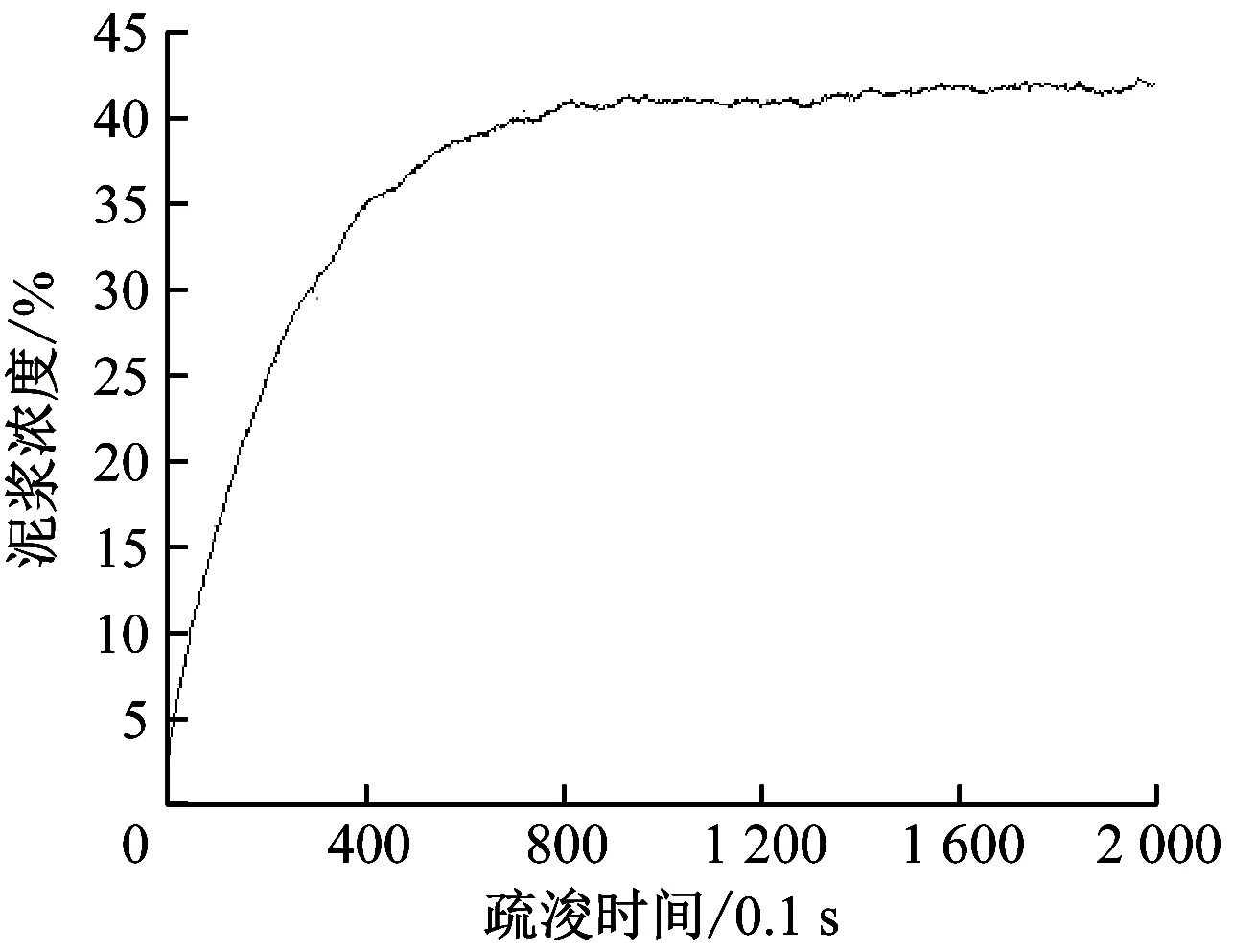
图3 泥浆浓度变化曲线

2 横移过程控制器设计

2.1 预测控制系统原理

横移过程模型能够根据当前的泥浆浓度和横移速度，预测未来泥浆浓度。然后通过预测控制策略，在浓度设定值有约束的条件下，计算出该浓度所对应的横移速度。图4为横移过程的预测控制系统结构图。

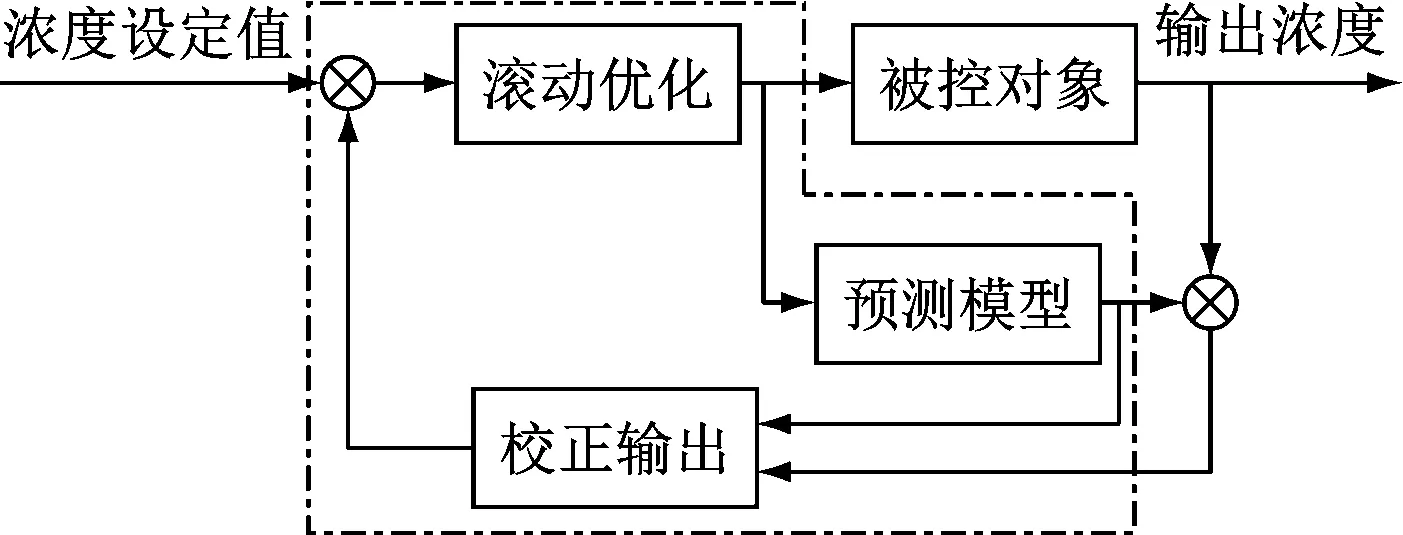
图4 横移过程预测控制系统结构图

2.2 约束预测控制算法结构

基于子空间辨识的约束预测控制算的法关键步骤主要包括：

1) 数据预处理。首先确定输入和输出数据的增量形式，用u(t)表示输入，用y(t)表示输出，然后将测量的输入和输出增量数据添加进Hankel矩阵。

2) 构造目标函数。首先对Hankel矩阵利用最小二乘算法求解Lw、Lw，通过当前时刻测量的过去的输入输出数据Wp，求解未来时刻的输出量。

3) 约束的处理。确定约束条件对控制量的影响，系统的约束一般由输入约束、输出约束以及它们的变化率约束组成。

4) 求解控制输入。在有约束条件下根据QP滚动优化目标函数，求解得到控制变量[14-16]。

2.3 子空间预估器模型

给定N个采样数，输入u∈Rm，输出y∈Rl，预测时域、控制时域为P。计算Δu(k)和Δy(k)，

Δu(k)=u(k)-u(k-1)

Δy(k)=y(k)-y(k-1)

(16)

基于此建立Hankel矩阵。

子空间预估器模型可描述如下：由过去的输入输出增量ΔWp和将来的输入ΔUf，得到将来输出增量ΔYf的预测值

(17)

其中p和f分别代表“过去”和“未来”，L=(LwLu)为子空间矩阵，可利用最小二乘问题求得：

(18)

2.4 约束的处理

典型的过程约束如下：

(19)

得到预测控制器形式：

(20)

式中

(21)

Im为m维单位矩阵，m为数据的输入的个数。Il为l维单位矩阵，l为数据的输出的个数。

为了利用未来的控制变量ΔUf来滚动优化目标函数，ΔUf的约束条件可以合并为矩阵不等式AΔUf≤b。

这样可以得到

(22)

可以在MATLAB中使用工具箱中的QP函数直接来求解ΔUf，具体形式为：

ΔUf=quadprog(H,f,A,b)

(23)

在得到适当的控制轨迹ΔUf之后，只有轨迹中的第一个值加在当前输入值上提供必要的输入将输出驱动到所需的设定值。在下一个时间步骤中(23)重复。

3 挖泥船横移过程控制系统仿真

现针对数据采集水域挖泥船的实际作业状况，在挖泥船正常施工步进距离为1.2 m时，确定控制目标为泥浆浓度维持在40%，容许泥浆浓度变化范围为±5%。

1) 基于子空间辨识的无约束预测控制器设计

期望泥浆浓度设定为40%，设定p=f=5，控制时域设定为5，误差权矩阵Q设定为1，控制权矩阵R设定为0.1。系统采样周期T为0.1 s。在Matlab中设置仿真时间为500×0.1 s，运行仿真模型图后得到控制效果图如图5所示。

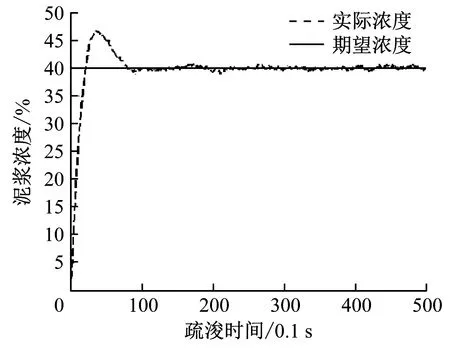
a) 泥浆浓度变化曲线

从仿真效果图可以看出，设计的基于子空间辨识的无约束预测控制器，可以有效地跟踪期望输出，其能在10 s以内使泥浆输出浓度达到稳定，具有迅速的响应速度，但超调量太大，约为40%。采用最小化二次型目标函数求解时，由于没有对输入控制量进行控制，第一次达到跟踪稳态会出现较大的超调，且横移速度瞬间过大，不符合实际的挖泥控制过程，易引起挖泥管堵塞，为此将采用基于子空间辨识的有约束预测控制算法。

2) 基于子空间辨识的有约束预测控制器设计

控制器其他参数与无约束控制器相同，在此将横移速度约束在0～20 m/min。在Matlab中设置仿真时间为1 000×0.1 s，运行仿真模型图后得到控制效果图如图6所示。

a) 泥浆浓度变化曲线

从仿真效果图可以看出，设计的有约束子空间辨识预测控制器能将挖泥船横移速度约束在0～20 m/min内，调节稳定时间大概为30 s，泥浆输出浓度几乎没有超调，更符合绞吸挖泥船的实际工作需要，泥浆稳定输出又不易造成挖泥管道堵塞。

4 结 论

本文根据挖泥船的工作原理和横移挖泥作业流程，以某绞吸挖泥船实船采集数据为基础，利用具备线性回归功能的线性系统状态空间辨识算法建立横移过程的动态模型。进而基于数据挖掘理念，利用预测控制理论，设计了针对挖泥船横移过程的泥浆浓度控制器，并对泥浆浓度控制器做了输入控制量约束。仿真结果表明，在横移速度有约束的条件下，控制器能够快速稳定泥浆浓度到目标值，从而提高挖泥船作业效率。