基于SVM与改进AHP-DS证据融合的故障诊断方法
刘利源, 孙宏林, 何治斌, 张均东
(大连海事大学 轮机工程学院, 辽宁 大连 116026)
船舶空调系统作为重要的辅助设备,能够保障船舶舱室的空气调节,为船员提供舒适的生活环境[1]。但由于船舶工作环境多变并且空调系统结构复杂,导致系统运行不稳定及故障频发,缩短设备的使用寿命,所以有必要研究性能更为优越的船舶空调系统故障诊断技术[2]。
故障诊断技术一般通过对各状态参数信息进行处理、分析,给出诊断结论,信息数据量的大小对诊断效果产生直接影响[3]。支持向量机能够在少量的训练样本中获得良好的分类识别能力,SVM与粒子群算法相结合,能够有效提升SVM的识别正确率[4]。DS证据理论能够融合证据体的基本概率分配(Basic Probability Assignment,BPA),将多源信息进行综合处理[5]。但是,大部分关于DS证据加权融合的研究缺乏严谨的理论支撑,其中证据可信度一般简化为使用各证据体的整体故障诊断精度来代替,所以需要对该环节进行加强和完善。
本文以支持向量机故障识别为基础,将层次分析法结合DS证据融合对船舶空调系统故障进行诊断。首先使用遗传算法和粒子群算法对支持向量机的惩罚系数C和核函数参数σ进行全局寻优,并将SVM模型诊断硬判决输出转化为基本概率分配。为解决传统DS证据融合仅使用冲突系数K衡量证据冲突,在高冲突证据融合过程中失效的问题,引入差异性、冲突性和不确定性3个证据冲突衡量标准,使用协方差矩阵及模糊偏好关系矩阵代替层次分析法中的两两比较矩阵,克服层次分析法中两两比较矩阵构造过程中主观性影响,构建层次结构模型获得各证据体的可信度权重,实现证据体加权融合。通过对比分析不同模型的诊断结果,验证了该方法能够有效处理高冲突证据融合问题,同时具有较高的整体故障诊断精度。
1 故障诊断基本理论
1.1 SVM理论
支持向量机通过建立一个分类超平面,使正反例的隔离边际最大化,在模式识别领域应用广泛[6]。
对于非线性可分问题,利用软间隔后,优化问题为:
(1)
其中,ξi≥0为松弛变量;C>0为惩罚因子,C越大对于误分类的惩罚越大。
利用核函数替代原样本间的内积后,相应的分类判决函数变为:
(2)
其中,sgn(u)为符号函数;ai为拉格朗日算子;b为阈值偏差;K(xi,x)为核函数,径向基核函数公式如下:
(3)
使用遗传算法(Genetic Algorithm,GA)和粒子群算法(Particle Swarm Optimization,PSO)对SVM的惩罚因子C和核函数参数σ进行全局寻优,形成基于SVM的3个证据体,即SVM(m1)、GA-SVM(m2)和PSO-SVM(m3)。
1.2 DS证据理论
DS证据理论擅长表达并合成不确定性信息,广泛应用于多个传感器的数据融合[7]。DS证据理论主要由基本概率分配函数、信任函数和似然函数构成[8]。
假设有同一个识别框架为Θ,有两个不同的证据体的基本概率分布函数分别为m1和m2,焦元分别为A1,A2…Ak和B1,B2…Bn,定义冲突因子K如下式[9]:
(4)
其反映的是两个证据间的冲突程度,假如K<1,则对于某个命题Z,有两个证据的合成公式如下所示[10]:
(5)
2 AHP-DS证据融合
2.1 不同的冲突衡量标准
在融合过程中当证据之间存在较大冲突时会产生反直觉的结果,仅使用冲突系数K并不能有效地度量证据之间的冲突程度[11]。为了准确地衡量证据之间的冲突程度,更合理地评价证据的信度,综合考虑了影响证据之间冲突的三个标准因素:差异性、冲突性和不确定性。
1) 差异性
假设有同一个识别框架为Θ,有两个不同的证据体的基本概率分布函数分别为m1和m2,支持概率距离为[12]:
(6)
其中,支持概率距离函数为:
(7)
当有n(n>2)个证据体时,使用除mi外的n-1个证据体的平均支持概率距离来表示证据体mi的差异性,计算公式如下:
(8)
2) 冲突性
在DS证据理论中,经典的冲突度量方法是使用冲突系数k来度量证据之间的冲突。证据冲突conf(mi,mj)可以随冲突系数k单调递增,假设有同一个识别框架为Θ,有两个不同的证据体的基本概率分布函数分别为m1和m2,其证据冲突为[13]:
conf(mi,mj)=-log2(1-k)
(9)
证据体mi的冲突为:
conf(mi)=conf(mi,mE)
(10)
其中mE为除mi外的n-1个证据体的平均概率分配,定义如下:
(11)
3) 不确定性
传统的证据不确定性使用不确定区间进行确定,只考虑了m(A)、Bel(A)、Pl(A)的部分信息,不能有效地表示不确定度信息。根据信念区间的定义,最不确定的情况为[0,1]区间。假设有同一个识别框架为Θ,证据体的信念区间为[Bel(θi),Pl(θi)],使用信念区间与[0,1]区间的距离代表证据体的不确定性TU(mi)定义如下[14]:
(12)
d([Bel(θi),Pl(θi)][0,1])=
(13)
2.2 改进层次分析法
为了避免传统层次分析法中两两比较矩阵构造过程中的主观影响,根据各准则定量值之间的协方差,构造准则层的两两比较矩阵,确定准则层的权重;利用各准则定量值之间的方差构造模糊偏好关系矩阵,用模糊偏好关系矩阵代替方案层的两两比较矩阵来计算方案层的权重,将准则层和方案层的权重进行组合得到各证据的权重,从而消除主观因素的影响[11]。可信度评价的层次结构模型如图1所示。
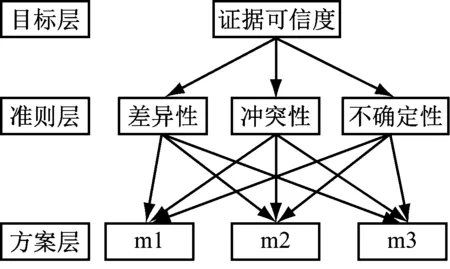
图1 可信度评价的层次结构模型
1) 准则层权重的确定:
通过各标准定量值求取协方差矩阵,并将其转化为主对角元素为1的相对协方差矩阵,通过下式可以唯一确定两两比较矩阵。
(14)
(15)
其中,aij是比较矩阵元素;bij是相对协方差矩阵元素。
2) 方案层权重的确定:
使用各度量准则下证据体间的相对方差Vi构造模糊偏好关系矩阵,该方法能够保证矩阵确定的唯一性,模糊偏好关系矩阵元素Pij如式(16)、(17)所示:
(16)
Pji=1-Pij
(17)
(18)
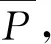
(19)
(20)
(21)
其中,rij是方案xi优于方案xj的优先级指标;Ri是方案xi在方案集合中的优先级指标;ω(mi)是方案xi的权重。
3) 各证据权重的确定
将准则层和方案层进行组合,得到各个证据的权重。
(22)
式中,ω(i)是准则层权重;ω(mi)是方案层权重。
4) 加权证据的确定
(23)
ωi是证据体权重;mi(θj)是识别框架下各证据体的基本概率分配。
本文的船舶空调系统故障诊断整体模型如图2所示。
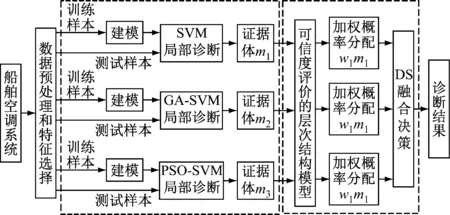
图2 故障诊断整体模型
3 实例验证
3.1 数据采集
本文使用大连海事大学实习船“育鹏轮”某次航行时的船舶空调系统正常运行数据,由于实船故障数据样本数量不足并且难以获取,所以使用根据“育鹏轮”开发的DMS动态轮机模拟器进行空调系统故障模拟试验采集故障数据。
在试验过程中采集系统运行的12个参数,分别为蒸发器蒸发压力、压缩机进、排气压力、冷凝器进气温度、冷却水进、出水温度、送风机送风温度、湿度、空气含水量、舱室空气温度、湿度、空气含水量。采样周期为10 s,每种工况模式收集了200组样本,共1 200组样本, “育鹏轮”模拟器空调系统如图3所示,工况类型和样本数如表1所示。
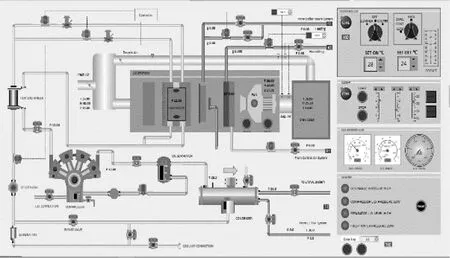
图3 “育鹏轮”模拟器空调系统
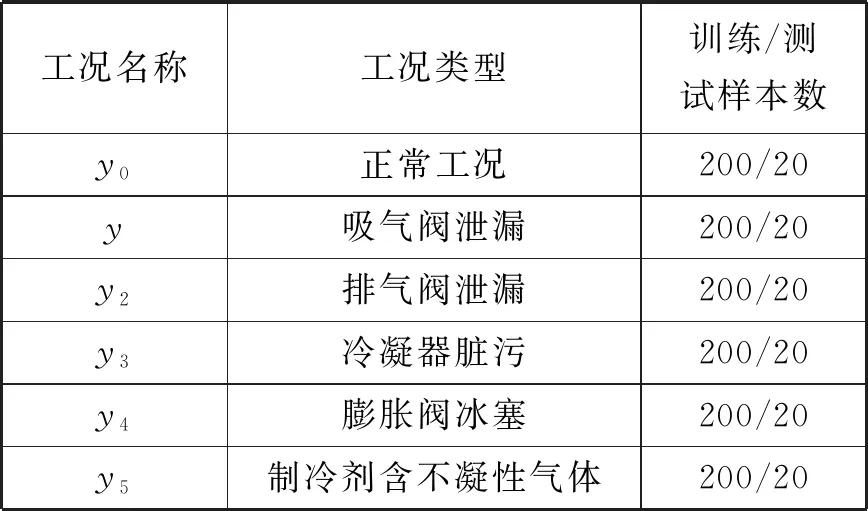
表1 工况类型和样本数
3.2 数据归一化
本文采用的归一化函数如下:
(24)
其中,xmax与xmin为样本数据的最大值和最小值;x为归一化前的数值;X*为归一化后的数值,其值在[0,1]之间。
3.3 故障诊断试验
经过试验发现y3故障与y5故障容易出现误诊并且诊断精度不高。因此,以y3故障为例应用本文方法进行诊断,证据体对y3故障诊断的基本概率分配值如表2所示。
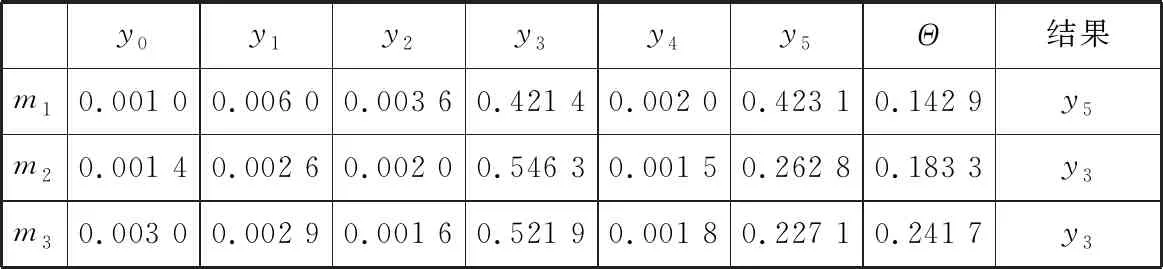
表2 y3故障诊断的基本概率分配值
根据公式(6)~(13),计算3个证据体的3个冲突衡量标准(差异性C1、冲突性C2、不确定性C3)定量数值,如表3所示。
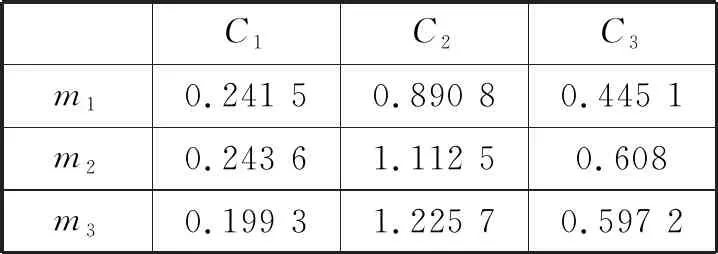
表3 各证据体的各冲突衡量标准数值
1) 准则层权重
根据表3计算各标准协方差矩阵,如表4所示:
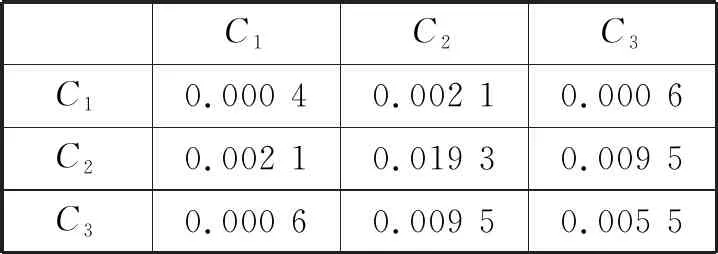
表4 各标准协方差矩阵
将表4中每个列元素除以对应列上的主对角元素得到各标准的相对协方差矩阵,如表5所示。

表5 各标准相对协方差矩阵
根据式(14)、(15)将表5进行变换可以唯一确定各标准两两比较矩阵,如表6所示。
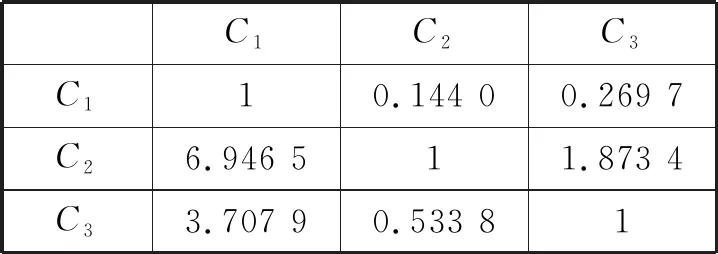
表6 各标准两两比较矩阵
采用平方根法计算,由两两比较矩阵得到各标准权重,如表7所示。
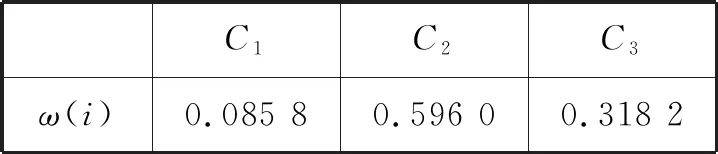
表7 各标准权重
2) 方案层权重
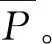
根据公式(19)~(20)可以得到各标准的优先级指标矩阵为:
根据公式(21)可以得出各标准下各方案权重,如表8所示。
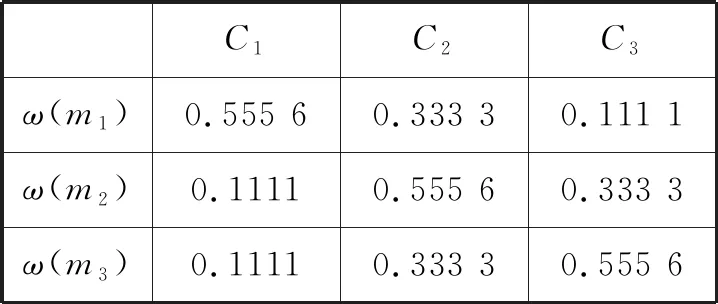
表8 各方案权重
3) 各证据权重
根据公式(22)将准则层和方案层进行组合,得到各个证据的权重,如表9所示。

表9 各证据体权重
由该表可以看出,证据体SVM(m1)的权重最小,这与前文中证据体SVM出现误诊的结果相符合,证据体GA-SVM(m2)的权重值最高,说明其提供的信息最可靠。
4) 加权证据
根据各证据体的权重及式(23)得到加权证据(保留4位小数)如下:
对加权证据进行两次融合,不同方法对y3故障诊断结果如图4所示:
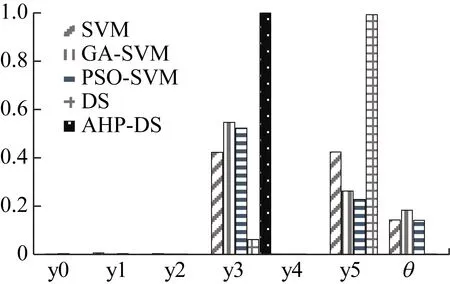
图4 不同诊断方法结果比较
从图中可以看出,传统DS融合时出现误诊,诊断结果高度支持y5故障,AHP-DS方法可以获得对y3故障最高的支持度,该方法可以在证据冲突较大的情况下保证诊断精度。
由表10可以看出,AHP-DS方法有效提升了y3和y5故障诊断正确率,并且未对其他故障的融合诊断产生不良影响。
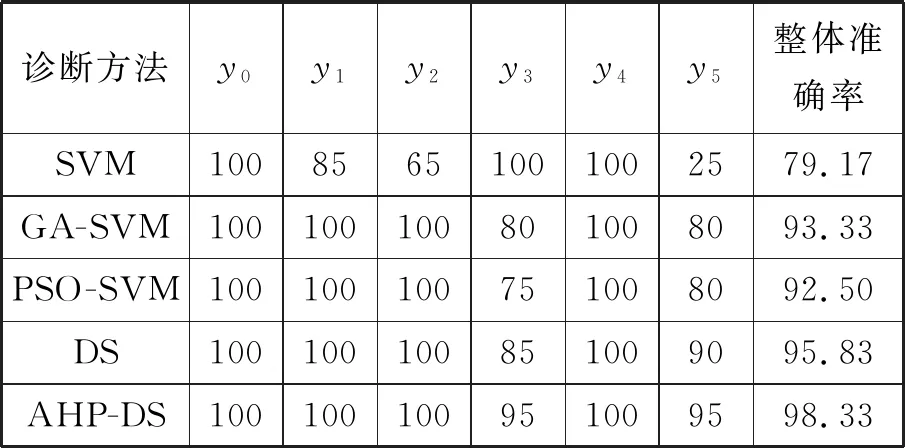
表10 测试集故障诊断准确率/%
4 结束语
本文的AHP-DS证据融合方法综合3个冲突衡量标准,通过船舶空调系统试验分析,证明其在处理高冲突证据融合表现良好。同时相比于单一SVM诊断模型,通过对3个证据体进行加权融合,提升了整体的故障诊断精度。但是改进后的算法在计算复杂度方面有所增加,所以其仍具有进一步优化提升的空间。

