基于AIS数据的船舶航迹多维预测方法

高大为， 朱永生， 张金奋， 鄢博冉， 何延康， 闫 柯

(1.西安交通大学 现代设计与转子轴承教育部重点实验室， 陕西 西安 710049；2.武汉理工大学 智能交通系统研究中心， 湖北 武汉 430063)

船舶实时航行轨迹的预测精度不高是造成船舶碰撞、船-桥碰撞等典型水上交通事故的重要原因之一。[1]船舶的轨迹可描述船舶状态，也可用于船舶的导航、避碰和海事监管，从而提升船舶航行安全性。随着近年来数据挖掘(Data Mining, DM)技术的兴起，越来越多的技术手段被用于船舶轨迹的挖掘与预测，试图基于历史船舶航迹数据来预测未来一段时间内的船舶航迹，从而感知潜在的航行风险，以便及早采取有效措施避免船舶的碰撞问题。

1)在轨迹预测问题上，DM技术已在多个领域得到了应用。ZHANG等[2]提出使用矩阵神经网络来预测气旋轨迹，避免对数据矢量化所造成的空间信息关联性的缺失，并通过试验证明其相对于循环神经网络具有更强的优势；HAO等[3]提出一种基于长短时记忆网络(Long Short-Term Memory,LSTM)的行人轨迹预测方法，不仅考虑社会邻域的影响，还考虑了场景布局对预测结果的影响；LI等[4]基于测距传感器和相机图像中所学习到的三维姿态数据，提出一种三自由度行人姿态轨迹预测方法;ALTCHÉ等[5]针对目前的先进驾驶辅助系统(Advanced Driving Assistance Systems, ADAS)无法进行中期预测的问题，提出一种预测未来公路上车辆横向和纵向轨迹的方法，从而将车辆所能预测到的轨迹延长。

2)在船舶的轨迹跟踪方面，相关技术也日渐成熟。基于船舶自动识别系统(Automatic Identification System, AIS)进行船舶轨迹预测的研究也越来越多。然而，由于AIS系统自身的问题、不适当的使用以及信号传输问题等原因，数据在时间和空间两个维度常存在较大的误差。针对该问题，ZHAO等[6]对数据集进行物理完整性、空间逻辑完整性和时间准确度等多重完整性维度的系统性分析，提出一种提高数据质量的算法;LIU等[7]使用张量分解工具提取了AIS数据中固有的运动模式，并基于链路预测技术来恢复全数据的张量，以解决船舶数据的缺失问题；徐铁等[8]提出使用kalman滤波算法来解决由AIS数据不可靠而导致的船舶轨迹不准确或者误差较大的问题;邓胡滨等[9]使用kalman滤波器来消除接收信号强度指示(Received Signal Strength Indicator, RSSI) 技术中环境因素的干扰。然而，基于预测算法的AIS数据需要保证具有等时间间隔的位置信息，而这些方法可提高数据质量，却难以直接进行预测。

3)在船舶的航迹预测问题上， SIMSIR等[10]基于船舶交通管理系统(Vessel Traffic Services, VTS)，使用船舶的位置和速度数据训练人工神经网络，依靠所预测的船舶航迹数据来解决狭窄水域的船舶预警问题;GAN等[11]基于大量的船舶轨迹数据，利用模糊C均值(Fuzzy C-Means, FCM)聚类算法对船舶历史轨迹进行聚类，建立船舶速度、载重、自重、最大功率、船长、船宽、船型和水位等已知因素的关系模型，解决了较长距离的船舶轨迹的预测问题，是一种典型的区域预测模型；权波等[12]提出使用基于LSTM模型对AIS数据进行建模和学习，实现船舶航行轨迹多维度特征表达，满足对船舶轨迹预测的精确度和实时性的需求；徐婷婷等[13]提出基于BP神经网络的船舶航迹预测方法，将航向和航速作为输入，经度、纬度差作为输出来建立航迹预测的模型实现实时的航迹预测。文献[12]和文献[13]属于典型的当前航迹预测模型。然而，这些方法一方面需以信噪比较低的AIS数据进行预测，当噪声较大时，难以实现理想的效果；另一方面，只使用当前航迹数据预测难以达到理想的预测精度。

针对以上问题，本文提出一种消噪和多维预测相结合的方法来预测船舶航迹。针对AIS数据中经、纬度值波动性大，有局部增大或减小趋势的特点，首先使用三次样条插值、中值滤波方法对经度、纬度差值进行消噪处理；然后对数据进行时间和空间两个维度上的建模，利用LSTM进行训练并综合两方面的信息，最后利用训练后的模型预测船舶的航迹信息。

1 LSTM的理论模型

LSTM作为一种捕捉序列化数据中动态信息的神经网络，通过记忆存储单元实现对序列数据的准确预测，已在机器翻译等领域有了较为成熟的应用。[14-15]LSTM在数据预测方面有强大的功能，相比于许多预测方法可获得更高的预测精度。其体系结构的核心思想是能够存储时变状态的存储单元，其非线性门单元可控制信息的流入和流出。LSTM通过遗忘门、输入门和输出门等3种结构实现信息保护和控制，其结构图见图1。图1中：将各个时刻的信息输入到不同的循环单元中，循环单元间可传递和输出信息，并由末尾的循环单元形成最后的输出。

图1 LSTM结构图

图1中遗忘门、输入门和输出门分别为

Ct=σ(Wf×[ht-1,xt]+bf)×Ct-1

(1)

Ct=Ct+σ(Wi×[ht-1,xt]+bi)×

tanh(WC×[ht-1,xt]+bC)

(2)

ht=σ(Wo×[ht-1,xt]+bo)×tanh(Ct)

(3)

式(1)～式(3)中：Ct为当前时刻t的状态胞体；ht为胞体的输出；xt为当前胞体的输入；Wf为各个门的权重；bf为所对应的偏差；σ为sigmod激活函数。

2 基于LSTM的船舶多维预测方法

多维预测方法包括AIS数据预处理、多维预测模型建立和预测。其中：AIS数据预处理是对数据进行消噪，使其更接近于真实值；多维预测模型则考虑了当前航迹数据和历史航迹数据，使预测结果更加准确。

2.1 AIS数据预处理

由于AIS数据在时间和空间两个维度存在较大的误差，甚至有时存在较明显的数据缺失问题，先对AIS数据进行预处理。受到AIS数据发送频率不一致等因素的影响，接收到的数据的时间间隔在大多数情况下是不统一的。因此，采用三次样条插值法来拟合数据。假设时间序列区间[a,b]可分成n个区间，即[(x0,x1),(x1,x2),…,(xn-1,xn)]，共有n+1个数据点且对应的函数值分别为y0,y1,…,yn。若插值函数S(x)满足

S(xi)=yi(i=1,2,…,n)

(4)

式(4)在各个小区间上都是不高于三次的多项式，假设为

Si(x)=aix3+bix2+cix+di

(5)

式(5)中：ai、bi、ci和di为待定系数。若三次样条方程满足曲线光滑的条件，即S(x)、S′(x)和S″(x)连续，则除了根据每个节点处的值建立方程组外，还可根据该连续条件建立方程组

S(xi-0)=S(xi+0)

(6)

S′(xi-0)=S′(xi+0)

(7)

S″(xi-0)=S″(xi+0)

(8)

在此基础上，再加上边界条件即可求得所有三次样条方程的系数，从而构造出整个插值函数。当计算某个点的插值时，则可由其所处的区间代入方程求得。

由于船舶的速度和航向经常发生变化，经纬度值具有较大的波动性，使用原始的AIS数据进行建模预测容易造成较大的误差。因此，在三次样条插值之后，进一步使用中值滤波的方法，分析该时刻邻域内的多个数据来计算在该时刻的信息。

在对原始AIS数据进行插值处理后，接着使用中值滤波来对其进行去噪。设AIS数据的第i个点为x(i)，由其周围2N个数据点组成的数据集合为

[x(i-N),…,x(i),…,x(i+N)]

(9)

则进行中值滤波后该点的值为

x′(i)=Med[x(i-N),…,x(i),…,x(i+N)]

(10)

式(10)中：Med为该数据集合的中间值。

中值滤波的优点在于对如AIS数据这种单位时间内的位移波动较大的数据，可起到较好的消噪效果。

2.2 多维预测模型

本文将船舶利用当前运动航迹进行预测时的模型称为“当前航迹模型(Current Trajectory Prediction Model, CTPM)”。CTPM已在多篇文献有所介绍。[12]该模型由船舶当前航行的数据建模，可反映船舶的实时状态信息、自然环境状态信息等。然而，该模型未能考虑船舶的空间位置特点。而船舶的航行状态与所在水域的空间位置具有较大的关联性。例如:在较窄的水域内，船舶的航行速度会较慢;在较宽的水域内，船舶的航行速度则会较快；在船舶接近港口时，速度会较慢；在弯曲航道，船舶一般会采取转向操作。因此，在CTPM的基础上，建立“区域预测模型(Regional Prediction Model, RPM)”。

RPM是指船舶利用预测时刻所处区域的位置信息建立模型，通过该区域的历史轨迹来分析所预测时刻的航行轨迹。RPM与CTPM是一种互补关系，通过将两者结合来提高对船舶航迹的预测能力。CTPM提取当前船舶的航行状态特征；RPM提取空间位置的水域特点对船舶航行状态所影响的特征。

由于在短时间内，相邻AIS数据间的经纬度差值一般较小(10-5到10-4甚至更小的范围内)，而该数值的量级会给模型的训练带来较多的困难。因此，选用经纬度差值来作为预测模型在单个时刻的输入和输出，同时，将航速、航向信息作为模型的考虑因素，见图2。图2中：对于CTPM来说，使用相邻数据点的差值作为输入；而对于RPM而言，则将其中一个航迹设为参考数据，利用与其差值作为输入。

图2 LSTM模型在t时刻的输入与输出

对RPM来说，设{Xi,j|i∈m,j∈n} 为船舶的某区域历史航迹，其共有m段航迹，n个位置。

Xi,j=[xi,j,yi,j,vi,j,dij]

(11)

式(11)中：xi,j、yi,j、vi,j和dij分别为船舶在某个位置的经度、纬度、速度和航向。为避免网络训练中的数值问题，并使网络快速收敛，先对各个航迹数据进行归一化操作为

(12)

(13)

i∈{1,2,…,m})

(14)

同时，以当前航迹数据来训练CTPM为

(15)

式(15)中：

(16)

再用全连接层将二者融合来进行训练，最终的预测结果为

(17)

使用均方误差(Mean Squared Error, MSE)作为损失函数训练模型为

(18)

模型使用自适应矩估计优化器(Adam)对其进行优化。Adam是一种对随机目标函数执行一阶梯度优化的算法。模型隐藏层中的单元数通过在{85, 170, 255, 340, 425} 中搜寻最优的值来作为此处的参数，用于记忆和存储过去的状态。最大训练周期数的选取需要保证模型可以收敛，在此根据模型多次试验结果选择为1 500，循环层个数设置为3，预测步数设置为1。使用训练好的模型预测数据后，再将数据还原成经纬度值。船舶航迹预测模型见图3。

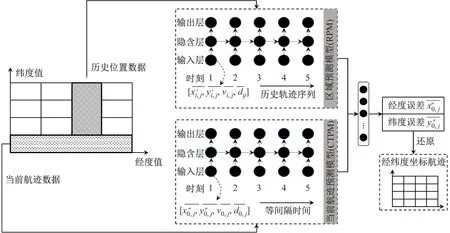
图3 船舶航迹预测模型

2.3 船舶航迹预测流程

对于船舶的航迹预测来说，一方面，前一时刻的经纬度差值位置信息决定着待预测时刻的经纬度值位置信息；另一方面，船舶的航速、航向也对经纬度差值存在着较大的影响。因此，以经纬度差值、航速、航向等4个参数作为网络的输入，以经、纬度差值作为输出。方法流程见图4。

图4 所提出方法流程

1)对原始数据进行预处理，对其进行初步判定、插值处理等，从而获得等时间间隔的经纬度、航向和速度信息。

2)选取指定间隔的相邻数据点的经纬度差值。

3)通过中值滤波方法进行滤波。

4)基于船舶空间历史数据，构造区域范围内的船舶轨迹预测模型RPM。

5)基于船舶的实时数据，构造船舶当前航迹预测模型CTPM。

6)联合对以上模型进行训练。

7)获得实时预测的经纬度差值。

8)将其还原成经纬度值。

3 试验数据分析

为测试提出的轨迹预测算法的性能，分别使用海上AIS数据和内河AIS数据来训练模型并预测。

3.1 案例1：海上航迹预测

海上AIS数据为大连、烟台2个港口之间的数据，该水域的经纬度值见图5。由图5可知：在相同任务的航行中每艘船舶的航行轨迹在大体趋势上存在较大的相关性，但在各个位置处仍然存在着一定的差别。本文选取其中一段数据来验证所提出方法的效果。

图5 某个范围内的船舶经纬度值

首先对AIS数据进行预处理，根据初步判断法则去除明显的异常数据。然后使用三次样条插值，使其在时间上等间隔。对预处理后的经纬度数据进行差值处理，即获得等间隔时间段内船舶的航行里程信息，然后对经纬度差值进行消噪处理，结果见图6。由图6可知：消噪前的经纬度差值数据(图6中灰色部分)存在以下特点：在经纬度差值较为稳定的阶段，其以某个数据值为中心，存在“正弦式”波动的规律；在某些阶段其经纬度差会出现局部的增大或减小。对于前者，对该数据的消噪可使用均值滤波法，然而考虑到后者中出现的局部增大或减小，使用中值滤波可同时满足以上两方面消噪的需求。消噪后的数据如图6中黑色曲线所示，经中值滤波消噪后数据的波动性得到较好的解决，且能保留局部出现的增大或减小的趋势。

a) 经度差

选取经纬度从(121.504 9°E, 37.771 0°N)到(121.585 3°E, 37.983 1°N)的一段数据进行分析，通过寻优设置隐含层数为170，预测结果见图7。

a) 整体预测结果

图7中：实际值为实际的航行轨迹；训练值为训练网络所使用的的经纬度差值部分；测试值为进行预测的部分。由图7可知：船舶的航行轨迹预测精度较高，与实际值的趋势一致。图7b结果为在图7a的基础上进行局部放大的某段训练数据，图7c和图7d为测试数据上船舶某两段轻微转弯时的轨迹，预测结果可看出，虽然测试值与实际值出现了一定的偏差，但是误差较小，预测效果良好。

预测误差可更为直观的反映模型的性能，预测得到的经纬度误差见图8。再结合该案例中的时刻差(6 s)可知:二者的均值分别为6.23×10-5°和8.89×10-5°。同时，本文将该方法与传统的LSTM方法进行对比见表1。由表1可知：在经度、纬度两个方向上，所提出的方法均能获得较小的误差，证实所提出方法的有效性。

a) 经度误差

表1 两种预测方法的平均误差的对比

3.2 案例2：内河航迹预测

为进一步测试提出的轨迹预测算法的性能，使用某段内河的AIS数据进行分析。所研究水域的经纬度数据见图9。由图9可知：在相同任务的航行中各个船舶的航行轨迹在大体趋势上存在较大的相关性，但在各个位置仍存在着一定的差别。本文选取船舶直线行驶、船舶转弯、船舶加速和船舶减速时的AIS数据等4段典型数据，来验证所提出方法的效果。该4段数据以不同的标记展示在图9中。

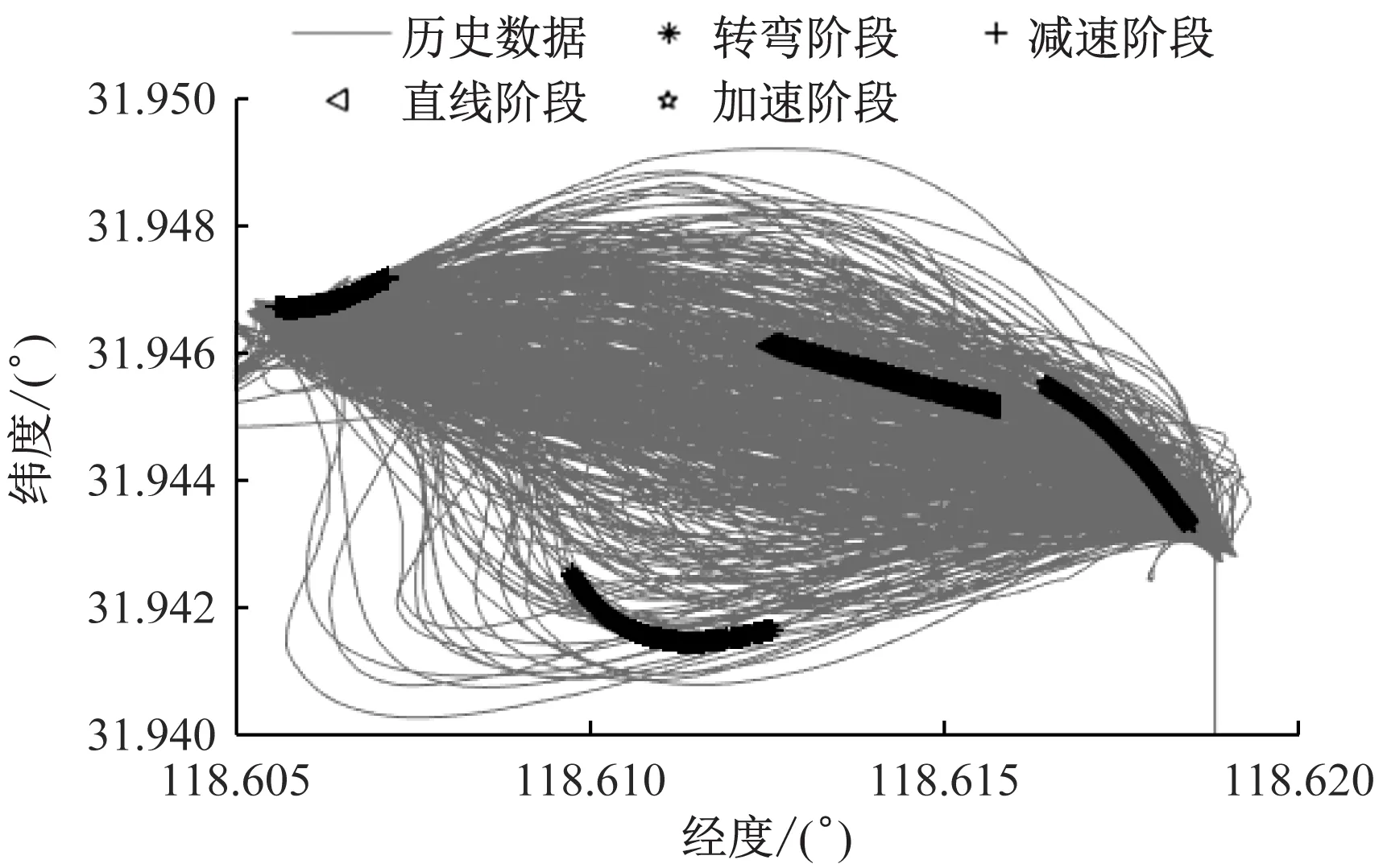
图9 某个范围内的船舶经纬度值

在进行模型预测之前，首先使用上述数据预处理方法对航迹数据进行三次样条插值和中值滤波，随后再进行航迹预测。通过寻优设置隐含层数为170，预测结果见图10～图13。由图10～图13可知：该预测方法在船舶的各个阶段都实现了较为准确的预测。

在直线行驶阶段如图12所示，船船航迹的预测误差最小，其最大预测误差低至7.0×10-7°。在图13所示的转弯阶段，船舶的预测误差相对较大些，这是由于训练数据中没有学习到船舶转弯时的状态信息。同时，在船舶加减速阶段如图10和图11所示，其预测误差相比直线阶段也要略大一些。然而，相比于所预测时间内的船舶位移，该误差在可接受的范围之内。为验证方法的有效性，同时，将该方法与传统的LSTM方法进行对比，结果见表2。由表2可知：虽然直线阶段二者差别不大，但是在其他的航行状态下，所提出的方法的预测误差明显较小。通过以上分析，说明所提出的预测模型在内河AIS数据中也可达到较好的效果。

a) 预测结果

a) 预测结果

a) 预测结果

a) 预测结果

表2 两种预测方法的平均均方根误差的对比

4 结束语

本文提出一种基于船舶AIS数据的航迹多维预测方法，首先通过3次样条插值、中值滤波等技术对数据进行预处理，然后在此基础上基于历史轨迹数据和当前航迹数据构建多维预测算法来提高预测的精度。在数据预处理环节，通过多种方法保证数据的可靠性；在航迹多维预测环节，分别建立区域预测模型和当前航迹预测模型，从时间和空间两个维度同时对航迹进行预测并综合其结果。通过海上AIS数据和内河AIS数据的试验验证，结果表明所提出的方法可实现对船舶航迹较为准确的预测。