基于分轴燃气轮机发电的混合动力系统建模与分析

李鸿扬， 温旭辉， 王又珑

(1. 中国科学院电力电子与电气驱动重点实验室，中国科学院电工研究所， 北京 100190;2. 中国科学院大学， 北京 100049)

1 引言

用于下一代全电船舶或飞行器的新型混合电力系统提供了将推进系统和机载服务电力系统相结合的通用电气平台，其结构如图1所示，通常包括以下模块：发电模块(燃气轮机-发电机及PWM整流器)，储能模块(锂电池)，电推进模块和其他负载。

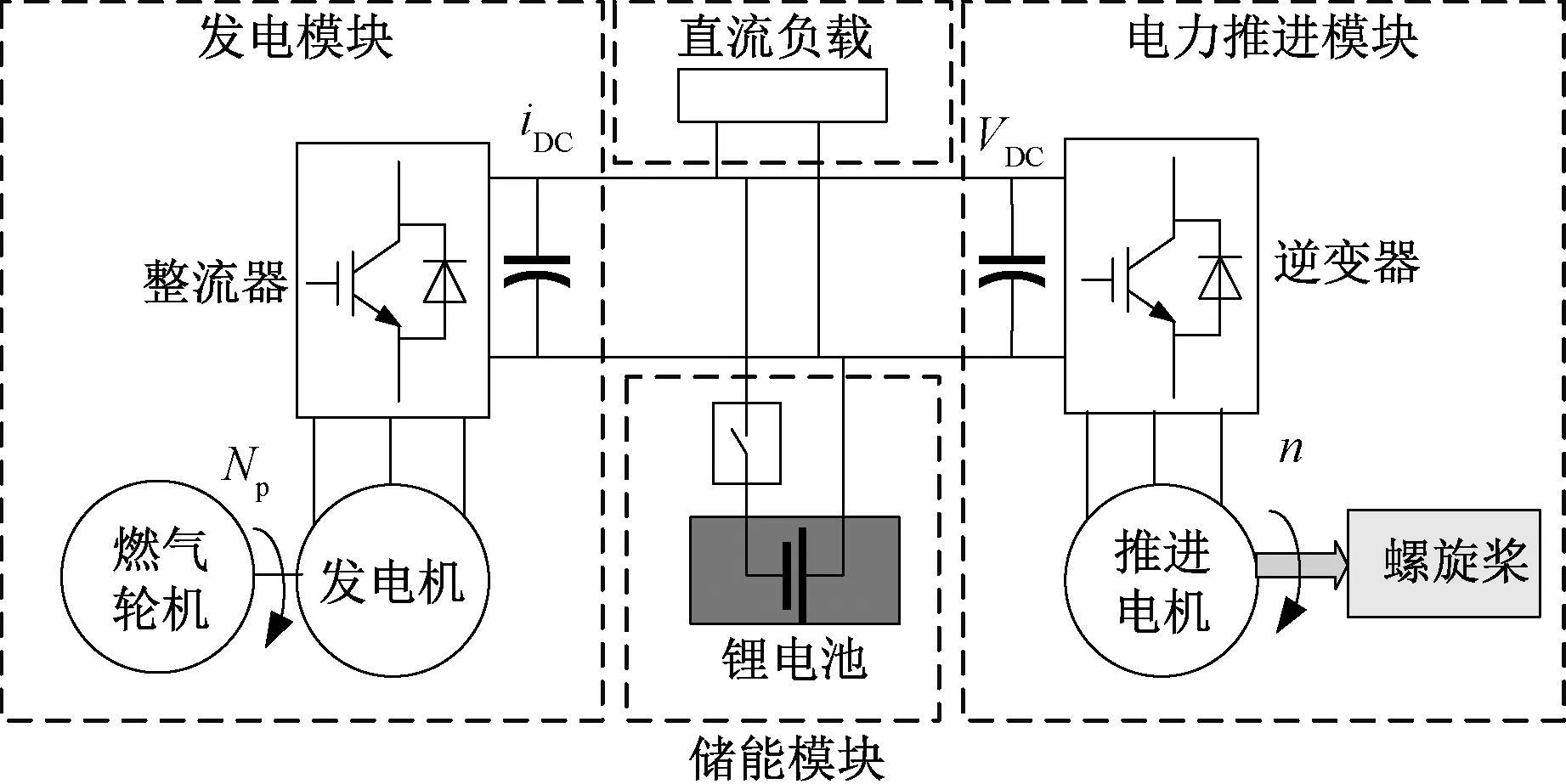
图1 系统结构图

传统燃气轮机发电系统多用于分布式发电或舰载电力系统，采用交流并网或不控整流斩波升压直流并网结构，具有负载变化慢、燃气轮机转速波动小等特点[1-5]。本文所研究的基于分轴微型燃气轮机发电的混合动力系统中，燃气轮机作为系统主要功率源，PWM整流器工作在恒压控制模式，为直流母线提供恒定电压。燃气轮机发电系统需要适应电推进模块大范围的功率变化，其转速波动范围更宽。需要建模分析动态过程和燃气轮机发电的暂态特性。

目前国内外燃气轮机线性化模型的研究集中在单轴燃气轮机上，此类燃机的旋转质量连接在高压涡轮上，如Rowen模型、IEEE模型及GAST模型等[4,5]。与此类燃气轮机相比，分轴燃气轮机的压缩机与动力涡轮连接在不同的轴上，能够以与动力涡轮不同的速度旋转，从而实现更优的压缩机特性，获得更好的整体性能，经常用于在部分负荷运行时以获得更好的经济性[4]。

文献[2]研究了微型分轴燃气轮机的建模控制方法，分析了微型燃气轮机的热力学特性，但该方法不能描述分轴燃气轮机发电系统的机械特性及电气特性。也有学者研究了微型燃气轮机发电系统建模，其中对燃气轮机模型的研究集中于单轴燃气轮机，且要求发电频率，即燃气轮机输出转速稳定，不适用于分轴燃气轮机输出功率及转速变化较大时的场合，且文献中的发电系统多为不控整流发电系统，直流侧多建模为简单的电压源或功率源，无法体现PWM整流器的开关特性及故障时的变拓扑特性[3,4]。

另一方面，一般来讲电力电子装置开关过程的暂态时间尺度是百微秒级，燃气轮机机械系统的暂态时间尺度是秒级，动力电池组的时间尺度为10～0.1 s，如图2所示[1]。传统的分析模型无法兼顾仿真精度与仿真时间的需求，其中考虑电磁过程的仿真模型，在普通计算机上能顺利运行的仿真时间一般不超过20 s，无法在该模型上进行机械系统动态过程仿真，更无法在仿真中体现机械与电气过程的相互影响。为此，混合动力系统正常运行、故障及故障后重新配置的工况通常都是独立进行仿真[6]，难以体现出发电机整流器故障对燃气轮机的动态影响。

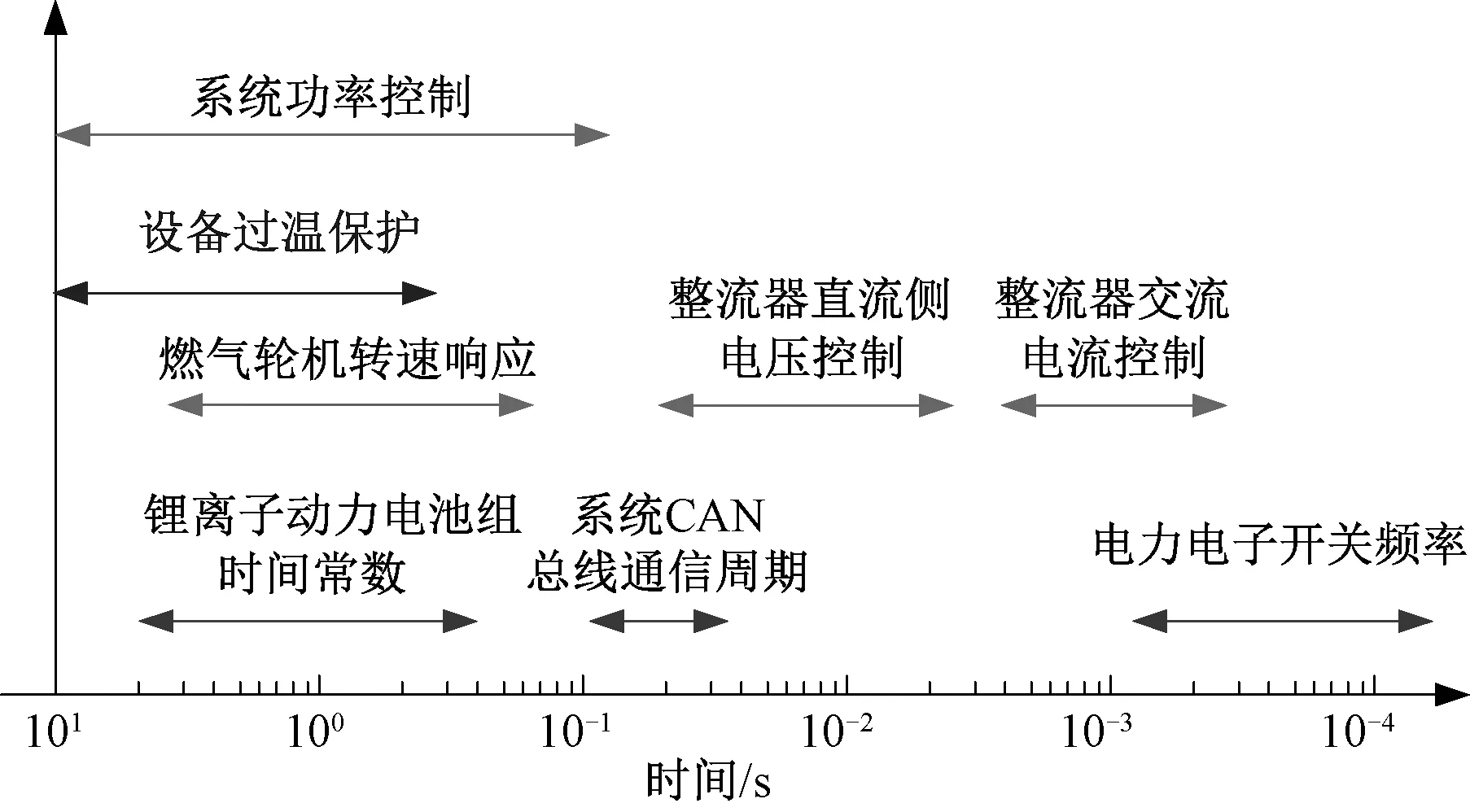
图2 系统带宽

为更好地兼顾仿真精度与仿真时间的需求，体现电气过程和机械过程的相互影响，本文改进了已有的微型燃气轮机的线性化模型，提出一种适用于故障及扰动分析的分轴微型燃气轮机发电系统模型及发电机整流器开关流图模型。所提出的模型可以在考虑电力电子装置微观动态过程的前提下实现对完整的机械系统时间尺度过程的仿真，可兼顾整流器正常运行、故障中和故障重构后对燃气轮机发电系统的仿真分析。

2 系统建模

2.1 分轴燃气轮机模型

为建立适用于频率宽范围变化的发电系统的分轴燃气轮机数学模型，假设：

(1)压气机入口温度与大气温度相等。

(2)压气机、燃气涡轮工质视为理想气体。

(3)以压缩过程的等熵效率来考虑压缩过程中的损失。

(4)以膨胀过程的等熵效率来考虑膨胀过程中的损失。

分轴燃气轮机结构如图3所示，由压气机、燃烧室、高压涡轮(High Pressure Turbine, HPT)、动力涡轮(Low Pressure Turbine, LPT)、回热器以及换热器组成[7-10]。TCom为压气机转矩，THP为高压涡轮转矩，TLP为动力涡轮转矩，B为燃料输入流量，Ng为高压涡轮转速，NP为动力涡轮转速。

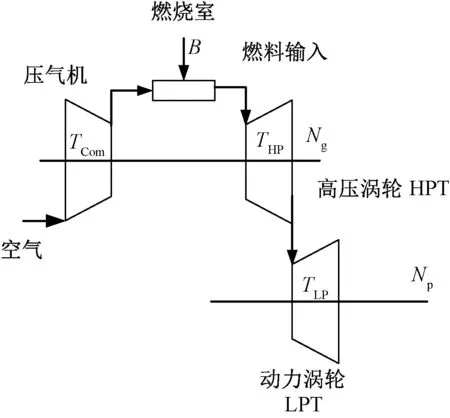
图3 分轴燃气轮机结构

常用的分轴燃气轮机的线性化模型为Aero-Derivative 模型[11]，与前面提到的Rowen模型、IEEE模型一样，仅在燃气轮机转速为95%～107%额定转速[12, 13]时较准确。 然而，本文研究的混合动力系统负载扰动大，且故障时功率波动大，导致燃气轮机转速波动范围较宽，普通线性化模型无法满足系统仿真需求。为了能够分析发电频率异常变化的工况，必须考虑燃气轮机模型的频率依赖性。

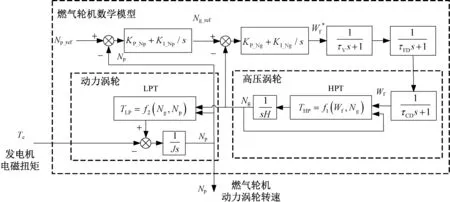
图4 简化双轴燃气轮机控制回路

Luca Bozzi提供了适用于发电厂和分布式发电应用的双轴燃气轮机的简化动态数学模型，其频率依赖性低，在高压涡轮50%～110%额定转速及动力涡轮15%～110%额定转速的工况有较高的仿真精度[14]。本文以此模型为基础，改进了其控制结构，简化了对转速控制影响较小的温度控制模块，提出了适用于分轴燃气轮机发电系统仿真分析的模型，如图4所示，其中，Wf为燃油流量指令，τV为燃油阀门时间常数，τFD为燃烧室时间常数，τCD为高压涡轮时间常数，THP为高压涡轮转矩，TLP为动力涡轮转矩，H为高压涡轮转子的转动惯量，J为动力涡轮转子的转动惯量。

2.1.1 转速调节器

对分轴燃气轮机，采用双PI控制器控制高压涡轮及动力涡轮转速，其中转速外环为动力涡轮转速控制，输出为高压涡轮转速指令Ng_ref。

Ng_ref=(NP_ref-NP)(KP_Np+KI_Np/s)

(1)

式中，Ng_ref为高压涡轮转速指令；Np_ref为动力涡轮转速指令；KP_Np和KI_Np分别为动力涡轮转速PI控制器的比例积分值。

内环为高压涡轮转速(HPT)控制，输出为燃油流量，燃油流量给定值Wf*(s)由高压涡轮控制器给出：

Wf*(s)=(KP_Ng+KI_Ng/s)(Ng_ref-Ng)

(2)

式中，Ng为高压涡轮转速；Ng_ref为高压涡轮转速指令；KP_Ng和KI_Ng分别为高压涡轮转速PI控制器的比例积分值。

2.1.2 燃料系统

与阀门定位器类似，式(3) 和式(4)的大信号模型分别代表阀门位置调节特性及燃料系统响应特性。

(3)

(4)

式中，Es(s)为燃料量的标幺值；Fs(s)为燃油流量的标幺值。

燃气轮机动态特性：燃气轮机动态特性可以等效成一阶传递函数，燃气流量的标幺值Wf(s)为：

(5)

根据文献[14]可计算燃料为燃油的燃气轮机，其燃料系统及燃气轮机高压涡轮特性时间常数。根据不同工况、不同频率下的实测数据对某型分轴微型燃气轮机的关键参数进行抽取，如表1所示。

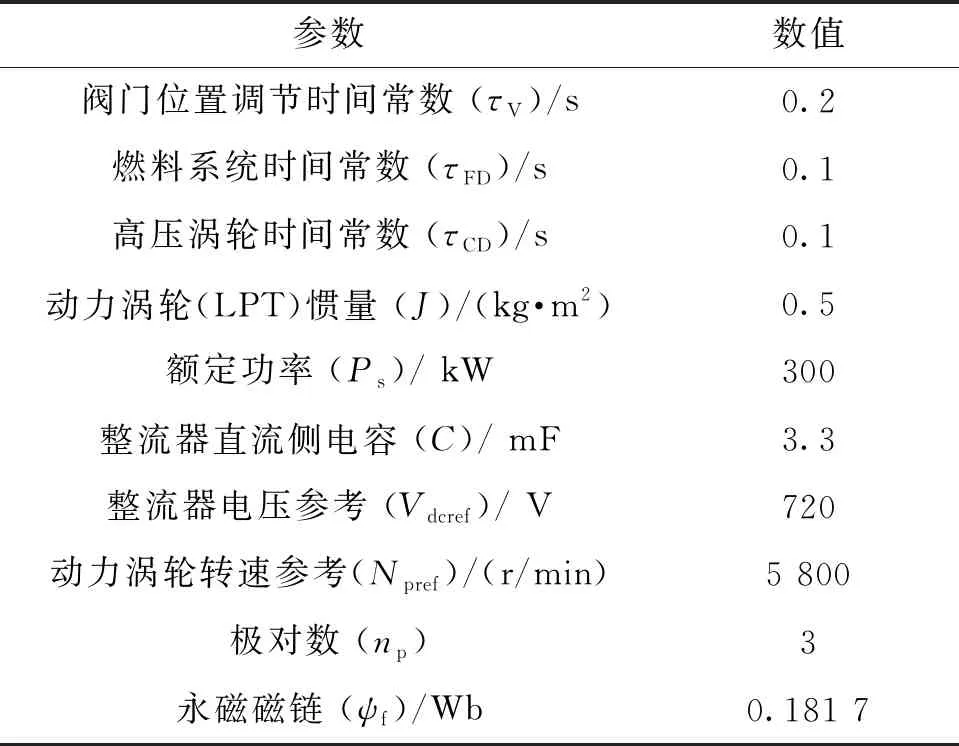
表1 系统参数

2.1.3 高压涡轮及动力涡轮

燃气轮机的高压涡轮(HPT)转矩方程和机械方程分别如式(6)和式(7)所示；动力涡轮(LPT) 转矩方程和机械方程分别如式(8)和式(9)所示。

THP=f1(Wf,Ng)

(6)

(7)

TLP=f2(Ng,Np)

(8)

(9)

式中，Te为发电机电磁转矩；ωNp和ωNg分别为LPT和HPT角速度。

燃气涡轮及动力涡轮的转矩方程可由燃气轮机运行数据进行拟合得到，拟合曲线如图 5和图 6所示，单位为标幺值。

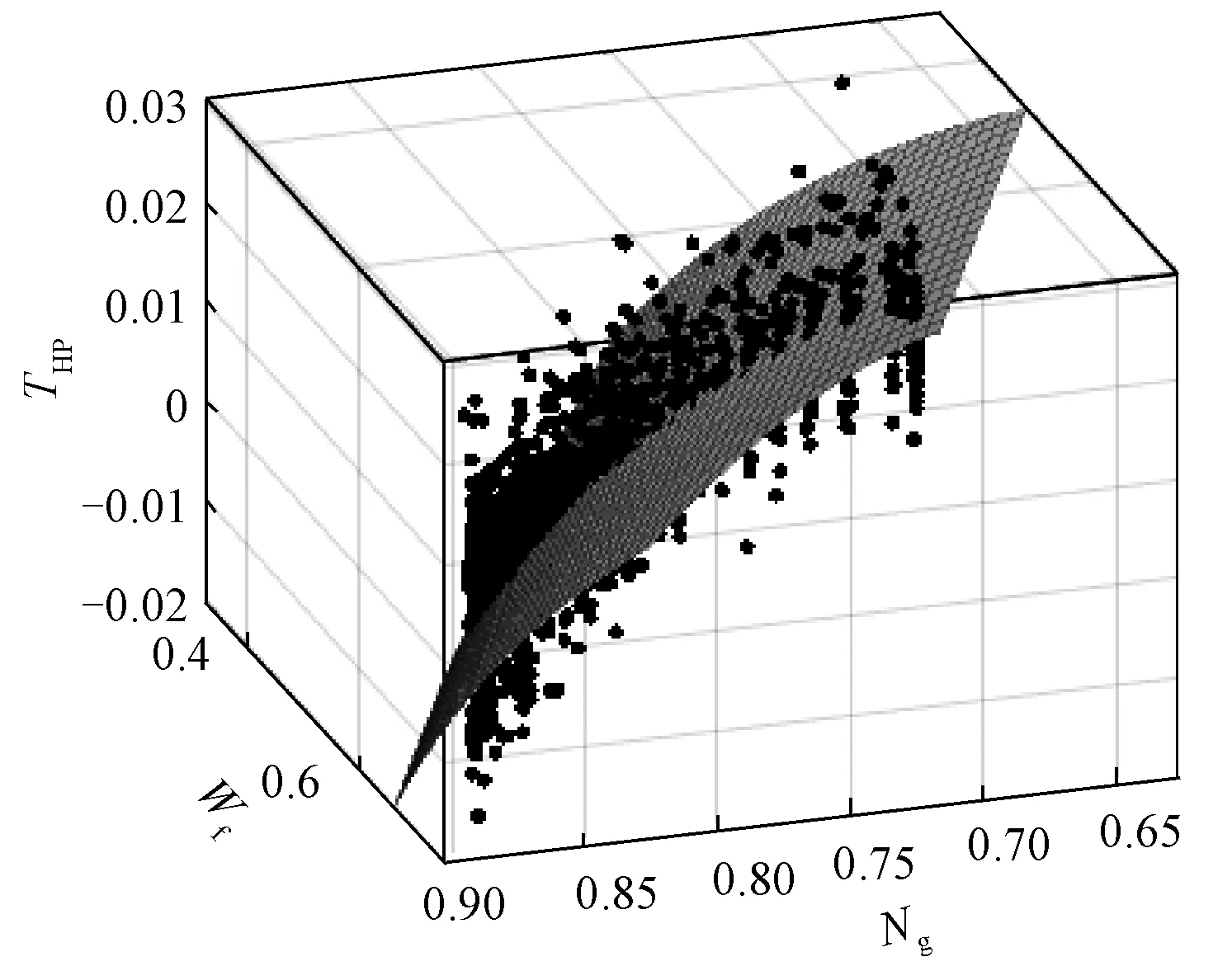
图5 高压涡轮转矩曲线拟合结果

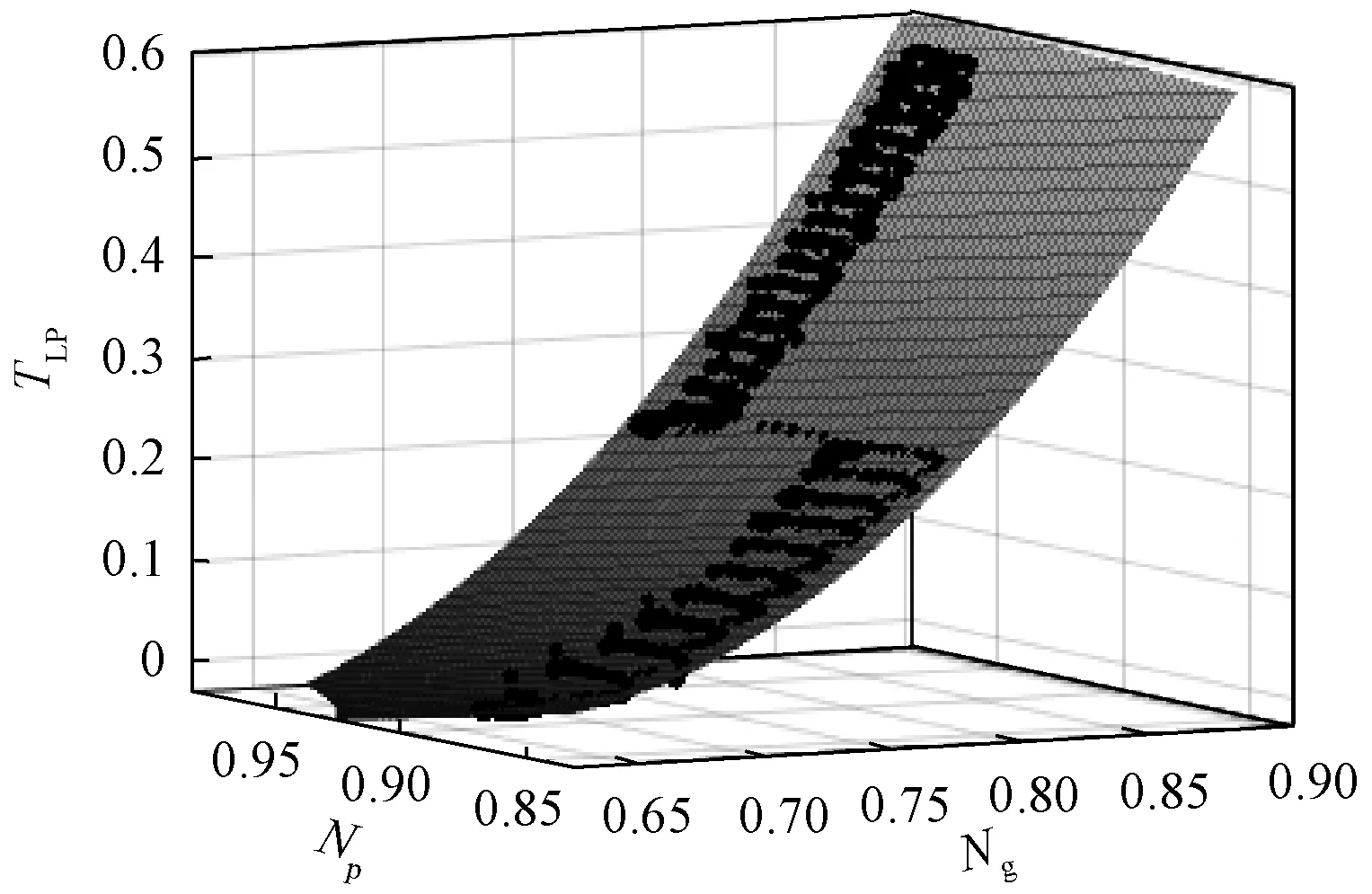
图6 动力涡轮转矩曲线拟合结果

高压涡轮及动力涡轮的扭矩方程由式(10)和式(11)给出。

f1=-0.3792+0.2057Wf+1.064Ng-0.9045Ng2

(10)

f2=1572-0.7142Ng+9.6828×10-5Ng2-0.478Np

(11)

2.2 永磁同步发电机及整流器模型

在建立数学模型之前，先做如下假设[14-16]：

(1) 忽略开关器件的导通压降和开关损耗。

(2) 忽略变流器分布参数的影响。

(3) 任何时候同一桥臂的上下管不应同时接通，以避免直流源短路。

三相PWM整流器及永磁同步电机模型如图7所示。图7中，ea,eb,ec为永磁同步电机三相气隙合成电动势(空载反电动势、定子dq轴电枢感应电动势及漏抗上的压降之和)；ia,ib,ic为电机三相相电流；SjP、SjN为同一桥臂上下管可控开关，DjP、DjN为反并联二极管；Sa,Sb,Sc为开关管的开关信号；Vdc为直流母线电压；R为定子电阻；C为直流侧电容；图7中，O、N点分别为电机三相绕组中点和变流器下桥臂共射极连接点。

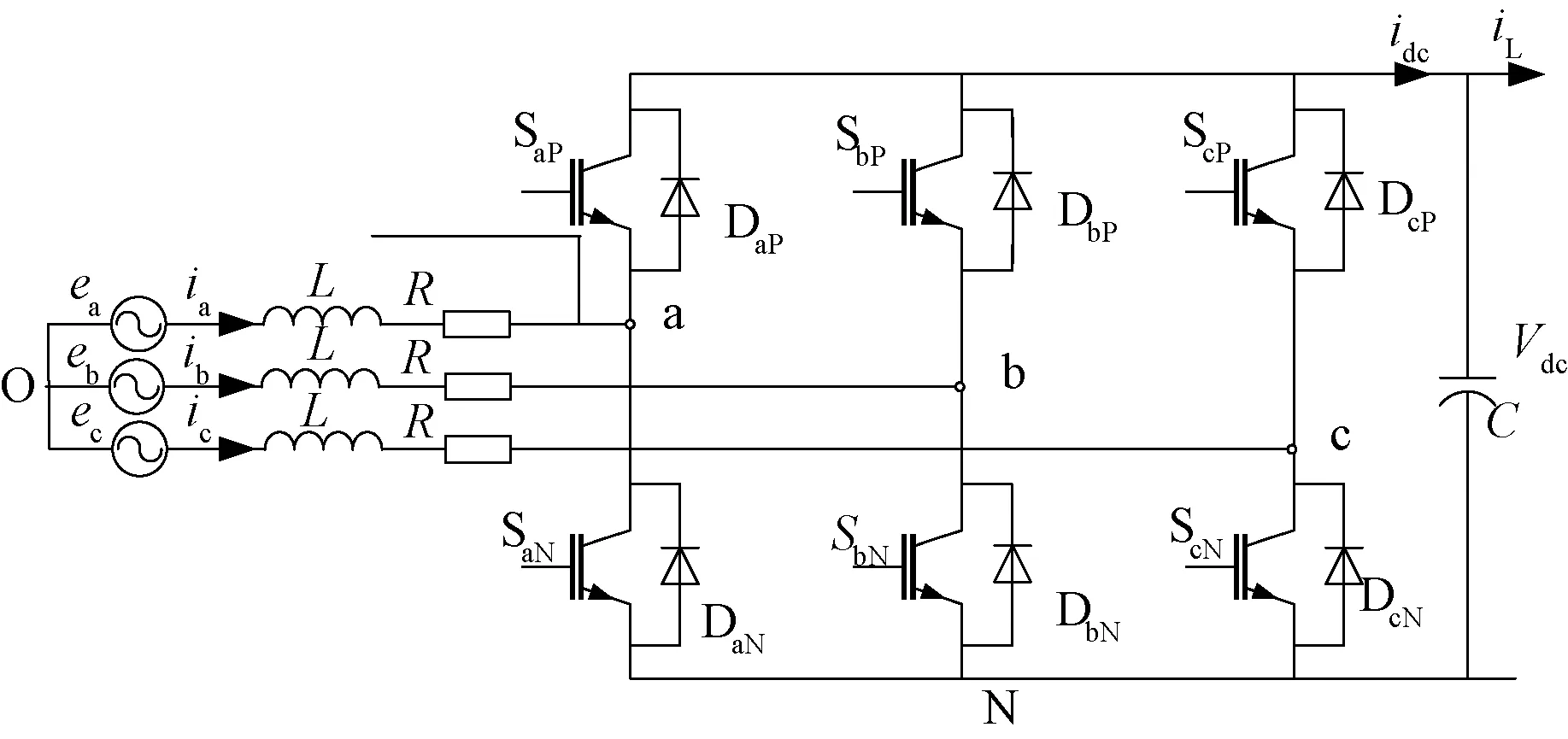
图7 三相PWM整流器及永磁同步电机模型

图7所示的可控开关Sjk，j∈{a,b,c}的开关状态{ON,OFF}可由以下开关函数定义：

(12)

式中，j∈{a,b,c},k∈{P,N}。

尽管DjP、DjN是不可控的，但是为了获得可以处理不同电压极性的简单切换流程图，式(13)定义了相应的开关函数，用于描述DjP、DjN的导通和关断状态。

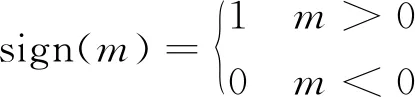
(13)

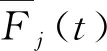
(16)

式中，⊗表示与运算；⊕表示或运算。PWM整流器及永磁同步电机的开关流图模型(Switching Flow-Graph, SFG)如图8所示。

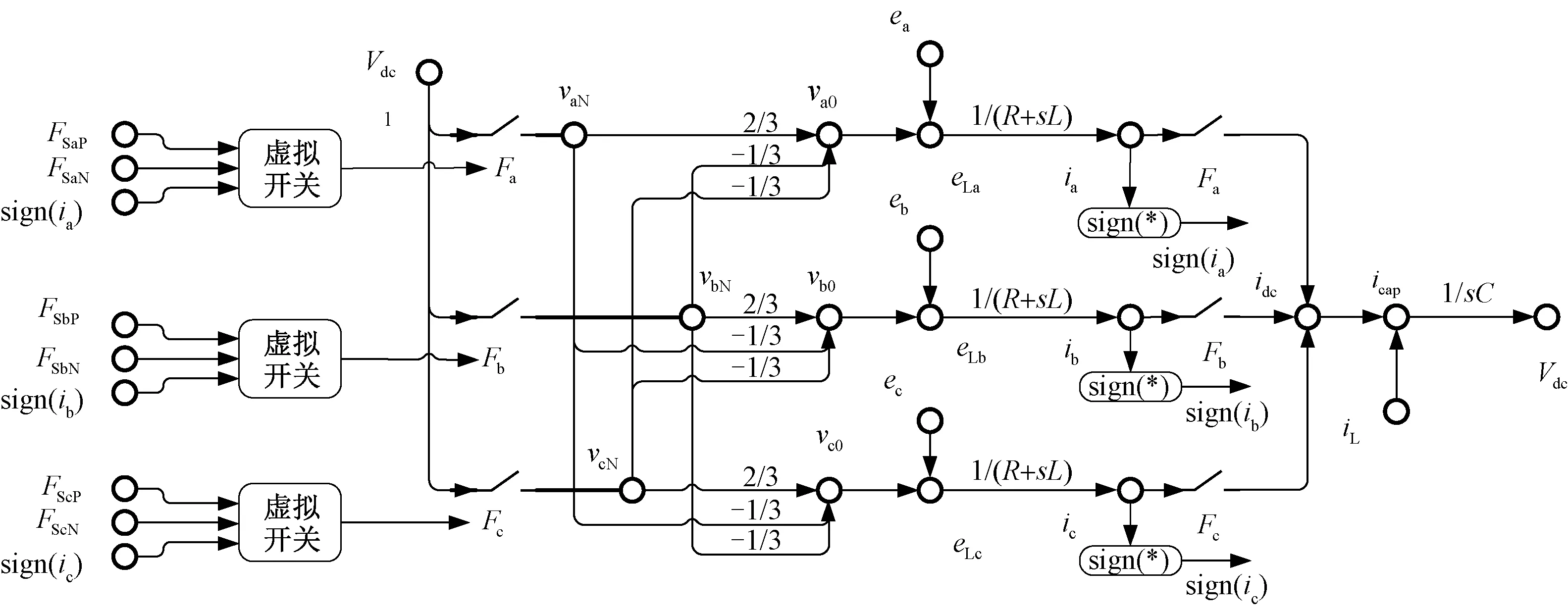
图8 永磁同步电动机及三相PWM整流器的开关流图

3 仿真及实验对比

3.1 燃气轮机模型仿真验证

将实验中燃气轮机转速指令及燃气轮机负载扭矩作为模型输入信号，在如图 9所示的Simulink仿真模型中进行仿真，得到的高压涡轮、动力涡轮转速响应Ng、Np与实验数据进行对比，结果如图 10及图 11所示。由仿真结果可以看出，动力涡轮转速Np在不同系统运行频率段，误差小于2%，满足故障及大负载扰动等仿真需求。

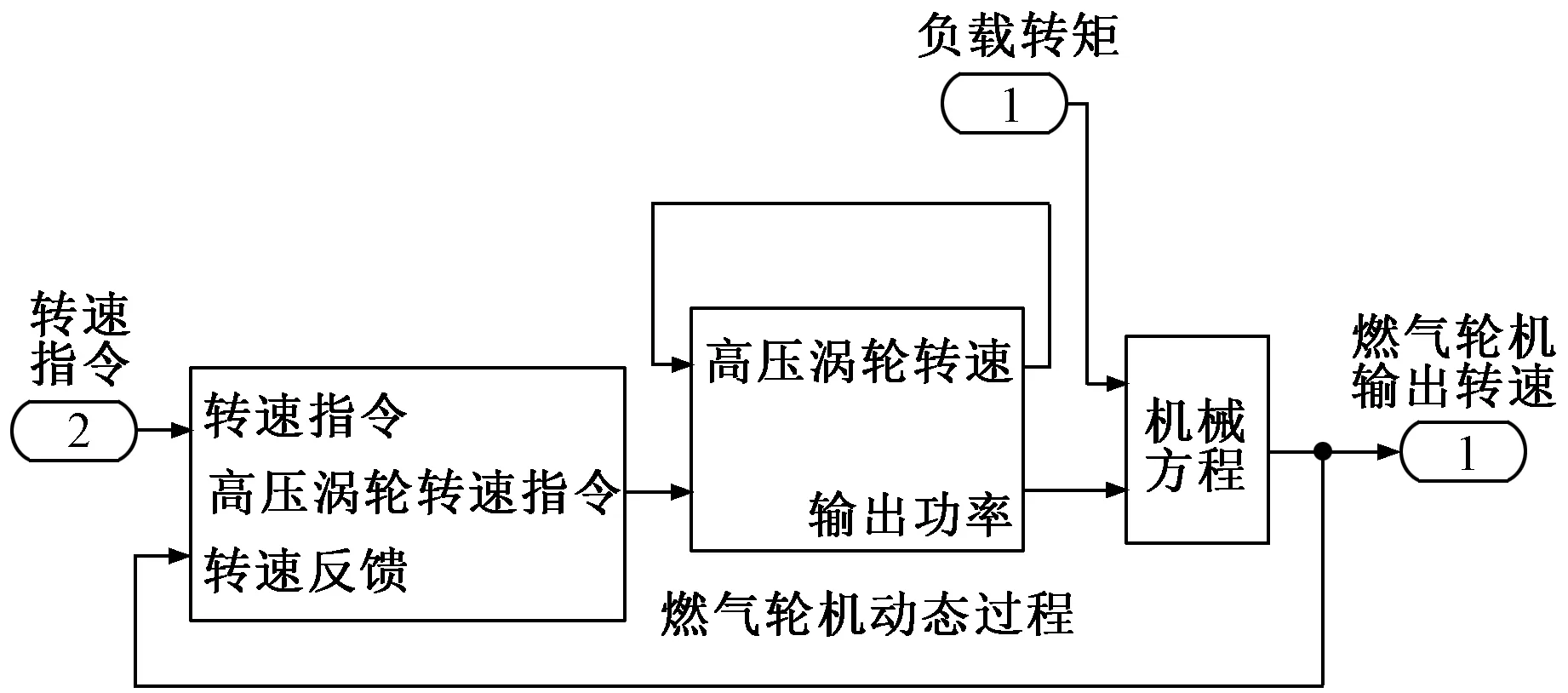
图9 燃气轮机的Simulink模型

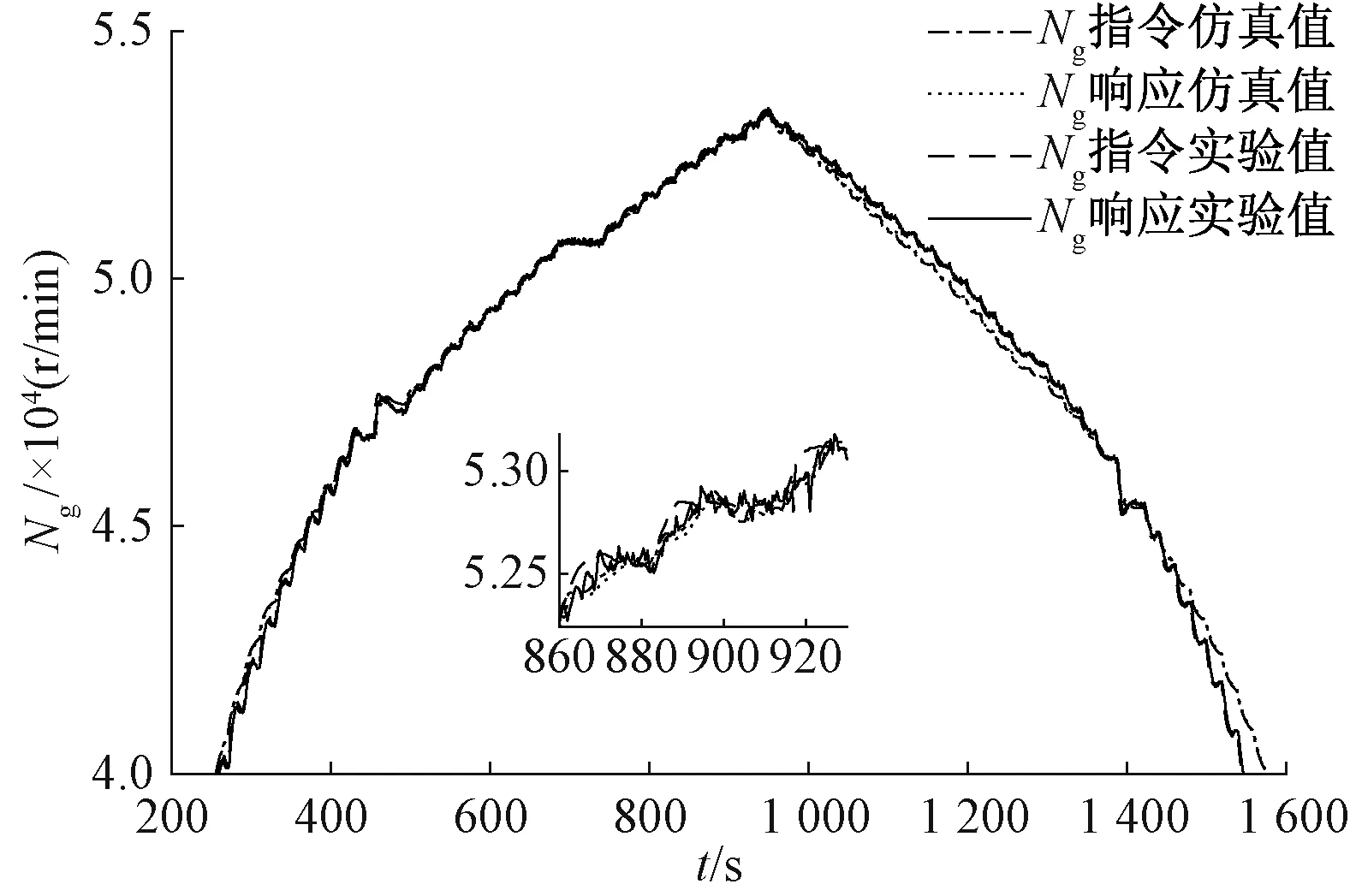
图10 燃气涡轮Ng转速响应，仿真与实验结果对比

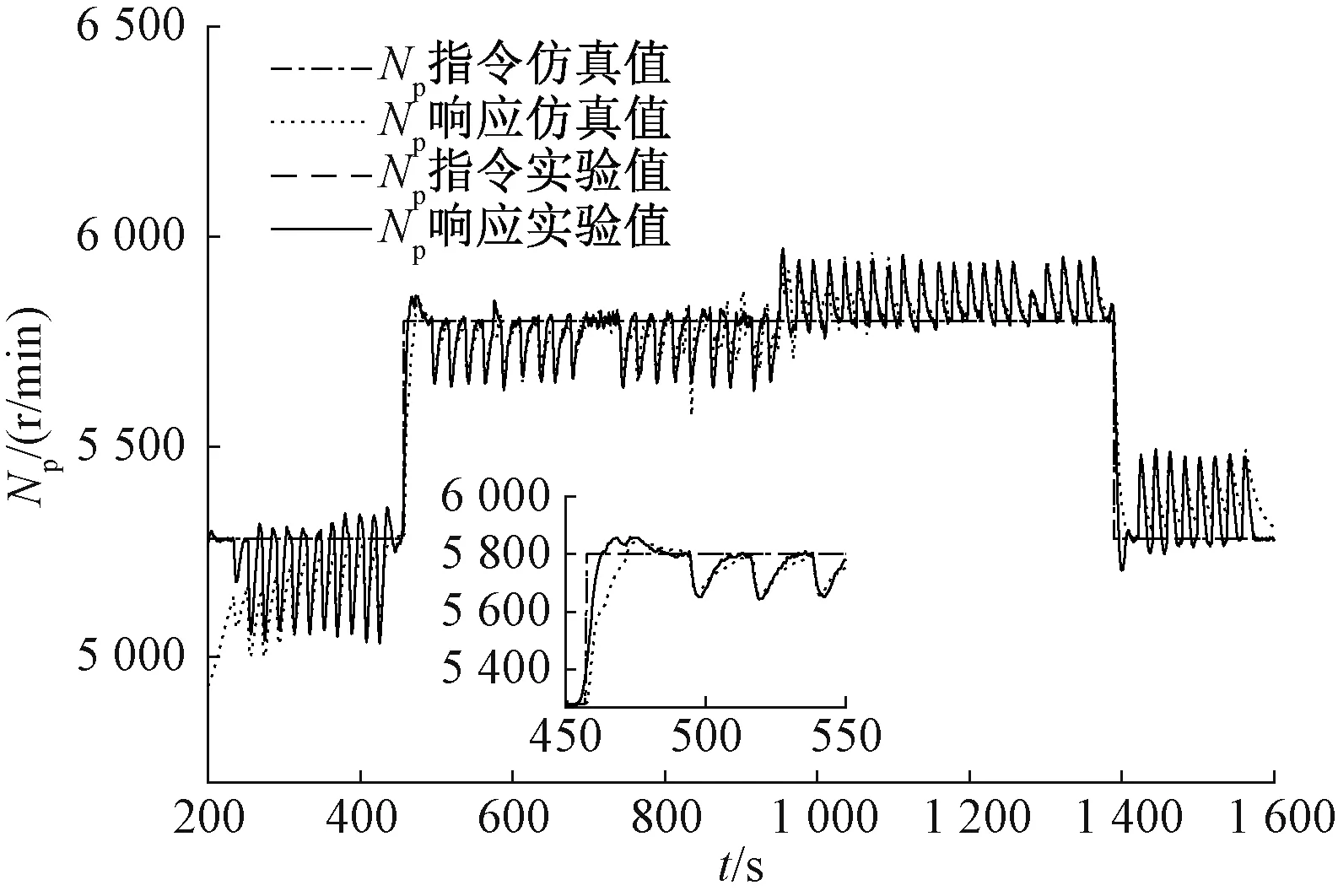
图11 动力涡轮Np转速响应，仿真与实验结果对比

3.2 发电机整流器仿真验证

在Matlab/Simulink中按照实际系统拓扑搭建系统模型，如图12所示，与Simulink/Simpower system模型的仿真结果进行对比。

在MATLAB / Simulink下用相同的初始条件对Simpowersystem搭建的模型与基于SFG的发电机整流器模型进行仿真，将死区时间分别设为0和20 μs，得到对应的a相电流ia和直流电压Udc，分别如图 13和图14所示。两个模型结果高度吻合。但是，使用开关流图模型比使用Simulink /Simpowersystem占用计算资源少，计算时间短。例如，对于1 μs的仿真步长和10 s的仿真时间，Intel Core i7-8750H @2.2GHz的计算机使用本文的开关流图模型仅需34 s，而使用Simulink/Simpowersystem的模型需471 s。使用开关流图建模仿真速度提升了10倍以上，也可以看出，流图模型稳态电压波动及加减载时电压响应与Simpowersystem的模型相差不大，可以用流图模型来进行更长时间尺度的仿真。为机电系统模式切换和故障动态过程的快速仿真分析提供了条件。

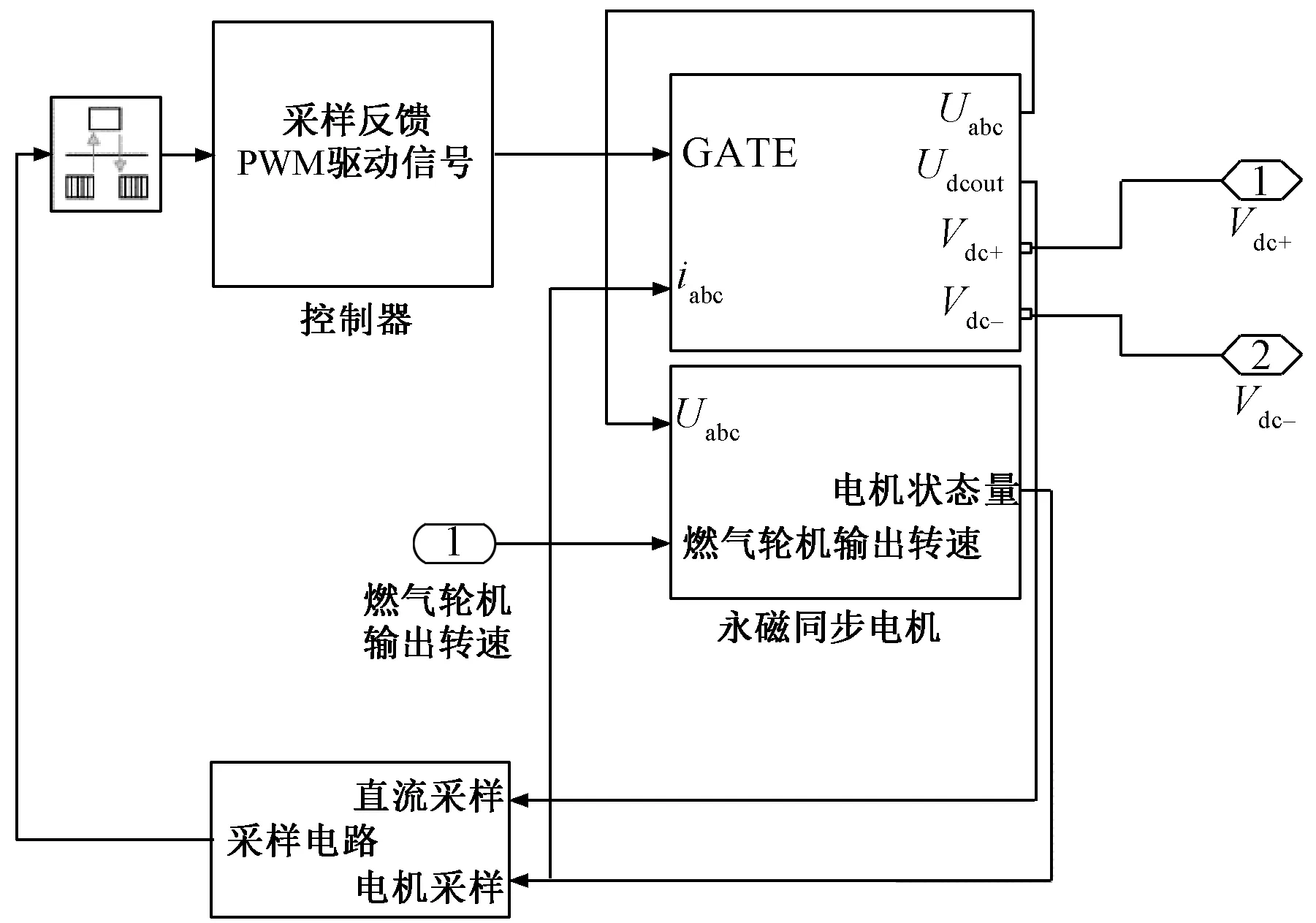
图12 发电机及电压源整流器的Simulink模型

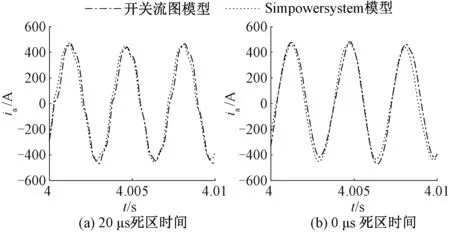
图13 Simpowersystem与开关流图的发电机整流器模型对应不同死区时间的a相电流仿真结果

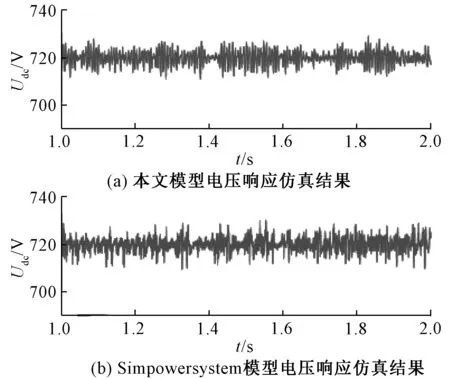
图14 Simpowersystem与开关流图的发电机整流器模型直流电压仿真结果

3.3 燃气轮机发电仿真验证

搭建了分轴微型燃气轮机Simulink模型及基于大信号流图的控制三相永磁同步电机的整流器和逆变器的Simulink模型。在Simulink中作加载及整流器封PWM脉冲等工况的仿真，得到燃气轮机转速响应及发电机电压电流响应。为了验证本文模型的有效性，在图 15的实验台上进行了相同工况的测试，微型燃气轮机的参数如表1所示。

图15 试验台架

以电阻作为发电机组负载，突加功率阶跃后负载电阻不变，由于发电机组采用可控整流方式工作，因此折算到燃机轴上的负载具有恒功率性质，由于燃机转速控制特性较软，突加负载Ps后其输出转速波动，引起转矩TL的随动波动，仿真结果如图16所示。

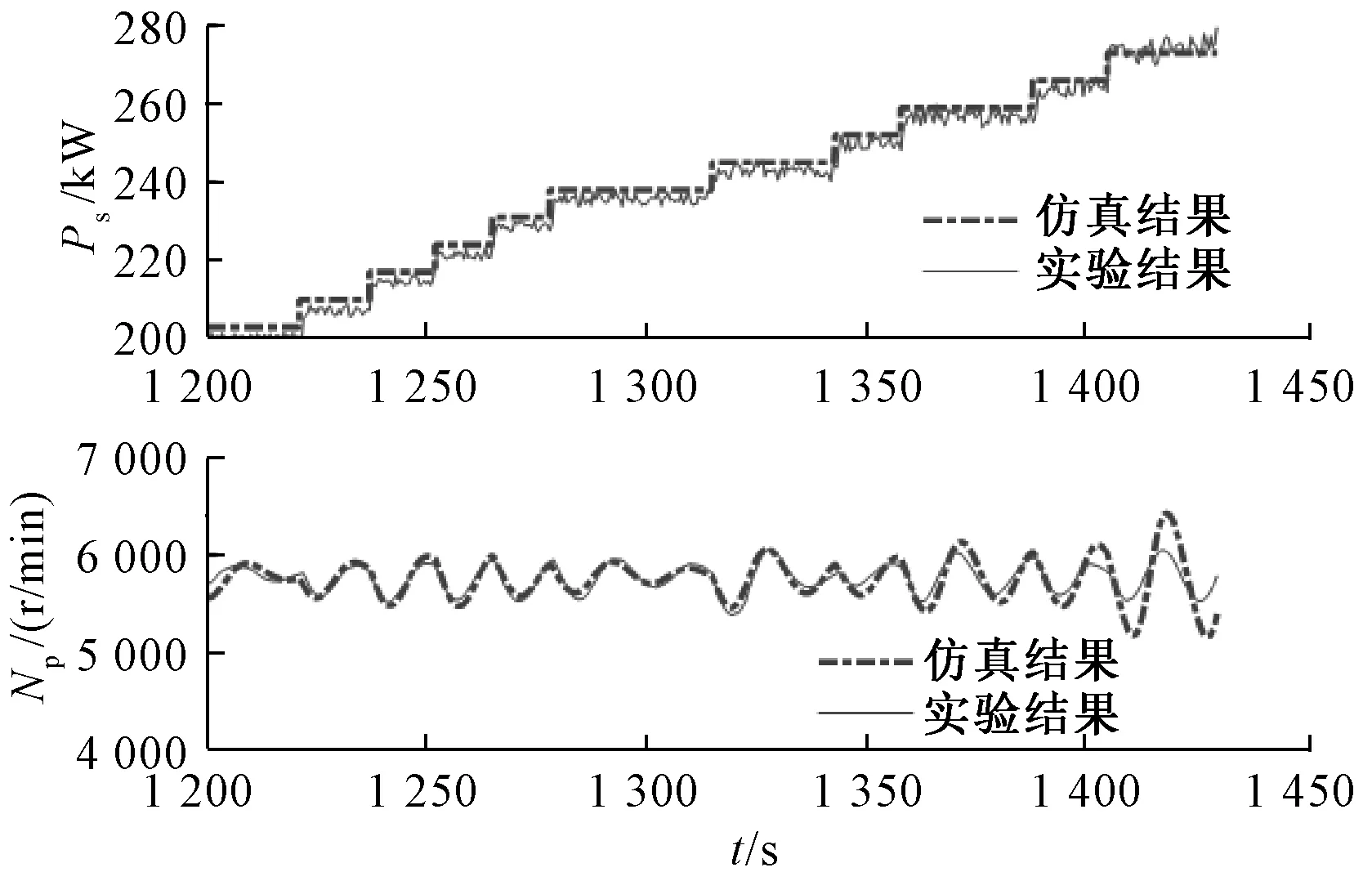
图16 燃气轮机LPT转速随负载变化仿真及实验结果

当系统功率较低时，燃气轮机调节能力足够，LPT速度Np稳定；当燃气轮机运行于额定功率点附近，Np在扰动下失去稳定。

在实验台上进行相同的测试。 所得结果如图16所示。系统加载过程中燃机转速响应与从模型仿真分析获得的结果非常接近。

在1 400 s时施加7 kW的负载扰动，LPT速度Np振荡，会进一步导致系统不稳定。 当不满足稳定性条件时，Np速度不稳定，这与实验结果相同。

为了验证模型在系统正常运行、故障中和故障重构后的有效性，对整流器故障进行仿真，整流器首先可控整流恒压发电运行，40 s时模拟发电机整流器故障封锁PWM脉冲，发电机组不控整流发电，整流器电压响应及燃气轮机动力涡轮转速响应仿真结果如图17所示。在故障时，整流器不控发电，电压降低，由于负载为电阻负载，发电系统负载功率降低，燃气轮机动力涡轮上升到6 200 r/min，最终由于燃气轮机转速控制器作用，转速稳定在5 800 r/min，与实验结果一致。

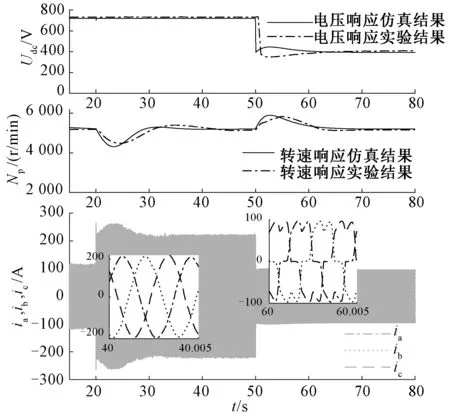
图17 整流器封波保护时电压及燃气轮机动力涡轮转速响应

4 结论

本文改进了分轴微型燃气轮机的线性化模型，根据不同工况、不同频率下的实测数据对微型燃气轮机关键参数进行抽取，提出一种适用于故障及扰动分析的微型分轴燃气轮机模型和PWM整流器流图模型。所提出的模型可以在考虑电力电子装置微观动态过程的前提下实现完整的机械系统的时间尺度过程的仿真，可兼顾整流器正常运行、故障中和故障重构后对燃气轮机发电系统的仿真分析。

仿真结果表明，所提出的模型能够体现燃气轮机的动态特性和整流器的开关特性，通过与Simulink/Simpowersystem模型仿真结果对比，验证了本文仿真模型的有效性。所提出的模型的仿真结果与实验结果对比也表明，该模型能够反映燃气轮机发电系统在加减载及故障时的动态响应，为混合动力系统的软硬件设计及故障保护策略设计等工作提供了较为精确的数学模型及仿真分析方法。