一种基于冻结磁导率的高频变压器直流偏置电流计算方法

田 煜， 金 平

(河海大学能源与电气学院， 江苏 南京 211100)

1 引言

近年来，可以实现电能灵活转换、具有高功率密度和可调电能质量等优点的电力电子变压器(Power Electronic Transformer，PET)受到广泛关注，为智能配电网的实现提供了良好的研究基础[1-3]。高频变压器是PET的核心部分，研究发现，电力电子变换器部分开关器件使用过程中会出现以下问题[4]：①开关特性参数的不一致性；②驱动控制系统脉冲宽度的不一致；③一段时间内的终端直流电压的变化；④闭环控制系统得到的移相比的调整等非理想行为，会使变换器出现上下半桥不对称运行，或者并联运行产生环流等现象，并进一步导致高频变压器一次侧输入绕组中产生直流电流，发生变压器的直流偏磁现象，不但影响传输效率，还会引发安全事故。

直流偏磁现象会对各种器件产生诸多不利影响。对于地磁感应引起的直流偏置电流，文献[5]分析了其对于电流互感器的影响，文献[6]和文献[7]分别分析了其对于变压器饱和及其差动保护的影响，并对变压器谐波、铁心过热，绕组损耗增加以及保护装置误动作等现象进行了研究。文献[8]指出磁饱和电抗器在直流偏磁下会发生电磁振动并产生噪音。文献[9]研究了直流偏磁对单相变压器铁心磁通和磁阻的影响。

为了减小直流偏磁带来的不利影响，一些学者开始研究直流偏磁的抑制措施，常用的方法主要有中性点串联电阻限制直流电流值[10]，中性点串联电容阻断直流通路[11]，中性点注入反向电流抵消直流电流[12]。文献[13]对几种抑制变压器中性点直流电流的方法进行比较，并指出主变中性点装设电容器是抑制并消除流过主变中性点直流电流的最优方法。

工频变压器的直流偏置电流的计算多采用J-A法[14]、B-H曲线族[15]等方法，这一类方法往往需要在变压器不同的工作点和输入电流情况下测试，并做针对性的系数拟合，且不同的变压器均需要单独进行实验测试和拟合，计算量和现场测试难度较大，也不适合电力电子变压器种类繁多的现实状况；同时，高频变压器的工作频率相对较高，往往采用铁氧体磁心，有别传统变压器采用硅钢片的工频磁化曲线，磁化曲线的工作状态也比较复杂，采用传统工频变压器的模型，系数拟合的难度显著增加。对于高频变压器中的直流偏置电流，目前主要有测量和预测计算两种方法。文献[16]提出一种利用一次和二次绕组电流测量直流偏置电流的方法。文献[17]提出一种新型传感器用于检测直流电流分量。测量法对仪器和实验精度要求高，实现往往比较困难，所以直流偏置电流预测方法的提出非常必要。文献[18]通过对零电压开关(Zero-Voltage Switched，ZVS)变换器伏秒失配补偿电路分析，提出一种计算直流偏置电流的方法。文献[19]和文献[20]提出了考虑半导体开关和驱动信号的不一致性直流偏置电流的预测方法。然而，这些现有的高频变压器直流偏置电流的计算方法都只适用于某一具体电力电子电路，没有直流偏置电流计算的通用方法。

冻结磁导率方法(Frozen Permeability Method，FPM)一般用于饱和铁心材料的磁场中，为非线性问题提供了线性分析的方法。文献[21]利用FPM精确地分离电机中由自通量和相互通量引起的转矩，文献[22] 将FPM用于分离平均转矩，文献[23]从仿真和实验的角度讨论了FPM用于永磁电机中磁通量的分解。目前，冻结磁导率的方法大多用于电机的磁场中，还没有被用于其他含铁心的设备中。

本文将冻结磁导率技术用于高频变压器，提出一种高频变压器直流偏置电流的通用计算模型，该模型与传统的偏置计算相比，取消了偏置工作点附近的磁环曲线的系数拟合过程，为获得直流偏置电流提供一种简便的计算方法。通过分解饱和磁场的交流分量和直流分量，建立了一次侧和二次测的对应关系，在此基础上，在铁磁材料的非饱和区引入矫正系数，实现从二次侧电压直接预测一次侧直流偏置电流，并通过直流偏磁实验验证该计算模型有着良好的精度。

2 直流偏磁预测模型

2.1 冻结磁导率的原理

冻结磁导率原理图如图1所示，f(H)为Mn-Zn铁氧体在2 kHz的基本磁化曲线，对其进行方程拟合，得到以场强H为变量，以磁通密度B为函数的基本磁化曲线的拟合方程。

(1)

式中，ci(i=1～5)为拟合系数。

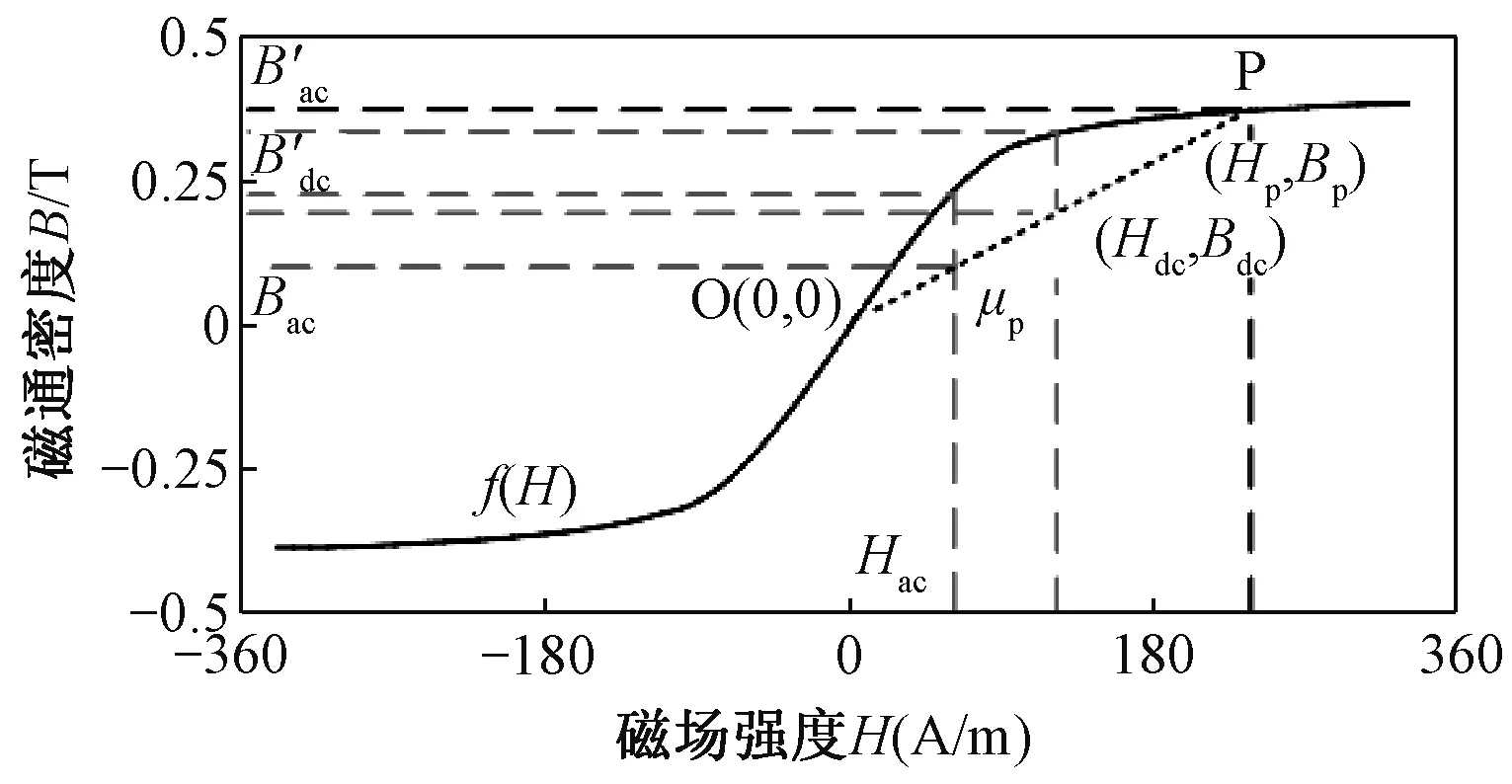
图1 冻结磁导率原理图

当铁心中没有直流偏磁时，H和B构成的磁滞回线应该关于原点O(0，0)对称，H和B的最大值和最小值也应该关于O对称。当存在直流偏置电流，变压器一次侧电流含直流分量idc和交流分量iac，一次测电流i1=iac+idc。相应的场强直流分量和交流分量为Hdc和Hac。

(2)

总场强如下：

H=Hac+Hdc

(3)

式中，n1为一次侧绕组匝数；l为有效磁路长度。显然，此时H和B的最大值和最小值将不再对称。

首先假设可以忽略磁滞回线的影响，这一点将在2.3节中单独进行讨论，当发生直流偏磁时，仅考虑直流偏置电流时，铁心的工作点设为P(Hp,Bp)。为了简化分析，假设发生直流偏磁时，励磁电流只含有直流分量和基波的周期的分量。此时，场强H也只包含直流分量和基波的周期的分量。根据冻结磁导率的方法，将P点的磁导率μp冻结，场强与磁通密度的关系可以表示为：

(4)

式中，Bac和Bdc分别为磁通密度的交流分量和直流分量。

在P点附近，基本磁化曲线近似为一条直线，f(H)的导数为常数。

(5)

2.2 不考虑滞环情况下的二次侧反电动势

按照冻结磁导率原理，电流线性变化时，磁密的直流分量与交流分量分别为：

(6)

(7)

(8)

式中，f(Hdc)为与场强直流分量Hdc对应的磁通密度定值。

因此，式(6)需要修改为：

(9)

不同材料的铁心在不同频率下基本磁化曲线不同，为了计算方法的准确性，需要进行磁心的磁性能实验，找到对应的基本磁化曲线方程。

测量得到的数据需先通过移动平滑滤波器进行平滑处理后再进行多项式拟合。由于整体拟合的不准确性，本文采用分段拟合的方法对铁心的基本磁化曲线进行拟合。拟合后的基本磁化曲线方程可以表示为：

(10)

式中，I、II和III分别表示-5.4≤i<-1.54、1.58≤i<5.2和-1.54≤i<1.58三个电流区间。

假设一次侧电流只包含直流分量和基波交流分量，即i1=a0+a1cos(ωt)，其中a0为直流偏置电流，a1为输入交流电流的幅值，代入安培环路定律，可得到场强

(11)

将式(11)代入式(10)，考虑到二次电压以基波为主，将所有H的高次幂展开，只保留基波项。此时，Hλ(λ=1、2、3、4)的基波系数如表1所示，磁通密度B随时间变化的函数可以表示为：

(12)

式中，c14、c25、c35均为常数，分别表示不同区间下的f(Hdc)。

表1 基波项系数

根据电磁感应定律，二次侧反电动势交流值和a0、a1的关系可以表示为：

(13)

2.3 考虑滞环的影响

图2为考虑滞环情况下计算方法的矫正原理，当正弦电流最大值为imax并且没有直流偏磁的情况下，磁滞回线为a曲线。假设存在一个含直流偏置的正弦电流，电流最大值imax和最小值imin分别对应于图2中的Hmax和Hmin，磁滞回线b曲线。可以看出，Hmax位置可以直接采用基本磁化曲线，Hmin位置需要考虑磁滞回线的的的影响。

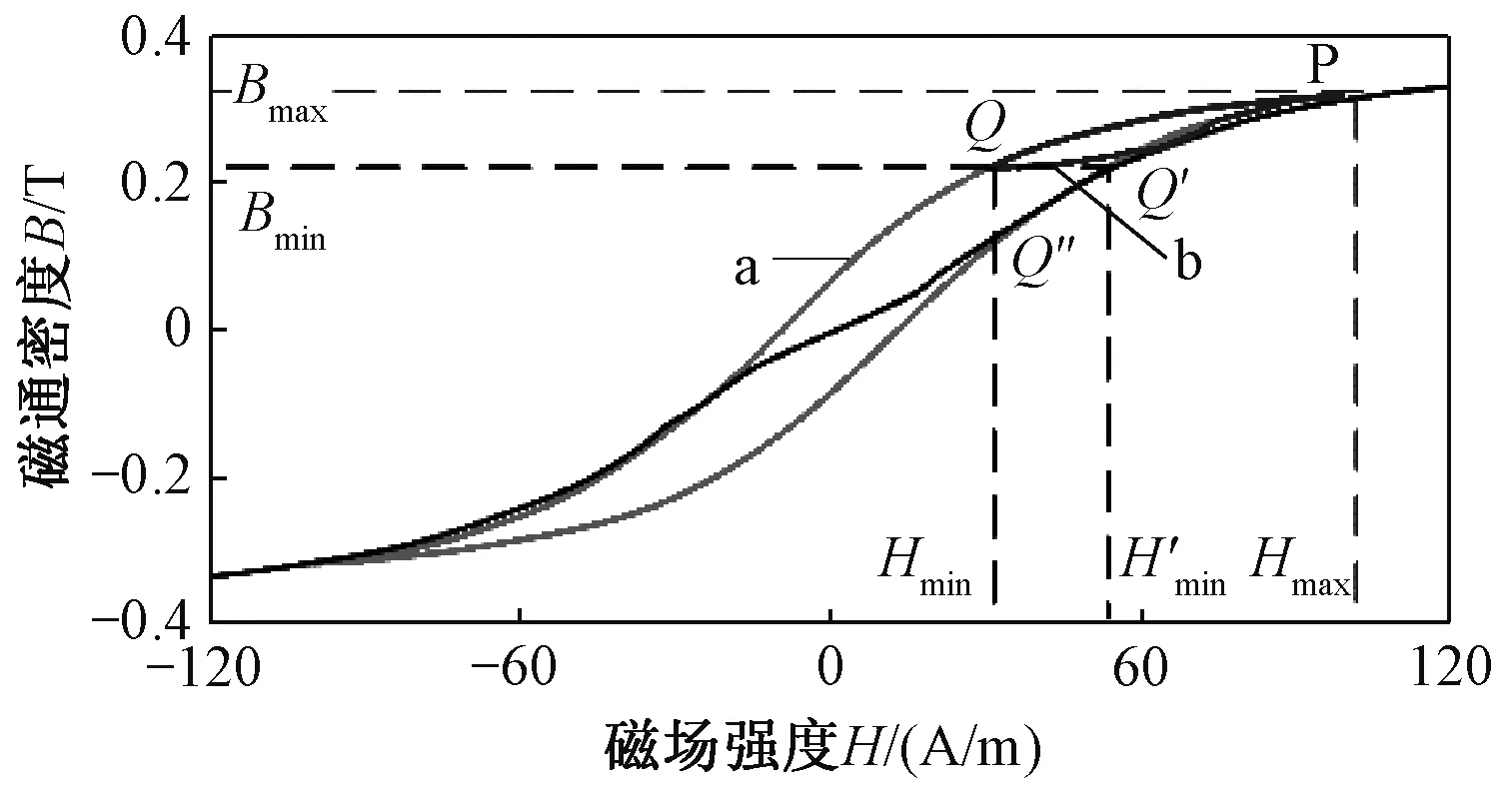
图2 非饱和区模型矫正原理图

(14)

以磁通密度为变量的基本磁化曲线方程：

(15)

则场强矫正系数L可以表示为：

(16)

(17)

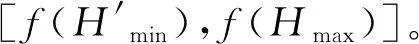
(18)

将式(5)、式(11)代入式(18)得：

(19)

根据电磁感应定律，考虑滞环后二次侧反电动势交流值可以表示为：

(20)

(21)

3 实验测量与验证

3.1 实验测量原理

图3所示为本文直流偏磁实验系统的原理图，图4所示为用于测试直流偏磁的实验平台。通过信号发生器(Tektronix AFG3021C)和功率放大器(Aigtek ATA-L8)为实验线圈的一次侧提供交流电流iac=Iaccos(ωt)，直流电源(LODESTAR LP305DE)提供直流偏置电流idc。示波器(Tektronix MDO3024)测量二次侧电压反电动势e和一次侧电流i1。

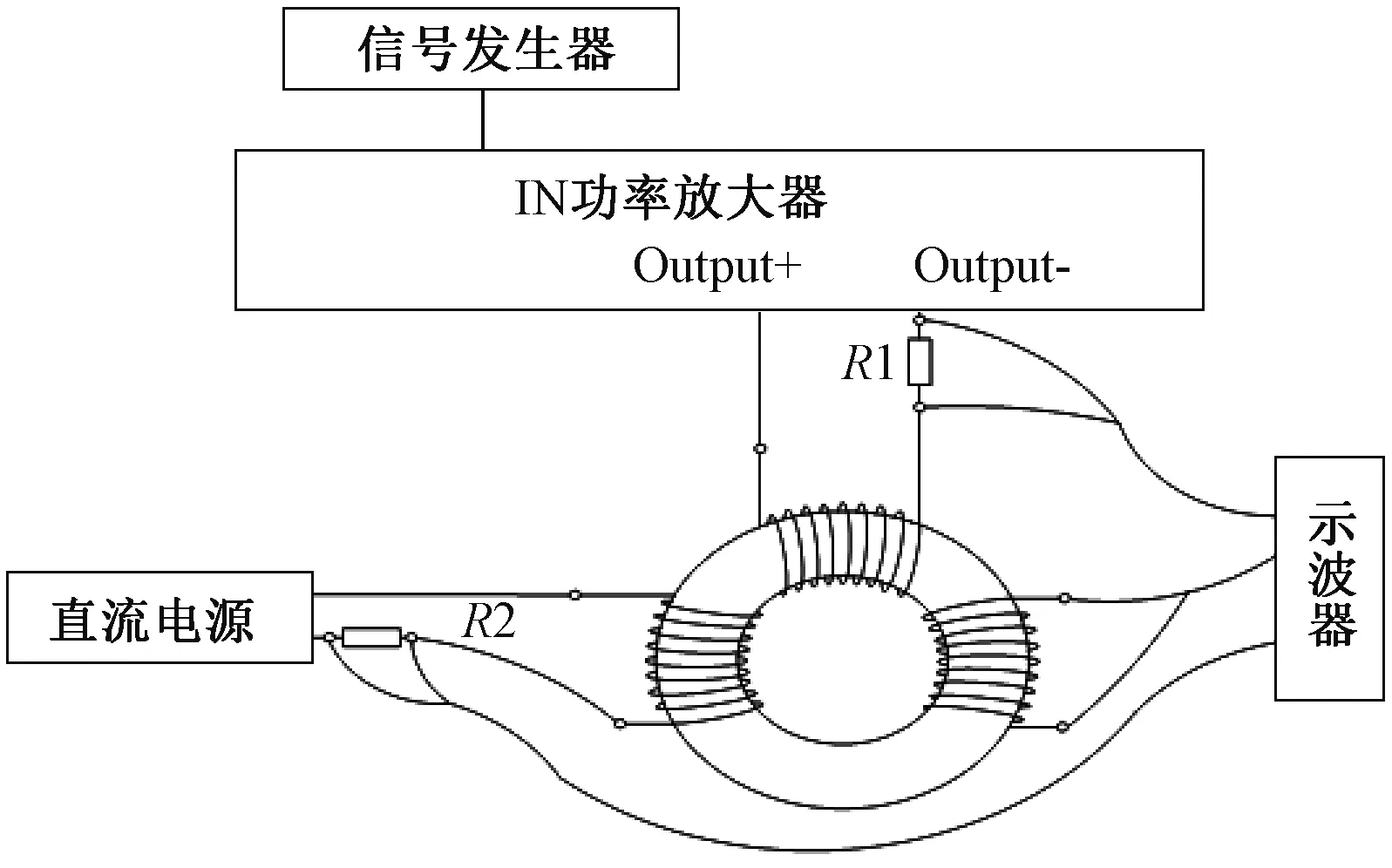
图3 实验测量原理图

图4 实验平台

3.2 实际测量与计算结果对比

在实验过程中，可以对场强进行计算，也可以对磁通密度进行计算。对场强进行计算时，通过测量不同一次侧直流偏置电流情况下二次侧空载反电动势，可以对铁心场强进行计算，计算结果与通过一次侧电流测量得到的铁心场强H进行比较。对磁通密度进行计算时，通过测量不同一次侧直流偏置电流情况下的一次侧电流，对铁心磁通密度进行计算，计算结果与通过二次侧空载反电动势测量得到的铁心磁通密度进行比较。理论上，两种方法是等效的，本文选择对磁通密度进行计算的方法，验证本文的计算过程。

对磁通密度进行比较时，由于变压器只能传递交流信号，所以二次侧空载反电动势的大小只受一次侧交流电流的影响，直流偏置电流的作用使铁心在较小的交流电流的作用下就会饱和，因此二次侧空载反电动势会出现感应电压幅值小、畸变严重的情况，则相应的磁通密度B也会小，此时的磁通密度B并不是该情况下实际的磁通密度，而是用峰峰值来表示磁通密度变化范围大小。一次侧电流采用计算模型计算磁通密度B，需去除直流偏置电流(常数项)的影响。比较两个磁通密度的峰峰值来验证本文计算过程的精确度。

3.2.1 不考虑滞环时直流偏磁计算

图5为某一深度饱和情况下的磁通密度的交流分量Bac的实际值、不含谐波的计算值和含谐波的计算值对比图，具体误差对比如表2所示。

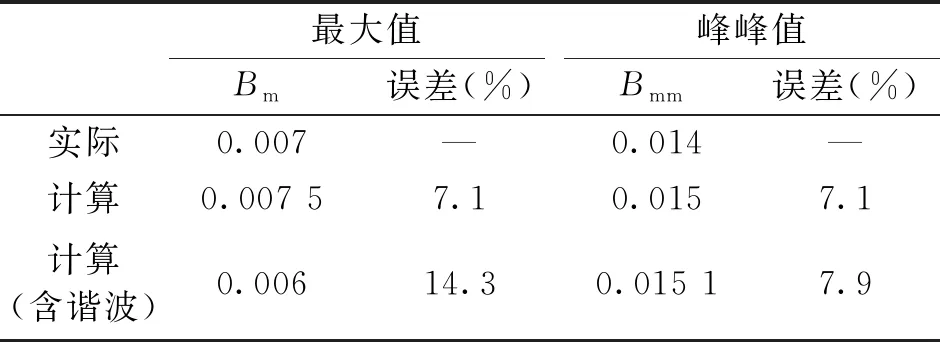
表2 有无谐波的计算模型误差对比

由图5和表2可看出在不考虑滞环时含谐波的计算方法虽然在峰峰值上也有不错的计算，但是从波形的重合情况来看，谐波的存在对磁通密度B值的瞬时计算影响较大；而去掉谐波的计算方法不但有较好的瞬时计算能力，且也有较小误差，具有更精确的计算效果。

不考虑滞环的计算方法在交流电流幅值Iac=0.3、0.5、1时磁通密度随直流偏置电流Idc的变化情况如图6所示，误差变化趋势和数据对比如图7所示。

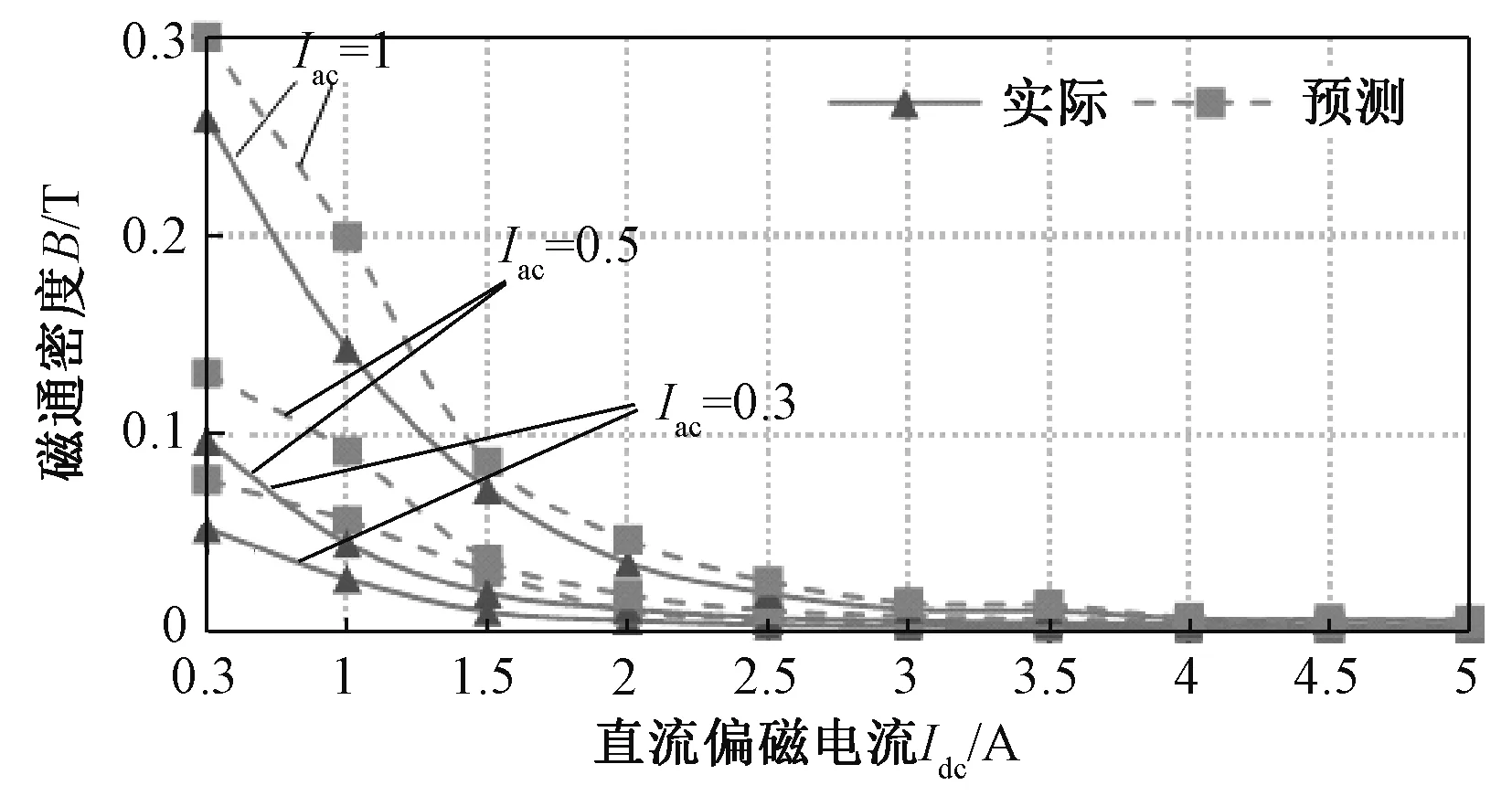
图6 Iac=0.3、0.5、1时最大磁通密度随直流偏磁的变化曲线

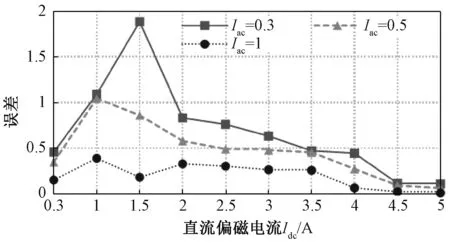
图7 Iac=0.3、0.5、1时误差随直流偏磁的变化曲线

由图6的变化趋势可知，随着直流偏置电流Idc的增加，实际和计算值的差值逐渐减小，误差也逐渐减小。

根据图7的误差曲线变化趋势可知，输入正弦电流的幅值越大，计算的精确度越高；随着Idc值的增大，饱和程度越高，计算的精确度也越高。也可看出，计算方法在饱和区有较精确的计算，但若用在非饱和区域会产生较大的误差，与原理分析相符，因此为了提高在非饱和区域的精确度，需要对不考虑滞环的计算方法进一步的矫正得到在非饱和区域的计算方法。

3.2.2 考虑滞环时的直流偏磁计算

由于在Iac=0.3时，不考虑滞环的计算方法误差最大，所以以Iac=0.3时的情况为例进行校正。经过矫正系数矫正后，不考虑滞环的计算方法矫正前、矫正后以及实际的磁通密度对比情况如图8所示，误差对比如图9所示。

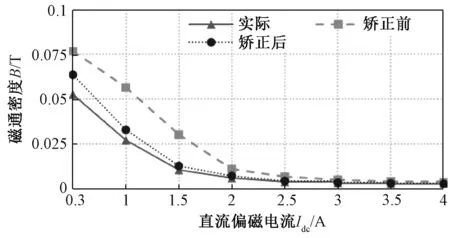
图8 Iac=0.3时计算模型矫正前、矫正后和实际值对比

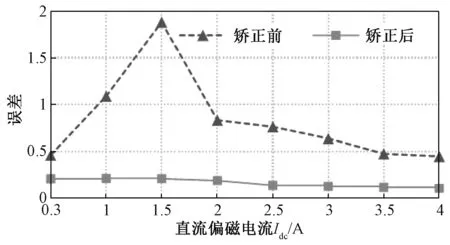
图9 Iac=0.3时计算模型矫正前、矫正后误差对比

由图8和图9可看出，矫正后的计算值相较于矫正前，精度有了很大程度的提高，且矫正后的精确度随着饱和程度的加深而提高，误差最小为10%左右。

图10为不同Iac情况下，校正系数K随直流偏磁Idc的变化情况，由图可看出，交流电流幅值Iac越大，K值越小。利用该曲线还可查找这几种情况下的矫正系数K，与图6结合对直流偏置值做简单快速的计算。

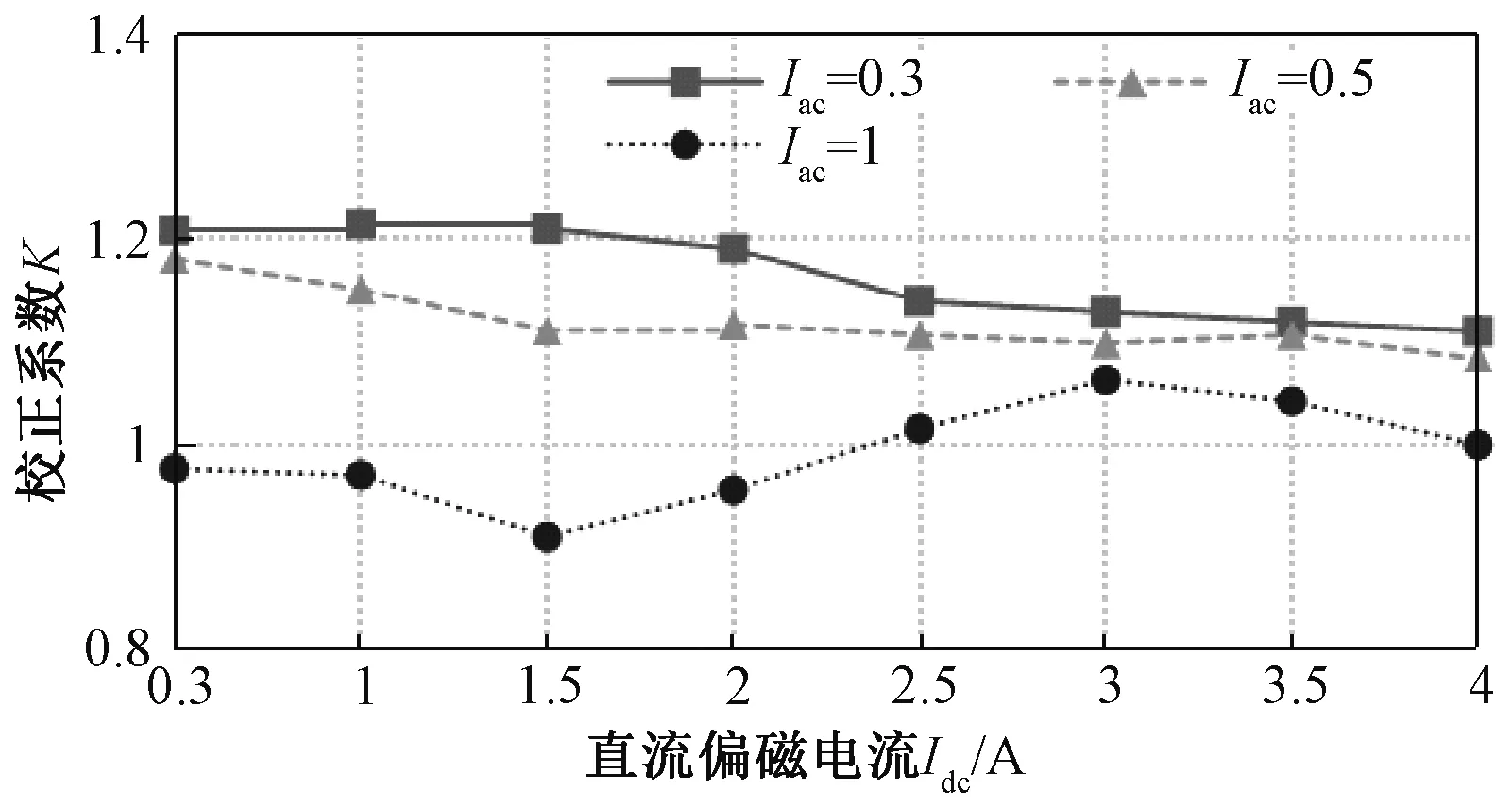
图10 Iac=0.3、0.5、1时枝正系数K随直流偏置的变化曲线

本文的实验情况均为变压器空载，考虑到实际有负载情况时，由于研究的对象是磁心的磁特性，所以有无负载情况下都可用该模型进行直流偏置电流的计算。

4 结论

本文提出了一种区别于传统偏置计算方法的高频变压器直流偏置电流的计算方法。该计算方法是在冻结磁导率的方法和基本磁化曲线的基础上推导得到。通过建立一次侧和二次侧的对应关系，实现根据二次侧电压计算得到直流偏置电流的目的。由于滞环的影响，非饱和区的模型是在不考虑滞环的预测方法的基础上通过校正系数校正得到。本文除对计算模型的原理和推导过程进行详细分析之外，还进行了直流偏磁实验，来验证该模型的可行性和精确度。