考虑换流器外环特性的双馈风电场并网稳定性分析

孙 瑶， 韩民晓， 黄永宁， 张汉花

(1. 华北电力大学电气与电子工程学院, 北京 102206；2. 宁夏电力安全重点实验室， 国网宁夏电力科学研究院， 宁夏 银川 750002)

1 引言

随着新能源比例增大，换流器控制及其与电网交互作用引起的风电场并网稳定性问题得到了广泛关注，将在今后较长一段时间内持续威胁电网安全运行。为了定量分析影响因子对稳定性的作用，阻抗分析法得到广泛应用[1-4]，在时域系统中普遍使用序阻抗分析法，在复频域中使用dq坐标系下的阻抗模型。序阻抗分析法需要在时域中对电压电流进行傅里叶变换，基波量经dq变换得到直流量，扰动量经变换得到交流量，由功率计算式得到的波动功率都是零，所以现有序阻抗模型[5-13]仅用于研究换流器内环控制参数对系统稳定性影响的问题。因此为研究功率外环对风机并网系统的影响，必须模糊扰动量具体表达式，使用dq坐标系下小信号分析法可以研究功率外环以及直流母线上的功率波动量对阻抗模型的影响。

在现有研究中，文献[8]建立了只考虑转子侧换流器(Rotor-Side Converter, RSC)参数影响的风机阻抗模型。文献[9]建立了考虑RSC与电网侧换流器(Grid-Side Controller, GSC)的风机模型，指出由于GSC等效阻抗较大，且为输入阻抗电路的并联支路，所以忽略了GSC控制器参数对输入阻抗的影响。实际上，在不稳定状态时，RSC侧波动会通过直流环节传递至GSC，若要建立完整的风机阻抗模型，考虑两侧换流器以及直流环节是有必要的。文献[10,11]考虑了励磁互感，在静止坐标系中建立了风机模型，但依然忽略了GSC支路。以上研究均只考虑内环控制，而风机换流器一般采用双环控制，由于外环控制时间常数较大而被忽略，但对于建立用于分析中低频段的阻抗模型，外环是有必要考虑在内的。文献[14]考虑外环建立的模型可以较准确反映风机低频段的阻抗，但仍未完整考虑其他电路部分。现用于分析风电场并网稳定性的阻抗模型多数只考虑内环以及锁相环，无法准确体现风机阻抗的低频部分，也无法直观分析电网、控制电路以及电机两两之间的交互作用。而对于稳定性分析，只有在准确的阻抗模型下，才可以定量分析各控制系数在不稳定状态下的参数范围。

本文在dq坐标系下建立了考虑了风机、包含RSC与GSC及其锁相环(Phase-Locked Loop, PLL)、直流环节的换流器控制回路、出口滤波器和变压器的双馈风机(Double Fed Induction Generator, DFIG)阻抗模型。利用宁夏麻黄山风电场风机实际参数建立模型，对比了各部分对风机阻频特性的影响，证明考虑直流环节以及PLL对风机阻抗模型的必要性。最后用广义奈奎斯特稳定判据分析各系统参数对风机并网稳定性的影响，找出具体影响稳定性的参数范围，并用宁夏电网麻黄山双馈风电场仿真算例验证其正确性。

2 DFIG阻抗建模

为在dq坐标系下建立DFIG阻抗模型，需要得到风机出口电压与电流的关系，其中各处电压电流关系，如图1所示。

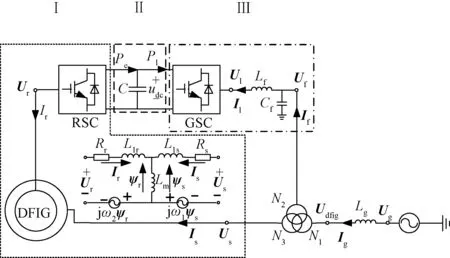
图1 DFIG电压电流关系示意图

其中，Ur与Ir、Us与Is分别为转子、定子的出口电压与电流，Ul与Il、Uf与If分别为GSC出口、经滤波器出口的电压与电流，Udfig与Ig分别为DFIG出口电压与电流，Ug为电网电压。

为研究风电机组本身对电网次同步振荡的影响，利用小信号线性化法建立包含风机主电路与换流器控制电路的阻抗模型，能够用于分析DFIG并网系统中各参数对系统稳定性的影响。用小信号分析法进行线性化，统一用式(1)矩阵形式表示。

(1)

式中，x为任一dq坐标系下的矩阵变量；X为稳态初值；Δx为小信号矩阵变量。

2.1 考虑定转子关系的RSC模型

DFIG等效电路如图1中Ⅰ框所示。定转子均采用电动机惯例。定子同步角频率为ω1，转子旋转角频率为ωr，转子参数均已折算至定子侧，折算后定、转子绕组匝数相同。

定转子电流电压小信号模型为：

(2)

其中

式中，ω1为定子角频率；ω2为转差角频率；Lm为定、转子同轴等效绕组间的互感；Ls为定子等效两相绕组自感；Lr为转子等效两相绕组自感；L1s、L1r分别为定、转子漏感。

转子侧控制回路采用双环解耦控制方式，如图2所示,其中σ=1-Lm2/(LsLr)为电机漏磁系数，Hn为内环PI环节，Hw为电流外环控制环节。下标s代表定子出口电气量，下标r代表转子出口电气量，ref代表计算所得或给定的参考值。

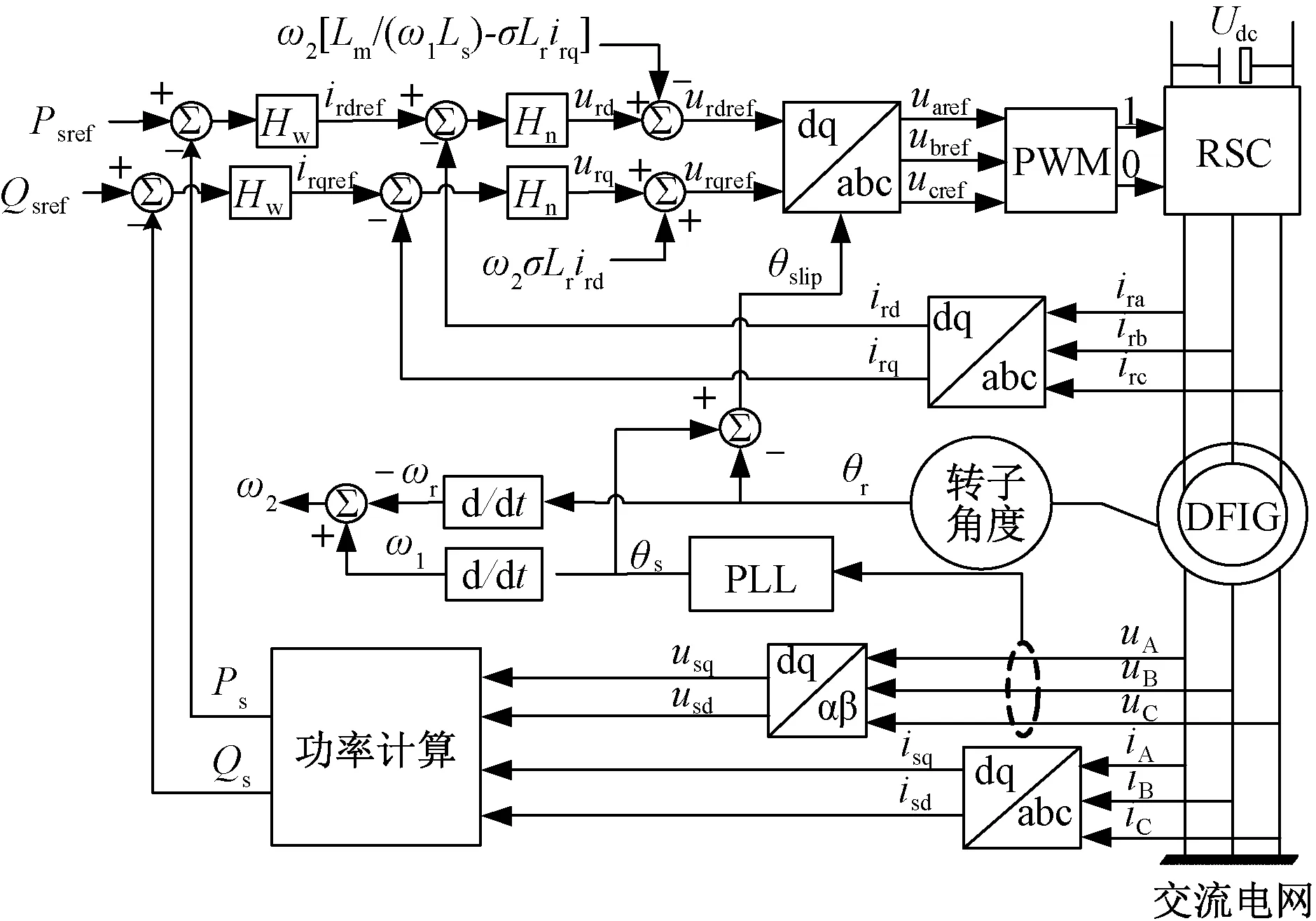
图2 RSC的矢量控制框图

内环电压参考值为：

Δurref=Hnn(Δirref-Δir)+GddΔir

(3)

其中

外环为PQ解耦控制，电流参考值为：

(4)

其中

式中，U、I分别为系统稳定运行状态下的电压、电流值。

PLL可以将电网波动传递至控制回路，其中PLL的传递函数为：

(5)

式中，HpLL=Kpp+Kpi/s为锁相环PI环节传递函数。

电网电压扰动后的定转子电压与电流为：

(6)

式中

综合式(3)、式(4)、式(6)得到转子侧控制电路等效阻抗表达式，再由式(2)消去定子电流，可以得到转子侧控制器小信号阻抗模型。

Δur=ZRSCΔir+KusrΔus

(7)

其中

式中，ZRSC为转子侧控制电路等效输入阻抗；Kusr为定子电压通过PLL的交互作用对转子电压的影响系数，其与稳态工作点、RSC与PLL的控制参数、电机电路参数有关。

2.2 考虑直流环节的GSC模型

直流环节在正常工作状态下可以起到电气隔离的作用，但在次同步振荡状态下，直流环节会成为转子侧控制回路与网侧控制回路波动传递的桥梁。直流环节如图1中Ⅱ框所示，udc为直流电压，Pe为转子侧有功功率，Pl为网侧有功功率，功率守恒公式经小信号线性化写成矩阵形式：

(8)

其中

GSC出口电路如图1中Ⅲ框所示，电压(KVL)等式经小信号线性化得：

Δul=Δuf-GzlΔil

(9)

其中

电流(KCL)等式经过小信号线性化写成矩阵形式：

Δif=GzcΔul+Δil+GclΔil

(10)

其中

GSC通常采用双环控制，外环控制直流电压和无功，内环控制电流，GSC的矢量控制框图如图3所示。当GSC零无功运行时，igqref=0，其中Hp为d轴电流内环控制环节，Hq为q轴电流内环控制环节，内环电压参考值矩阵形式为：

Δulref=Hpq(Δilref-Δil)+Δuf+GccΔil

(11)

其中

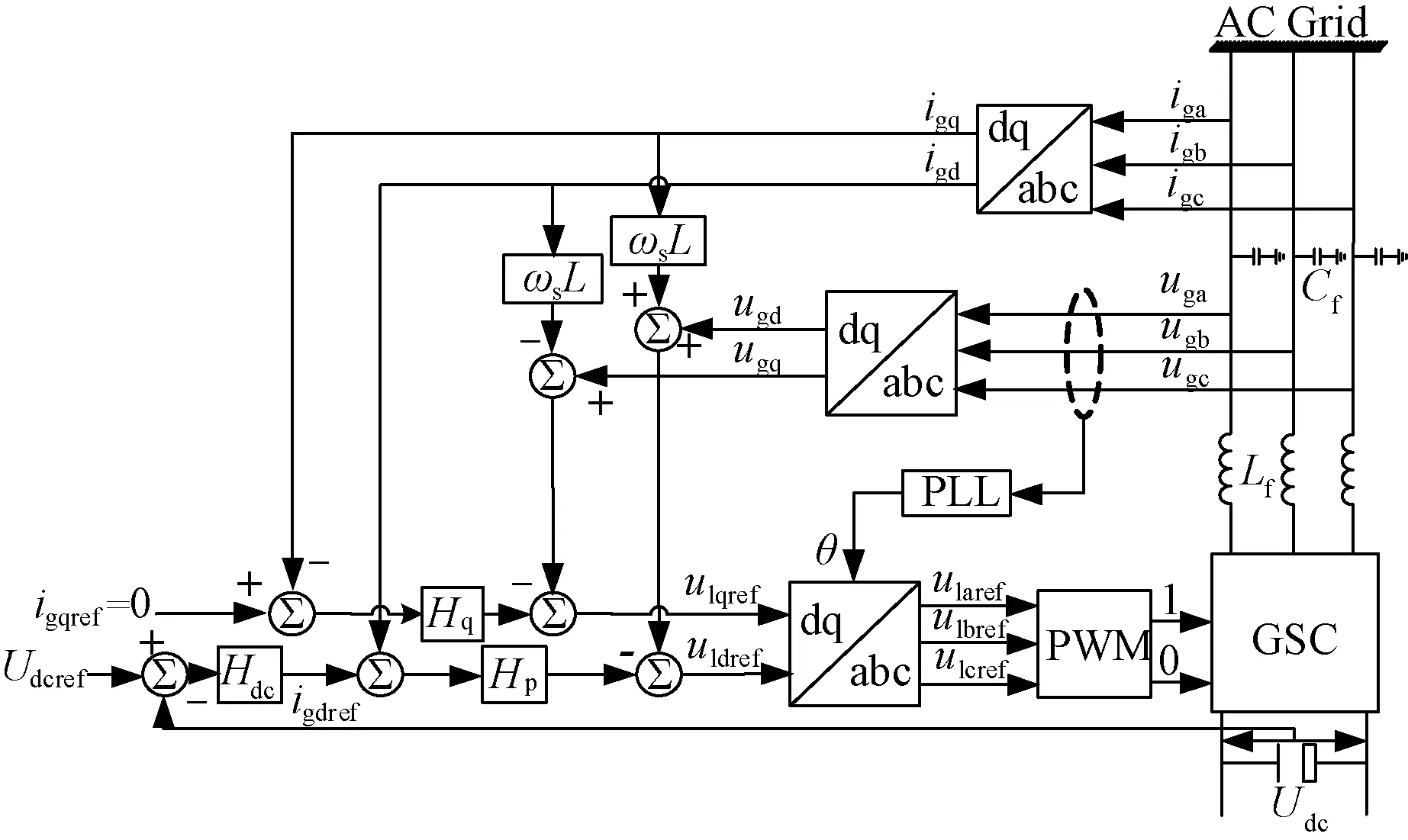
图3 GSC的矢量控制框图

经直流电压外环控制，得到电流参考值：

Δilref=Hdc0Δudc

(12)

其中

电网侧PLL与转子侧影响方式相同，都是联系电网电压与内部控制的中介，所以电网电压波动会造成控制电路内部波动，受PLL干扰的电网电压、GSC出口电流与最终输出的出口电压分别为：

(13)

其中

综合式(10)、式(12)、式(13)得到电网侧控制电路等效阻抗表达式，再由式(9)消去电网电压，可以得到电网侧控制器小信号阻抗模型。

(14)

将式(8)代入消去式(14)中的直流电压小信号量，得到GSC出口电压与电流的表达式。

Δul=ZGSCΔil+KuslΔus+KurlΔur

(15)

其中

GSC出口电压由网侧阻抗决定，受定转子电压影响，影响系数由网侧控制电路内外环与PLL控制参数、直流环节波动以及稳定工作点决定。

通过上述关系式推导，可以得到DFIG等效电路，如图4所示。

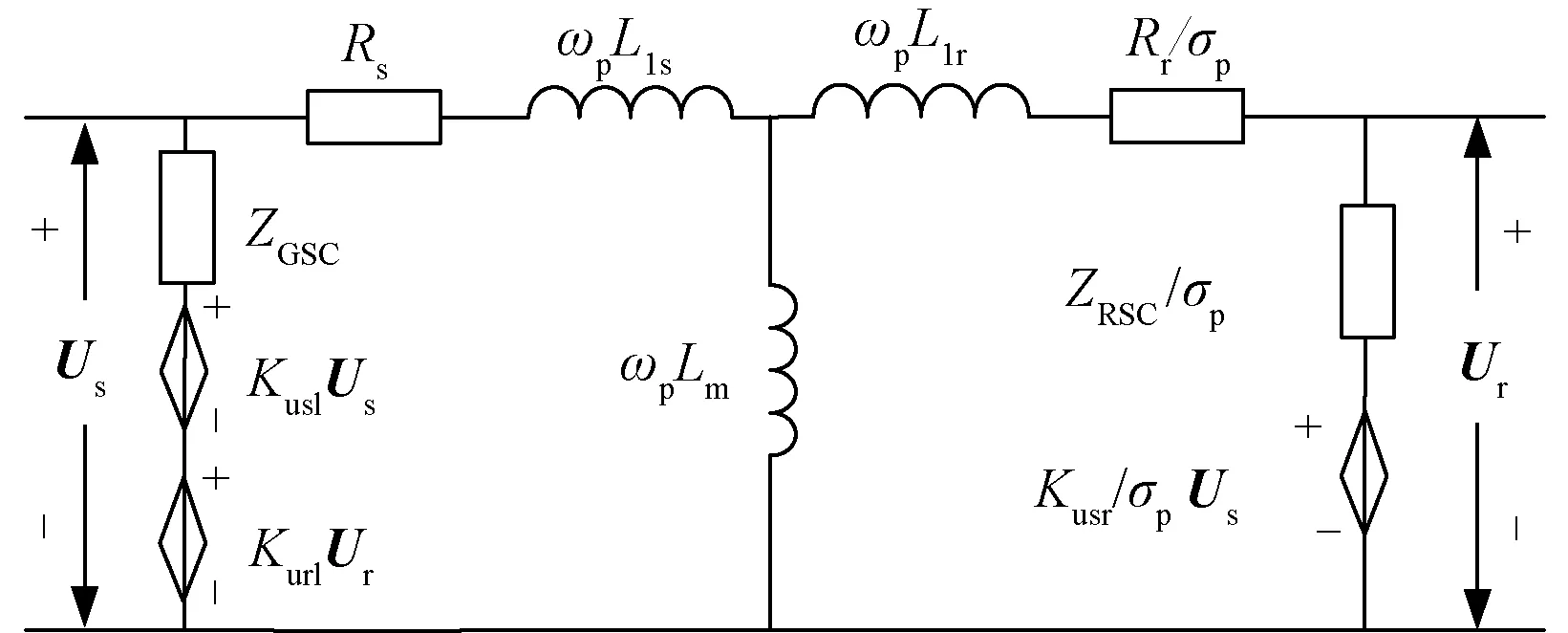
图4 考虑换流器的DFIG等效电路

2.3 考虑滤波器与变压器的阻抗模型

由于变压器的存在，电压电流存在倍数关系：

(16)

结合式(2)、式(7)消去转子侧出口电流，可得定子电流与电压的关系：

Δis=[Gzs+Gzms(ZRSC-Gzr)-1Gzmr]-1·

[E+Gzms(ZRSC-Gzr)Kusr]Δus=YsΔus

(17)

由此得到定子电流与电压的关系，为定子支路输出导纳，包含DFIG与RSC，记为Ys，即为图1上Ⅰ框中部分的出口导纳。

结合式(2)、式(7)、式(9)、式(10)、式(15)、式(16) 可以得到GSC支路经过滤波器的输入电流与并网电压的关系，并记换流器支路输出导纳为Yf，即为图1上Ⅲ框中部分的出口导纳，Ⅱ框中直流环节是两个部分之间传递波动的桥梁，此部分已经归算至网侧导纳中。

(18)

式中，Ksr为转子电压与定子电压的比例系数；Ksl为GSC出口电压与定子电压的比例系数。

因此，结合式(16)可以得到考虑换流器控制电路、网侧出口滤波器以及箱变后的DFIG等效输入阻抗为：

(19)

3 DFIG阻抗对比分析

本节采用Bode图分析PLL、直流母线和外环对DFIG阻抗模型的影响。依照宁夏市麻黄山双馈风机设计参数，在PSCAD中建立麻黄山第四风电场的仿真算例，250台双馈风机，经三级升压变压器，从0.69 kV升至35 kV，再经总线升压器，从35 kV升至363 kV，再经架空线路并入大电网，线路等效电阻为0.03 pu，等效阻抗为0.5 pu。

其中风电机组参数见表1。

根据式(23)中DFIG等效阻抗表达式，代入PSCAD中仿真所得运行参数，先经Matlab计算考虑控制电路内环外环、PLL以及直流环节的完整DFIG阻频特性，再分三种情况，依次不考虑直流环节、不考虑PLL、不考虑外环控制，画出各种情况下的dd、dq、qd、qq四象限阻频特性以及相频特性曲线，进行对比，如图5所示。

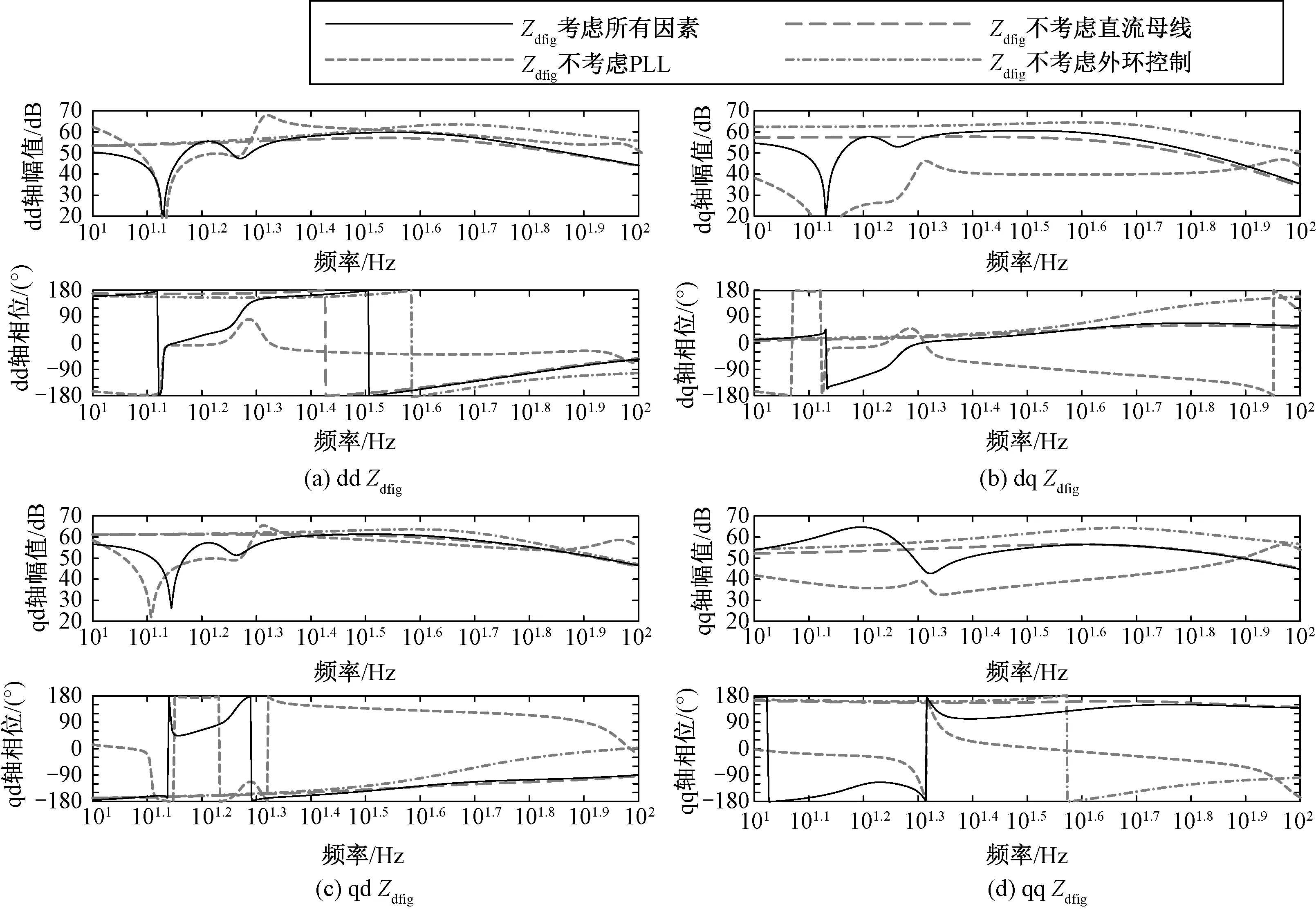
图5 风电场阻频特性曲线对比图

由图5可以观察到，若忽略外环控制与直流环节传递波动的影响，阻频特性中低频部分很大程度失真，负电阻范围也不同。直流环节影响反映在GSC直流外环控制中，直流环节是RSC中波动传递到GSC的桥梁，是影响风机阻频特性的重要因素。若忽略PLL，会影响风机阻抗正负性与容感性。由于该阻频特性曲线仅为现有仿真参数下的风机阻频特性，若需对风机并网进行稳定性分析，还需利用广义奈奎斯特稳定判据对各参数的影响范围进行分析。

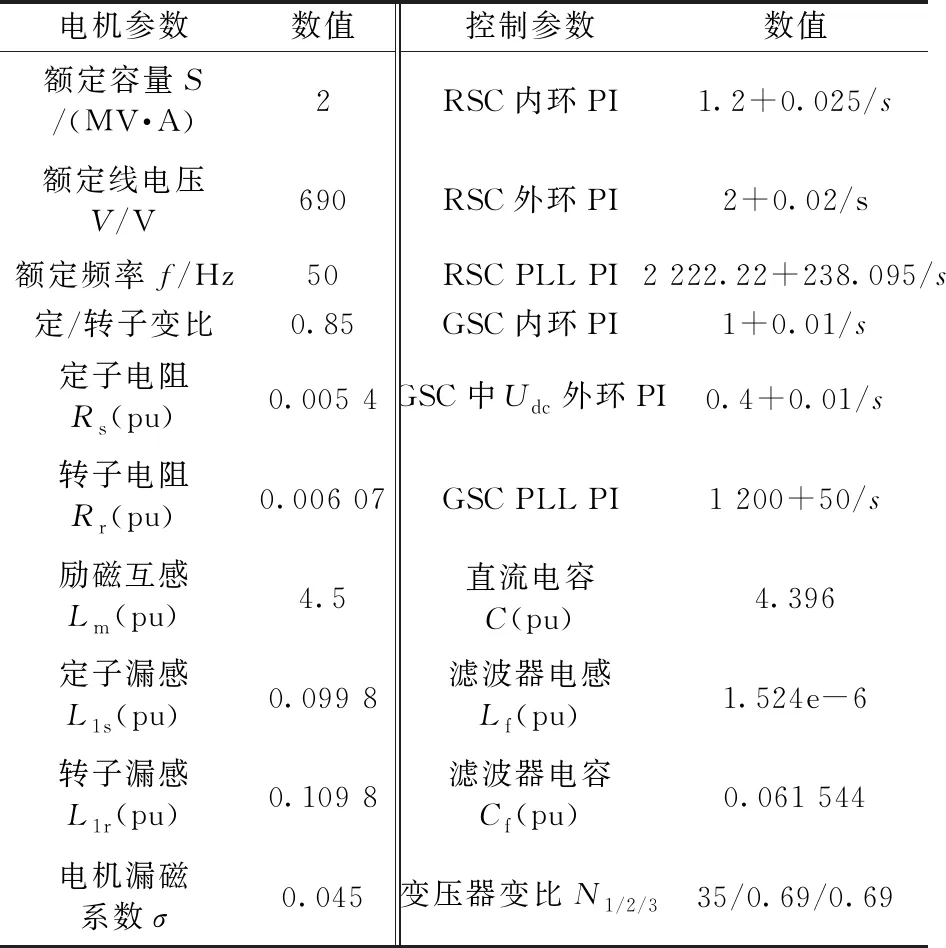
表1 风机仿真参数

4 DFIG并网稳定性分析

在dq坐标系下建立的风机并网系统阻抗模型为多输入多输出(Multiple Input Multiple Output, MIMO)系统，无法直接得到一般化的稳定运行区间，因此可以根据广义奈奎斯特稳定判据[15]进行稳定分析。

当风电场并入非理想电网时，风机等效阻抗与电网线路阻抗产生谐振效应，并网点电压和电流的关系如下：

(20)

其中，Zg为dq坐标系下的电网阻抗矩阵，即：

式中，G为回率矩阵[15]，即电网等效阻抗与风机阻抗之比。系统稳定性取决于系统输出端口电压和电流的稳定性，因此若G满足Nyquist稳定判据，其Nyquist曲线不绕过点(-1,j0) 点时，该风机并网系统稳定，在稳定状态下，Nyquist曲线越接近(-1,j0)点，系统稳定裕度越大。

系统回率矩阵有两个特征值，其特征轨迹如图6所示。当参数改变时，外圆曲线永不包围(-1,j0)点，内圆曲线可能出现包围情况，为节省运行时间，提高计算效率，仅画出决定稳定性的特征轨迹，即方框中内圆黑色曲线。

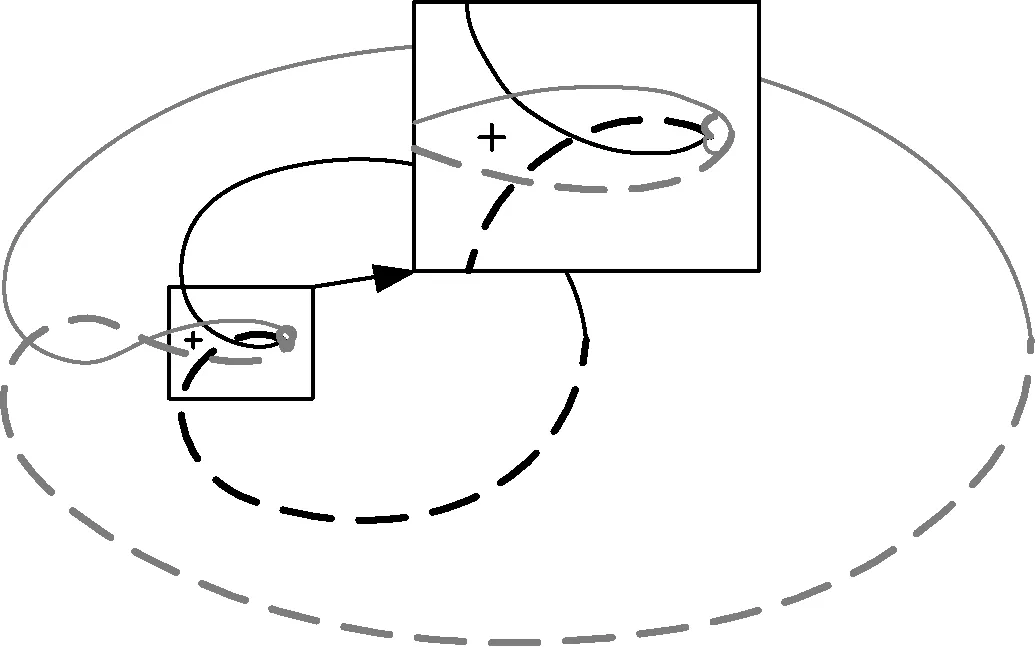
图6 Nyquist曲线示意图

为研究影响风机并网系统稳定性的可能因素，按照五个板块中的参数依次进行稳定性分析：转子侧内环、外环、PLL参数；网侧内环、外环、PLL参数；GSC出口滤波电容电感；直流母线电容；线路电感。设置合理的参数范围与步进系数，观察Nyquist曲线呈现靠近 (-1,j0)点的状态。

4.1 转子侧内环、外环、PLL控制参数

为研究RSC内外环以及PLL比例积分参数对系统稳定性的影响，改变其控制参数，系统广义奈奎斯特曲线如图7所示。图7(a)中设置内环比例参数从 0.6 pu变到1.2 pu，步进系数0.2 pu，当参数小于0.98 pu时，系统可能处于不稳定状态。

图7 RSC内外环以及PLL控制参数

而对于图7(b)中内环积分变化时稳定性无明显变化，说明该参数不是影响系统稳定性的主要因素。图7(c)中设置有功功率外环比例参数从0.5～2 pu的变化范围，当参数处于1.40～1.62 pu时，系统可能处于不稳定状态，但参数小于1.4 pu或大于1.62 pu时都趋于稳定状态。图7(d)中设置无功功率外环比例参数从1 pu变到2 pu，当参数小于1.15 pu时，系统可能处于不稳定状态。而外环积分参数与内环积分参数一样，对系统稳定性基本无影响。图7(e)中设置PLL比例参数从20 00 pu变到10 000 pu，当参数大于5 000 pu时，系统可能处于不稳定状态。图7(f)中设置积分参数从50 pu变到5 050 pu，随着参数增大，系统稳定裕度增加，但该参数对系统稳定性无决定性影响。

4.2 网侧内环、外环、PLL控制参数

为研究电GSC内外环以及PLL比例积分参数对系统稳定性的影响，采用与转子侧相同方法，系统广义奈奎斯特曲线如图8所示。图8(c)中设置直流电压外环比例参数从0.3 pu变到0.8 pu，当参数处于0.5～0.69 pu之间时，系统可能处于不稳定状态，但参数小于0.5 pu或大于0.69 pu时都趋于稳定状态。从图8可以看出GSC内环比例积分参数、外环积分参数、相环比例积分参数都不是影响系统稳定性的主要因素。

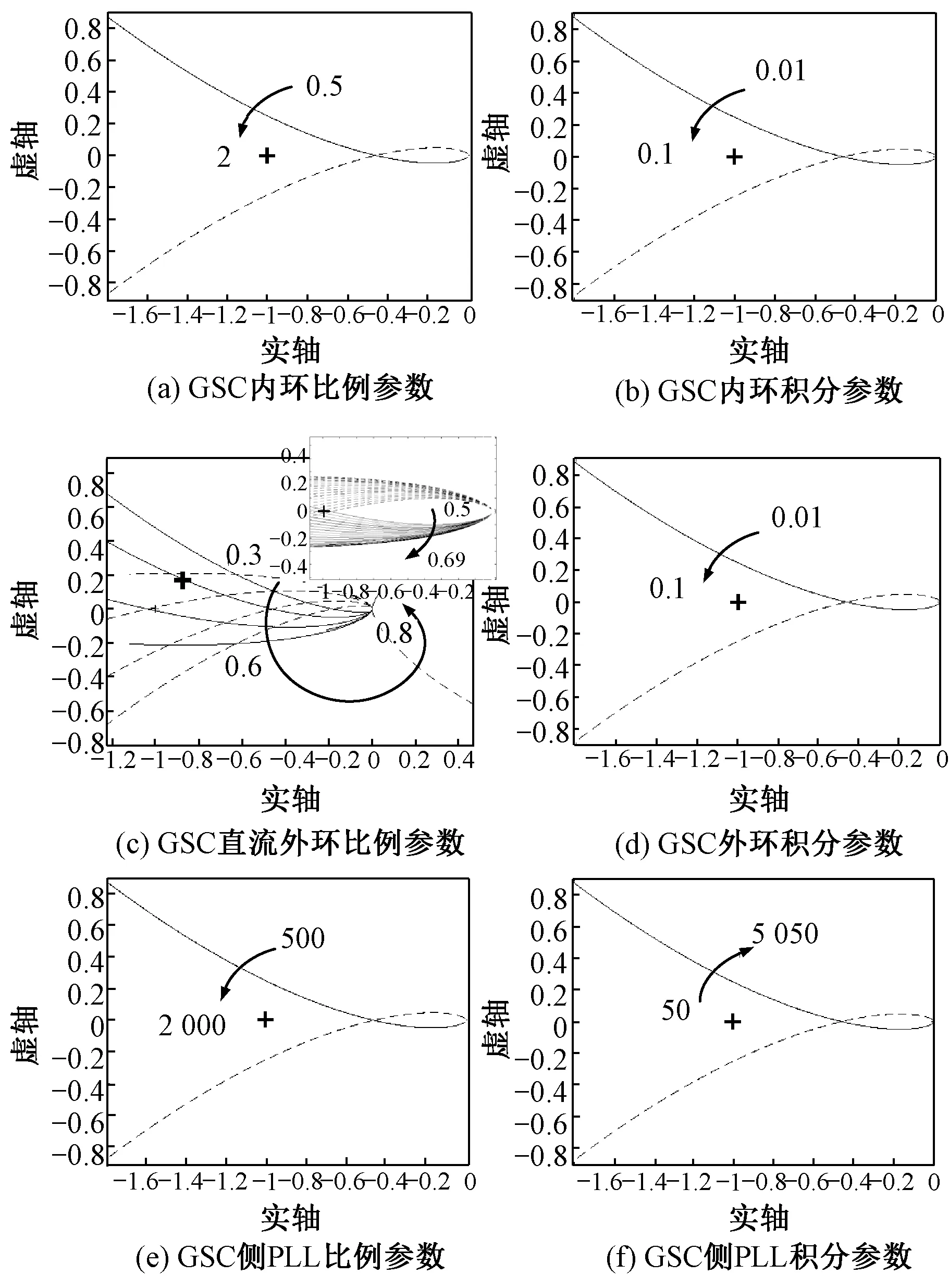
图8 GSC内外环以及PLL控制参数

4.3 GSC出口滤波器参数

改变GSC出口滤波电容电感，系统广义奈奎斯特曲线如图9所示。图9(a)中设置电容参数从1 pu变到10 pu，系统稳定裕度增加，系统稳定性无明显变化。由图9(b)可见滤波电感参数不是影响系统稳定性的主要因素。

4.4 直流母线电容和线路串抗

改变直流母线电容以及线路电感，系统广义奈奎斯特曲线如图10所示。

图10(a)中设置直流母线电容从2.5 pu变到4.5 pu，当线路电感小于3.54 pu时，Nyquist曲线包围(-1,j0)点，系统处于不稳定状态。当线路电阻不变时，串抗可以代表短路比，图10(a)中设置线路电感从0.5 pu变到2 pu，当线路电感大于1.09 pu时，Nyquist曲线包围(-1,j0)点，系统处于不稳定状态，说明短路比越小，系统越不稳定。

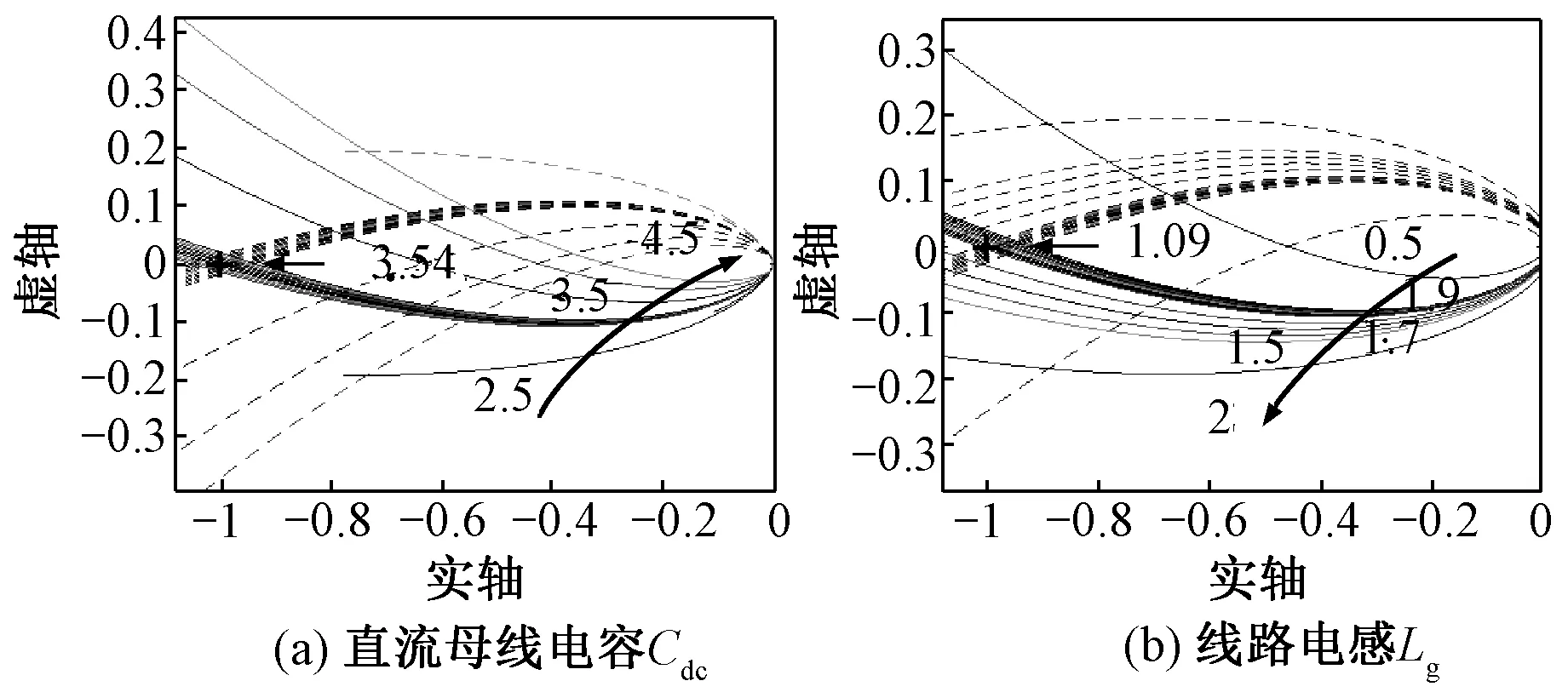
图10 直流母线电容与线路串抗参数

综上，DFIG所有参数中RSC内外环以及PLL比例参数、电网侧直流外环比例参数、直流母线电容以及系统短路比是影响其并网稳定性的重要因素，当各参数在以下范围取值时，系统可能不稳定运行：

(1)RSC内环比例参数设置小于0.98 pu时；

(2)RSC有功功率外环比例参数处于1.40～1.62 pu之间；

(3)RSC侧锁相环比例参数大于5 000 pu时；

(4)GSC直流电压外环比例参数设置大于0.7 pu时；

(5)直流母线电容设置小于3.54 pu时；

(6)线路电感设置大于1.09 pu时。

参数中对系统稳定性有影响但影响较小的有：RSC侧锁相环积分参数、GSC出口滤波电容参数。这些参数的改变会使系统稳定裕度增加，但对系统稳定性无明显影响，当系统接近临界稳定状态时，改变上述两种参数可能使系统变成不稳定状态。

5 仿真验证

利用在PSCAD/EMTDC中建立的麻黄山第四风电场的仿真模型，与第2节中PSCAD风电场并网模型一致，线路参数以及控制参数均根据实际正常运行的风机参数进行设计，如表1所示。改变RSC内环控制参数、RSC有功功率外环控制参数以及GSC直流电压外环控制参数，进行仿真验证，仿真结果如图11所示。

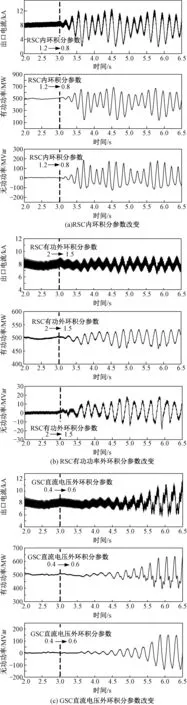
图11 风电场出口电流、有功功率与无功功率

在风电场正常运行3 s后，根据第3节中所计算的能够引起风电场振荡的控制参数范围，分别改变风机RSC内环控制参数1.2 pu为0.8 pu，风机RSC有功功率外环参数2 pu为1.5 pu，风机GSC直流电压外环参数0.4 pu为0.6 pu，经过改变控制参数的风电场出口电流、有功功率与无功功率分别对应图11(a)、图11(b)、图11(c)，不难看出风电场从3s后开始振荡，说明在不稳定参数范围内改变控制参数，风电场稳定性确实会受到影响。其中，图11(a)中改变RSC内环积分参数时，电流与功率振荡幅度较大，振荡发生于改变控制参数瞬间；图11(b)中改变RSC有功功率外环积分参数时，电流与功率振荡幅度较小；图11(c)中改变GSC直流电压外环参数时，振荡在控制参数改变之后才发生，说明GSC侧控制效果经直流环节传递到RSC侧，两侧换流器相互作用引发振荡。

6 结论

本文在dq坐标系下建立了DFIG阻抗模型，考虑了RSC与GSC的内环、外环、PLL，以及两个换流器之间传递波动的直流环节对阻抗模型的影响，画出了完整的阻抗模型在dq坐标系下的阻频特性以及忽略PLL、外环以及直流环节的模型的阻频特性，经对比，考虑这些环节对建立准确的DFIG中低频阻抗是必要的。

针对MIMO系统，利用广义奈奎斯特稳定判据对该风机并网系统进行稳定性分析，利用PSCAD中仿真数据，设置合理参数改变范围，在Matlab中画出不同参数下系统Nyquist曲线，由此可直观得到DFIG并网系统稳定性与RSC内环、外环与PLL比例参数和直流环节关系较为密切，与系统短路比也有关的结论。利用宁夏电网麻黄山双馈风电场参数建立仿真算例，仿真验证结论的正确性。

建立准确的风机阻抗模型，为准确分析系统参数影响风电场稳定性提供有利支持，同时了解到系统参数对稳定性的不同影响程度，为后续化简用于分析风电场并网稳定性的阻抗模型提供一定依据，在不影响分析准确性的前提下，最大程度化简阻抗模型。

致谢：本文得到宁夏电科院《宁夏电网多换流器次同步振荡机理分析与防范措施研究》科技项目的资助，谨此致谢。