正弦与非正弦激励下高频变压器磁心损耗计算与验证

刘福贵， 赵 琳， 蒋嘉诚

(1. 省部共建电工装备可靠性与智能化国家重点实验室， 河北工业大学， 天津 300130；2. 河北省电磁场与电器可靠性重点实验室， 河北工业大学， 天津 300130)

1 引言

近年来，随着电力电子技术的快速发展，电力电子变压器广泛应用在电网中。国内外学者为设计出更加高效，更易控制的电力电子变压器不断地进行探索[1，2]。随着电力电子变压器的持续发展，在其中起到电气隔离与电压等级变换的高频变压器的应用越来越广泛。由于工作频率的提升，高频变压器磁心的损耗相应增高，导致磁心内部温度增高，降低了高频变压器的使用寿命以及系统的稳定性，因此研究高频变压器的磁心损耗具有重要意义[3-5]。

目前，磁心损耗主要计算方法分为两类，一类为磁滞模型法，另一类为损耗数学模型法。磁滞模型虽然具有明确的物理含义且精度较高，但模型过于复杂，参数提取困难，耗费时间较长，所以一般在工程实践中常采用损耗数学模型法来进行计算[6]。文献[7]将损耗分离模型由三项式变为两项式，在此基础上将激励电压傅里叶分解成多次谐波叠加形式，引入激励电压的平均值与有效值，提取校正系数进而求得磁心损耗。但由于文中将剩余损耗项归于涡流损耗，影响了损耗计算的准确性。文献[8]将动态磁滞回线与椭圆磁滞回线进行等效，求得等效磁场强度、磁通密度与频率之间的关系，进而求得磁心损耗。但文中缺少对方波与三角波电压激励下的损耗计算分析。文献[9]对比分析了三种基于损耗分离理论下的非正弦计算模型，将三种模型在PWM激励下的计算结果与实验数据进行比较，发现三种模型在磁通密度大于1 T的情况下三种模型计算结果精确。但在磁通密度较小时，计算误差较大。

为解决上述所存在的问题，实现高频变压器磁心损耗的准确计算，本文基于Bertotti损耗分离模型，引入了涡流损耗与剩余损耗修正系数，推导出在方波和三角波激励下损耗分离计算模型，实现了在非正弦激励下高频变压器磁心损耗的计算。并根据损耗系数变化特征，将损耗系数改进，提高了正弦激励下模型的计算精度。在此基础上代入修正系数，对非正弦激励下损耗分离模型进一步改进，并将测量值与计算结果进行比较，验证了文中所提模型的有效性。

2 非正弦激励下损耗分离模型

意大利学者Bertotti解析了铁磁材料损耗产生的不同机理，将铁磁材料的损耗分为三部分：磁滞损耗Ph、涡流损耗Pe、剩余损耗Pex[10]。

2.1 经典正弦损耗分离模型

根据Bertotti损耗分离理论，损耗模型的计算公式如式(1)所示：

(1)

式中，f为激励电压频率，Hz；Bm为磁通密度峰值，T；σ为材料电导率；ρ为材料密度；d为材料叠片厚度,mm；T为磁化周期,s；G为无量纲系数(G=0.137 5)；S为叠片横截面积，mm2；V0为铁磁材料内部统计参数。

在正弦电压激励条件下，磁通密度表达式为B(t)=Bmcos(ωt)，代入式(1)可得正弦激励下损耗计算公式为：

(2)

式中，Kh为磁滞损耗系数；Ke为涡流损耗系数；Kex为剩余损耗系数。

2.2 确定正弦损耗分离模型参数

为了得到正弦电压激励下Bertotti损耗分离模型损耗系数，本文首先采用环形测量法测量非晶与纳米晶磁心损耗数据。在正弦激励下,测量频率范围为1～10 kHz(每1 kHz递增)，测量非晶磁环磁通密度范围为0.1～1.3 T(每0.1 T递增)，测量纳米晶材料磁通密度范围为0.1～1.2 T(每0.1 T递增)，得到正弦激励下非晶和纳米晶材料不同工况下损耗数据如表1和表2所示。

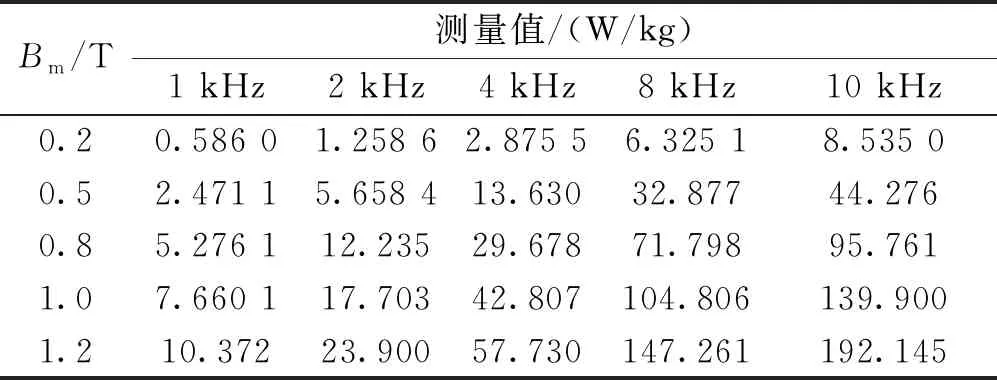
表1 非晶正弦激励下损耗数据

然后，依照测量得到的损耗数据，采用最小二乘法对式(2)进行损耗参数拟合，得到正弦电压激励下非晶与纳米晶磁心损耗计算公式为：

(3)

(4)

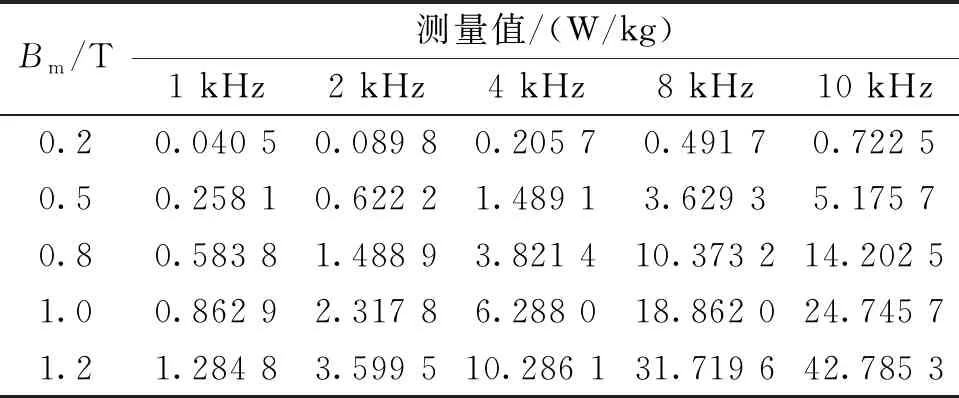
表2 纳米晶正弦激励下损耗数据

2.3 修正损耗分离模型

在实际应用中，高频变压器常工作于方波与三角波等非正弦电压的激励下，因此，式(2)不能满足计算精度的要求。参照损耗分离理论中各个损耗产生的机理，在磁感应强度与频率相同的情况下，磁滞损耗一般不发生变化。所以，在不同电压波形的激励下，磁心损耗的差异主要由于涡流以及剩余损耗发生变化。因此，为得到方波和三角波电压激励下磁心损耗分离计算模型，本文引入涡流与剩余损耗修正系数，对经典正弦损耗分离模型进行修正[11，12]。

2.3.1 方波激励下损耗分离模型

方波激励时电压与磁通密度在一个周期内随时间变化波形如图1所示，公式如式(5)和式(6)所示。

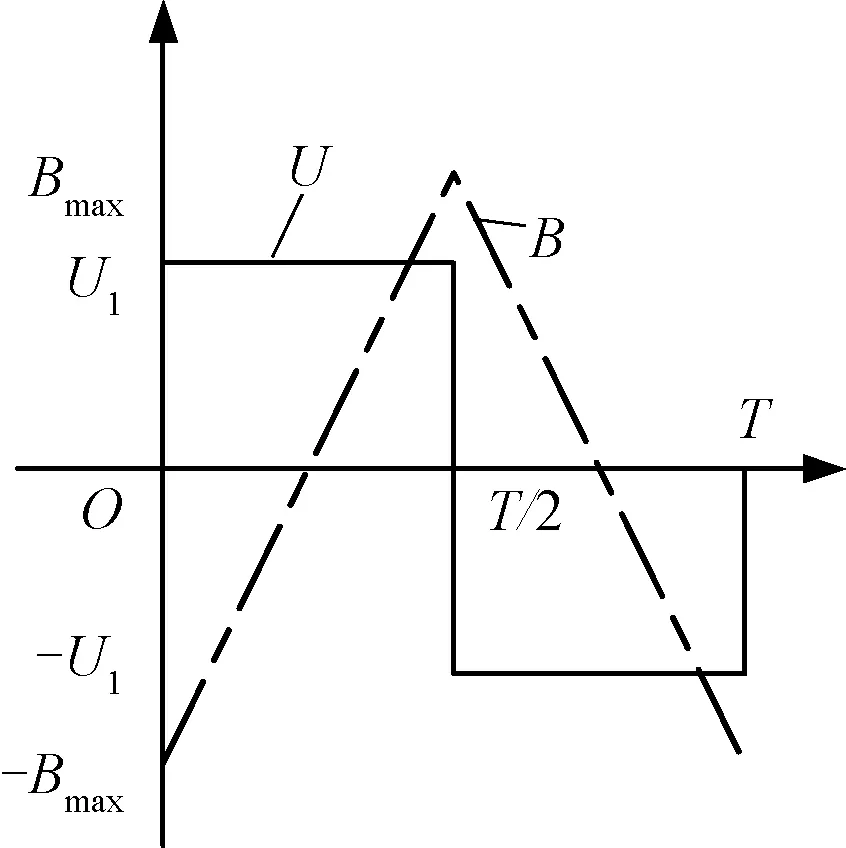
图1 方波电压及磁通密度波形

(5)

(6)

由式(6)可得出方波电压激励下磁通密度变化率，将所得公式代入式(1)，可得方波激励下涡流和剩余损耗计算公式为：

(7)

(8)

将式(7)与正弦激励下的涡流损耗计算公式相除，可得方波电压激励下涡流损耗修正系数为：

(9)

同理，方波激励下剩余损耗修正系数为：

(10)

2.3.2 三角波激励下损耗模型计算方法

三角波激励时电压与磁通密度在一个周期内随时间变化波形如图2所示，公式如式(11)和式(12)所示。

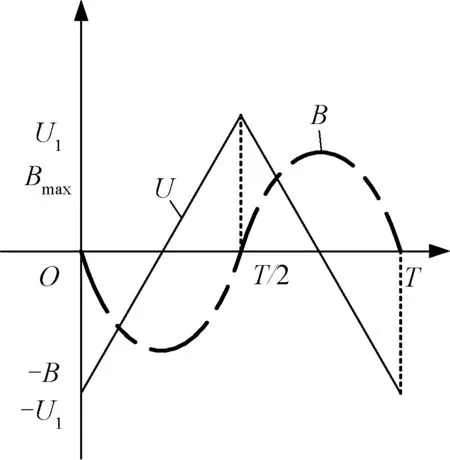
图2 三角波电压及磁通密度波形

(11)

(12)

由式(12)可得出三角波电压激励下磁通密度变化率，将所得公式代入式(1)，可得三角波电压激励下涡流和剩余损耗计算公式为：

(13)

(14)

将式(13)与正弦激励下的涡流损耗计算公式相除，可得三角波电压激励下涡流损耗修正系数为：

(15)

同理可得三角波激励下剩余损耗修正系数为：

(16)

引入涡流与剩余损耗修正系数，可以由正弦计算公式推导出非正弦激励下损耗计算公式，公式如式(17)所示，表3为方波和三角波激励下损耗修正系数。

(17)

表3 方波和三角波激励下损耗模型修正系数

由表3可以观察到，方波的涡流、剩余损耗修正系数均小于1，三角波涡流、剩余损耗系数均大于1，因此，可以推断出在给定相同工作频率与相同磁密峰值的条件下，三角波电压激励下的损耗数值最大，方波电压激励下的损耗数值最小。

3 磁性测量与分析

为了验证第2节所提修正系数的有效性，对比分析非晶和纳米晶材料的磁特性，得到不同工况下磁心的损耗数据，本文采用环形测量法，测量在正弦和非正弦激励下磁心的损耗特性与磁特性，样品为安泰公司生产的环形非晶与纳米晶磁心。磁心原副边线圈采用多股铜线并绕方式，以减少线圈内的趋肤效应。环形非晶磁心尺寸为外径50 mm，内径40 mm，高度为20 mm，带材厚度为0.025 mm。环形纳米晶磁心尺寸为外径50 mm，内径40 mm，高度为25 mm，带材厚度为0.02 mm。

3.1 磁通密度控制方法

在实验室搭建磁特性测试系统，测量正弦、方波及三角波在频率范围为1～10 kHz，不同磁通密度下的损耗值。实验在空载条件下进行，测量系统由ARB波形编辑软件、信号发生器WF1974、功率放大器NF4520、示波器、功率分析仪与非晶纳米晶磁心组成。通过ARB波形编辑软件编辑生成非正弦波，将所生成的非正弦波形信号传递给信号发生器。调节信号发生器可调节所施加激励电压与频率的大小，将给定信息传递给功率放大器，功率放大器再将给定激励施加给所试验样品。同时，功率分析仪记录损耗数据，示波器记录一次侧电流与二次侧感应电压的波形，测量系统如图3所示[13，14]。

图3 磁特性测量系统

由法拉第电磁感应定律原理可求得感应电压与磁通密度关系，关系如式(18)所示：

(18)

式中，u(t)为感应电压，V；N为绕组匝数；S为磁心截面积，mm2。

将式(6)和式(12)进行求导并代入式(18),可推出在方波和三角波电压激励下，二次侧感应电压与磁通密度之间的关系如下所示。

方波电压激励下：

(19)

三角波电压激励下：

(20)

磁心一次侧绕组所施加的激励电压控制磁心内部的激磁电流，激磁电流的改变引起激磁磁场发生变化。而激磁磁场的改变导致了磁心内磁通密度变化，由法拉第电磁感应定律可知，测量二次侧感应电压可以相应地测出磁心内部磁通密度，因此，在实际测量过程中，调节激励电压可以相应地控制磁心内部的磁通密度。

将二次侧感应电压进行积分，可得出在相应的感应电压情况下磁心内磁通密度波形，波形如图4所示。

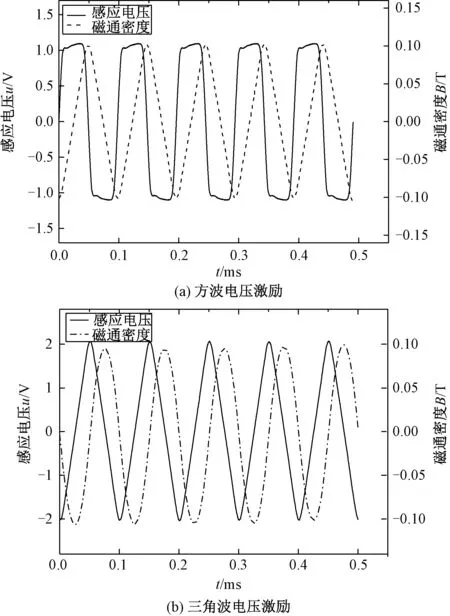
图4 不同激励下感应电压与磁通密度波形

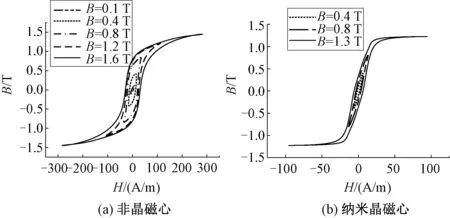
图5 f=4 kHz时，不同磁通下非晶与纳米晶磁滞回线

根据示波器保存的一次侧电流与二次侧感应电压波形，处理波形数据可得，非晶和纳米晶磁心在频率为4 kHz，不同磁通密度时的磁滞回线如图5所示。由图5可知，纳米晶磁心的矫顽力与磁滞回线面积小于非晶磁心，因此可以得出在相同工况下纳米晶材料产生的损耗远小于非晶材料，性能优越。但由于纳米晶材料不易制取，价格昂贵，所以设计高频变压器时，应根据所需工况要求选择材料类型。

3.2 对比分析

依据测量所得到的实验数据，得到非晶磁心在正弦、方波与三角波电压激励下的损耗P与频率变化关系如图6所示。

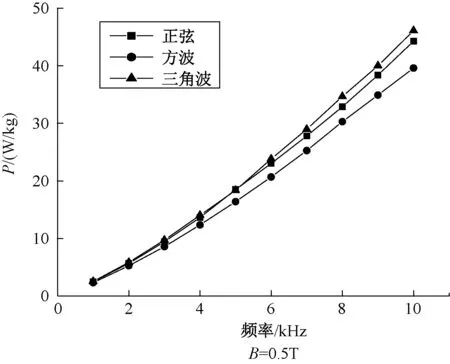
图6 Bm=0.5 T时非晶磁心损耗与频率关系

由图6可以观察到，磁心损耗大小与激励电压波形密切相关，在不同激励下损耗数值不同。三角波电压激励下损耗数值最大，方波电压激励下损耗数值最小，验证了上文所提出修正损耗系数的有效性。

4 损耗分离计算模型的改进

4.1 分离损耗

能准确地分离出磁滞损耗、涡流损耗和剩余损耗，是提取磁心损耗系数过程中的重要一步，本文采取如下步骤分离损耗。

(1)将式(2)左右两边同时除以频率f，可以得到损耗W计算公式为：

(21)

(2)涡流损耗公式有明确的物理推导，所以，可以用涡流损耗公式来准确地计算磁心内的涡流损耗，因此将式(21)左边减去涡流损耗计算值，得到磁滞损耗加剩余损耗的和如下所示：

(22)

由上述分离过程可以发现总损耗减去涡流耗后，损耗计算模型变为了与频率的1/2次方有关的函数。基于W-f1/2函数的图像特点，图像的截距为H，图斜率为L。因而，可以得到，磁滞损耗大小为H，剩余损耗大小为Lf1/2。经过数据处理与数据拟合可得到不同工况下的H与L，进而得到Kh与Kex的值。

4.2 损耗分离计算模型的改进

在进行上述分离损耗过程中发现，在不同工况下得到的损耗系数Kh与Kex不是固定值，会随着磁通密度的改变而改变，考虑到高频变压器设计时所需精度的要求，在经典正弦模型的基础上提出一种改进的损耗分离模型，计算公式如下所示：

(23)

式中，Kh(Bm)为磁滞损耗系数，Kh(Bm)=C0+C1Bm+C2Bm2+C3Bm3；Kex(Bm)为剩余损耗系数，Kex(Bm)=D0+D1Bm+D2Bm2+D3Bm3。

在式(23)的基础上，分别代入第2节所推导三角波与方波修正系数，可得出方波与三角波激励下损耗计算公式如下所示。

方波激励下损耗计算公式为：

(24)

三角波激励下损耗计算公式为：

(25)

式中，ξ1为方波激励下涡流损耗修正系数；η1为方波激励下剩余损耗系数；ξ2为三角波激励下涡流损耗修正系数；η2为三角波激励下剩余损耗系数。

在正弦激励条件下非晶与纳米晶的损耗系数Kh(Bm)和Kex(Bm)与磁通密度的关系如图7和图8所示，图中非晶拟合的相关系数的值分别为0.984 5与0.989 1，纳米晶拟合的相关系数的值分别为0.983 1与0.997 6，展现出了良好的相关性。

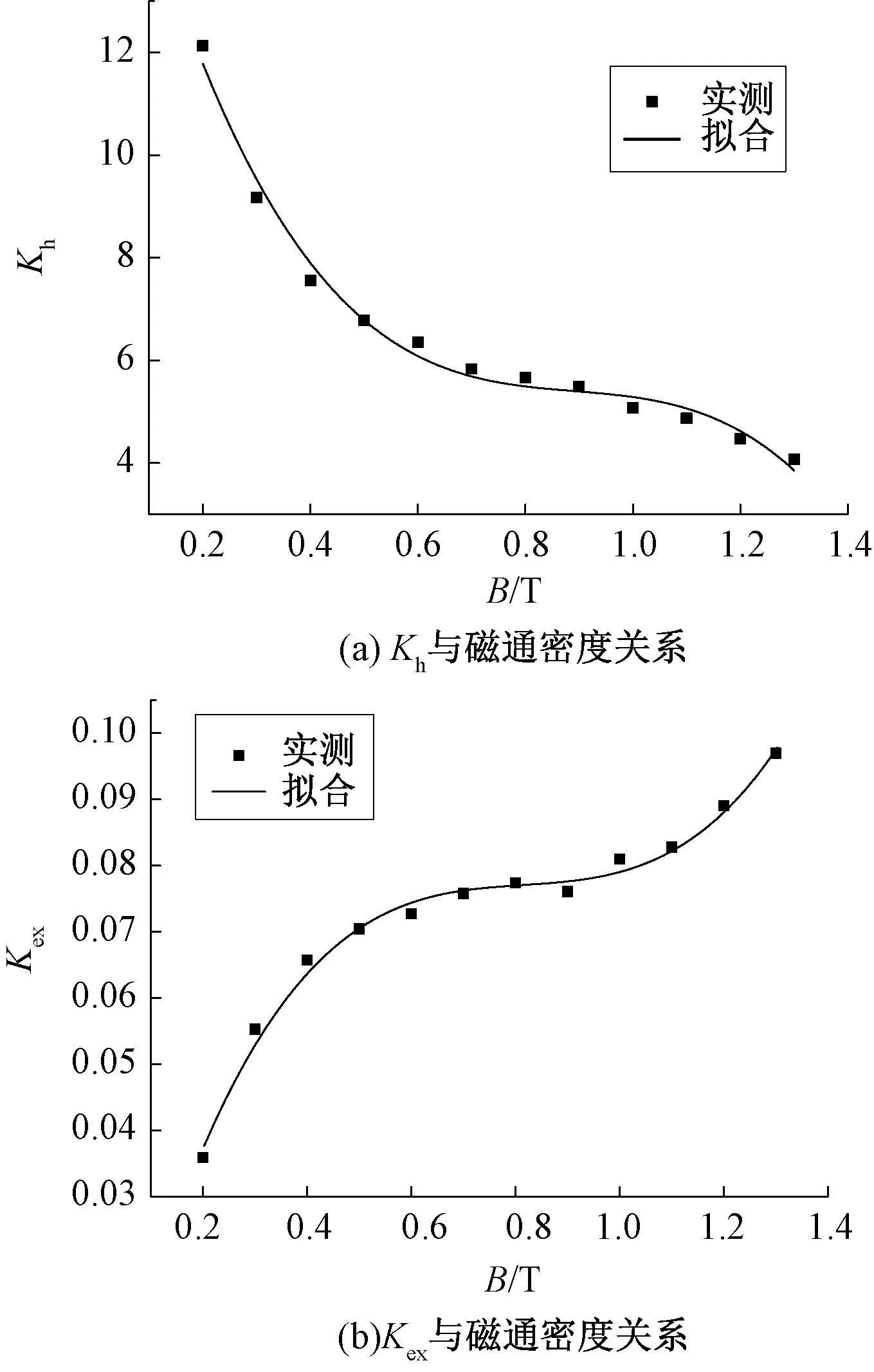
图7 非晶磁心损耗系数与磁通密度关系

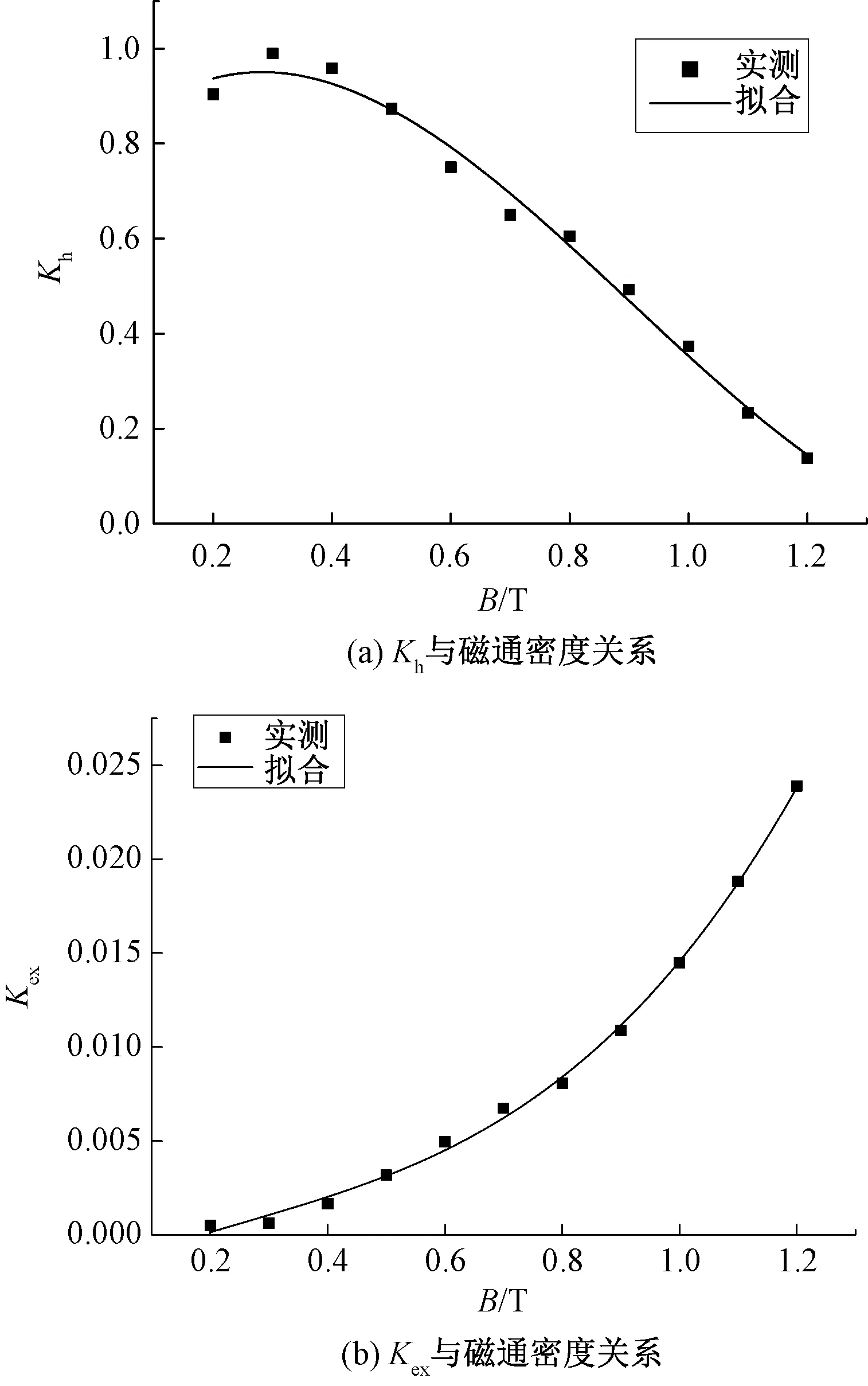
图8 纳米晶磁心损耗系数与磁通密度关系

因此，得到Kh(Bm)与Kex(Bm)公式中参数值大小如表4与表5所示。

表4 Kh(Bm)中的参数值

表5 Kex(Bm)中的参数值

4.3 改进损耗模型的验证

为了检验本文所提出改进损耗分离计算模型的准确性，将改进模型的计算值与实验值进行比较，误差大小如表6所示。并将经典正弦损耗模型与改进正弦损耗模型的计算精度进行对比，结果如表7所示。

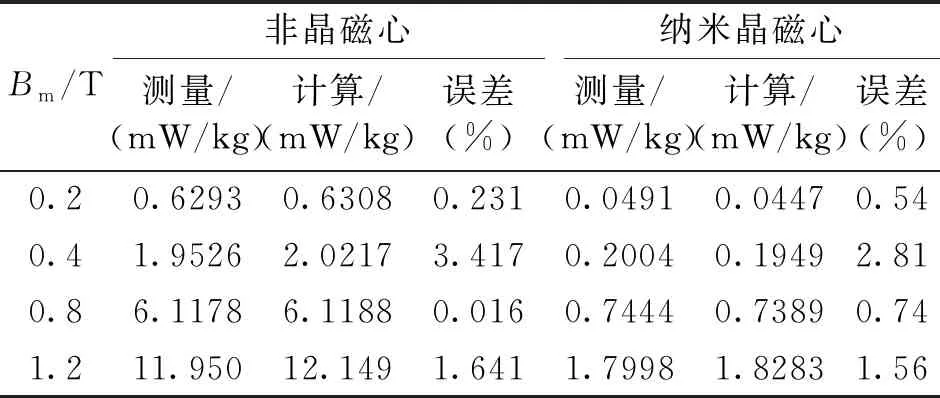
表6 改进损耗模型计算误差

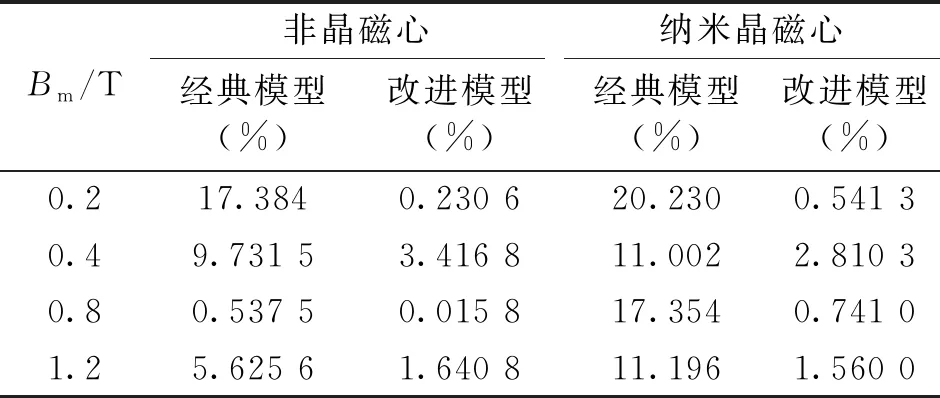
表7 经典损耗模型与改进损耗模型误差对比

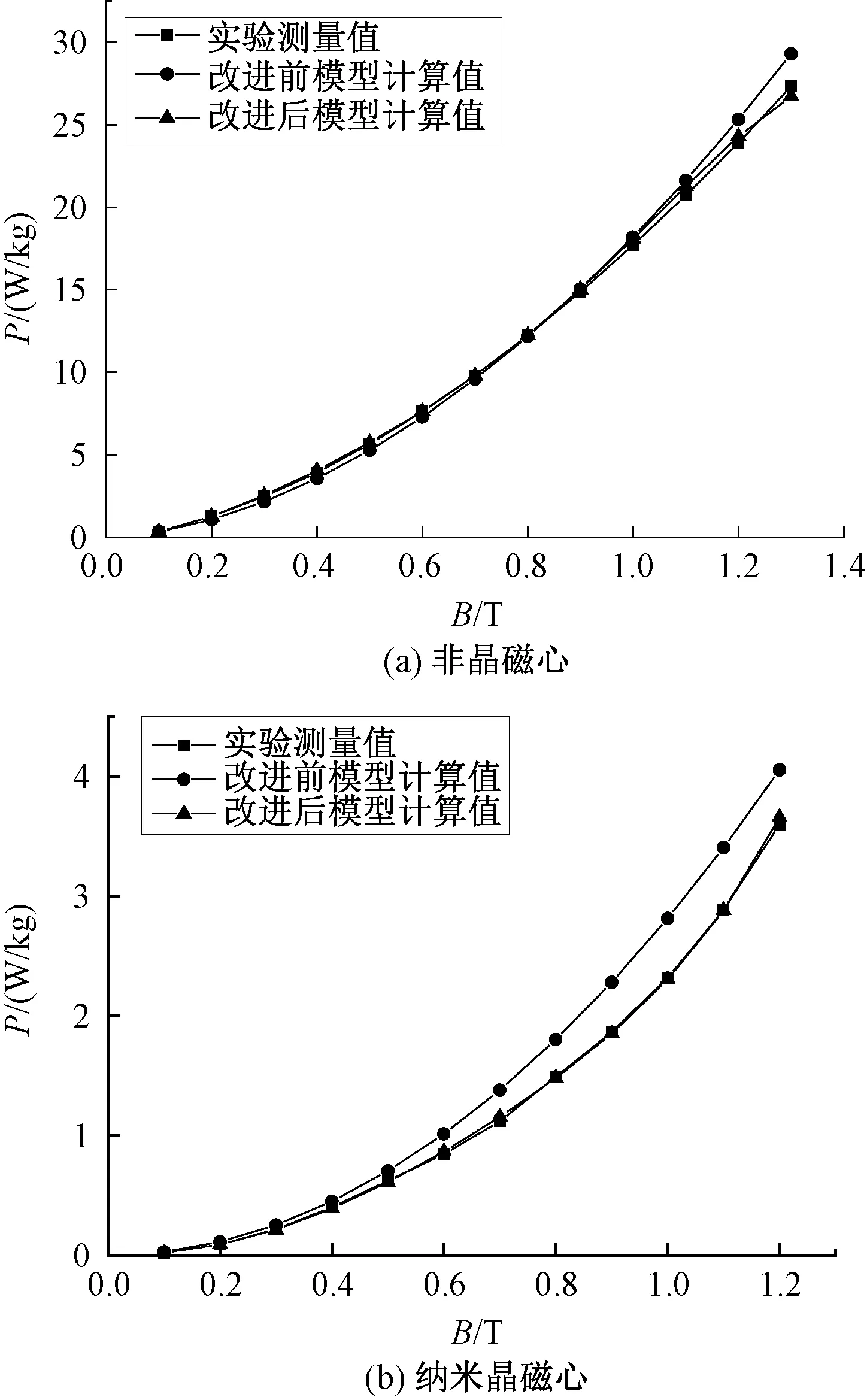
图9 改进前与改进后模型损耗对比

由表7和图9可知，在正弦电压的激励下，改进损耗分离模型的计算结果与经典损耗分离模型的计算结果相比与实验数据吻合度更高，非晶与纳米晶磁心的计算误差均在8%以内，满足精度要求。

非晶与纳米晶磁心在方波和三角波激励下的损耗可依照式(24)和式(25)进行计算，得到改进后非正弦损耗分离模型的计算结果与实验数据对比如图10所示。

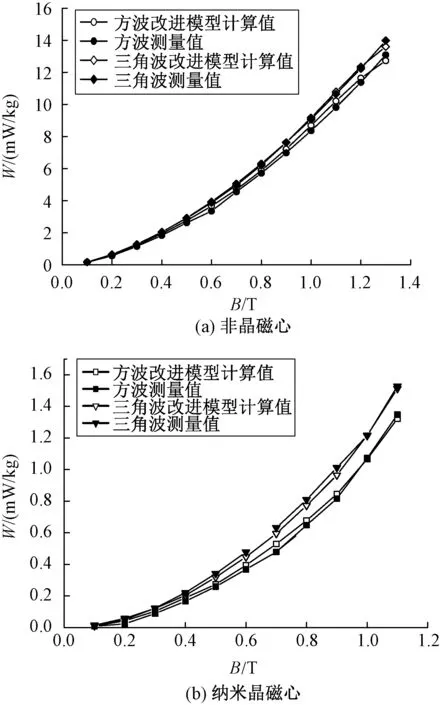
图10 f=2 kHz时改进后损耗模型计算值与测量值对比

由图10可知，在方波与三角波电压激励下，非晶磁心与纳米晶磁心改进后模型的计算结果与实验数据误差较小，契合度较高，验证了文中所提出的改进损耗分离模型在非正弦电压激励下的有效性与准确性。

5 结论

本文在经典正弦损耗分离模型的基础上，根据磁通波形特征推导出涡流损耗与剩余损耗修正系数，进而得到非正弦激励下修正损耗分离计算模型。并依据损耗系数特征，提出一种改进损耗分离计算模型方法，提升了模型计算精度，并分别带入损耗修正系数，得到非正弦激励下改进的损耗模型，将改进后模型计算值与实验值进行对比，发现模型有较好的契合度，检验了所提模型的可行性与有效性，对于精确计算高频变压器磁心损耗具有一定参考价值。