计及系统级控制的柔性直流牵引供电系统潮流计算方法

席嫣娜， 王方敏， 李占赫， 李笑倩， 魏应冬， 宋宝同， 李 伟， 沈卓轩

(1. 国网北京市电力公司， 北京 100031； 2. 电力系统及发电设备控制和仿真国家重点实验室, 清华大学电机系, 北京 100084； 3. 北京电力经济技术研究院有限公司， 北京 100055)

1 引言

随着城市轨道交通的快速发展，其对供电系统的容量和供电质量提出了更高的要求。随着电力电子技术的发展及其在电力系统中的应用，机车过分相、电能质量等长期在牵引供电系统(Traction Power Supply System, TPSS)中存在的难题得到了很多解决方案[1-4]。其中，基于电压源型换流器(Voltage Sourced Converter，VSC)的柔性直流牵引供电系统(VSC-TPSS)，具有灵活控制直流电压的能力，能够克服常规二极管整流方案[5]和逆变回馈方案[6]在牵引供电时直流电压不可控、电压偏差大等问题，具有降低牵引所峰值容量、减小接触网电压偏差、提高机车再生制动能量利用率等诸多优势，具有广阔的应用前景。

潮流计算能够根据机车运行情况，计算TPSS节点电压和功率分布，是TPSS分析和设计的基础，是确定牵引所容量、外电源接入方式等关键问题的重要依据。文献[7]基于高斯迭代法，主要针对二极管整流方案研究了计及单向导通特性的牵引所的直流潮流算法。文献[8]主要针对逆变回馈方案研究了基于牛顿迭代法的直流潮流算法，提出了电压下垂控制的直流潮流算法。文献[9]基于高斯迭代法，研究了包含储能装置、过压保护、单相导通与非单相导通牵引所等各种模型的直流TPSS潮流算法。上述文献提出的算法可以高效地对现有TPSS进行稳态分析，但是其主要考虑的供电方案与柔直方案的潮流特性不同，不能直接适用于VSC-TPSS潮流计算。如何在潮流计算中模拟复杂的系统级控制方式仍有待进一步的研究。

与二极管整流方案和逆变回馈方案不同，VSC-TPSS的潮流特性主要由系统级控制确定。现有的VSC-TPSS系统级控制方法主要包括主从控制、裕度控制和下垂控制[10]。其中，考虑到电力机车是单相冲击性负荷，接触网电压波动范围大等因素，下垂控制是系统级控制的重要策略。由于常规下垂控制具有电压偏差大、均流效果不足等缺陷，国内外学者提出了改进下垂控制策略。文献[11]在变流器采用下垂控制的基础上，加入高层级的能量管理系统以调节下垂曲线的截距，使得接触网上的电压值更接近额定电压。文献[12]引入PI控制动态平移下垂曲线，使接触网上的电压更接近额定值。文献[13]同时调整下垂曲线的截距和斜率，在降低系统电压偏移的基础上，增加变流器之间的均流效果。采用不同的系统级控制策略，会导致系统潮流发生重大变化，因此VSC-TPSS的潮流计算需要准确地体现系统级控制的影响。因此，本文提出一种计及复杂系统级控制方式的VSC-TPSS潮流算法。

2 VSC-TPSS潮流模型建立方法

TPSS由110 kV或220 kV输电网供电，在集中供电方式下，由35 kV中压配电网向牵引所供电；在分散供电方式下，由10 kV中压配电网向牵引所供电。在牵引所内部设有变压器和基于全控器件的AC/DC双向变流器。中压交流电经变流器整流为750 V或者1 500 V直流电，向电力机车供能。在机车刹车制动时，机车的再生回馈制动能量以电能的形式向接触网反送，一部分能量被附近正处于牵引状态的机车消纳，一部分能量经过变流器逆变到交流电网。VSC-TPSS示意图如图1所示。

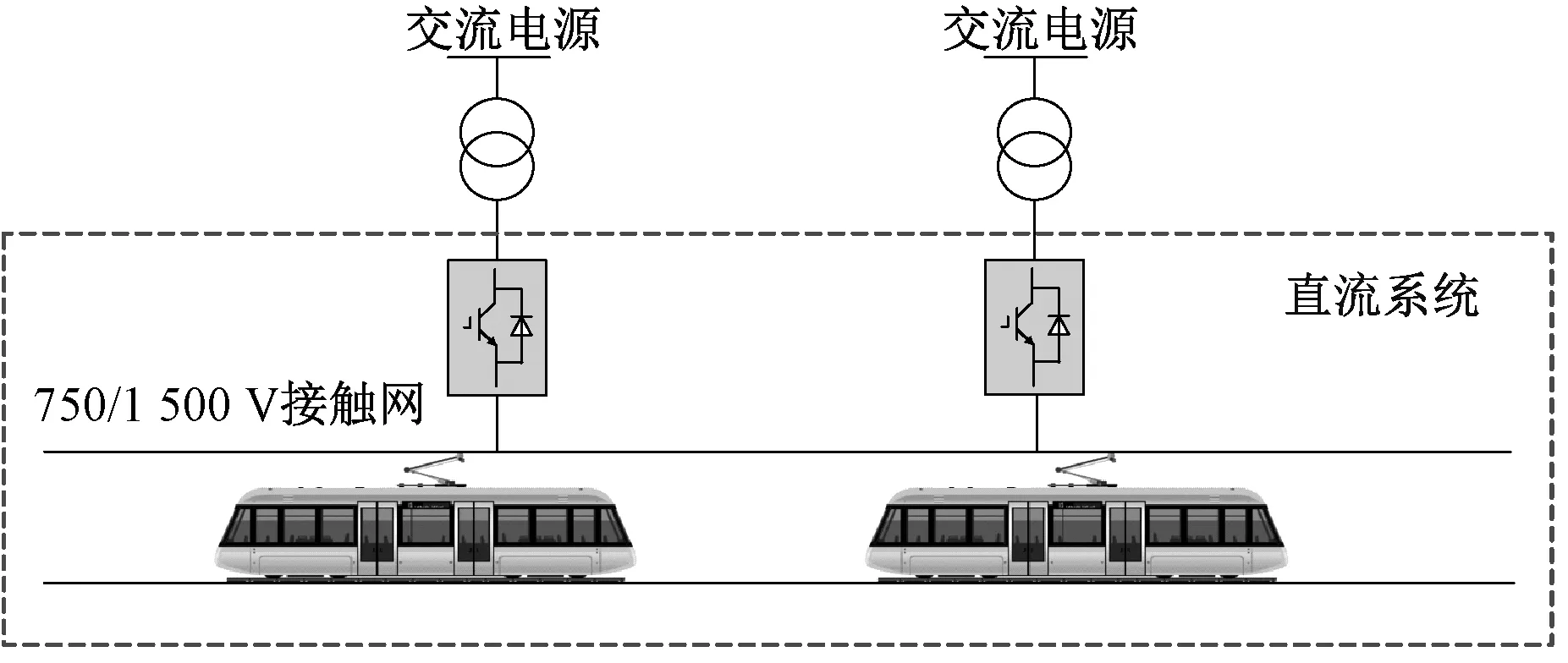
图1 VSC-TPSS示意图

2.1 系统级控制的建模方法

系统级控制建模是牵引所建模的前提和基础。由于变流器控制速度非常快，在潮流计算时，可认为变流器输出电压近似等于系统级控制的参考值。下垂控制是一种广泛应用的系统级控制方式。因此，本文主要以下垂控制为例，说明潮流计算中系统级控制的建模方法。

根据常规下垂控制策略，变流器输出电压U可以表示为：

U=Un-k0I

(1)

式中，Un为电压设定值；k0为下垂特性的斜率；I为变流器输出电流。

需要注意的是，对于改进下垂控制策略，下垂曲线的截距和斜率往往均作为控制自由度进行动态调整[11,13,14]。因此，采用改进下垂控制策略时，变流器输出电压U如式(2)所示：

U=Un-k0(aur-x)I+ΔU

(2)

式中，x为常数；ΔU取值如式(3)所示：

(3)

式中，NTSS为牵引所的数量，其中TSS表示牵引所；Ui为第i个牵引所的节点电压。调整ΔU可以在机车运行过程中，动态地上下平移下垂曲线，使得全系统总体的电压偏移更小。

另外，对于第i个牵引所，式(2)指数函数中参数a和r为常数，参数ui的取值如式(4)所示：

(4)

式中，Ii为第i个牵引所的节点注入电流；参数β为常数。调整ui可在机车运行过程中，动态地调整下垂曲线的斜率，让牵引所自适应地参与协同控制，提高牵引所之间的均流效果，降低对交流电网的冲击。

2.2 牵引所的建模方法

牵引所的模型如图2所示。由于变流器具有电压源特性，根据第2.1节的系统级控制建模方法，第n个牵引所可以用TSSUn、TSSIn两个节点和连接阻抗Rd来表征。

图2 牵引所建模示意图

TSSU节点表征变流器内电势，其节点电压Ud为已知量。TSSI节点模拟牵引所在接触网侧的端口，起联络节点的作用，没有节点注入功率，因此其节点注入电流为0。牵引所内部TSSU节点和TSSI节点之间的连接阻抗Rd模拟下垂控制的作用。

设i表示1到NTSS之间的整数，UTSSU及其导纳矩阵YTSSU可分别由式(5)和式(6)确定：

UTSSU=[Ud1,…,Udi,…,UdNTSS]T

(5)

YTSSU=diag(Rd1-1,…,Rdi-1,…,RdNTSS-1)

(6)

在常规下垂控制中，UTSSU和YTSSU中的元素都为式(1)中的常数，可以表示为：

(7)

在改进下垂控制中，UTSSU和YTSSU中的元素，需要根据式(2)和潮流计算结果不断更新，可表示为：

(8)

2.3 机车的建模方法

TPSS的潮流计算中，通常采用基于列车运行图的方式。机车的电流或功率、位置、速度由列车运行图提前确定[15，16]。为了降低潮流计算迭代次数，本文将机车等效为电流源(而非功率源)，其中第m辆机车用电流节点Trainm表示。与常规的机车建模方法不同，本文对机车电流节点计算时还考虑到了系统级控制对牵引计算的影响。这是因为在地铁TPSS中，由于电压等级较低，机车中牵引电机的工作情况受接触网电压的影响较大，因此机车功率和机车电流不仅是机车速度的函数，还是接触网电压的函数。因此，本文提出的潮流计算与牵引计算嵌套，具体算法详见第2.5节。

2.4 VSC-TPSS系统潮流模型

VSC-TPSS系统的状态变量为节点电压向量U和节点注入电流向量I，系统网络拓扑由节点导纳矩阵Y描述：

(9)

式中，由于Train节点和TSSU节点之间没有电气连接，所以Y的分块矩阵中对应Train节点和TSSU节点的互导纳矩阵为0。节点注入电流向量I中，ITrain由牵引计算给出，在潮流计算中为已知量；由第2.2节可知ITSSI为零向量；ITSSU待求。节点电压向量U中，UTSSI和UTrain待求，分别为TSSI节点和Train节点的电压向量；UTSSU可由系统级控制方式确定，在潮流计算中为已知量。节点导纳矩阵Y可以通过Y=AyAT建立，其中，A为节点支路关联矩阵，y为支路导纳矩阵。

2.5 潮流计算算法

算法总体的流程图如图3所示。为了体现牵引计算和潮流计算的相互影响，设计了外环迭代和内环迭代的双层嵌套计算方法。外环迭代，即考虑牵引网电压波动，更新牵引计算的迭代过程；内环迭代，即潮流计算内部的迭代过程。

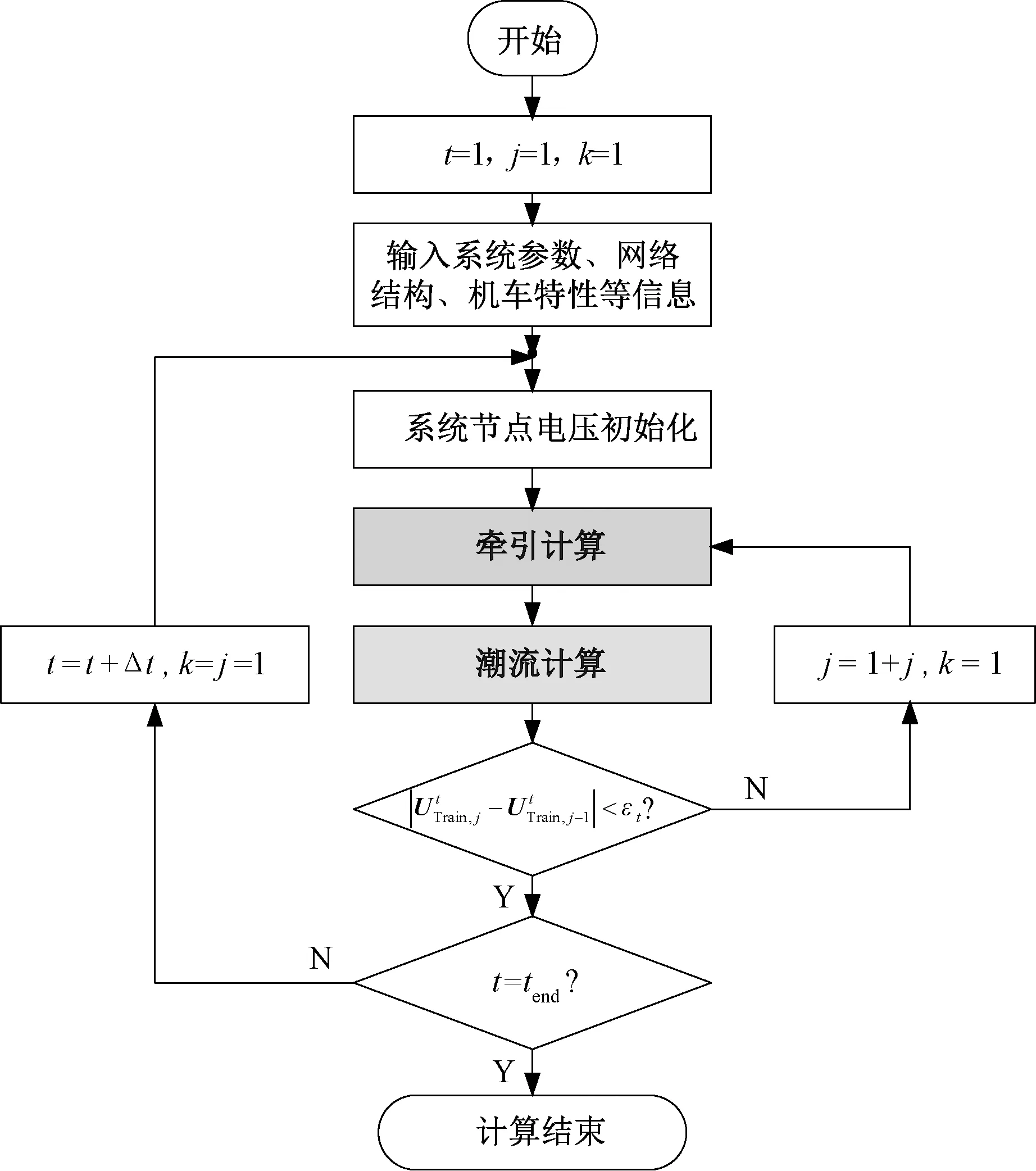
图3 算法总体流程图

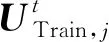
潮流计算的流程如图4所示，其中εp为潮流计算迭代中的最大允许误差。当系统级控制方式较为复杂时，需通过多次迭代的方式模拟控制作用下的潮流分布。迭代层数多后，可能有潮流不易收敛的情况出现。在这种情况下可引入阻尼因子α，在更新节点电压向量时用α阻尼节点电压的变化：

Uk=αUk+(1-α)Uk-1

(10)

式中，Uk和Uk-1分别为内环迭代次数为k和k-1时的节点电压向量。

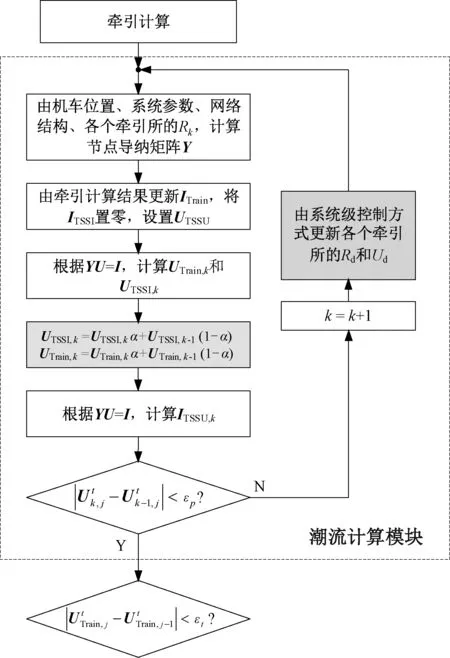
图4 潮流计算流程图

通过YU=I计算出Uk后，以阻尼因子α取0.5为例，通过式(10)可以把Uk调整为Uk和Uk-1的中点，减小节点电压向量更新的速度，避免节点电压向量更新过程中出现的反复循环而无法收敛的现象，从而帮助算法收敛。

3 实例分析

以北京地铁16号线路为例分析，该线路采用分散供电方式，由10 kV配电网供电。线路共有车站30个，其中有26个车站设置了牵引所，其余4个车站仅设置降压所。仅对TPSS部分进行计算，其示意图如图5所示。其中，牵引所1和牵引所26分别位于线路的两个端点，每个牵引所都从10 kV配电室中获得三相交流电，经整流后转化为额定值为1 500 V的直流电。在每个牵引所处，上下行线路并联。牵引所之间没有电分相，全线采用双边供电方式。

26座牵引所之间的距离如表1所示。表1中编号为1的区段，表示牵引所1到牵引所2之间的区段，以此类推，单行线上总共有25个区段。

潮流计算参数如表2所示，在该条件下以1 s为时间间隔，连续进行1 000个时间断面的潮流计算。绝大多数情况下阻尼因子α取0算法即可收敛；个别情况下节点电压的数值在更新过程中反复循环跳动，出现类似于“振荡”的现象，需要适当增大α阻尼节点电压的更新过程，帮助潮流收敛。

图5 北京地铁16号线路TPSS示意图

表1 牵引所间距

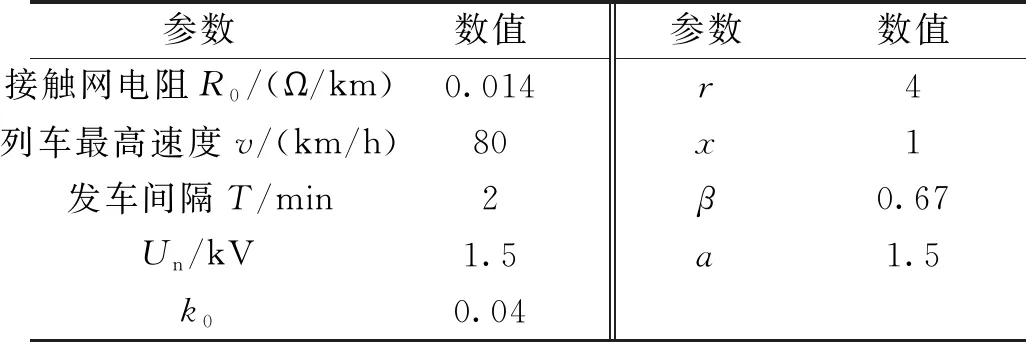
表2 潮流计算参数

当t=566 s，采用改进下垂控制策略时，牵引所1至牵引所3区域内各牵引所和车辆的潮流计算结果如图6所示。

图6中x轴所示为该时刻下相邻且按顺序排列的部分节点。机车1处于制动状态，反送的功率较大；机车5处于牵引状态，消耗的功率较大；其余机车处于惰行状态。牵引所1将机车1的功率反送到交流系统中，牵引所2和3向附近的机车供能。

得出1 000个时间断面内，75辆机车的输出电压的统计分布直方图如图7所示。根据图7可知，改进下垂控制能够起到减小电压波动范围的作用，将接触网电压尽可能控制在额定值附近。统计26个牵引所的峰值功率，两种系统级控制方式下的峰值功率对比如图8所示。根据图8可知，改进下垂控制可以显著提升系统的均流效果，降低牵引所的峰值功率，从而降低建设成本，减小对电网的冲击。

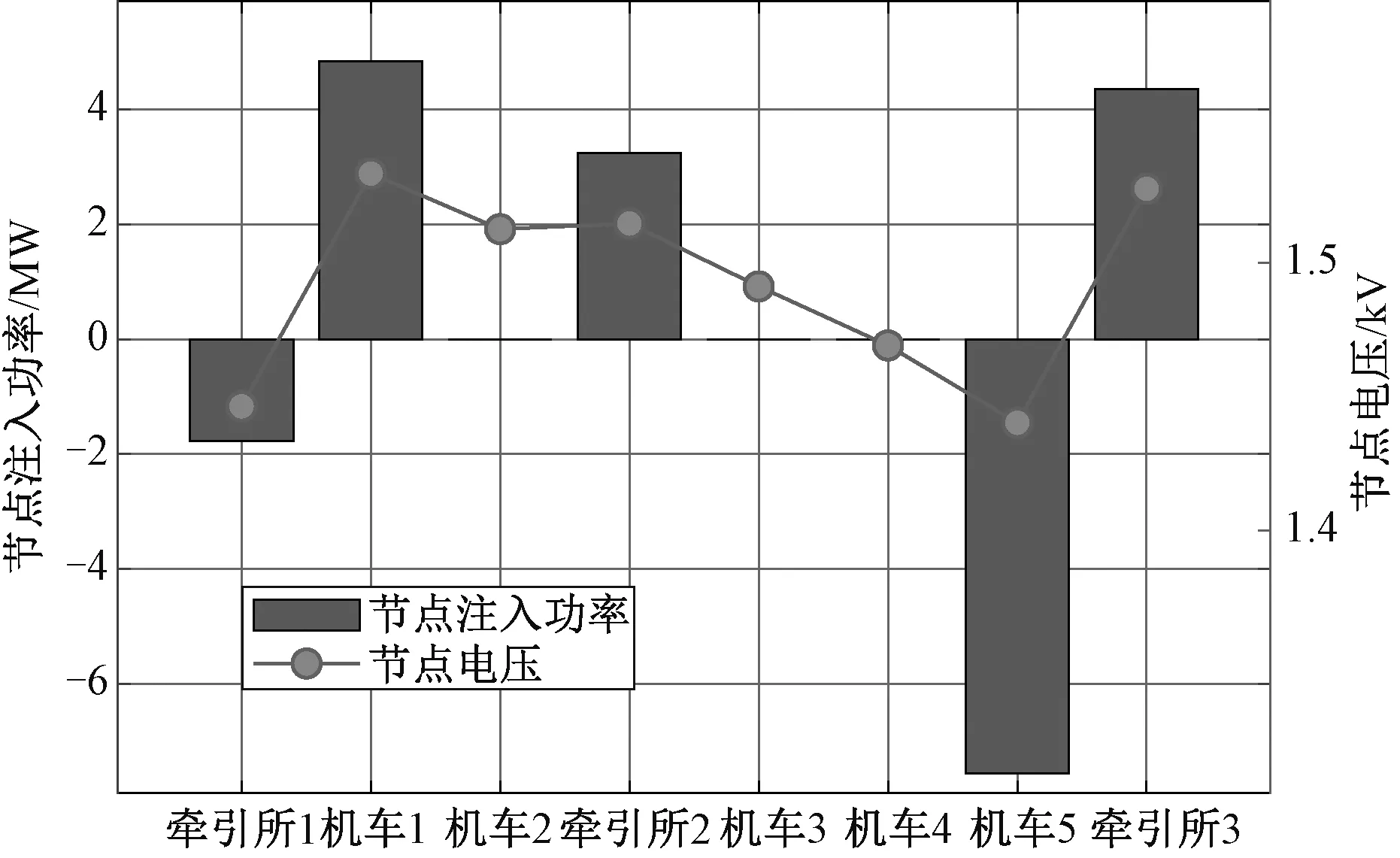
图6 局部区域潮流计算结果

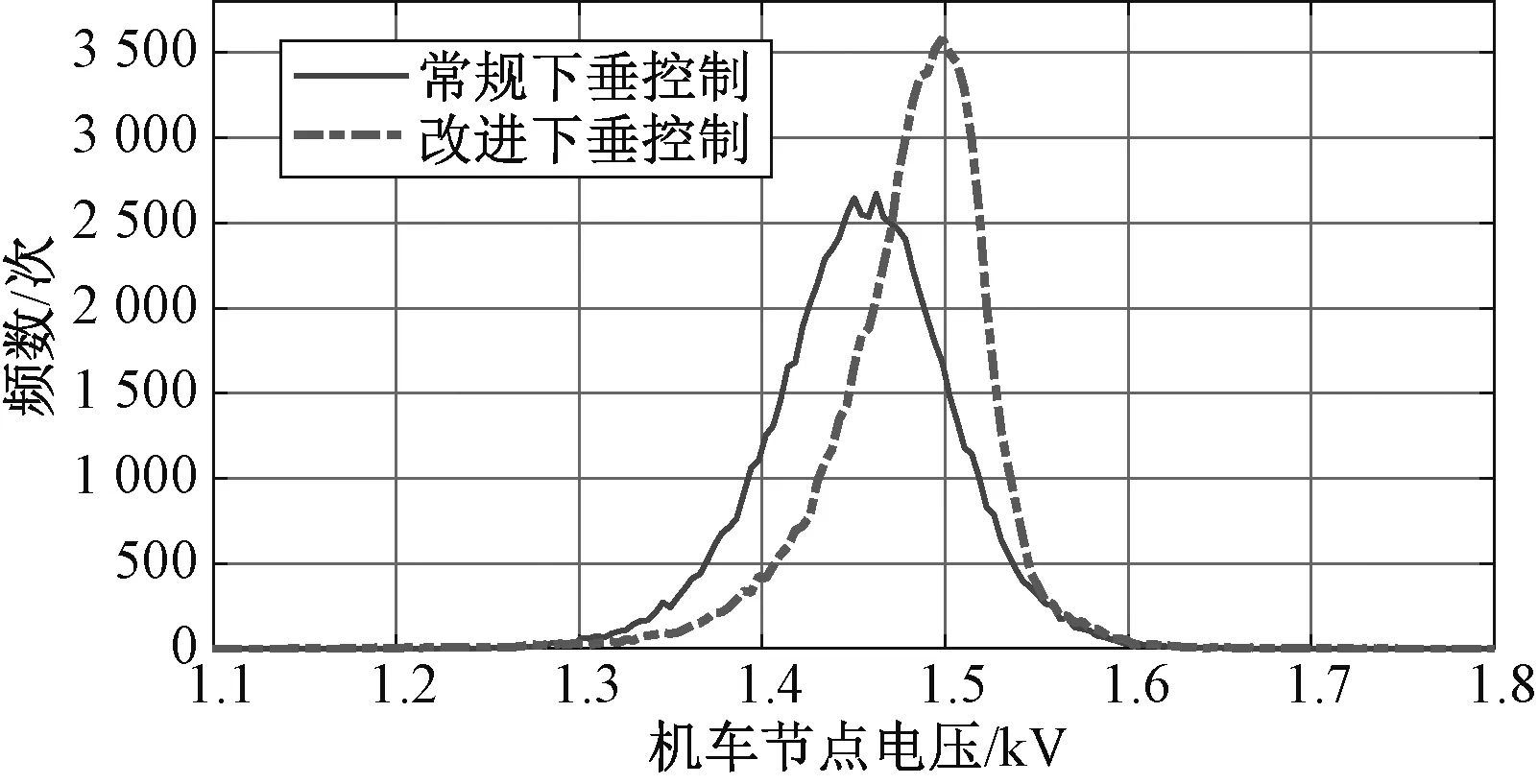
图7 机车节点电压统计分布直方图

图8 牵引所峰值功率对比图

根据计算结果统计整个系统的节能效果如表3所示。由于机车具有反送功率的能力，网损率定义为网络损耗与机车牵引能量之比。在节能效果上，两种控制方式没有显著区别。

表3 节能效果比较分析

从上述潮流计算结果可以看出，本文所提潮流计算方法能够有效体现系统级控制策略的影响，给出牵引所、接触网的电压和功率分布结果。

4 结论

(1)提出了一种计及系统级控制的VSC-TPSS潮流算法。以下垂控制为例，将牵引所建模为TSSU节点和TSSI节点，通过修改Ud和Rd模拟下垂控制的控制效果。引入阻尼因子α解决迭代中的收敛问题，通过更新迭代Ud和Rd完成计及系统级控制的VSC-TPSS潮流计算。

(2)结合北京地铁16号线的实际情况，通过算例验证了算法的有效性，并根据潮流计算的结果对系统的经济技术性做了简要分析。由于本文提出的算法能够模拟各种系统级控制方式的控制效果，适用于完成各种控制或供电方式下TPSS的对比分析，因此具有很大的实用价值。

(3)本文提出的算法并不只适用于下垂控制，通过动态调整Ud和Rd的大小，可以适用于多种系统级控制的潮流计算，具有普遍意义。