单框架控制力矩陀螺输出特性分析1)

黄志来 李新圆 金栋平,2)

∗(南京航空航天大学航空学院机械结构力学及控制国家重点实验室,南京 210016)

†(安徽工业大学机械工程学院,安徽马鞍山 243002)

引言

傅科(Foucault)于1852 年首次提出“陀螺”概念[1],可利用陀螺的力学特性设计执行器,称之为控制力矩陀螺(control moment gyroscope,CMG).半个世纪以来,CMG 广泛用于航天器姿态控制[2],并随着航天器控制任务的多样化[3-4],从姿态控制逐渐延伸到能量存储[5]、振动抑制[6]等领域.

CMG 有两种机械结构,单框架(SCMG)[7]和双框架(double-gimbal control moment gyro,DCMG)[8].飞轮可调速时,CMG 演化成变速控制力矩陀螺(variable-speed control moment gyro,VCMG),按其机械结构分类,有单框架变速控制力矩陀螺(single-gimbal variable-speed control moment gyro,SVCMG)[9]和双框架变速控制力矩陀螺(double-gimbal variable-speed control moment gyro,DVCMG)[10-11].相比于DCMG,SCMG 机械结构简单,但存在奇异性问题,而前者机械结构和控制算法更加复杂,两者同属于多体系统,本文仅关注航天领域应用最广的SCMG.

通常,为实现航天器三轴姿态控制,在只利用SCMG 输出陀螺力矩[12]的情况下,要满足输出三维控制力矩,则需要按一定构型配置多个SCMG,如金字塔构型[13]、屋顶构型[14]和五棱锥构型[15]等.VSCMG 有两个输出,只需两个VSCMG 即可完成航天器三轴姿态控制.力矩陀螺群存在操纵奇异性[16]问题,针对不同构型的力矩陀螺群,许多学者分析了其奇异几何特性[17-18]和零运动存在性[19],提出诸如奇异逃离[20]、奇异鲁棒[21]、反馈[22]、方向规避等操纵律[23],以及综合零运动与奇异逃离的混合操纵律[24-25]等.

最初,SCMG 作为航天器的执行机构,其输出模型仅考虑陀螺力矩[26],而VSCMG 的飞轮可调速,输出力矩比SCMG 多一个反作用力矩[27].为分析柔性航天器的振动问题[28],胡权等[29]基于Kane 方程建立了适用于任意构型的多个柔性体系统递推算法,这丰富了含SCMG 的多体系统建模方法.现有研究对SCMG 的力矩输出特性不够关注,一直停留于Lappas等[30]关于SCMG 基座角速度较小且转子角速度较大的假设基础之上,并借鉴反作用轮原理获得SCMG的力矩放大效应[30-31].

本文不局限于Lappas 假设条件,建立SCMG 输出力矩模型,在全部可行域中对SCMG 输出特性进行解析,以期更加全面地理解SCMG 动态输出特性,为在工程实践中高效利用SCMG 及其控制策略设计提供新思路.

1 SCMG 输出力矩模型

如图1 所示,设SCMG 的连体坐标系为F(g,s,t),坐标轴单位矢量为s,g和t,其中g为安装轴.定义飞轮角速度和角动量分别为Ω和h,框架相对基座的转动角速度为˙δ,以致Ω=Ωs,h=hs,δ=δg和.在连体坐标系中,基座、飞轮和框架的角速度为

从式(2)可见,SCMG 输出力矩沿s,g和t三个方向,而仅有g和s两个方向具有输入力矩,即SCMG 为二维输入三维输出系统.

将式(2)输出力矩分成两部分,即τ=τ0+τc,这里τ0=τg0g+τs0s+τt0t为不可调控输出力矩,表示SCMG 对基座的惯性影响,只与基座角加速度和角速度有关,τc=τgcg+τscs+τtct为可调控输出力矩.令,则

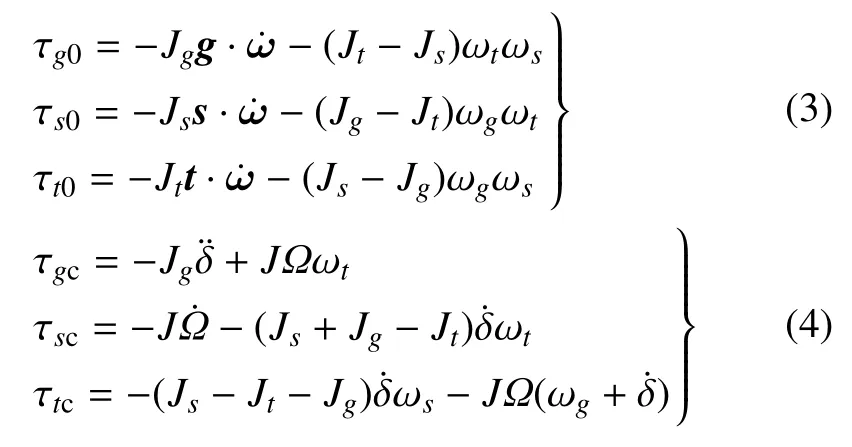
2 SCMG 输出输入力矩比

设输入力矩为

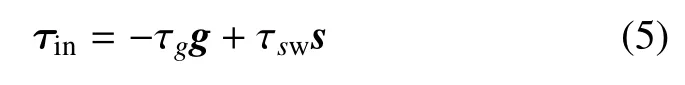
式中,τsw=−τs|Jfg=Jfs=Jft=0=.记输出力矩为τout,则输出与输入力矩比定义为

因此,当n1=1 且n2=n3=n4=0 时,意指SCMG；当n2=1 且n1=n3=n4=0 时,意指反作用轮；当n1=n2=1 且n3=n4=0 时,则代表VSCMG;当n1=n2=n3=1 且n4=0 或n1=n2=n3=n4=1 时,本文称为三维单框架控制力矩陀螺(three-dimensional single-gimbal control moment gyro,3D-SCMG).输出力矩可以为全部输出力矩、可调节输出力矩或者被利用输出力矩,即

选择合适的独立参数改写式(8),有

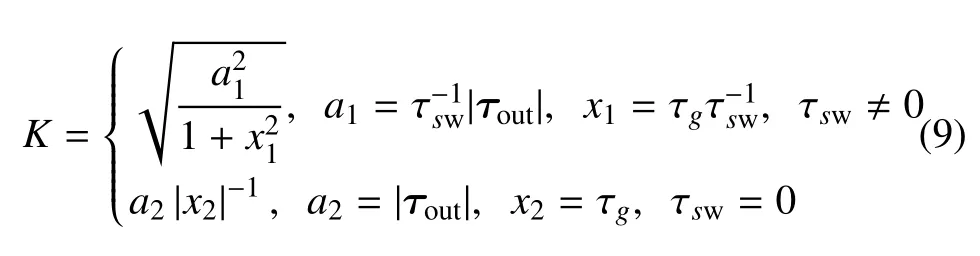
式中,a1为输出力矩幅值与s方向输入力矩比值,a2为输出力矩幅值,x1为g方向与s方向输入力矩比值,x2为g方向输入力矩.根据式(9),可得输出与输入力矩之比的关系曲线,如图2 所示.从图2 可知,K值与SCMG 的状态有关,并不恒大于1,即SCMG 并不总有力矩放大效应.

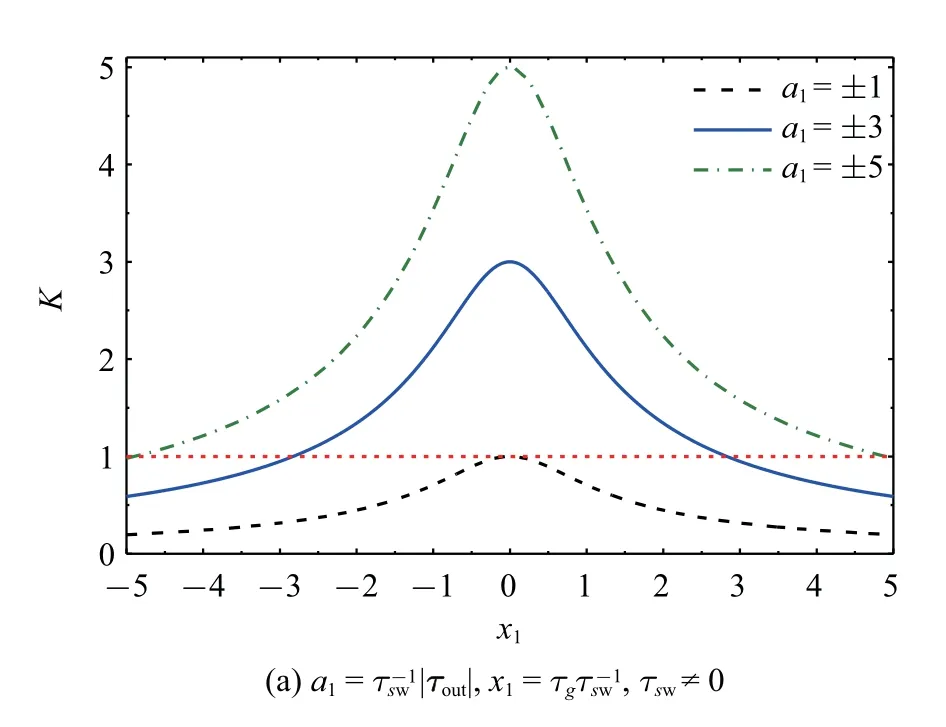
图2 SCMG 输出输入力矩比Fig.2 Torque ratio of SCMG’s input to output

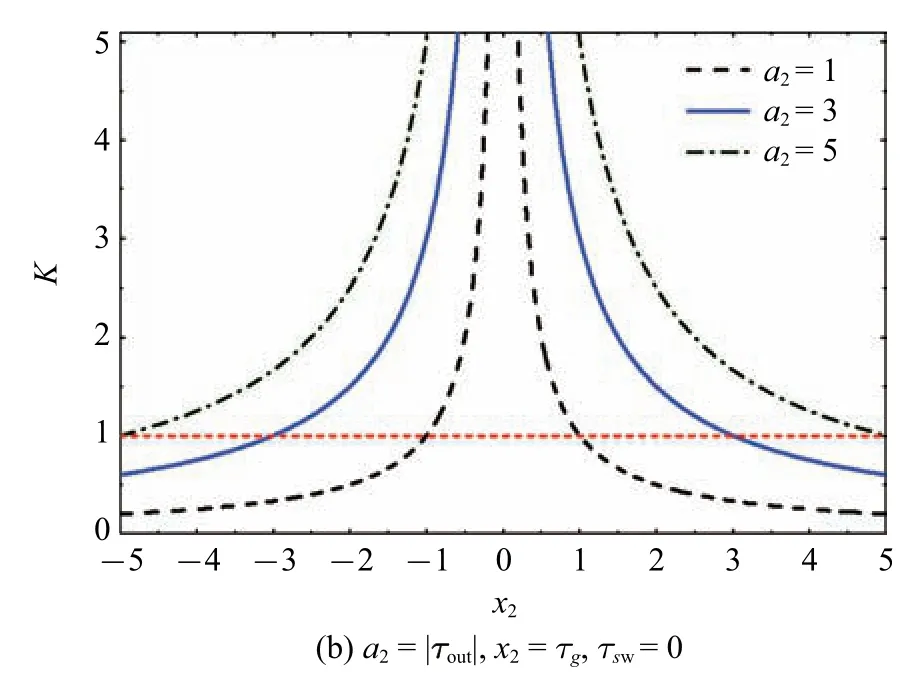
图2 SCMG 输出输入力矩比(续)Fig.2 Torque ratio of SCMG’s input to output(continued)

同理,可以选择合适的独立参数,对特定情形下的K值进行分析.这里例举基座固定、输出力矩为全部力矩和三维控制力矩陀螺.

(1)基座固定

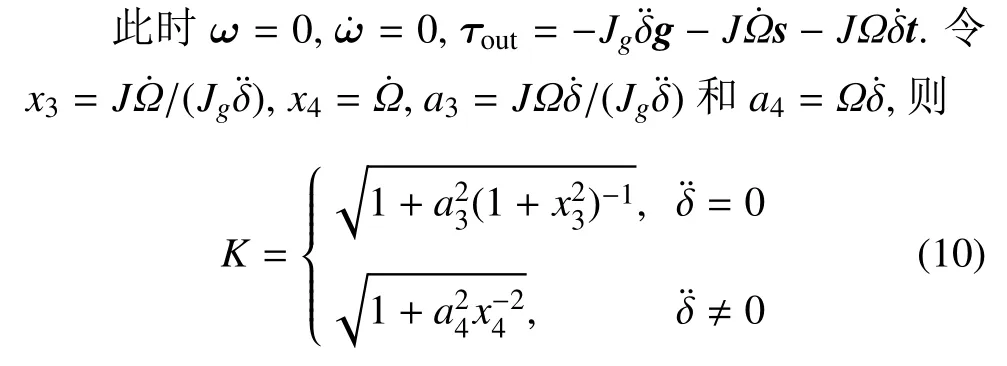
由式(10)可得SCMG 的输出输入力矩比曲线,结果如图3 所示.从图3 可见,基座固定的SCMG 输出与输入力矩比K≥1.当a3或a4为零时,K=1,此时τout中陀螺力矩为零,即等同于反作用轮.

(2)输出力矩为全部力矩

此时,输出力矩τout=τ,则

(3)三维控制力矩陀螺

三维控制力矩陀螺情形,即考虑τout=,n1=n2=n3=1 且n4=0,则

图3 基座固定的SCMG 输出输入力矩比Fig.3 Torque ratio of SCMG’s input to output with the fixed base

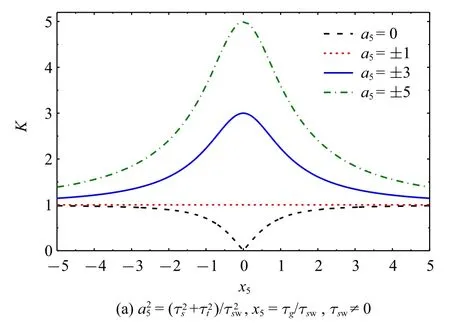
图4 SCMG 输出输入力矩比(τout=τ)Fig.4 Torque ratio of SCMG’s input to output with τout=τ

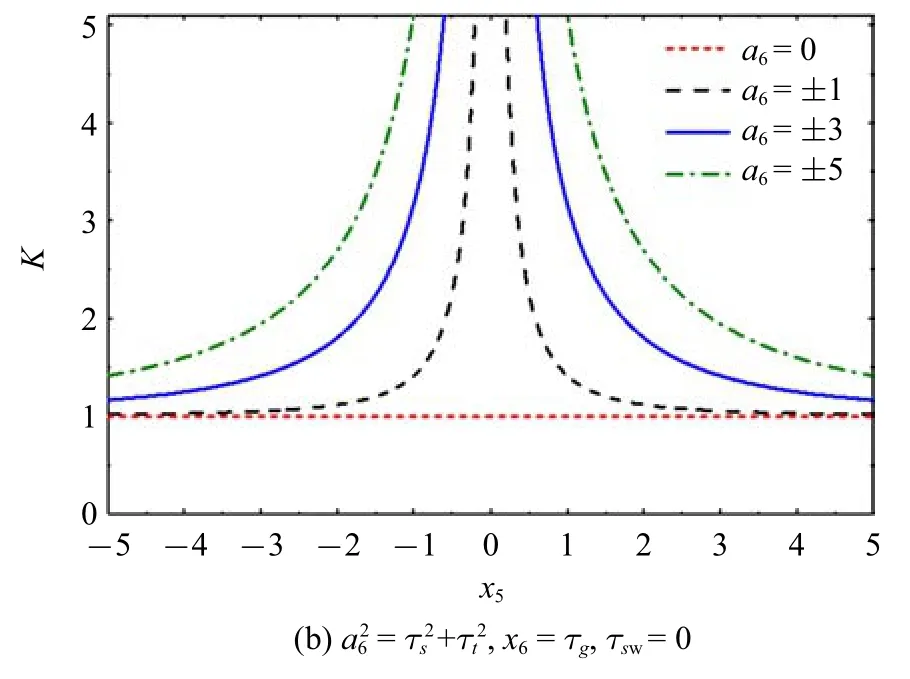
图4 SCMG 输出输入力矩比(τout=τ)(续)Fig.4 Torque ratio of SCMG’s input to output with τout=τ (continued)

3 SCMG 力矩利用率

图6 矢量几何关系Fig.6 Geometric relation diagram of vectors

式中,p1为基座的角速度在t方向分量与框架角速度值之比,p2为转子转速值与框架角速度值之比,n表示转子在s轴的惯量矩与基座主惯量矩之比.

根据式(23),当n=1 和n=2 时,ηm分别如图7所示.对比图7(a)和图7(b)可知,ηm曲线关于p2=0对称,并在p2=0 取得峰值,随|p1|值上升而下降.当|p1| >1 时,ηm始终小于1,可得此时η 恒小于1.n不影响峰值大小,但随n增大,使得ηm曲线的峰值变陡.

图7 SCMG 力矩利用率上界ηm(=0,==0,Jg= Js= Jt=nJ)Fig.7 The upper bound of torque utilization in SCMG(=0,==0, Jg= Js= Jt=nJ)

4 姿态控制

4.1 非对角奇异鲁棒操纵控制

考虑斜装两个VSCMG 的航天器姿态控制,安装角β=π/6,第i个SCMG 的转子对s轴转动惯量为Ji,其连体坐标系对航天器本体坐标系的转换矩阵为Bi(i=1,2).矢量或张量在航天器本体坐标系下的坐标加注上标(b),则陀螺群的输出力矩在航天器本体坐标系中的坐标为

选4 种控制参数进行控制效果考核,方案1:Wi=1,k=300;方案2:Wi=300,k=10;方案3:Wi=200,k=100;方案4:Wi=300,k=5.仿真控制结果如图8 和图9 所示.可以看出,4 种方案均在500 s 内趋于稳态,其中方案1 和3 在初始有一段时间的波动后趋于稳态,方案2 和4 相对平稳.

图8 航天器姿态四元数时间历程Fig.8 Time histories of the attitude quaternion about spacecraft

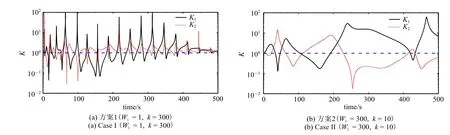
图10 输出与输入力矩比时间历程Fig.10 Torque ratio of CMG’s input to output vs time

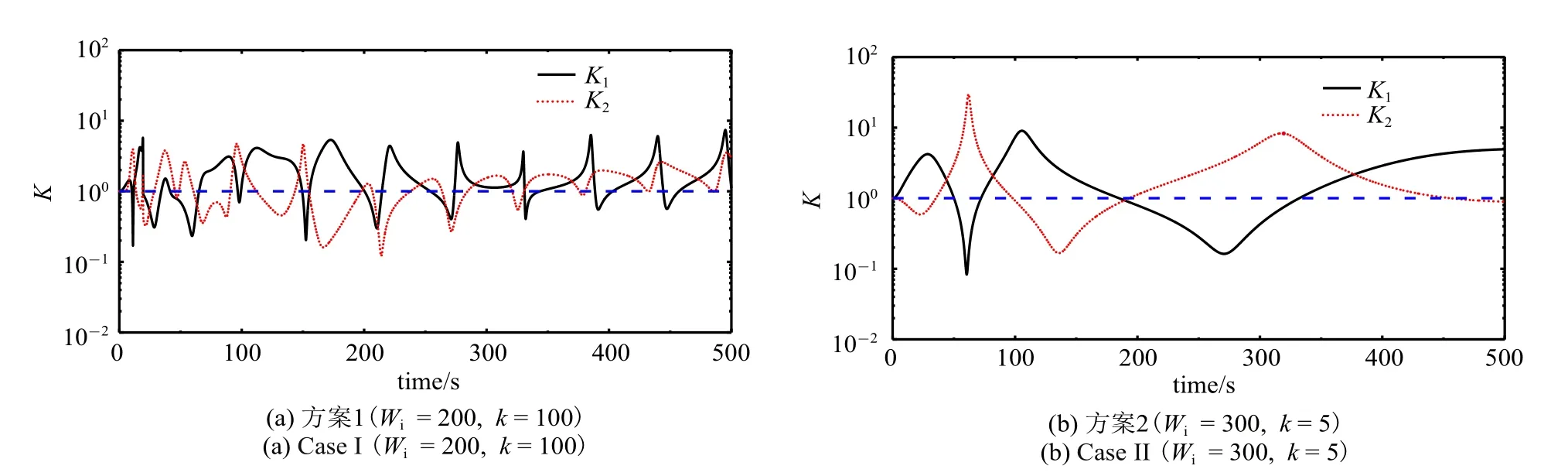
图11 输出与输入力矩比时间历程Fig.11 Torque ratio of CMG’s input to output vs time

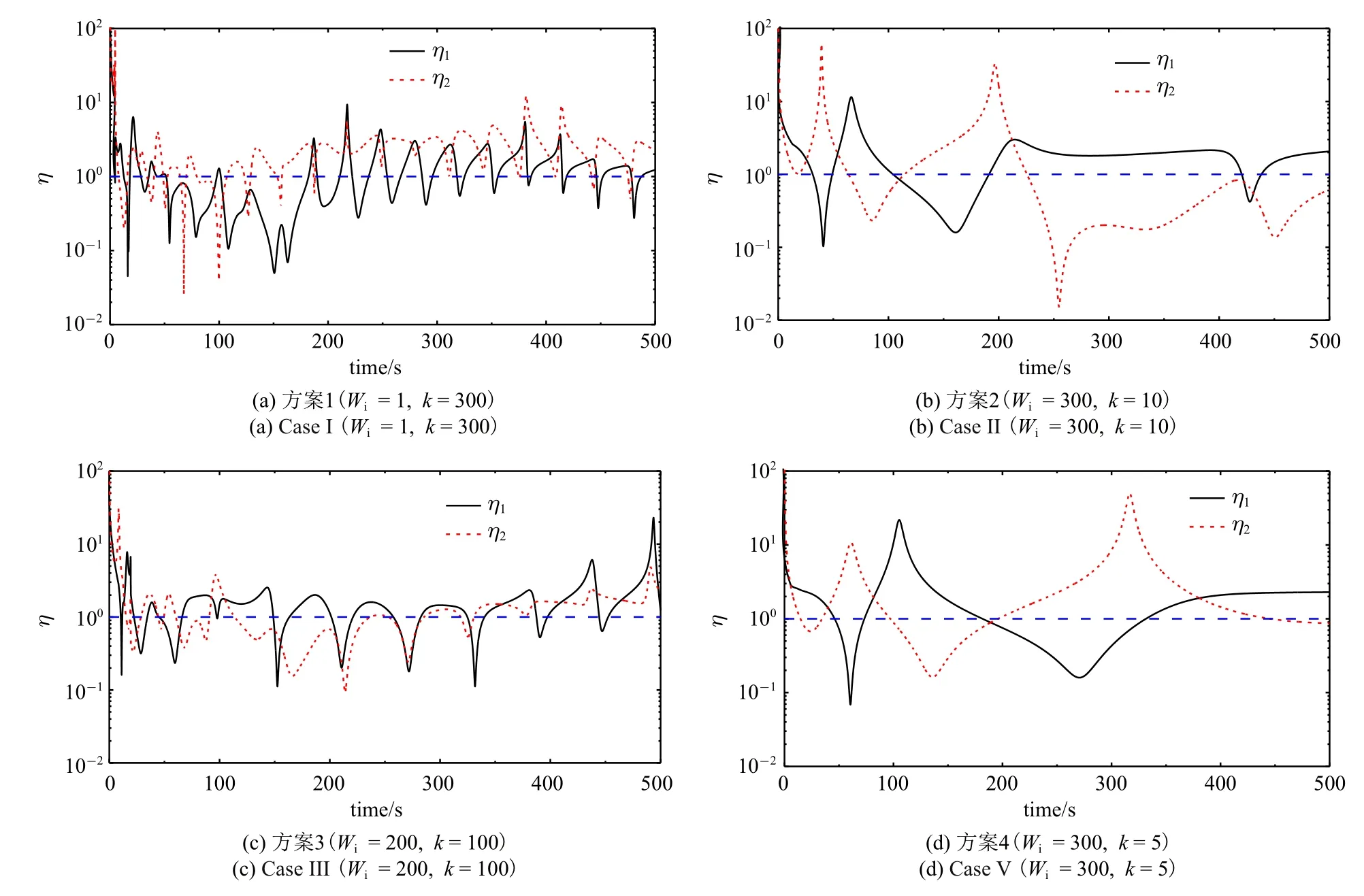
图12 力矩利用率时间历程Fig.12 Torque utilization vs time

由式(8)和式(20)可得SCMG 群的输出与输入力矩之比K和力矩利用率η,如图10～图12 所示.可以看出,在4 种方案中,K和η 均在等值线1 上下波动,表明SCMG 并不恒有力矩放大效应和高效的力矩利用率,这与理论结论一致.方案1 在等值线1上下波动次数最多,总体控制效果欠佳,与图8(a)和图9(a)表现出的控制效果吻合；方案3 在等值线1上下波动次数仅次于方案1,与图8(c)和图9(c)一致.从图10(b)和图11(b)可见,方案2 的输出输入力矩比在等值线1 以上的区域占优.根据图8 和图9 所示的控制效果,方案2 收敛更快,两者吻合；比较图12(b)和图12(d)可见,方案3 的力矩利用率η 在等值线1 以上的区域占优,与图8 和图9 所示的平稳控制效果一致.综上所述,控制效果与输出输入力矩比K和力矩利用率η 这两个参数密切相关.

4.2 优化控制

其中

式中,Ei表示i×i阶单位矩阵.方案1 控制效果如图13(a)和图14(a)所示,框架角速度和转子角加速度分别如图15(a)和图16(a)所示.由式(8)和式(20)计算输出与输入力矩比和力矩利用率,结果如图17(a)和图18(a)所示.

由式(3)和式(4)可知,SCMG 为三维力矩输出,单个SCMG 即可实现航天器三维姿态控制.因此,优化控制方案2 只保留优化方案1 中第一个SCMG,仿真时长tf=200 s,其他仿真参数不变.方案2 仿真控制效果如图13(b)和图14(b)所示,框架角速度和转子角加速度如图15(b)和图16(b)所示.从式(8)和式(20)可得输出与输入力矩比和力矩利用率,结果如图17(b)和图18(b)所示.

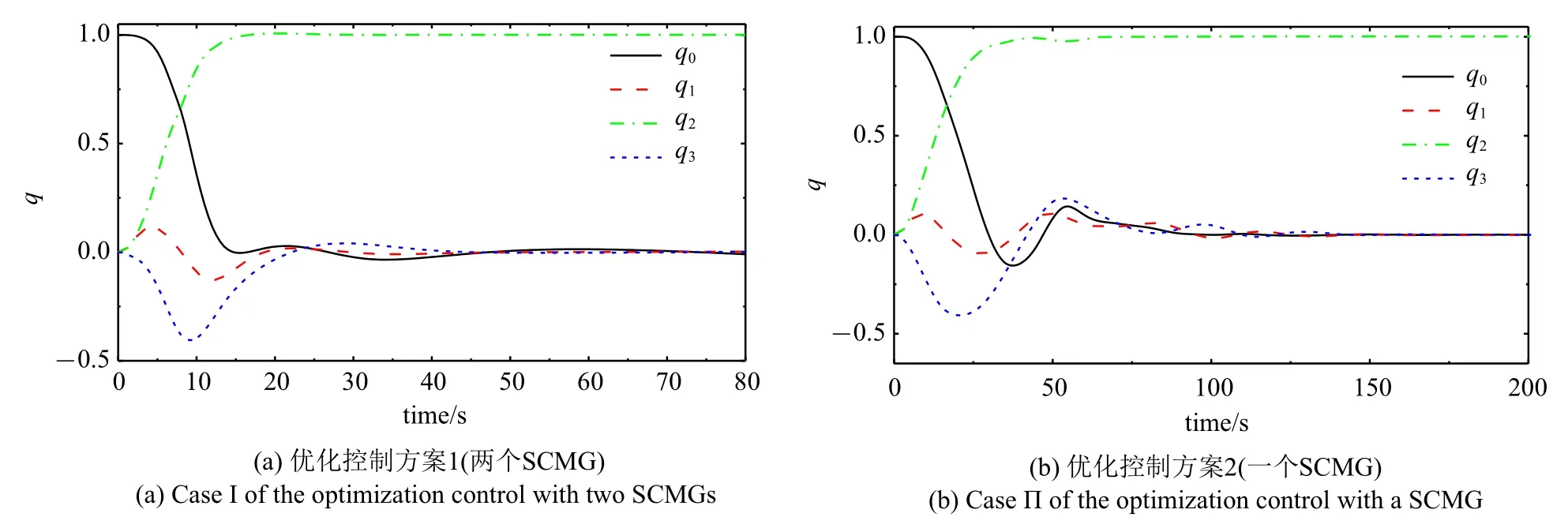
图13 航天器姿态四元数时间历程Fig.13 Time histories of the attitude quaternion about the spacecraft

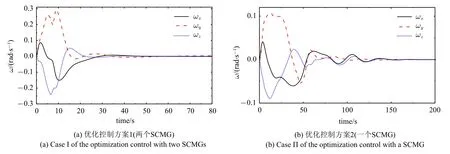
图14 航天器角速度时间历程Fig.14 Time histories of the angular velocity about the spacecraft

图15 框架角速度时间历程Fig.15 Time histories of the gimbal rates

图16 转子角加速度时间历程Fig.16 Time histories of the angular acceleration about the flywheel

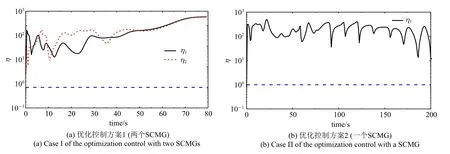
图18 力矩利用率时间历程Fig.18 Torque utilization vs time

从图13 和图14 可见,考虑到SCMG 的运动参数受限,两个优化控制方案均可完成控制任务,控制过程比较平稳,收敛效果良好.对于收敛到目标的耗时,方案1(两个SCMG)约50 s,方案2(一个SCMG)约150 s,后者用时略长,前者航天器机动角速度明显高于后者,因此收敛速度更快.从图15 可见,方案1 的框架角速度幅值更大.图15(a)显示方案1 在35 s 以后(i=1,2)已接近零,即此时输出的陀螺力矩值非常有限.由图16 可知,方案1 长时间利用转子变速输出力矩,而方案2 在50 s 时已接近目标姿态,之后就不再利用转子变速输出力矩,但维持比较高的转子速度.由图15(b)可知,方案2 在50 s 以后框架角速度在稳态期望值零上下波动,通过输出陀螺力矩来调节航天器姿态.上述两种优化控制方案的任务相同,但图13～图16 中两种控制方案表现出明显差异,根本原因在于方案1 有4 个输入,从控制的角度可理解其有一个冗余,可行域更广；方案2 仅有2 个输入,属于欠驱动,可行域更窄.由图17 和图18 可知,在整个控制过程中,两种优化控制方案的输出输入力矩比和力矩利用率始终位于等值线1 以上,表明在优化控制过程中SCMG 始终有良好的输出特性,即SCMG 始终具有力矩放大效应和高效的力矩利用率.

5 结论

通过建立SCMG 的两维输入三维输出模型,将其输出力矩分解成可调控部分与不可调控部分,进而定义SCMG 的输入与输出力矩比和力矩利用率.研究发现,SCMG 不恒有力矩放大效应,也不恒有高效的力矩利用率.此外,SCMG 输出特性确实与系统状态有关.根据SCMG 的三维输出特性,借助一个SCMG 的优化控制可实现航天器三轴姿态机动.在提出的优化控制方案中,可以始终确保SCMG 具有力矩放大效应和高效的力矩利用率.因此,通过合理设计控制方案,可以使SCMG 具有良好的动态输出特性且控制效果最优.