风剪切对风力机叶片气动性能及尾迹形状的影响1)

许波峰 朱紫璇 戴成军 蔡 新 王同光 赵振宙

∗(河海大学可再生能源发电技术教育部工程研究中心,南京 210000)

†(河海大学江苏省风电机组结构工程研究中心,南京 210000)

∗∗(南京航空航天大学江苏省风力机设计高技术研究重点实验室,南京 210000)

引言

风力机运行在大气边界层中,其叶片性能会受到风剪切的影响.在风剪切入流条件下,风轮旋转平面速度分布不均匀,叶片载荷呈周期性变化,风力机的性能也会有所降低[1].此外,从叶片尖部拖出的尾流的畸变会反过来作用于风轮平面,进一步影响叶片气动性能.随着机组的大型化发展,风剪切对风力机叶片的影响会更加明显.

风力机叶片的气动性能计算方法主要有动量−叶素理论(blade element momentum,BEM)方法、CFD方法、自由涡尾迹方法.BEM 方法在科学研究与工业领域得到了广泛应用,对于非定常入流条件下的仿真需要加入相关修正模型来提高计算精准度[2-7].唐新姿等[8]基于修正的BEM 和非嵌入式概率配置点法,提出了一种风力机不确定空气动力学法,研究了不确定性风速对风力机的影响.Ali 等[9]采用一种经验非定常BEM 计算高空风力机气动特性,在峰值工况运行下的性能与CFD 方法结果相比,其偏差在4.1%以内.但在风轮平面上的入流分布明显不均匀的情况下,气动载荷的计算会有较大的偏差[10].CFD 方法的计算精度优于BEM,不少学者采用CFD 方法做了非定常工况下风力机的相关仿真[11-12].但CFD 方法的一些参数设置会对计算结果有一定的影响,并且其流场区域网格的绘制费时费力,计算成本高.自由涡尾迹(free vortex wake,FVW)方法的计算精确度高于BEM 且计算量低于CFD 方法.许波峰等[13-14]研究了涡核尺寸对FVW 方法准确预估气动性能的影响,保证了该方法的精确性.FVW 方法在非定常工况下的研究较多[15-17],仿真结果较好.因此采用自由涡尾迹方法来计算风剪切下的气动性能具有一定的优势.

考虑风剪切的作用对风力机的设计有着重要作用,Kavari 等[18]基于BEM 研究了风剪切对叶片设计的影响,叶根所受影响不大,而大部分变化发生在叶片长度的0.2 到0.8 之间.对风剪切作用下气动性能研究十分重要,张旭耀等[19]研究了风剪切来流下水平轴风力机流场特性与风轮气动载荷的分布规律;Shen 等[20]采用升力面法和FVW 方法计算了风剪切入流下风力机的气动载荷.这些研究都指出叶片载荷变化呈现周期性波动,Chen 等[21]基于自由涡尾迹模型和精确梁理论的气动弹性模型研究了利用后掠叶片进行被动载荷控制的方法来减轻载荷变化.除了对气动性能进行分析,王海鹏等[22]研究了风剪切对风力机近尾迹流动特性的影响;也有学者研究对比了定常和风剪切情况下的尾迹结构形状,风剪切下尾迹呈现出不对称的现象[23-24].FVW 方法不仅能够精确快速的计算出风剪切条件下的非定常气动特性,还能够反映尾迹与风轮平面之间的作用.Shaler等[25]分析了风力机尾迹对其他风力机作用的影响,其功率与叶片弯矩的不稳定性增大.Su 等[26]使用混合FVW 方法探讨了利用倾斜尾迹的转向来减轻对下风向风力机发电潜力影响的问题.Jeong 等[27]采用BEM 方法与FVW 方法研究出风力机在风剪切和紊流条件下会受到不利的空气载荷和叶片变形,同时得出了在较低的风速下尾迹对叶片的气动和结构性能有明显的影响,因此需要对尾迹动力学进行准确评估的结论.

不同的风剪切因子会对叶片气动性能和尾迹形状的畸变产生不同程度的影响,同时,尾迹的不对称除了对其下游的风力机产生影响外,它对自身风轮叶片也存在诱导作用,具有一定的研究价值.风轮旋转平面速度分布是来流风速与诱导速度之和,来流风速主要受风剪切影响,诱导速度来源于叶片附着涡与尾迹涡的作用.为了研究风剪切作用下倾斜尾迹对叶片气动性能的影响大小,本文采用一种“D3P3”格式的时间步进自由涡尾迹方法[28],重点在于研究风剪切作用下尾迹形状的畸变对叶片流场的影响,因此建立了两种尾迹模型,即剪切入流+叶片附着涡+倾斜尾迹与剪切入流+叶片附着涡+对称尾迹,其示意图如图1 所示,并计算两种模型作用下的叶片气动性能,为风力机安全性设计和优化设计提供一定的依据.

图1 两种尾迹模型示意图Fig.1 Schematic diagram of two wake models

1 计算方法

1.1 自由涡尾迹模型

风轮坐标规定如图2 所示,z轴为风轮旋转轴,以下风向为正,y轴竖直向下,x轴与y,z轴符合右手法则.

图2 自由涡尾迹模型Fig.2 Free vortex wake model

采用Weissinger-L 升力面模型建立叶片的气动模型,如图2 所示.由置于1/4 弦线处的附着涡线代替叶片,并按“arccos 余弦法”将其离散成一系列直涡线段,每段附着涡环量由对应叶素的气动特性及Kutta-Joukowski 定理确定.附着涡在空间和时间上的变化分别采用尾随涡和脱体涡来表示,从附着涡线节点处拖出.叶素控制点位于叶素中线的3/4 弦点处,涡线对叶素控制点和涡线节点的诱导速度由Biot-Savart 定律[29]确定,涡线周向诱导速度采用Lamb-Oseen 涡核模型修正[29]来避免产生奇点.叶片尾迹被划分为近尾迹和远尾迹,近尾迹在寿命角为60◦[30]处截断,远尾迹由叶尖涡组成,长度为风轮直径的两倍.涡线的控制方程偏微分形式为

式中,r是涡线节点的矢量位置,ψ 是叶片旋转时的方位角,ζ 是寿命角,Ω 是风轮转速,V∞是自由流速度,Vind是流场中所有涡线对该节点的总诱导速度.

自由涡尾迹的尾迹求解方法分为松弛迭代法、时间步进法两种.时间步进法能够计算出尾迹随时间不断发生形状和位置的变化,用于风剪切条件下风力机气动性能的计算更为合适.对于空间步(ζ)采用五点中心差分法,对于时间步(ψ),采用三步三阶预估—校正格式—-“D3P3”格式[28].

计算风剪切作用下的气动性能及尾迹形状时需要考虑到失速延迟现象和动态失速现象,因此采用Du-Selig 三维旋转效应模型[31]和Leishman-Beddoes动态失速模型[32]进行修正来提高计算的准确性.

1.2 风剪切入流模型

地表上空0～2000 m 存在大气边界层,风速在这个范围内会随高度z的变化而变化,根据IEC 标准,建立正常风廓线模型,速度可表示为

式中V(z)为高度z处的风速,Vhub为轮毂高度处风速,zhub风力机轮毂高度,α 为风剪切因子.

计算过程中方位角步长取10◦[33-34],将风轮旋转平面的径向方向和方位角方向被划分为36 份,每个节点的速度可用式(3)来表示

式中(l,i)表示风轮平面上某一点的坐标,l为径向方向,i为方位角方向,j表示时间步步数,z(l,i)表示某一点的高度,V(j,l,i)为风轮平面内某一点在x,y,z方向的风速.

尾迹位置使用“D3P3”格式迭代更新的过程中,尾迹节点的速度计算式为

式中UBOD为附着涡对该节点的诱导速度,UTIP为叶尖涡对该节点的诱导速度,UTRD为尾随涡对该节点的诱导速度,USHD为脱体涡对该节点的诱导速度.

1.3 计算流程

根据自由涡尾迹模型及风剪切模型,该方法的计算流程图如图3 所示.其中几何残差用新旧尾迹各节点坐标的均方差表示

式中jmax=NT,kmax=NTNC,NT为每一圈的时间步数,NC为整个尾迹的圈数.

2 模型验证

采用自由涡尾迹模型计算稳态入流条件下NREL Phase VI 风力机的气动性能及尾迹形状,并与实验数据[35]进行对比.主要计算7 m/s 和13 m/s 风速下叶片沿展向分布的法向力系数Cn和切向力系数Ct以及不同风速下的载荷.因为目前主流风力机都是变桨变速型,大风速下会通过变桨来控制叶片的迎角,一般不会处于深失速状态,而Phase VI 为失速型风力机,大风速下处于深失速状态,气动特性难以准确预估,所以模型验证中不考虑大风速下的气动性能.

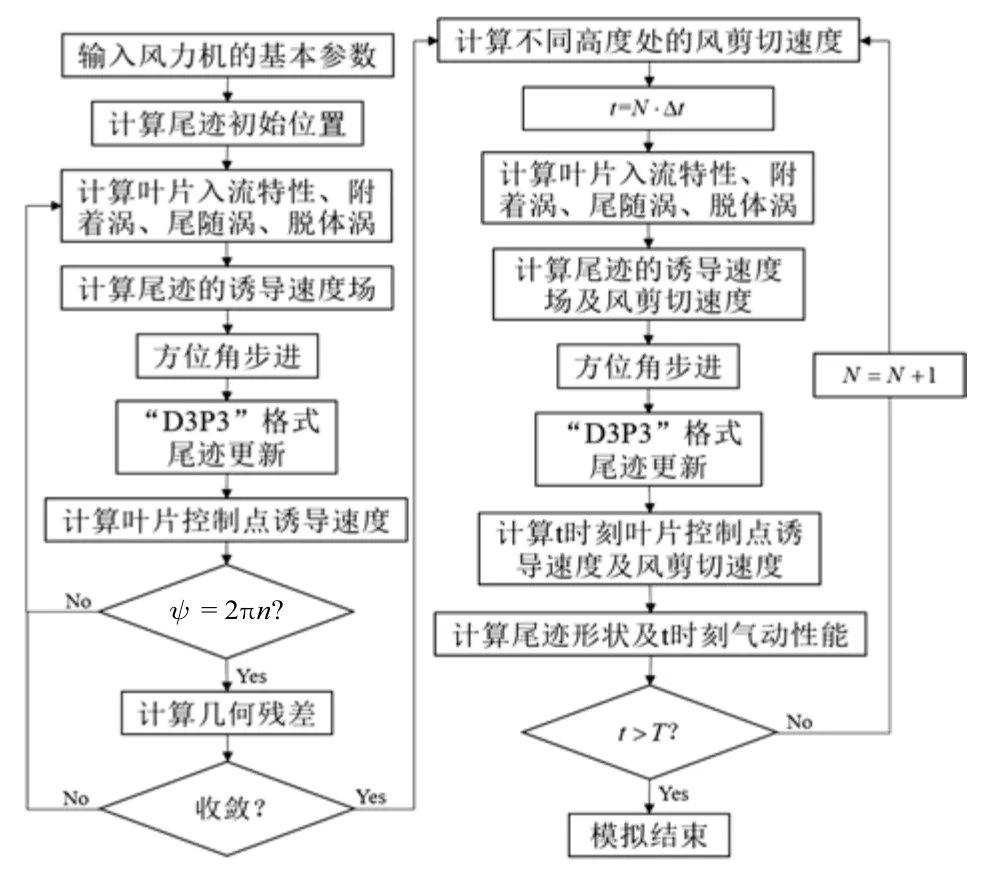
图3 时间步进自由涡尾迹法流程图Fig.3 Flow chart of time-marching free vortex wake methodology

7 m/s 风速下计算结果如图4 所示,该方法计算得到的法向力系数、切向力系数与实验数据误差较小,计算结果较为精确.图5 为13 m/s 风速下计算得到的气动力系数,可以看到叶根处的计算结果与实验数据的误差较大,这是由于叶根相比于叶片其他位置更容易进入失速状态,其周围的流体分离使得流场变得复杂,气动载荷的误差则会增大.从叶中至叶尖,法向力系数、切向力系数的计算结果与实验结果基本吻合.

图4 7 m/s 风速下的法向力系数与切向力系数Fig.4 Normal force coefficient and tangential force coefficient under 7 m/s wind speed

图4 7 m/s 风速下的法向力系数与切向力系数(续)Fig.4 Normal force coefficient and tangential force coefficient under 7 m/s wind speed(continued)

图5 13 m/s 风速下的法向力系数与切向力系数Fig.5 Normal force coefficient and tangential force coefficient under 13 m/s wind speed

图6 为不同风速下风力机推力和转矩的计算值与实验值的对比.可以看到随着风速的增大,风轮总体气动载荷的变化趋势与实验数据保持一致,10 m/s风速以下计算结果与实验值高度吻合,10 m/s 风速以上由于叶根出现了部分失速现象,法向力和切向力预测存在偏差,导致总体气动载荷计算存在一定的误差.

图6 不同风速下的推力和转矩Fig.6 Thrust and torque at different wind speeds

在叶尖速比为10,桨距角为4◦的条件下,尾迹形状的输出及其与实验结果的对比如图7 所示,可以看到自由涡尾迹方法能够很好地仿真出尾迹结构,说明它能够研究风剪切下尾迹形状的变化.

总的来数,上述的计算结果大部分在误差范围内,所以该自由涡尾迹模型能够用于研究风轮的气动载荷及尾迹形状.

3 风剪切下叶片的气动性能与尾迹形状

采用973 项目“大型风力机的空气动力学基础研究”中1.5 MW 风力机[36].该风力机的叶片数目为3,轮毂高度65 m,风轮直径83 m,额定转速17.2 r/min.在风力机运行的环境中,风剪切因子会受地形、粗糙度、温度、季节、时间等各种因素影响,它的取值可以在0.1～0.5 之间[37-38].本文计算的入流条件为:轮毂高度处风速为额定风速10.4m/s,此时风轮转速为额定转速,风剪切因子分别取0.1,0.2,0.3,0.4,0.5,其入流风速随高度的变化如图8 所示.随着风剪切因子的增大,风速在风轮平面最高点和最低点的速度差会随之增大,当α 为0.1 时,风速差达1.5 m/s;当α为0.5 时,风速差达7 m/s.

图7 尾迹形状验证Fig.7 Verification of wake shape

图8 不同风剪切因子下的入流情况Fig.8 Inflow conditions under different wind shear coefficients

3.1 风剪切作用下的气动性能

图9 不同风剪切因子下的法向力系数和切向力系数Fig.9 Normal force coefficient and tangential force coefficient under different wind shear coefficients

风力机在风剪切作用下的实际气动性能会影响到发电量和风力机的运转,因此需要对该工况下气动性能进行分析以便为风力机的叶片设计提供相关依据.图9 为风剪切因子从0.1 至0.5 条件下,叶片在80%截面处的法向力系数和切向力系数.可以看出风剪切的作用使气动力系数随时间做周期性波动,这与入流风速在高度上的不均匀分布及叶片旋转过程中经过风轮平面的最低点与最高点有关,这些波动会使风力机承受疲劳载荷从而影响其安全性及使用寿命,风力机在设计过程中考虑风剪切作用显得十分重要.随着风剪切因子的增大,气动力系数的波动幅度明显变大,α 在0.1,0.3,0.5 时的波动幅度分别为0.1,0.29,0.51,风力机在设计时应充分考虑所选厂址的风剪切因子来进行设计.

图10 为风剪切因子从0.1 至0.5 条件下风力机所受的推力.随着风剪切因子的增大,风力机所受推力平均值逐渐减小,推力波动更为剧烈,说明风剪切较大的叶片机组与无风剪切作用下相比,无论是平均值还是波动幅值都相差较大.因此,风力机的设计更应该准确计算风场的风剪切因子并考虑风剪切因子对载荷的影响.

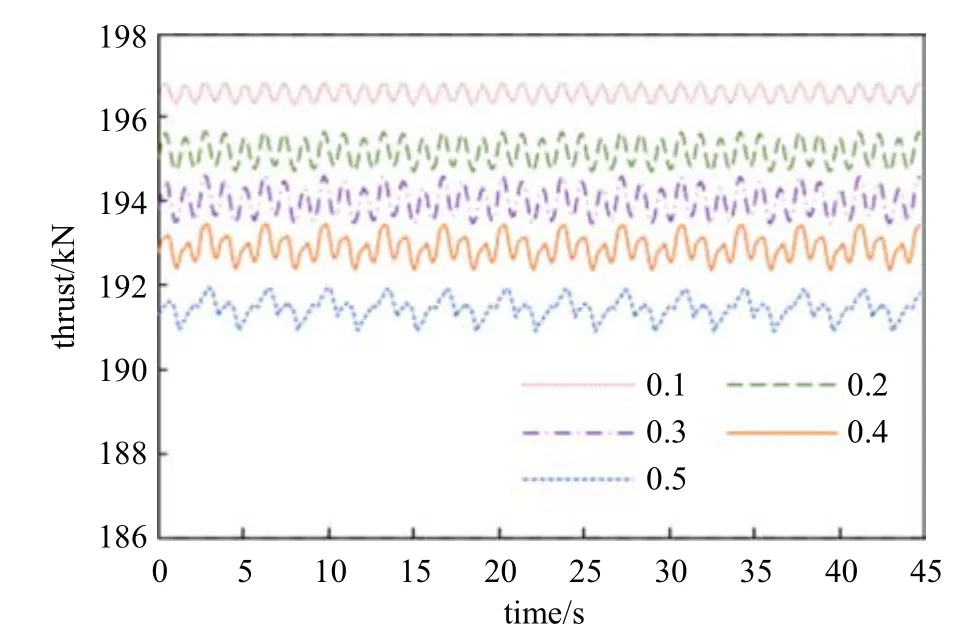
图10 不同风剪切因子下的推力Fig.10 Thrust under different wind shear coefficients

3.2 风剪切作用下尾迹形状的变化

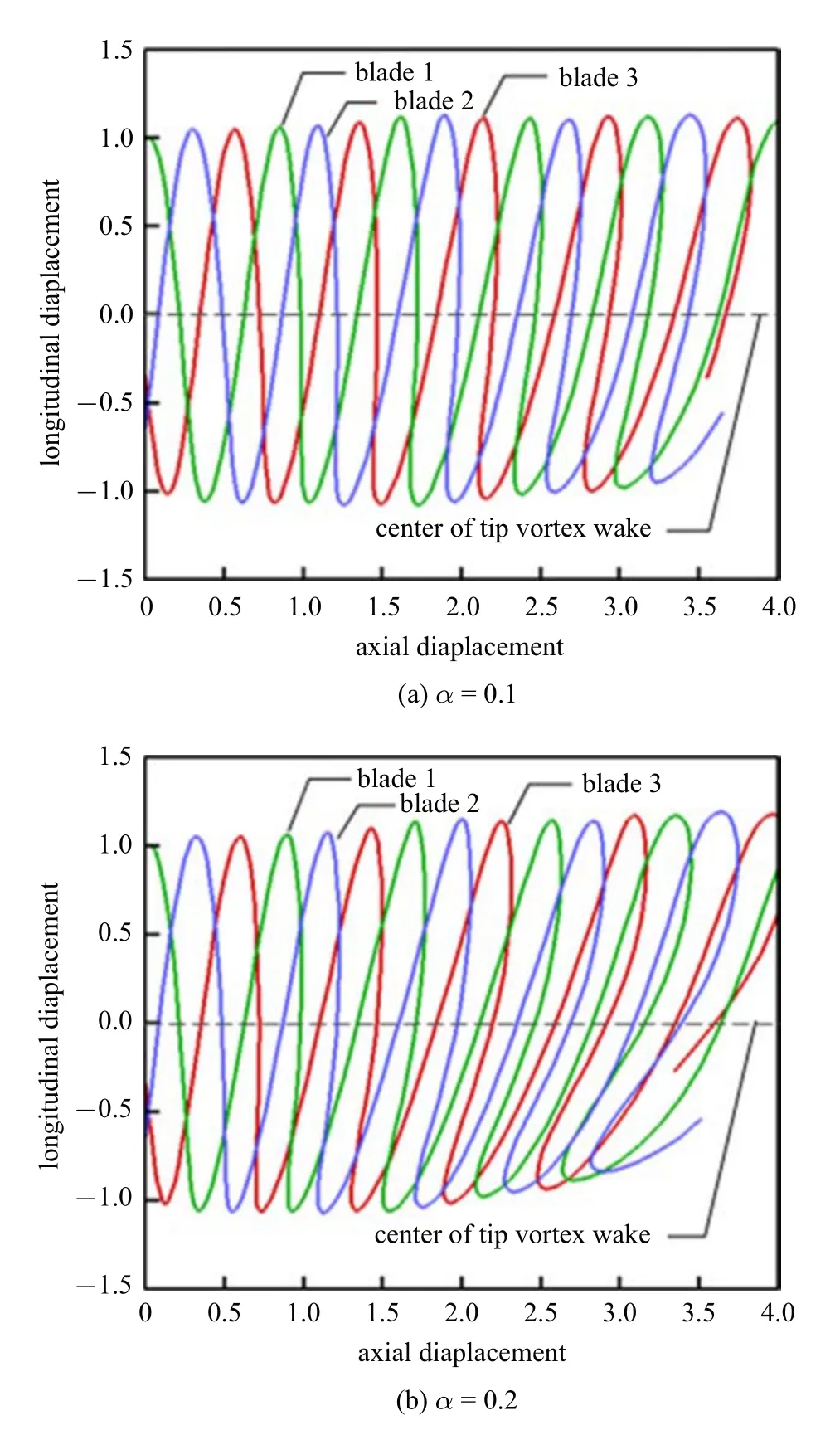
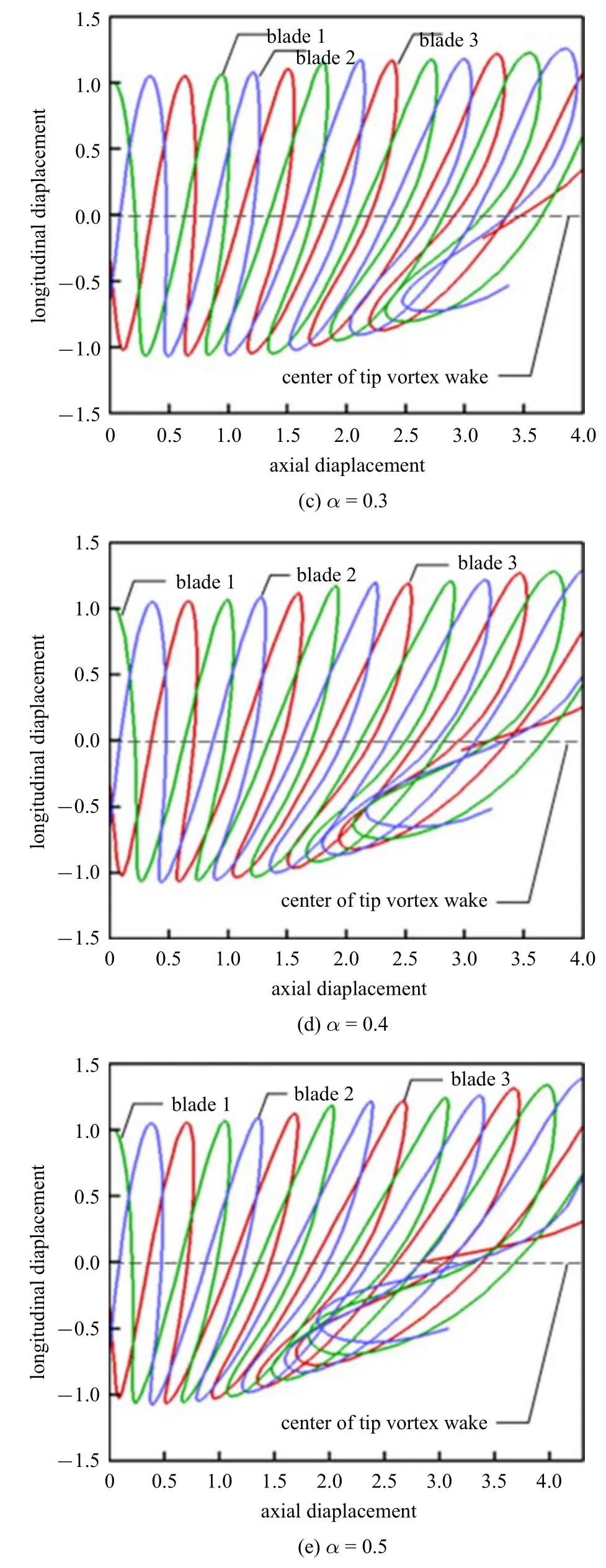
图11 不同风剪切因子的尾迹形状Fig.11 Wake shape under different wind shear coefficients

在给定的入流条件下,计算了不同风剪切因子作用于风力机后的叶尖涡尾迹形状,如图11 所示,3 种不同颜色分别代表了3 个叶片的尾迹.从图示结果可以看出风剪切的存在会使叶尖涡尾迹呈现出不对称、倾斜的形状.根据本文规定的坐标系,在风剪切的作用下,y轴负半轴所受的来流风速大于正半轴所受的来流风速,转动到负半轴的尾迹节点的运动速度更快一些,因此会出现图示所示的倾斜形状.从计算结果可以看到随着风剪切因子的增大,尾迹的不对称现象和倾斜程度更加显著,α 在0.4 和0.5 时远尾迹会出现向上卷起的现象,这些都与风轮平面最高与最低风速差的增大有关.

图12 给出了不同风剪切因子作用下,叶片1 尾迹在第4 圈的最低点和最高点的轴向相对位置.由图可得出,随着风剪切因子的增大,最低点的轴向相对位置逐渐减小,而最高点的轴向相对位置逐渐增大,即尾迹的倾斜程度越来越明显.

图13 叶片1 尾迹的第1 圈和第4 圈最低点距尾迹中心线的相对位移Fig.13 Relative displacement of the lowest point in the first lap and the fourth lap of the wake of blade 1 from the centerline

图13 给出了不同风剪切因子作用下,叶片1 尾迹在第1 圈和第4 圈的最低点距离叶尖涡尾迹中心线的相对位移.由图可得出,第1 圈最低点距中心线的相对位移基本不变,而随着风剪切因子的增大,第4 圈最低点距中心线的相对位移逐渐减小,说明尾迹向上卷起的现象越明显.

3.3 对称尾迹与倾斜尾迹下的气动性能

风剪切作为来流风速,对风力机叶片气动性能产生一定的影响,同时,其导致的畸变倾斜的尾迹会反过来作用于风轮平面.为了研究倾斜尾迹对风力机叶片气动性能的影响,建立了如图1 所示的两个尾迹模型进行对比,尾迹分别为风剪切作用下的真实倾斜尾迹与假设来流风速均等于轮毂处风速且无风剪切的虚拟对称尾迹,两种模型下的入流风均为剪切风.

首先计算了α 为0.3 时,倾斜尾迹和对称尾迹分别作用下风轮旋转平面的轴向诱导速度因子分布情况,如图14 和图15 所示.可以看到倾斜尾迹对风轮平面的诱导速度因子存在明显的不对称现象,而对称尾迹对风轮平面的诱导速度因子的分布较为均匀.

图16 给出了α 为0.3 时,叶片80%截面处在对称与倾斜尾迹诱导作用下的法向力系数和切向力系数.从图中的计算结果来看,无论尾迹是对称的还是倾斜的,在风剪切来流条件下都会呈现出随时间的周期性波动.对称尾迹下法向力系数与切向力系数的标准差分别为0.098 48 和0.028 45,倾斜尾迹下法向力系数与切向力系数的标准差分别为0.111 13 和0.031 73,可见,对称尾迹作用下的气动力系数波动幅度比倾斜尾迹的波动幅度小.尾迹在轮毂下方的倾斜程度更加明显,所以可以看到图中气动力系数在波谷的偏差比波峰的大.图17 为两种尾迹作用下气动力系数在波谷处的值的大小,即叶片转至向下时80%截面处气动力系数的对比.随着α 的增大,对称尾迹与倾斜尾迹对风轮最下方叶片尖部的气动载荷影响差别越明显,说明尾迹越倾斜,风轮旋转平面处的载荷不对称性越明显.

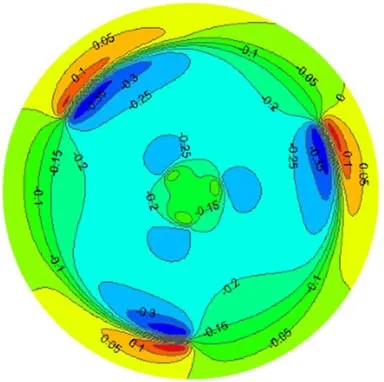
图14 倾斜尾迹对风轮旋转平面的轴向诱导速度因子Fig.14 Effect of tilted wake on axial induced velocity factor of wind turbine plane

图15 对称尾迹对风轮旋转平面的轴向诱导速度因子Fig.15 Effect of symmetrical wake on axial induced velocity factor of wind turbine plane

图16 对称与倾斜尾迹下的法向力系数和切向力系数Fig.16 Normal force coefficient and tangent force coefficient under the influence of symmetrical and tilted wake

图17 两种尾迹的法向力系数和切向力系数在不同风剪切因子下偏差Fig.17 Deviation of normal force coefficient and tangential force coefficient of two kinds of wake under different wind shear coefficients

图18 为α 为0.3 时,对称与倾斜尾迹作用下的推力.由图中结果可知,无论是倾斜尾迹还是对称尾迹的诱导,在风剪切作用下推力都呈现出随时间的波动.对称尾迹诱导下风力机所受的推力大于倾斜尾迹下风力机所受的推力,说明尾迹的变形会使风力机的总体性能减小且偏离较大,所以在风力机设计时需要考虑到尾迹变形对风力机性能的影响.

因此,在计算风剪切作用下叶片的气动性能时,除了要准确计算风剪切对叶片入流的影响,还要准确预估倾斜的叶片尾迹形状.

图18 对称与倾斜尾迹作用下的推力Fig.18 Thrust under symmetrical and tilted wake

4 结论

本文基于时间步进自由涡尾迹方法仿真了风剪切入流工况及不同风剪切因子作用下,风轮平面气动性能以及尾迹形状的变化,同时拟定了一个对称尾迹来研究尾迹形状变化对叶片气动性能的影响.通过对比分析得到如下结论:

(1)风剪切入流条件下,风力机叶片叶素的气动特性及叶片所受推力都随时间做周期性波动.

(2)轮毂处风速相同的条件下,风剪切较大的叶片机组与无风剪切作用下相比,无论是平均值还是波动幅值都相差较大,随着风剪切因子的增大,风力机的气动特性波动的幅度越大,所受推力越小,同时,尾迹不对称、倾斜的形状会更加明显.

(3)相同入流条件下,倾斜尾迹与拟定的对称尾迹相比,风轮平面的轴向诱导速度分布不均匀,气动力系数的波动更大,风力机所受平均推力更小,且随着风剪切因子的增大,对风轮叶片尖部的气动载荷影响差别越明显.尾迹越倾斜,风轮旋转平面处的载荷不对称性越明显.

(4)风剪切作用下,要提高风力机动态载荷计算的精度,正确预估倾斜的叶片尾迹形状与准确的风剪切入流分布同样重要.