基于卷积神经网络的涵洞式直立堤波浪透射预测1)

赵西增 徐天宇 谢玉林 吕超凡 姚炎明,2) 解 静 常 江

∗(浙江大学海洋学院,浙江舟山 316021)

†(交通运输部天津水运工程科学研究所,天津 300456)

∗∗(天津水运工程勘察设计院,天津市水运工程测绘技术重点实验室,天津 300456)

引言

涵洞式直立堤一般指在胸墙位置处设置涵洞的重力式直立防波堤,其可连通港池内外的水体,避免港内出现泥沙淤积的情况,同时,波浪能量也可通过涵洞传入港池内部,影响港内的水动力特征以及泊稳情况.目前,众多学者对于涵洞式直立堤波浪透射问题的研究主要以理论分析、实验模拟及数值计算为主.文献[1]将Weigel 公式用于涵洞式直立堤波浪透射系数的计算,并基于实验结果提出了相应的修正系数以提高计算精度;文献[2]采用对称法结合特征函数对涵洞式直立堤的反射、透射系数进行了计算;文献[3]基于OpenFOAM 二次开发的CFD 求解器,对规则波作用下的涵洞内部水动力学特征进行了相关研究.但是,文献[4]指出由于波浪与直立结构物相互作用产生强湍动掺气水流,使其研究过程十分复杂.

近年来,随着机器学习技术的发展,传统水动力学问题迎来了新的求解理念.目前,已有众多学者将机器学习算法应用于波浪相关问题的研究.文献[5]采用BP 神经网络对波浪发电系统的输出功率进行计算.文献[6]基于GA-BP 神经网络对孤立波的爬高进行预测.文献[7]使用支持向量机以及神经网络对南海海域波浪的有效波高进行预测.文献[8]将神经网络应用于近岸岛屿海浪传播的模拟.

不同于传统的数值模拟方式,机器学习算法可以根据训练数据集自主学习相应的规律,以数据映射的方式建立水动力学特征预测模型,在实际应用中无需对流体运动控制方程进行求解,具有较高的计算效率.其中,卷积神经网络是近年来发展较快的机器学习算法之一,文献[9-11]的研究表明其可对线性、平面或空间数据分布信息进行提取,从而对于波浪时间序列、结构物形态等特征均具有较好的识别能力.

本文基于机器学习的理念,针对涵洞式直立堤的波浪透射问题搭建相应的卷积神经网络模型.文中通过CFD 计算模型生成相应的训练数据集,使卷积神经网络学习不同入射波、不同防波堤开孔条件下的波浪透射系数及透射波波形的变化规律.经过训练的卷积神经网络可建立相应的数据映射关系,通过接收新的工况条件作为输入参数,从而实现对透射系数及透射波形态的快速预测.

1 算法介绍

1.1 神经网络相关概念

人工神经网络是一种模仿生物体神经元之间信息传递及处理机制的数学模型,可接收多个不同的输入信号从而对相应的结果进行快速计算.大部分神经网络由多层神经元以首尾相接的方式组合而成,单个神经元的结构与功能如图1 所示.近年来,随着任务复杂度的提升,神经网络中的神经元数量和层数也大幅增加.对于此类模型,研究人员一般称之为深度神经网络.

图1 神经元的结构与功能Fig.1 Structure and function of the neuron

卷积神经网络一般指带有卷积运算的深度神经网络.常用的卷积运算有一维、二维以及三维等形式,此处根据文献[12]以二维卷积运算为例对其计算过程进行介绍.如图2 所示,卷积运算的过程可分为三步,第一步为构造卷积核并确定卷积核的系数;第二步为扫描整个源数值矩阵并将对相应位置的数值与卷积核的系数进行加权计算,第三步为将计算结果映射至另一新开辟矩阵中.一维、三维的卷积运算同理.卷积核的尺寸可根据不同的问题进行调整,本文中,二维卷积核选用3×3 矩阵,一维卷积核选用3×1 矩阵.

图2 卷积运算过程Fig.2 Convolution process

文献[13]指出经过卷积运算后的结果需要借助激活函数对其数值进行变换,使卷积神经网络获得对非线性规律的拟合能力.常用的激活函数有ReLU,Sigmoid,Tanh 等,本文中采用的激活函数为ReLU,其表达式为f(x)=max(x,0),即:对于卷积运算后的结果,小于0 的数值重置为0,大于0 的数值保持不变.该激活函数可使部分神经元的输出结果为0,减少神经元参数之间的互相依赖关系,从而获得较好的预测效果.单层卷积操作与激活函数的组合被称为卷积层,多个卷积层与神经元之间可以相互连接构成一个完整的卷积神经网络.相比于普通的神经网络,卷积神经网络可在不破坏原有数据分布规律的情况下提取一维、二维或三维数据的分布特征并从中获得相应的信息,具有更高的识别精度.

此外,根据文献[14],为了对数据特征进行降维,卷积神经网络一般会设置池化操作.池化一般有两种形式:最大池化和平均池化,最大池化采用区域内数值的最大值作为该区域的特征值,而平均池化采用该区域的平均值作为特征值,其区别如图3 所示.一维、三维的池化同理可得.相比于平均池化,最大池化可以更好地捕捉极值点的特征信息,是目前大部分卷积神经网络中常用的池化方式.

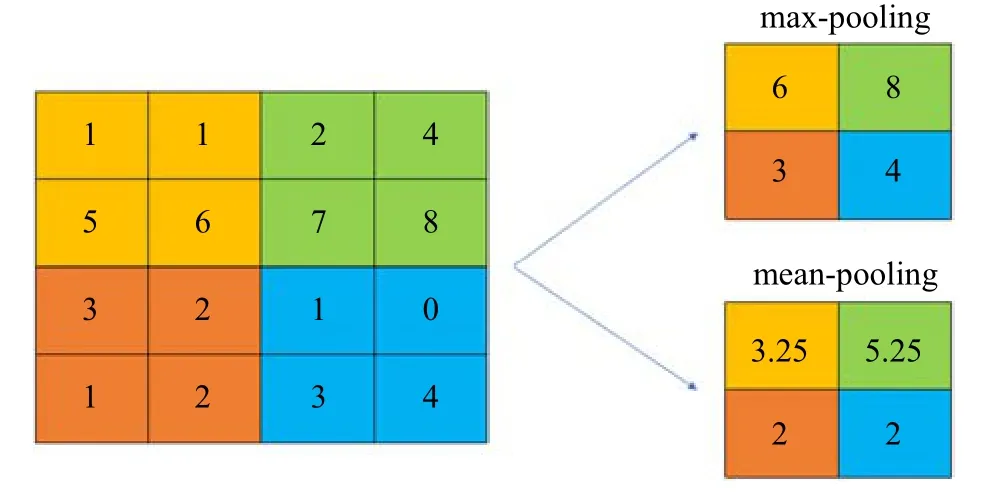
图3 池化运算方式Fig.3 Pooling operation

1.2 预测方式

文中卷积神经网络的输入参数为两部分,其一为入射波的波形,其二为固体结构物的形态,输入方式如图4 所示.对于波浪透射系数的预测,本文选取入射波的表达式如下

图4 卷积神经网络结构Fig.4 Structure of the convolutional neural network

式中T为可变的波浪周期,变化区间为[0.5 s,5 s],可用于训练卷积神经网络对于波浪周期信息的识别与提取能力;φ 为入射波的相位,其数值为[0,π]之间的随机数,可用于提升卷积神经网络的鲁棒性以及其对于波浪相位噪声的过滤能力.A为入射波的波高,本文中设为0.02 m,t为时间.此外,针对固体结构物的形态信息,本文采用数值标记的方式对其进行描述,即:固体所在的位置标记为1,其他位置标记为0.为保持两部分输入信息的量级接近,本文对入射波进行预处理,将所有入射波表达式除以波高A的数值.

对于透射波波形的预测,卷积神经网络可采用两种方式,第一种方式为先预测波浪透射系数,然后将其与入射波相乘;第二种方式为直接对透射波序列的形态进行预测.在第一种方式下,对于透射波波形的预测等同于波浪透射系数的预测,因此本文以第二种方式为例,测试卷积神经网络对于不同工况条件下透射波波浪形态的模拟能力.与预测波浪透射系数不同,透射波的波形与入射波相位及测点位置相关.考虑到不同相位的波形可在后处理中通过平移的方式进行变换,因此在预测时,本文中统一设置入射波以及透射波的初始相位为0.入射波的表达式如下

λ 为用于改变波高的随机系数,其数值位于区间[0.5,1.5]内,可用于训练卷积神经网络对于不同入射波波高的识别能力并将其特征反映至预测结果中.A为基准波高,其数值为0.02 m,t为时间,T为波浪周期,变化区间为[0.5 s,5 s].固体结构物的形态信息描述方式以及对于入射波的预处理同前文基本一致.

本文所采用的卷积神经网络结构如图4 所示,该结构采用一维的卷积算子提取入射波的特征信息,并采用二维的卷积算子提取结构物形态的特征信息.用于提取入射波信息的分支中,各卷积层所采用的卷积核数量依次为32,32,64,64,128,128;用于提取结构物形态信息的分支中,各卷积层所采用的卷积核数量依次为32,32,64,64,128,128,256,256.卷积层提取的特征信息经过全连接神经元的处理后,可得到波浪透射系数或透射波的形态.为了防止冗余信息干扰,该网络结构的形式为每两层卷积层后方设置一层池化层,选用的池化操作为最大池化.此外,全连接层中所采用的神经元数量为1024.

根据所求解问题的不同,本文设置了两种输出方式:当预测对象为波浪透射系数时,输出神经元的数量为1;当预测对象为透射波形态时,输出神经元的数量等同于波浪序列的长度.同时,文献[15-18]均指出设置随机断开层(drop-out layer)可以防止过拟合问题的出现并提升模型的预测精度,因此本文在全连接层与输出层之间设置了随机断开层,其主要思想是让隐藏层的节点在每次迭代时(包括正向和反向传播)有一定几率失效.它主要避免对某个节点的强依赖,让反向传播的修正值可以更加平衡地分布到各个参数上,从而防止过拟合.

1.3 训练数据集

文献[19-21]指出卷积神经网络的主要训练方式为:以输出端的结果与真实值之间的绝对误差作为训练指标,将训练过程转化为一个凸优化问题的求解过程,并通过相应的优化算法调整网络内部相应的系数使误差减小,从而使卷积神经网络的预测值尽可能地接近真实值.

卷积神经网络的训练精度与训练算法,学习率,训练轮数等超参数(hyper-parameter)直接相关.其中,训练算法和学习率主要影响训练过程的稳定性以及误差收敛的速度,训练轮数则主要影响训练过程的完整性.一般而言,随着训练轮数的增加,卷积神经网络的预测误差会不断下降,当误差收敛至基本不变时即可终止训练.

经过测试,本文对于卷积神经网络的训练参数设置如下:训练算法采用与文献[22]类似的Adam 算法,学习率为0.000 1,训练轮数为50,神经元随机断开比例为0.4,训练指标采用均方误差(mean squared error,MSE),即误差平方和的均值.此外,本文将分别采用40,80,120,160 组数据集用于卷积神经网络的训练,并对比不同的训练集数量对于预测精度的影响.

2 数据集介绍

2.1 数据集生成

本文所采用的训练数据集由基于紧致插值曲线CIP (constraint interpolation profile)算法的数值模型(CIP 模型)生成.该数值模型是一种具有较高计算精度的CFD 模型,文献[23-24]已将该算法应用于柱体绕流问题的求解,文献[25-26]将该算法应用于物体入水问题的求解,文献[27-29]将该算法应用于波浪与结构物相互作用问题的求解,并具有较为良好的表现.本文中共采用CIP 模型生成160 组工况用于卷积神经网络的训练,各工况的计算设置如下:数值水槽长度为26 m,水深0.4 m,模拟时长为25 s,时间步长为0.001 s.涵洞式防波堤位于水槽中间段,其形态如图5 所示,其长度为0.5 m,涵洞口径s的变化区间为[0.05 m,0.15 m],涵洞中轴线距水面高度d的变化区间为[0.15 m,0.3 m],入射波波浪周期T的变化区间为[0.5 s,5 s].造波方式为动量源项造波,造波位置附近以及堤后1.5 m 处分别设置测点用于监测入射波以及透射波的波高.此外,为避免反射波干扰模拟结果,水槽两侧设置了相应的消波区.

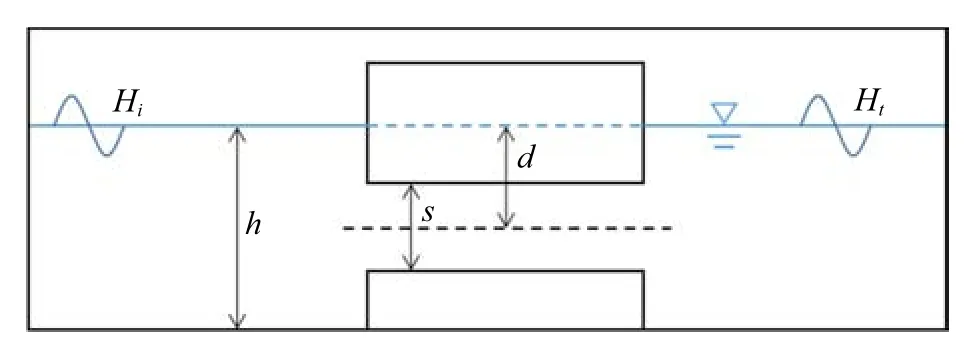
图5 涵洞式直立堤示意图Fig.5 Schematic diagram of culvert breakwater

2.2 数据集验证

文献[30]的研究结论指出卷积神经网络的学习和预测完全依赖于训练数据集,因此,数据集本身的准确性较为重要.本文采用新开展的实验结果对数值模拟结果进行验证.实验在浙江大学舟山校区港工馆内的断面水槽中进行,水槽长度为22 m,宽0.8 m,造波方式为推板造波.浪高仪的类型为电阻式浪高仪,精度为0.1 mm,其布置位置与数值模拟中的测点位置相同.实验的工况设置如表1 所示,共基于不同的组合生成27 组工况.为保障实验结果的准确性,每组工况均进行三次以上的重复性实验,并剔除异常值后取剩余数据的均值作为最终的实验结果.CIP模型计算结果与实验模拟结果的对比如图6 所示,横轴为实验结果,纵轴为数值模拟结果.由图可知,散点基本分布于斜对角线附近,表明CIP 模型所模拟的波浪透射系数与实验模拟的结果基本一致.该实验数据验证了CIP 模型计算结果的准确性,可知该模型可用于涵洞式直立堤的波浪透射问题的模拟,其生成的数据集较为可靠,能够用于卷积神经网络的训练.

表1 实验工况设置Table 1 Experimental condition setting

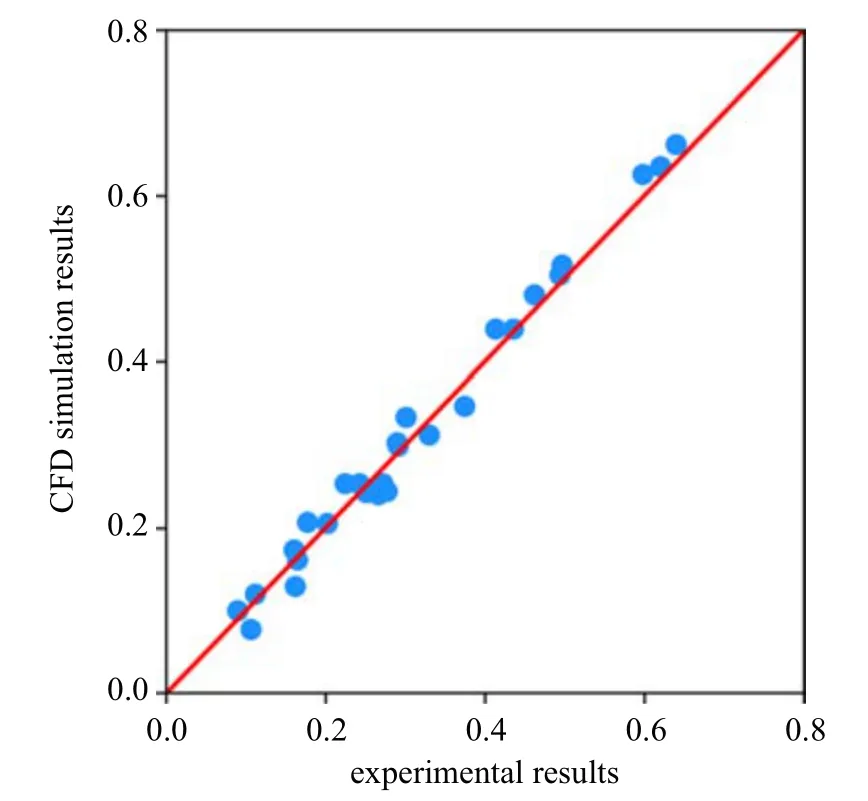
图6 波浪透射系数的数值模拟结果与实验结果对比Fig.6 Comparison between CFD results and experimental results of the wave transmission coefficient

3 预测结果及分析

如图7 所示,本文测试了不同训练集的数量对于卷积神经网络预测精度的影响.图中4 条曲线分别代表训练集数量为40,80,120,160 组时的验证集均方误差收敛曲线.验证集的作用为检验卷积神经网络模型是否存在过拟合的现象.此外,研究人员可通过观察卷积神经网络在验证集上的预测表现选取合适的训练参数,从而保障预测精度.本算例中,验证集的数量为20 组.由图可知,在训练的初期,模型的预测误差随着训练轮数的增加快速下降,而在中后期基本保持不变或呈现小幅度的震荡.卷积神经网络最终达到的预测精度与训练集的数量呈正相关,训练集数量为40 组时,模型的预测均方误差约为8.5×10−3,训练集数量为80 组时,预测误差减少至3.3×10−3.当训练集的数量增加至120 组时,其预测误差约为7.8×10−4,此时,卷积神经网络已达到较高的预测精度,当进一步增加训练集的数量至160 组时,预测误差基本保持不变.

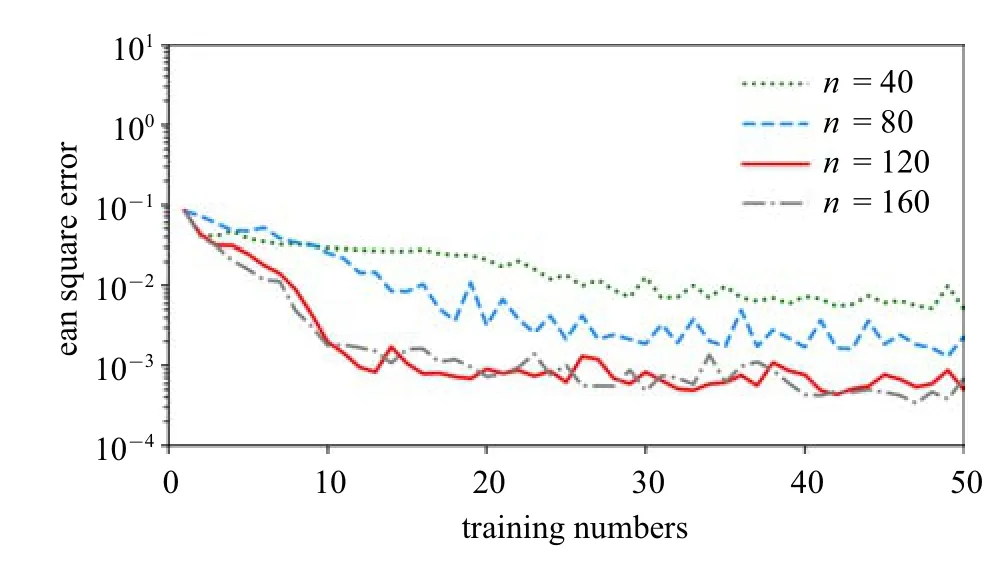
图7 不同训练数量所对应的均方误差Fig.7 Mean square error corresponding to different training numbers

图8 预测值与参考值的对比Fig.8 Comparison between predicted values and true values

图8 为基于不同数量的训练集所得到的模型在测试集上的预测表现.测试集的数量为30 组,与训练集和验证集相互独立,其作用为检验训练完毕的卷积神经网络模型在面对未知的输入数据时是否能够保持较好的预测能力.图中纵轴为卷积神经网络的预测值,横轴为相应的参考值.散点偏离红线的程度代表模型预测误差的大小,散点越接近红线,代表卷积神经网络的预测值越准确.由图可知,当训练集数量为40 组时,卷积神经网络初步具备对波浪透射系数的预测能力,但是误差较大;随着训练集数量的增加,散点逐渐向红线靠近,当训练集的数量增加至120 组时,其已达到较高的预测精度.进一步增加训练集至160 组时,散点的分布情况与训练集为120 组时的情况基本一致.由此可知,训练集的数量选为120 组较为合适.

此外,经过训练的卷积神经网络可保存相应的系数,实际应用中无需再次进行训练,可直接输入不同的工况条件对相应的波浪透射系数进行快速预测,具有较高的计算效率.本文所采用的CPU(中央处理器)型号为i7-6700k,GPU(图形处理器)型号为GTX Titan Black.经多次测试发现,卷积神经网络的训练时长与训练集的数量、学习率等参数相关,耗时一般为30 s 至200 s;而卷积神经网络的预测耗时与训练参数无关且较为稳定,计算波浪透射系数的平均耗时约为2.1 ms,在便捷性与计算效率上具有较为明显的优势.

图9 为不同入射波周期条件下所对应的波浪透射系数的变化情况,相应的涵洞孔径s为0.12m,涵洞中轴线至水面的距离d为0.24m.图中散点为卷积神经网络预测所得的结果,实线为CFD 数值模拟所得的结果.由图可知,卷积神经网络所预测的结果与CFD 数值模拟结果基本一致,较好地反映了透射系数随波浪周期的变化规律,具有较高的预测精度.

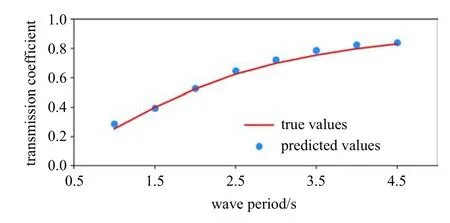
图9 透射系数随波浪周期的变化Fig.9 The change of transmission coefficient with wave periods

图10 为卷积神经网络对于波浪形态的预测结果以及相应的参考值,其训练参数、训练集数量与前文相同.图10(a)和10(b)分别为两个新工况条件下的透射波形态,图10(a)的波浪周期为1.612 s,涵洞孔径为0.052 7 m,涵洞中轴线距水面0.159 7 m,图10(b)的波浪周期为2.723 s,涵洞孔径为0.066 9 m,涵洞中轴线距水面0.192 2 m.图10(c)和10(d)分别为图10(a)和10(b)的局部细节图.如图所示,卷积神经网络能够对不同工况下的透射波形态进行预测,平均预测耗时约为4.7 ms.不同于传统数值模拟方式所得的结果,卷积神经网络的预测波形在波浪序列的前半段较为准确,从大约第6 s 开始逐渐出现较为明显的误差,该误差主要体现在以下两方面:

(1)卷积神经网络对于波高的预测值存在一定的误差,且波形并不严格满足规则波表达式.此外,由局部放大图可知,图10(d)对于波高的预测表现优于图10(c).导致该现象的原因在于,在训练过程中卷积神经网络以绝对误差作为训练指标,因此在实际预测时,较小的波高容易产生更大的相对误差;而在波高较大的情况下,卷积神经网络所预测的波形与真实波形更加相似.

(2)卷积神经网络预测的波浪周期与真实波形的周期之间存在少量误差,该误差会随着波浪序列长度的增加而累积.对此,考虑到透射波的波浪周期一般与入射波一致,可在实际的应用中基于入射波的周期信息对卷积神经网络的预测结果进行相应的修正.

图10 两种不同工况下的透射波形态结果对比Fig.10 Comparison of transmission wave shape under two different conditions

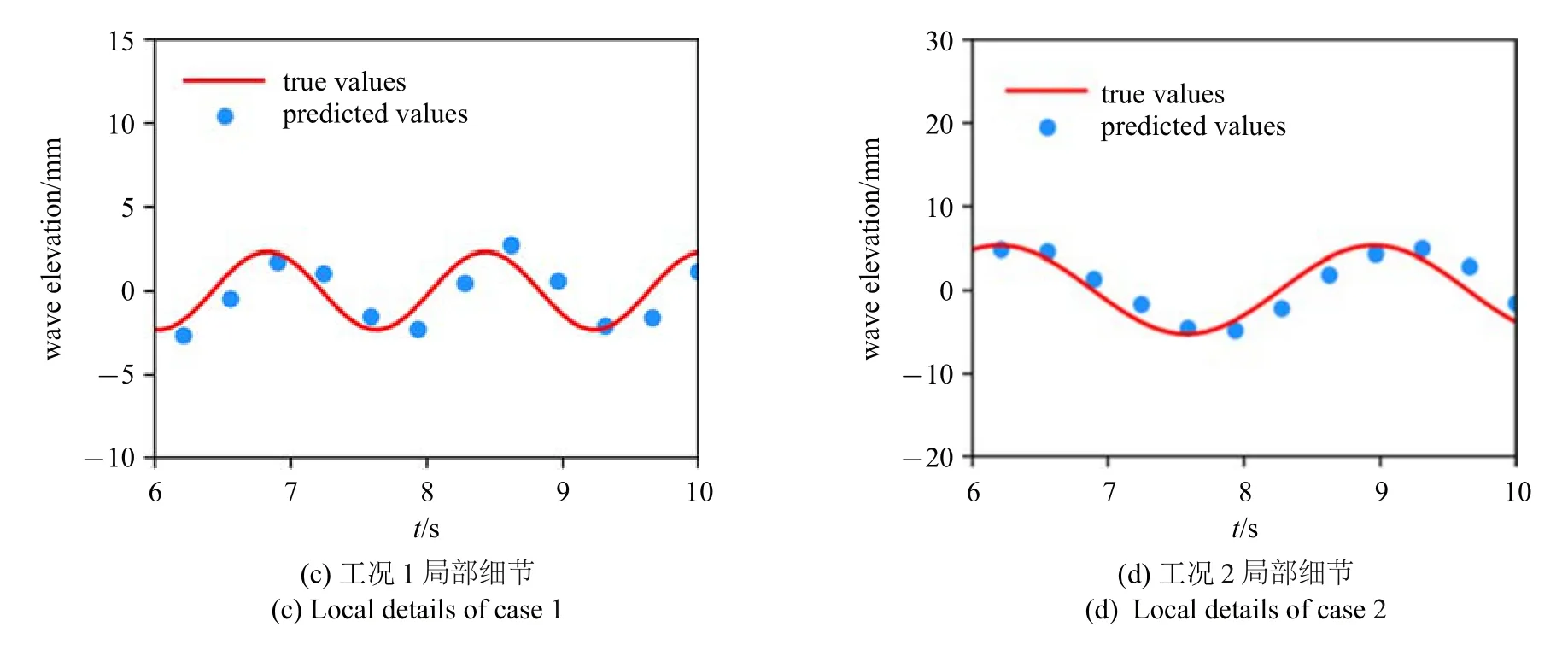
图10 两种不同工况下的透射波形态结果对比(续)Fig.10 Comparison of transmission wave shape under two different conditions(continued)

4 结论

本文针对涵洞式防波堤的波浪透射问题,采用卷积神经网络对其堤后透射系数以及透射波的形态进行了预测,可得到如下结论:

(1)经过训练的卷积神经网络可识别结构物形态与入射波特征,在短时间内对不同工况下的波浪透射系数及透射波的波形进行快速预测,其计算耗时在10 毫秒以内.此外,卷积神经网络的预测精度与训练集的数量呈正相关,在本文中,当训练集的数量大于120 组时,模型已具有较为理想的预测表现.

(2)在训练过程中,卷积神经网络一般以绝对误差作为训练指标,因此在预测较小的波高时容易产生更大的相对误差;而在波高较大的情况下,卷积神经网络所预测的波形与真实波形更加相似.

(3)对于透射波的形态进行预测时,卷积神经网络所得波形的周期与实际的波浪周期之间存在少量误差,该误差会随着波浪序列长度的增加而累积.因此,在实际应用时,可基于入射波的周期信息对卷积神经网络的预测结果进行相应的修正.

(4)卷积神经网络可为传统波浪透射问题提供新的求解理念,并可根据实际问题对不同类型的数据进行预测,在近海波浪实时预报等场景中的应用具有一定的可行性.