多层波导中矢量波动的时域人工边界条件1)

吴利华 赵 密 杜修力

(北京工业大学城市与工程安全减灾教育部重点实验室,北京 100124)

引言

用有限元法等数值方法分析大型结构的瞬态动力响应,一般的做法是引入人工边界,将结构−无限地基系统划分为有限域和无限域.无限域被截去,有限域用有限元法等数值方法模拟.为了消除波在人工边界上的虚假反射,需要在有限域的人工边界上施加人工边界条件(artificial boundary condition,ABC)来描述波动在无限域中的传播[1].ABC 是基于无限域的控制方程推导得到的.一般假定无限域是线性的,因为通常认为无限域中只存在向无穷远传播的波,不存在向有限域传播的波.

刚性基岩上卧成层土是一种普遍存在的地基形式,又称其为半开放的波导模型.与开放的半空间模型中只存在传向无穷远的行波相比,波导模型由于截止频率的存在,介质中同时存在截止频率以下的近场快衰波和截止频率以上的传向无穷远的行波[2-3].对于半空间模型,行波的振幅随着传播距离的增大快速减弱,所以即使不考虑介质材料阻尼的吸收效应,其无限域也可以被假定为小应变,即可以被假定为线性的.而对于波导模型,由于能量被困在介质中,行波的振幅衰减得较为缓慢,如果仅考虑几何散射不考虑介质吸收效应,将无限域假定为小应变是有问题的,所以更合理的做法应该是将波导模型考虑为有材料阻尼的线弹性介质.

本文的研究对象是具有确定尺寸参数的多层波导结构.Wang 等[4]研究表明,当多层波导内部结构尺寸存在随机缺陷时,弹性波会产生局部化现象.该现象使得在原本可以传播的频域范围内弹性波被禁止传播,进而多层波导结构中会产生不均匀的应力分布.鉴于问题的复杂性以及篇幅的限制,本文的研究范围不包括上述多层波导中随机失谐引起的弹性波局部化问题.

如有限域含有非线性等许多情况下,需要ABC是时域方法.相较于半空间模型的时域ABC 已有大量的研究工作[5-13],波导模型的时域ABC 研究工作较少.由于波导模型的ABC 需要能够同时模拟快衰波和行波的能量传递,直接在时域下建立其ABC 是有挑战的.根据是否精确地处理波导模型无限域定解问题,以下将已有的波导模型的ABC 分为精确的ABC 和近似的ABC 进行阐述.

精确的ABC 一般是首先基于解析法或半解析半离散法获得精确的频域动力刚度,再通过时域化方法建立时域ABC.解析法一般对单层介质标量波[14-16]适用,多层介质的解析解难以获得.半解析半离散法只对无限域的人工边界进行离散,对于单层介质和多层介质都适用,如边界元法(BEM)[17]、薄层法(TLM)[18-21]和比例边界有限元法(SBFEM)[3,22-26].BEM 需要基本解,而多层介质格林函数的基本解是复杂的,基本解的存在与否限制了BEM 在工程实际中的应用.相比于BEM,TLM 和SBFEM 不需要基本解,能够自动满足无穷远辐射边界条件.将频域动力刚度变换到时域,一种方法是时间卷积计算[3,25],该方法不仅耗时,而且不适用于非线性分析.学者们通过时间局部化方法建立了精确稳定的时间局部的ABC.Zhao 等[15]基于解析法获得2D 单层波导标量波的动力刚度,再用有理函数逼近方法建立精确的时域ABC.Prempramote 等[22]将解析法获得的动力刚度用双渐近连分式展开,建立了2D 单层标量波的时域ABC.Li 等[16]基于解析法获得2D 和3D 均匀层标量波的动力刚度,用动力刚度连分式展开的时间局部化方法建立了精确的时域ABC.Liu 等[26]基于半解析半离散法,利用算子分离法获得2D 单层标量波的时域ABC.Wang 等[23]基于SBFEM 和动力刚度的双渐近连分式展开[22]建立了2D 库水的时域ABC,并将方法嵌入到通用有限元软件ABAQUS 中用来计算坝−库水的动力相互作用.但是上述精确的时域ABC 都是针对单层波导标量波获得.根据作者的调查,目前几乎没有关于多层波导稳定的精确时域ABC 的相关报导.因为对于多层波导,其精确的时域ABC 易发生失稳,目前还没有较好地抑制其失稳的方法.

多层波导精确的时域ABC 难以获得,学者们通过对无限域定解问题作适量的简化,建立了多层波导近似的时域ABC.近似的低阶时空局部的ABC 由于其形式简单,在工程中被广泛使用,如黏性边界[5,27]、多次透射边界[7,11]以及黏弹性边界[9-10].这类低阶时空局部ABC 是基于半空间模型建立的,用于波导模型时精度较低.Hagstrom 等[28]建立了多层波导标量波的高阶时空局部ABC.完美匹配层法[29-30]是近年的研究热点,它是通过在人工边界外附加一层具有耗能作用的缓冲区来吸收透射波,但吸收层具有一定厚度,层厚度和耗能参数选择不当时,会导致精度低或发生失稳.Zhao 等[32]基于半解析半离散法和一种全频域收敛的动力刚度连分式展开构建了多层波导标量波的时域ABC,并对其稳定性进行了证明.吴利华等[33]将多层波导考虑为达朗贝尔黏弹性介质,利用和文献[32]类似的思路建立了考虑阻尼的多层波导标量波的时域ABC.高毅超等[34]将弹性动力学矢量方程强行解耦为两个标量波方程,基于SBFEM和双渐近连分式[22]构建了一种模拟单层波导矢量波的近似ABC.Liu 等[35]将文献[34]的方法嵌入到开源有限元软件OpenSees 中,分析了地下车站的地震动响应.Liu 等[31]基于半解析半离散法和算子分离法建立了多层波导矢量波的近似ABC,但该方法有时会出现失稳现象.就作者所知,目前几乎没有专门针对多层波导矢量波的稳定时域ABC 的相关研究.

本文的目标是建立多层波导矢量波稳定的时域ABC.借鉴文献[34]的做法将多层波导矢量波动方程强行解耦,得到x方向和y方向的两个标量波动方程.将文献[33]构建达朗贝尔黏弹性多层波导标量波的时域ABC 的思路用于解耦的x方向和y方向的两个标量波动方程,构建含有瑞利阻尼的线弹性多层波导矢量波的稳定的时域ABC.

1 问题描述

用有限元法分析如图1 所示的刚性基岩上卧成层地基上结构在动力载荷作用下平面内的时程响应.由于有限元法只能分析有限区域,需要引入人工边界将左右两个半无限域截去.为了避免波在人工边界处引起虚假反射,需要在有限域的人工边界处施加一个人工边界条件(ABC)来模拟波在无限域中的传播.

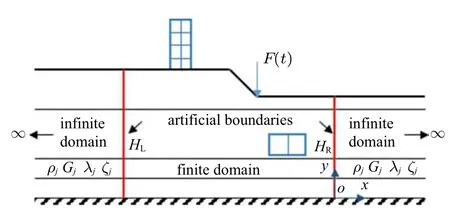
图1 刚性基岩上卧成层土Fig.1 A multilayered medium overlying rigid bedrock

有限域可以是非线性的,其有限元方程为

其中,下标b 和i 分别表示人工边界部分和有限域除了人工边界的其他部分,M是质量矩阵,C是阻尼矩阵,K是刚度矩阵,u是平面内位移向量,是非线性内力,b是体力,fi是施加在有限域的载荷,fb是施加在有限域人工边界上的力,即本文要建立的ABC,用来表示被截掉的无限域和有限域的相互作用.

一般认为无限域是线性的,若无限域包含非线性,需要对其进行等效线性化处理,使其满足线性条件.无限域的波动方程为

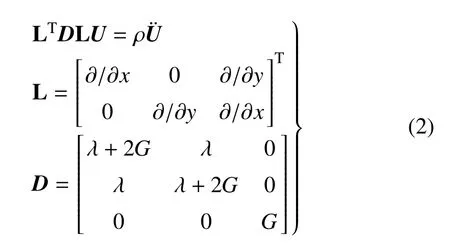
其中,变量上方的点表示对时间求导,(x,y)表示笛卡尔坐标,上标T 表示转置;U={ux uy}T,ux,uy分别为x方向和y方向的位移,ux和uy在不同土层的分界面以及人工边界处是连续的;ρ 是质量密度,λ 是拉梅常数,G是剪切模量,每一层的材料参数是常量,不同层的材料参数可不同.另外,无限域的上表面物理边界条件是应力为0,下表面物理边界条件是位移为0.土层的初始状态为静止.

2 时域人工边界条件

将无限域作为研究对象,建立时域吸收边界条件.文献[33]建立了模拟刚性基岩上卧多层介质中标量波传播的ABC,本文将该方法扩展到矢量波.方法的思路是:(1)将矢量波动方程简化为x方向和y方向解耦的两个标量波动方程;(2)基于比例边界有限元法,得到两个标量波动方程模态空间下半离散的频域动力刚度方程;(3)通过文献[33]中提出的连分式来表示频域动力刚度;(4)引入辅助变量,将连分式时域化,得到时域吸收边界条件;(5)所建立的ABC 可以和有限域的有限元方程无缝耦合,通过数值积分算法求解.

2.1 弹性波动方程简化

高毅超等[34]通过将矢量波动方程强行解耦,基于双渐近连分式建立了单层波导模型的ABC.本文借鉴其做法,忽略无限域波动方程(2)中x和y的耦合项,简化后得到关于x方向和y方向的两个标量方程分别为

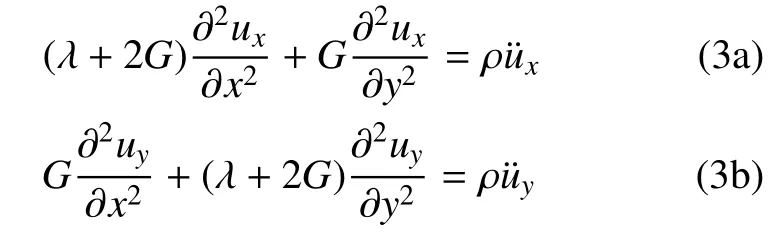
其中,x和y解耦简化处理后的应力−应变关系为

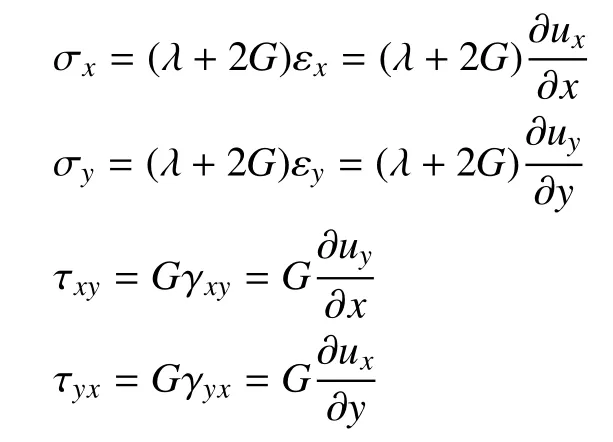
经过解耦简化处理后的上下表面物理边界条件分别为

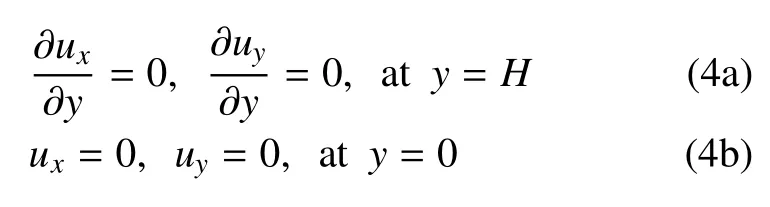
其中,H为半无限域的总层高.

2.2 模态空间下的频域动力刚度

根据比例边界有限元法(SBFEM)[23]建立模态空间下的频域动力刚度方程.

沿着土层y方向半离散简化处理后的无限域波动方程(3),同时考虑简化后的物理边界条件式(4)及介质交界面的连续条件,得到无限域简化弹性波动方程的比例边界有限元(SBFE)方程

基于简化后的本构关系得到无限域的人工边界上x和y方向的等效结点力分别为

引言的第二段阐述了波导模型应该考虑阻尼的吸收效应.由于瑞利阻尼是目前应用最广泛的阻尼矩阵的数值模型,本文假定无限域土层含有瑞利阻尼.瑞利阻尼定义阻尼矩阵是质量阵和刚度阵的线性组合[36],即CRayleigh=a0M+a1K,其中,ξ 为阵型阻尼比,ωi,ωj为选择用于确定阻尼系数a0和a1的频率点.瑞利阻尼的引入体现在式(5a)和式(5b)的第四项,需要说明的是,这里无限域瑞利阻尼的质量阵和刚度阵都是通过半离散x和y解耦的标量控制方程得到的,注意其与二维有限元法中的瑞利阻尼相区别.

为了使问题简单化,利用模态分解法[36],将物理空间下的SBFE 方程变换到模态空间.计算如下广义特征值问题

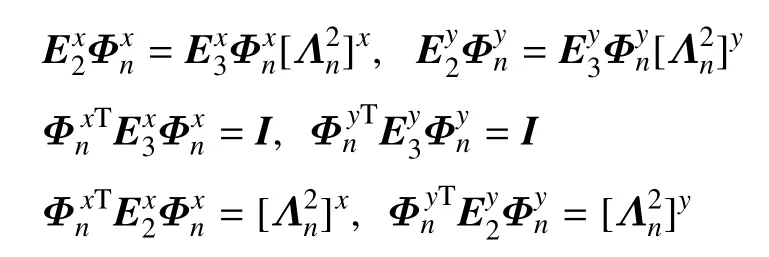
其中,上标−1 表示对矩阵求逆.

2.3 动力刚度的连分式展开

其中,z=iω/ωn,β=a0/ωn+a1ωn,i 是虚数单位,ω 表示圆频率.x和y方向分别有c=cp和c=cs.

由于x方向和y方向的SBFE 方程形式相同,以下仅给出x方向的推导过程,y方向的推导同x方向.以下推导思路类似文献[33],本文仅给出与文献[33]不同的地方以及相关重要公式,详细推导过程可参见文献[33].根据式(12)和式(13),无限域x方向模态空间的动力刚度可表示为如下的连分式

和文献[33]一样,连分式(14)也可用来近似地表示多层介质的动力刚度.对于多层介质,连分式中的通过求解如下黎卡提方程得到

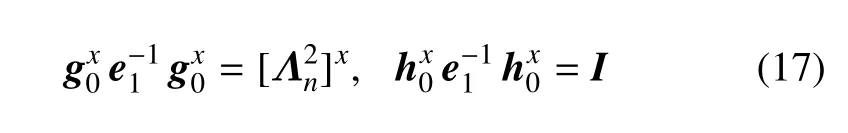
2.4 基于连分式的时域吸收边界条件

同文献[33]一样,通过引入辅助变量的方式将连分式时域化.将式(14)代入式(10a),同时引入辅助变量,得到

如今，微课的设计绝大多数都是对教材中知识点的教授，还滞留在对学生采取知识灌溉的方式上，然而微课的作用绝不止在于此。微课的时间很短，但是使用微课的最终目标是希望做到事半功倍，以小见大。所以，教师必须从简洁的授课型微课入手，渐渐向启发型、探究型的教学模式发展。想要做到这一点，教师在使用微课之前，就要做好充实的资料收集与课前准备，以便能够科学有效地权衡探究型活动和师生互动使用的微课时间。

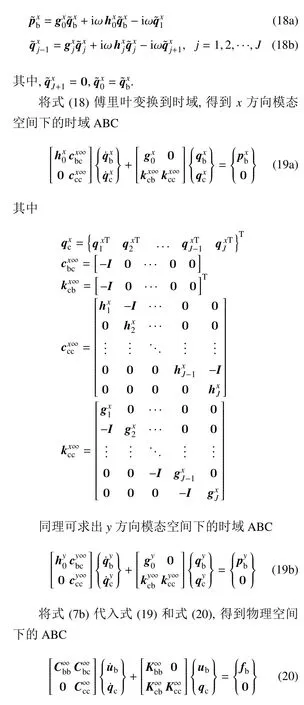
式(20)中,人工边界上单个结点的水平自由度和竖向自由度是空间解耦的,但是人工边界结点间的水平自由度和结点间的竖向自由度都是空间耦联的.其中

2.5 人工边界条件与有限元法耦合

本文建立的ABC 可与有限元法无缝耦合.将式(20)代入有限元方程式(1),得

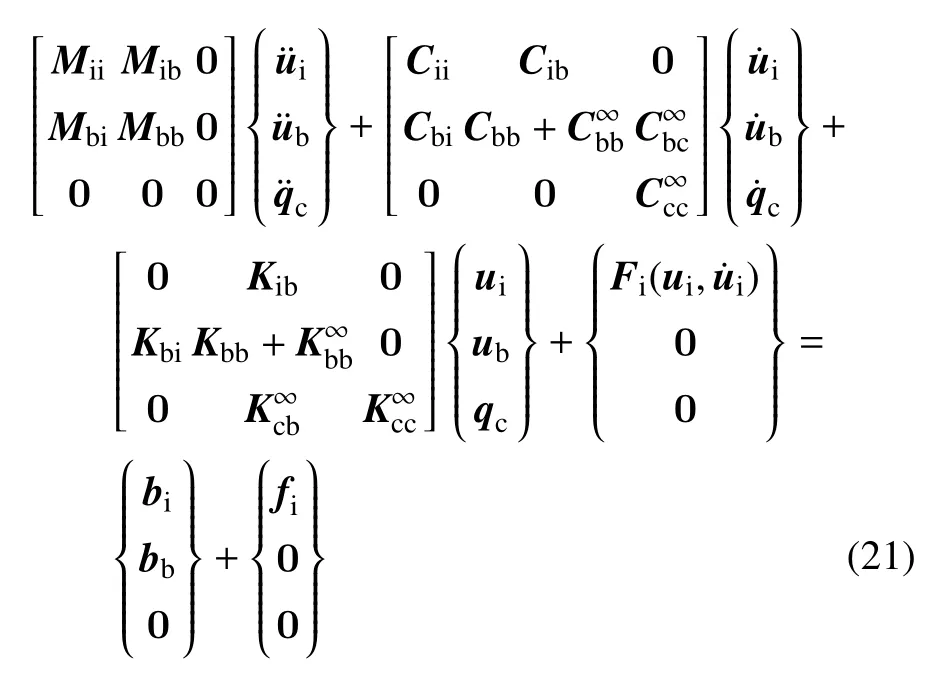
式(21)可通过标准的时间积分算法如Newmark 常平均加速度法等求解.

由于在有限域的人工边界上施加ABC 增加的额外自由度为

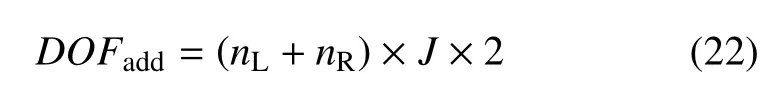
其中,nL和nR分别表示左无限域和右无限域参与计算的模态数.J表示连分式的阶数,通过算例分析统计,一般可取J=3,J的取值会在第3 节详细阐述.对于实际地震工程等问题,根据经验一般取模态数n≤3.所以额外增加的自由度数一般不会超过36,与有限域的自由度数相比,额外增加的自由度数几乎可以忽略不计.

本文建立的时域ABC 是对无限域矢量波动的近似模拟,为了实现高精度,需要将有限域的人工边界放置在距离兴趣域L处,L的取值将在第3 节通过数值算例详细分析.

本文的ABC 是基于全频域收敛稳定的连分式建立的,所以理论上ABC 应该是时域稳定的.方法的稳定性将在第3 节通过数值算例进一步说明.

3 方法的性能

本节通过数值算例说明方法的精度和稳定性.本文方法包含3 个可变参数:无限域的模态数n,连分式阶数J和人工边界远离兴趣域的距离L.文献[33]表明,仅用能被载荷激起的无限域的模态数n参与计算,不但能减少计算量,同时还不影响精度.下文详细分析J和L的取值要求.

分析如图2 所示的3 种模型.Model 1 和Model 2 都是自由场地,Model 1 的总层高H为20 m,Model 2 的总层高H为40 m.比较Model 1 和Model 2 的结果可以考察L,J取值与H的关系.Model 3 内含一个尺寸为5×5 的地下方洞,其总层高H为20 m.比较Model 1 和Model 3 的结果可以考察有无地下结构及地下结构尺寸对L,J取值的影响.3 种模型都是在地表作用10 m 长的水平线载荷,线载荷为狄拉克脉冲,其时程及频谱如图3 所示.为了考察狄拉克脉冲宽度是否会影响本文方法的精度和收敛性,考虑三种狄拉克脉冲:T=0.4,0.2 和0.1,其相应的频谱范围分别为0～10 Hz,0～20 Hz 和0～40 Hz.图2 中每个模型的兴趣域(region of interest,ROI)为蓝虚线框起来的部分,红实线表示人工边界,两条红实线框起来的部分是用于计算的有限域.L表示人工边界到兴趣域的距离.

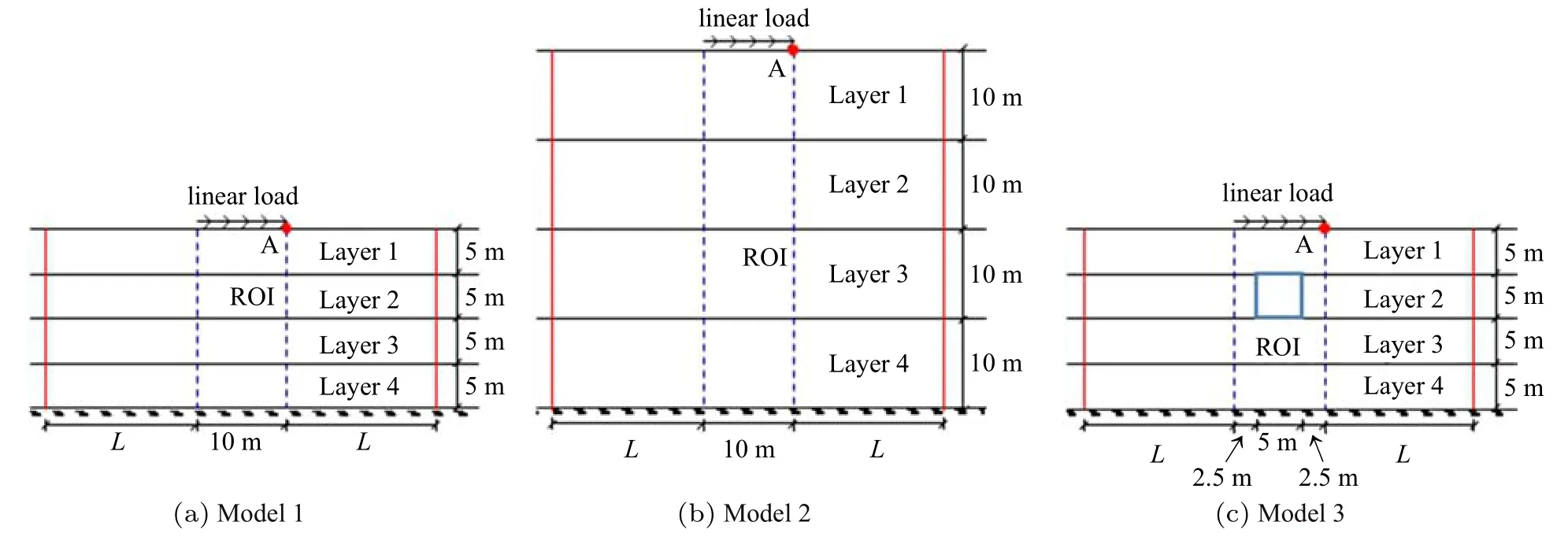
图2 数值算例模型Fig.2 Three models for numerical examples

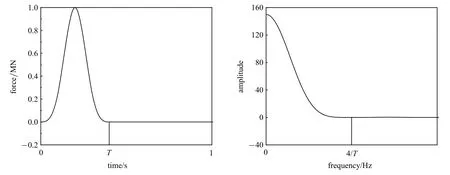
图3 狄拉克脉冲(T=0.4,0.2 和0.1)Fig.3 Dirac pulse(T=0.4,0.2 and 0.1)

为了分析土层材料参数对L,J取值的影响,将图2 中3 种模型分别都考虑为均匀介质和分别都考虑为4 层介质.分别将单层Model 1,单层Model 2 和单层Model 3 记为Case-1,Case-2 和Case-3;分别将4层Model 1,4 层Model 2 和4 层Model 3 记为Case-4,Case-5 和Case-6.Case-1～Case-6 土层都被考虑为有瑞利阻尼的线弹性介质,其土层材料参数见表1.6 种工况的计算时长都为2 s,输出A 点的水平位移时程和水平加速度时程.

用有限元法分析Case-1～Case-6.图2 所示的Model 1～Model 3 中两条红实线表示的人工边界框起来的部分为有限域,人工边界到兴趣域的距离被标记为L,在人工边界处施加ABC.有限域用四边形网格离散,Newmark 常平均加速度法用于时间积分计算.狄拉克脉冲中T=0.4 时,有限域的网格尺寸为2.5 m×2.5 m,时间步长为0.005 s.T=0.2 和0.1 时的网格尺寸和时间步长分别是T=0.4 时的0.5 倍和0.25 倍.

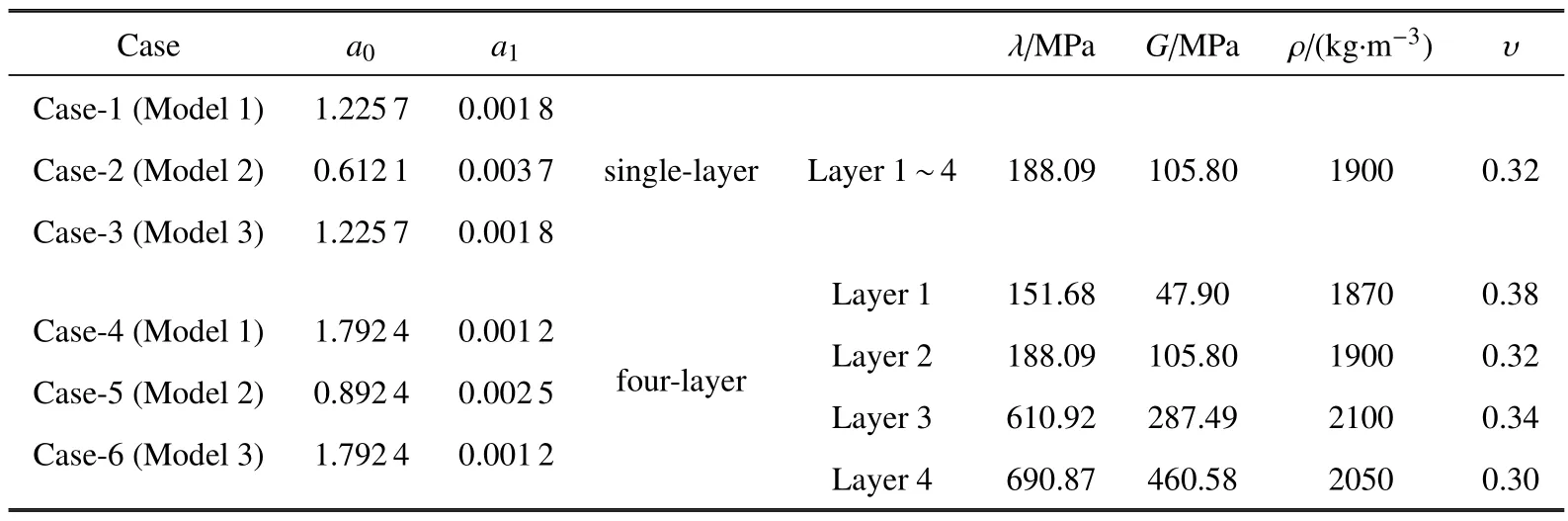
表1 Case-1～Case-6 的土层材料参数及其瑞利阻尼系数Table 1 Material parameters and Rayleigh damping coefficients of Case-1～Case-6

用于确定瑞利阻尼系数的频率点的选择方式有较多研究[37].本节的重点是验证本文提出方法的精度和稳定性,由于瑞利阻尼系数的具体数值不影响本文方法的性能,所以这里采用简单的频率点的选取方式,取土层前2 阶频率用于确定其瑞利阻尼系数a0和a1.Case-1～Case-6 土层的阻尼比ξ 都取为0.05,表1 列出了6 种工况的瑞利阻尼系数值.狄拉克脉冲中T=0.4 时,Case-1～Case-6 用于计算的无限域模态数n分别为2,3,2,1,3 和1.

将足够大有限域的有限元结果作为验证本文方法的参考解,大有限域尺寸的选取原则是人工边界上的虚假反射波在计算时间内不会污染兴趣域.

用数值算例结果分析J和L的取值对方法精度的影响.定义如下时程相对误差

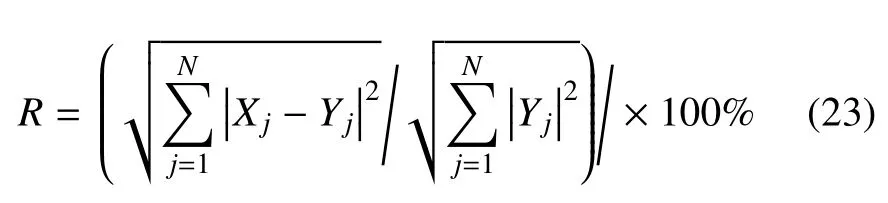
其中,Xj为基于有限元法和ABC 得到的小有限域的时程结果,Yj为仅基于有限元法得到的大有限域的时程结果(即参考解),N为总时步.

图4 展示了Case-1～Case-6 在连分式阶数J分别为1,2,3,4,5 的情况下,L=H～5H时对应的A点水平加速度时程的相对误差,这里狄拉克脉冲中T=0.4.为了说明本文方法的优越性,图4 也展示了同样L下黏性边界[5](VB)、刘晶波等[9]提出的黏弹性边界(VSB-Liu)和杜修力等[10]提出的黏弹性边界(VSB-Du)的结果.黏性边界和黏弹性边界都是经典的ABCs,因其形式简单且时域稳定,在工程中被广泛使用.黏性边界[5]是基于平面波假定建立的阻尼器边界条件,其每层的阻尼元件法向参数为CN=ρcp,切向参数为CT=ρcs.黏弹性边界是基于柱面波假定建立的并联弹簧−阻尼器边界条件.刘晶波等[9]提出的黏弹性边界每层的弹簧元件法向参数为KN=2G/r,切向参数为KT=3G/(2r),每层的阻尼元件法向参数为CN=ρcp,切向参数为CT=ρcs;杜修力等[10]提出的黏弹性边界每层的弹簧元件法向参数为KN=(λ+2G)/(3.6r),切向参数为KT=G/(3.6r),每层的阻尼元件法向参数为CN=1.1ρcp,切向参数为CT=1.1ρcs.3 个公式中每层的材料参数按实际值取,r认为是有限域的竖向对称轴到人工边界的水平距离.从图中可以看出,6 种工况呈现的结果规律类似.每种工况下,黏性边界和2 种黏弹性边界结果的相对误差接近,都远大于本文方法的结果.本文方法的J=1,2,3,4,5 对应的5 条曲线都是J=1 时相对误差较大,J=2 时相对误差快速变小,J=3,4 和5时三者的结果基本重合.根据大量算例结果(不仅限于图4 所列的算例结果)统计,当J>3 时,再增加J的值,基本不再改善精度.这是因为本文方法是一种近似方法,连分式只是近似地表示无限域的动力刚度,即使取很高的阶数,连分式也不能逼近无限域动力刚度的精确解.因近似损失的精度需要通过增大人工边界到兴趣域的距离L来弥补.为了减少可变因素,作者建议在使用本文方法时,参数J可以统一取为3.

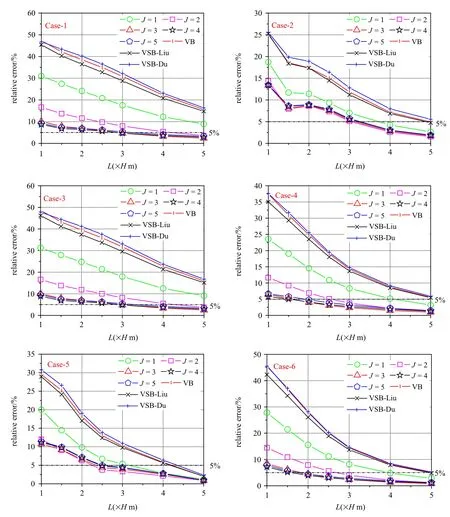
图4 6 种工况下基于本文方法、黏性边界(VB)和2 种黏弹性边界(VSB-Liu 和VSB-Du)的A 点水平加速度时程的相对误差Fig.4 Relative errors of time-history horizontal acceleration solutions at point A from the proposed method,the viscous boundary and two kinds of viscous-spring boundary VSB-Liu and VSB-Du for Case-1～Case-6

进一步详细分析L的选取原则.分别计算Case-1～Case-6,当J=3,L为H～5H时A点水平位移时程和水平加速度时程各自的相对误差,这里狄拉克脉冲中T=0.4.将相对误差≤5%时各自对应的L值,以及同样L下黏性边界和黏弹性边界结果的相对误差列于表2.根据表2 可以得出以下结论(表中第2 列u表示位移,a表示加速度;第3 列表头L表示人工边界到兴趣域的距离;第4 列表头ABC 表示本文方法的结果;第5 列表头VB 表示黏性边界[5]的结果;第6 列表头VSB-Liu 表示刘晶波等[9]提出的黏弹性边界的结果;第7 列表头VSB-Du 表示杜修力等[10]提出的黏弹性边界的结果).

(1)对比表2 的最后3 列可以看出,黏性边界和黏弹性边界结果的相对误差接近,都约为本文方法结果的5～6 倍左右,除了Case-2 和Case-5 的加速度时程结果,其黏性边界和黏弹性边界结果的相对误差是本文方法结果的2～3 倍.另外,本文方法与黏性边界和黏弹性边界相比,仅多出少量的辅助自由度数,对于Case-1～Case-6,其值分别为24,36,24,12,36,12.因此本文方法相比于黏性边界和黏弹性边界,能够在几乎不增加计算量的情况下使精度提高约2～6倍.精度的提高程度与土层的总厚度有关,原因是本文方法是针对层模型建立的,其应用在深厚土层和浅土层都具有高精度;黏性边界和黏弹性边界是针对半空间模型建立的,由于深厚土层相较于浅土层更接近半空间模型,因此其在深厚土层中要比在浅土层中的精度高.

(2)对比表2 第3 列表示的水平位移对应的L值和水平加速度对应的L值可以看出,每种工况下,水平加速度对应的L值都是水平位移对应结果的2 倍,除了Case-5 是2.5 倍.说明人工边界的位置以加速度为控制指标来确定更为严格.

(3)比较单层的Case-1 和Case-3 水平加速度对应的L值.Case-1 和Case-3 总层高相同,Case-1 为自由场地,Case-3 含有5 m×5 m 的地下结构.两者都是L=3H时,水平加速度时程的相对误差能控制在5%以内.说明L的取值基本不受是否含有地下结构或结构尺寸影响.比较4 层的Case-4 和Case-6 能得出同样的结论.

(4)比较单层Case-1 和Case-2 水平加速度对应的L值.Case-1 和Case-2 都是自由场地,Case-2 的总层高H是Case-1 的2 倍.两者都是L=3H时,水平加速度时程的相对误差能控制在5%以内.同样,比较4 层的Case-4 和Case-5.为了将水平加速度时程的相对误差控制在5%以内,Case-4 要求L=2H,Case-5要求L=2.5H.说明L的取值大约与土层总层高H成正比关系,关系系数与土层的材料参数有关.根据大量算例统计,一般L=3H都能将加速度时程相对误差控制在5%以内.

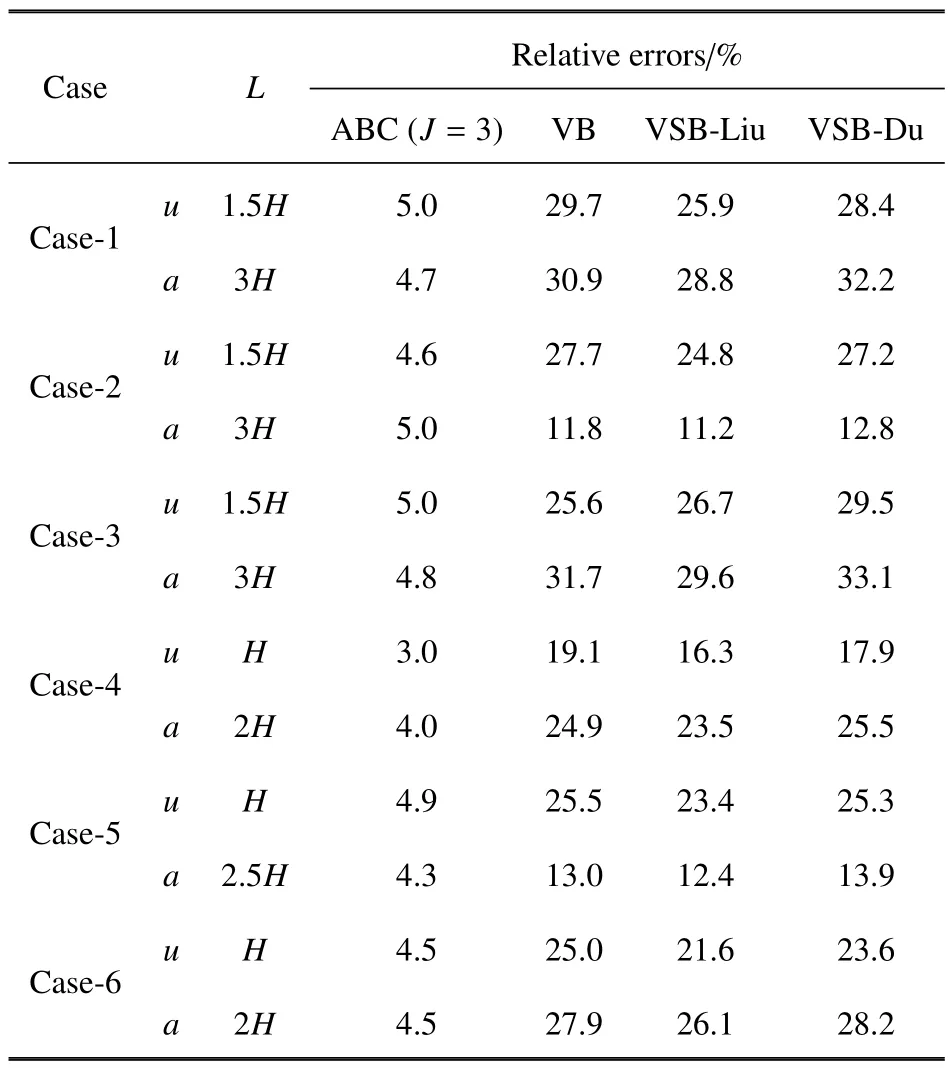
表2 本文方法的A 点水平位移时程和水平加速度时程各自的相对误差≤5%时对应的L 值,以及同样L 下黏性边界和2 种黏弹性边界结果的相对误差Table 2 Values of L when relative errors of horizontal displacement and of horizontal acceleration at point A from the proposed method not greater than 5%,and relative errors of those solutions from the viscous boundary and two kinds of viscous-spring boundary under the same value of L

图5 展示了本文方法的计算结果满足工程精度要求(相对误差≤5%)时的A点水平加速度时程.其中,J=3,Case-1～Case-6 对应的L值分别为3H,3H,3H,2H,2.5H,2H.同样L下刘晶波等提出的黏弹性边界(VSB-Liu)的结果也被展示在图5 中.从图中可以看出,本文方法的结果和参考解几乎完全吻合,而黏弹性边界基本是在0.5 s 之后结果的精度较低.

为了研究图3 中狄拉克脉冲的宽度对本文方法的计算精度和收敛性的影响,图6 展示了Case-6 在T=0.2 和T=0.1 两种载荷下,本文方法(J=1～5,L=H～5H)和VSB-Liu 方法的计算结果,图中纵坐标为式(23)所示的A点水平加速度时程的相对误差.T=0.2 时,本文方法中模态数n取为5;T=0.1时,n取为10.可以看出,图6(a)(T=0.2)和图6(b)(T=0.1)中结果的规律和图4 (T=0.4)中Case-6结果的规律相似,都是黏弹性边界结果远大于本文方法的结果,本文方法J=3 时结果已收敛,再增大J值,基本不再改善精度;因近似损失的精度需要通过增大人工边界到兴趣域的距离L来弥补,都是当L=2H时,能满足工程精度要求(相对误差<5%),随着L的增大,结果向0 收敛.因此,图3 中狄拉克脉冲的宽度基本不会影响本文方法的计算精度和收敛性.

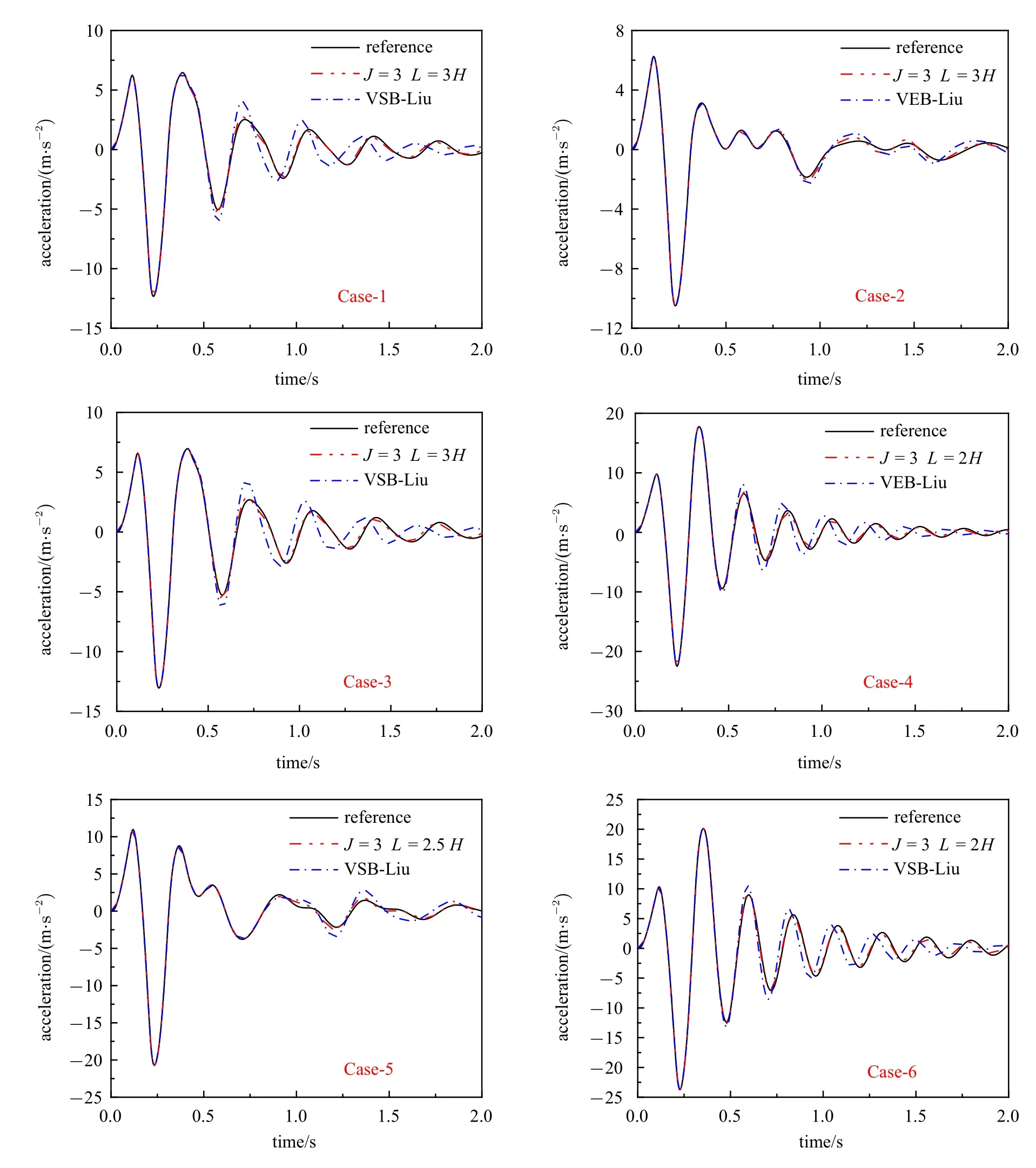
图5 本文方法(J=3,Case-1～Case-6 对应的L 值分别为3H,3H,3H,2H,2.5H,2H)的A 点水平加速度时程结果以及同样L 下黏弹性边界的结果Fig.5 Time histories of horizontal acceleration at point A from the proposed method(J=3 and L=3H,3H,3H,2H,2.5H,2H for Case-1～Case-6,respectively)and from the viscous-spring boundary

图6 T=0.2 和T=0.1 两种狄拉克脉冲下,本文方法(J=1～5,L= H～5H)和VSB-Liu 方法的计算结果Fig.6 Results from the proposed method(J=1～5,L= H～5H)and from the VSB-Liu method under two kinds of Dirac pulse with T=0.2 and 0.1

由于本文的ABC 是基于全频域收敛的连分式建立的,理论上ABC 应该是时域稳定的.通过后验的方法进一步验证本文方法的稳定性.根据线性系统理论,若ABC 系统的特征值全部分布在复平面左侧,则说明ABC 稳定.图7 展示了Case-1～Case-6 的水平方向上和竖直方向上式(19)所示的模态空间下的ABC 系统的特征值在复平面的分布.总特征值的个数为n×(J+1).从图中可以看出ABC 特征值的实部都小于0,且其分布规律为:特征值分布在一系列半圆上,且半圆的数目是模态数n,每个半圆上特征值的数目是J+1.由于本算例每一个虚部为0 的特征值都是重根,因此图中呈现出来的是每个半圆上特征值的数目为J.

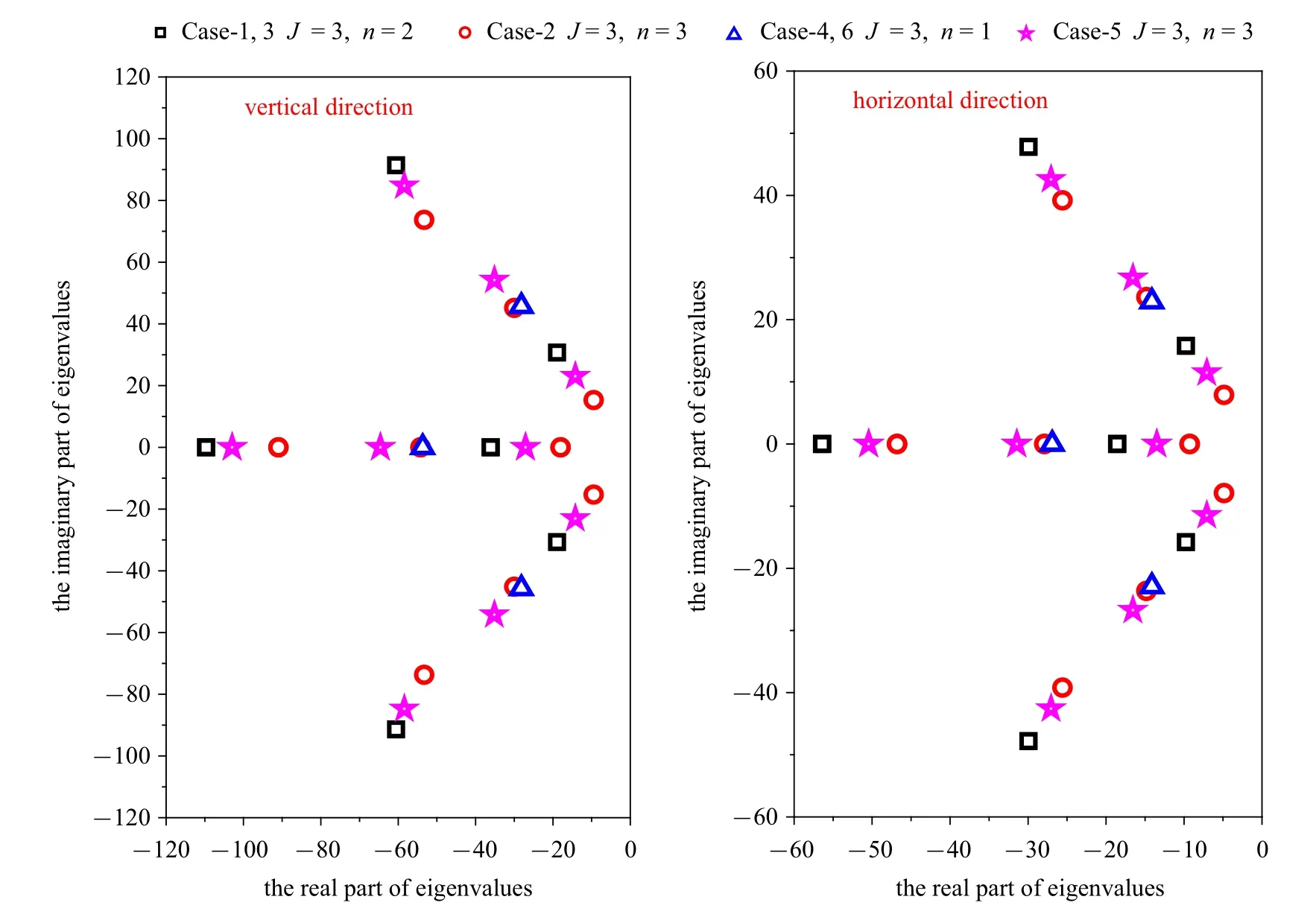
图7 Case-1～Case-6 的水平方向上和竖直方向上模态空间下ABC 系统的特征值在复平面的分布Fig.7 Distribution of eigenvalues in complex plane of ABC system in the horizontal and the vertical directions in the modal space for Case-1～Case-6

4 结论

本文将文献[33]中针对标量波提出的方法扩展到矢量波,建立了一种稳定的近似时域人工边界条件(ABC)来模拟含有瑞利阻尼的线弹性多层波导模型的平面内矢量波动.相较于文献[33]的方法只能模拟标量波问题,本文提出的方法不仅适用于矢量波问题,对标量波问题也同样适用.

提出的方法中影响计算精度和计算效率的参数有3 个,分别为无限域的模态数n,连分式阶数J,和人工边界远离兴趣域的距离L.数值算例表明,仅用能被载荷激起的无限域的模态数n参与计算即可.由于本文方法是一种近似方法,一般当J>3 时,再增大J值,基本不再改善精度.作者建议使用本文方法时参数J可以统一取为3.因近似处理损失的精度需要通过增大人工边界到兴趣域的距离L来弥补.确定人工边界位置L以加速度为分析指标更为严格.L的取值基本与地下结构尺寸无关,它与土层的总层高H约成正比关系,关系系数与土层的材料参数有关.一般取L=3H都能将加速度时程相对误差控制在5%以内.本文数值算例结果表明在同样的L下,与工程中被广泛使用的黏性边界和黏弹性边界相比,本文方法能够在几乎不增加计算量的情况下一般大约能使精度提高2～6 倍,精度的提高程度与土层的总厚度有关.

本文提出的ABC 在理论上是稳定的,数值算例也进一步验证了其稳定性.算例表明模态空间下ABC 系统的特征值呈一定规律分布在复平面的左侧,其分布规律为:特征值分布在一系列半圆上,半圆的数目是模态数n,每个半圆上特征值的数目是J+1.

本文提出的ABC 虽然人工边界上单个结点的水平自由度和竖向自由度是空间解耦的,但是人工边界结点间的水平自由度和结点间的竖向自由度都是空间耦联的.下一步工作可以考虑将方法进一步优化,使人工边界上结点间的水平自由度和结点间的竖向自由度都空间解耦,更方便工程应用.另外,可以考虑借鉴本文方法的研究思路建立矢量弹性波精确的时域人工边界条件.