基于雨燕翅膀的仿生三角翼气动特性计算研究1)

张 庆 叶正寅

∗(西安航空学院飞行器学院,西安 710077)

†(南洋理工大学机械与航空工程学院,新加坡 639798)

∗∗(西北工业大学航空学院,西安 710072)

引言

自20 世纪90 年代开始,微型飞行器(micro aerial vehicle,MAV)一直是新型飞行器设计领域内的前沿方向和研究热点[1-3].近十年来,随着微机电系统加工制造技术的进步以及消费级微型无人机的广泛需求,MAV 更是引起了航空领域内的极大关注.一般来说,MAV 的尺寸小于15 cm,起飞总重小于200 g,飞行速度约为10 m/s[4].因为它的尺寸小,质量小,所以可以更方便地去执行一些常规尺寸飞行器难以完成的特殊任务[4-6].但是,由于尺寸小,飞行速度低,MAV 的飞行雷诺数很低(101～103),由此带来了一系列的低雷诺数气动问题,这时常规飞行器(雷诺数在106以上)气动设计的原理和方法已经不再适用[4].比如,固定翼MAV 翼面的气流很容易发生分离,导致气动效率和操纵效率急剧下降,因而航程、航时以及飞行稳定性显著降低.研究表明,雷诺数在106～107时,光滑翼最大升阻比的量级是102～103,而雷诺数在104以下时,其最大升阻比的量级在100以下[4].此外,由于飞行速度较低,MAV 很容易受到环境中的阵风和大气湍流的影响,从而造成操纵特性和飞行稳定性的显著下降[7].

由于低雷诺数流动的特点,目前将客机或战斗机机翼气动构型直接缩比设计出来的MAV 的气动效率较低,当前MAV 的进一步发展和应用遇到了新的技术瓶颈[4-5].为了提高MAV 的气动性能和飞行稳定性,必须开展新型气动布局的研究,以探索更加适合未来MAV 的气动构型形式.

自然界众多动物具有优异的飞行能力,这与它们的可根据飞行状态进行自适应的翅膀息息相关.以雨燕为例,它一生中大部分时间都与翅膀有关,如觅食、求偶、迁徙、栖息等活动[8-13].雨燕的翅膀在滑翔时呈后掠镰刀状,水洞实验研究证实这种构型会在翅膀表面产生出稳定的前缘涡,从而产生稳定的涡升力[10-15].这与三角翼布局战斗机的前缘涡升力类似[16-24].但是,研究表明,雨燕翅膀的臂翼段的前缘是光滑的,而手翼段的前缘是尖的.光滑前缘产生附着流动,而尖前缘会产生分离流动,从而带来附加涡升力[10].针对简单的后掠三角翼,已有众多文献研究过前缘形状对涡流发展特性和总体气动性能的影响规律[25-28].文献[25]对50◦后掠三角翼的风洞实验结果证明,前缘斜切对气动特性有显著影响,迎风面斜切可以显著提升失速前的升力,而背风面斜切可以显著提高失速迎角和最大升阻比.文献[26]的水洞试验结果也证实,在低雷诺数流动条件下,三角翼气动特性与前缘涡的演化密切相关.

考虑到雨燕的手翼会通过羽毛改变前缘外形以适应不同的飞行状态,由于前缘涡的发展和演化与众多物理因素有关[10-12],目前对仿生三角翼前缘变形带来的涡流特性改变以及气动效应变化还未有明确结论[27-28].为了定量探讨前缘形状对仿生布局涡流结构和气动特性的影响,本文以类似雨燕翅膀的中等后掠三角翼为研究对象,采用数值模拟方法,研究了低雷诺数流动条件下具有不同前缘钝度的仿雨燕三角翼的涡流演化性态和总体气动性能变化情况,明确了不同雷诺数时前缘形状对涡流强度和涡破裂位置的影响规律.在当前大力发展新型微型飞行器的时代背景下,希望本文的探索性研究能为未来微型仿生飞行器的设计和制造提供一定的理论基础和技术支撑.

1 几何模型、计算方法以及算例验证

爱丁堡大学Viola 团队对前缘斜切角60◦的普通三角翼和仿雨燕三角翼进行了水洞实验研究,采用粒子成像测速法(particle image velocimetry,PIV)技术观测了两种翼的涡流结构,结果证实,仿雨燕三角翼后缘几何外形收缩对于前缘涡结构没有明显影响[9].作者指出,三角翼的涡流结构可能与前缘外形有关,为了厘清此问题,本文在Viola 研究基础之上,设计了具有不同前缘斜切角的普通三角翼和仿雨燕三角翼模型,然后对这些模型在与雨燕滑翔飞行类似的流动条件下的涡流结构和气动特性进行数值仿真,以探索三角翼布局的涡流发展特性和总体气动特性.

本文的普通三角翼和仿生三角翼与Viola 水洞实验所用模型完全一致,另外,由于实验模型的前缘斜切角β 为60◦,为了研究前缘形状对涡流特性的影响规律,增加了前缘没有斜切以及斜切角30◦的两种情况,因此,普通三角翼和仿生三角翼均有β=0◦,β=30◦,β=60◦三种前缘外形.图1 是两种三角翼模型几何参数的定义(β=30◦),两个翼的前缘点和后缘点沿着弦向的距离均为l=0.15 m,展长均为b=0.25 m,厚度为t=0.01 m,前缘后掠角均为Λ=50◦,仿雨燕式的三角翼的上翼面翼根弦长为Cr=0.065 m.升力/阻力系数的参考面积取各自的投影面积,分别为0.018 75 m2和0.008 125 m2.自由来流风速V∞=1.538 6 m/s,压力为101 325 Pa,迎角α 变化范围为0◦～20◦,计算间隔为2◦,基于前后缘弦向距离l的雷诺数Re=1.58×104.

图1 三角翼布局几何参数Fig.1 Geometric parameters for delta wings

本文数值模拟的重点在于验证计算方法对低雷诺数流动的气动力计算以及对三角翼涡流流动细节结构的捕捉能力,考虑到计算工具的鲁棒性,选择商业软件ANSYS Fluent 19.5 作为本文的流场模拟工具,所有的计算工作在新加坡南洋理工大学高性能计算中心Gekko 集群上完成.前期的研究结果证明,S-A湍流模型可以比较精确地捕捉三角翼表面的涡流结构,因此本文流场求解部分采用基于S-A 湍流模型的有限体积法[29-31],计算网格采用结构化网格,不同区域的网格分布情况详见图2.远场为长方体,流向X、展向Y和法向Z的尺寸分别为40b,40b,200t.对于普通三角翼,上下表面采用单块Y 形网格分布,对于仿生三角翼,上下表面采用左右侧对称的两块Y形网格分布,如图2(b)所示.附面层第一层高度为1.661×10−4m(相应的y+=1.0),如图2(c)所示.如图2(a)所示,长方体远场的左侧边界为速度入口,右侧边界为压力出口,下侧和前后侧边界为速度入口,而上侧边界在迎角为0◦时是速度入口,而在迎角为正时是压力出口边界.此外,需要说明的是,在低雷诺数流动条件下左右两侧涡流相互干扰作用很微弱,整个流场关于Y=0 平面是完全对称的,本文所有流场仿真都是定常结果.

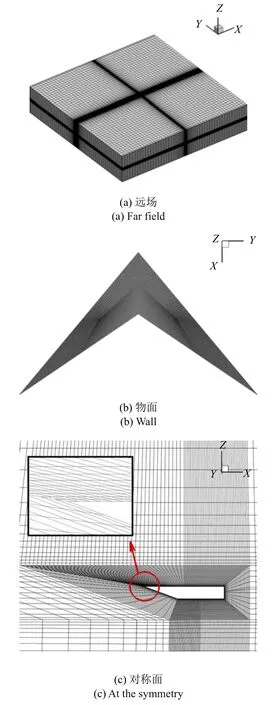
图2 不同位置的网格分布情况Fig.2 Computational grid distribution at different positions

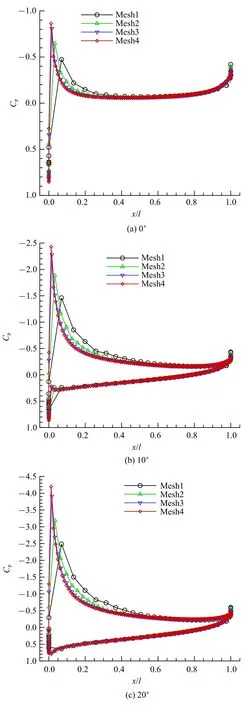
图3 迎角为0◦,10◦,20◦时对称面压力系数对比Fig.3 Comparison of pressure coefficients at symmetry at angle of attack 0◦,10◦,20◦

高质量的网格是精确数值模拟的前提,为了验证本文计算方法的网格无关性,首先采用由疏到密的四套网格分别计算了普通三角翼(β=0◦)在迎角为0◦,10◦和20◦时机翼表面对称面处的压力系数分布情况,详细结果如图3 所示.四套网格由疏到密,物面三角形每条边的节点数分别为29,61,121,161,相应的流体域六面体网格单元总数分别为248 000,1 008 000,3 492 000,5 136 000.由图可知,网格越密,计算结果越精确.在对比的三个迎角下,第三套网格的模拟结果和第四套网格模拟结果几乎完全重合,说明继续加密网格对计算精度没有明显的提高作用,因此,本文以下所有的网格尺度和规模都与第三套网格类似.

2 数值模拟结果及分析

为了厘清前缘削尖角度和收缩后缘对低雷诺数三角翼涡流结构和总体气动性能的影响规律,本节从气动力系数和涡流演化结构两个方面来定量探究这些特性.

2.1 气动特性

图4 分别是不同迎角时六个模型的升力系数CL、阻力系数CD以及升阻比K的对比图,需要注意的是,所有图中“Swift”代表仿雨燕式后缘收缩的三角翼,而“Delta”代表普通三角翼.从图4(a)可以看出,在前缘没有斜切时,普通三角翼和仿雨燕三角翼的升力系数变化趋势类似,都是随迎角增大而增大,在0◦迎角时由于对称性,两者的升力均为0,迎角继续增大,仿雨燕翼的升力比普通三角翼稍低,10◦迎角时仿雨燕翼的升力比普通三角翼低6%,20◦时低3%.虽然两种翼在前缘没有斜切时升力系数变化规律类似,但是,前缘斜切以后两种翼呈现出完全相反的升力变化趋势.从图4(a)中可以看出,对于普通三角翼,斜切角越大,相应的升力越小,迎角越大,升力减小越严重.对于斜切角30◦的模型,10◦迎角时的升力比无斜切模型低9%,而20◦时低23%.而对于斜切角60◦的模型,10◦迎角时的升力比无斜切模型低15%,而20◦时低31%.相反,对于仿雨燕三角翼,斜切角越大,相应的升力越大(迎角小于18◦时),迎角越小,升力增大越明显.对于斜切角30◦的模型,10◦迎角时的升力比无斜切模型高14%.而对于斜切角60◦的模型,10◦迎角时的升力比无斜切模型高28%.迎角为18◦时,三个模型升力系数接近,而迎角为20◦时,无斜切模型的升力系数稍大于有斜切的两个模型.值得注意的是,迎角为0◦时,对于仿雨燕翼,前缘斜切产生了较大的正升力,而对于普通三角翼,前缘斜切产生了较小的负升力.

从图4(b)可以看出,在前缘没有斜切时,普通三角翼和仿雨燕三角翼的阻力系数变化趋势类似,都是随迎角增大而增大,但是,仿雨燕翼的阻力比普通三角翼大得多,0◦迎角时仿雨燕翼的阻力比普通三角翼大108%,10◦,20◦时分别为65%,37%.从前缘斜切效果来看,对于普通三角翼,前缘斜切使阻力减小,斜切角越大,阻力减小效果越明显.迎角越小,阻力减小效果越明显.对于斜切角30◦的模型,0◦,20◦迎角时的阻力比无斜切模型分别降低10%,2%.而于斜切角60◦的模型,0◦,20◦迎角时的阻力比无斜切模型分别降低33%,16%.对于仿雨燕三角翼,斜切角为60◦时,0◦,20◦迎角时的阻力比无斜切模型分别降低35%,3%,这与普通三角翼类似.而斜切角为30◦时,迎角小于8◦时,斜切模型的阻力系数比无斜切模型小,而迎角大于8◦时,斜切模型的阻力系数比无斜切模型大.0◦迎角时的阻力比无斜切模型小11%,而8◦,20◦迎角时的阻力分别比无斜切模型大2%,6%.

从图4(c)可以看出,在前缘没有斜切时,普通三角翼和仿雨燕三角翼的升阻比变化趋势类似,都是随迎角增大而增大,但是,由于仿雨燕翼的阻力系数远大于普通三角翼,因此仿雨燕翼的升阻比远小于普通三角翼,在0◦,10◦,20◦三个迎角下,仿雨燕翼的升阻比相对于普通三角翼分别减小72%,43%,29%.从前缘斜切效果来看,对于普通三角翼,前缘斜切使升力减小,阻力也减小,小迎角(小于8◦)时升力阻力减小幅度类似,因此升阻比变化不大,迎角继续增大,升力减小幅度增大,阻力减小幅度降低,因此升阻比小于无斜切情况.而由于斜切角为30◦,60◦时的升力阻力变化幅度类似,因此这两个模型的升阻比较为接近.对于仿雨燕三角翼,由于斜切角为60◦时更明显的增升减阻作用,该模型的升阻比相比无斜切模型有显著的增大,迎角越小,增大越明显.迎角为2◦时,增大幅度为414%,而迎角为10◦时,增大幅度为41%,而迎角为18◦时,增大幅度仅为3%.相比之下,斜切角为30◦时,由于迎角大于8◦时,阻力系数会明显大于无斜切情况,所以此时升阻比变化比斜切角为60◦时更复杂.具体来说,迎角小于14◦时,斜切模型升阻比比无斜切模型更大,迎角大于14◦时,升阻比较小.迎角为2◦时,升阻比增大幅度为167%,而迎角为10◦时,增大幅度仅为19%,而迎角为18◦时,升阻比降低了6%.

2.2 涡流演化特性

近期的众多研究结果表明,飞行动物翅膀产生的前缘涡可以在升力产生和机动飞行中发挥重要作用[33-37].从上节的气动力系数变化情况可知,迎角和斜切角共同决定了三角翼上翼面的涡流发展特性以及总体气动特性.由于三角翼的总体气动特性与上翼面的涡流发展和演化特性紧密相关,本节以数值模拟结果为基础,探讨了不同情况下前缘涡的结构特征以及翼面的压力系数和摩擦系数变化情况.

图5 是六个不同三角翼模型在三个选定迎角(0◦,10◦,20◦)下涡核附近的流线对比图,而图6 是相应的物面在不同流向位置(x/l=40%,80%)的压力系数CP的对比图,图7 是物面在不同展向位置(2y/b=0,50%)的压力系数CP的对比图,图8 是物面在不同展向位置(2y/b=0,50%)的摩擦系数Cf的对比图.三角翼涡流起源于上下翼面之间强烈的压差引起的对流[38-40],压差越大,涡流强度也越大.从图5 中每个模型在三个不同迎角下的涡流结构来看,迎角越大,上下表面压差越大,涡流强度越大(最小压力值越小).对于普通三角翼,迎角为0◦时,主涡位置靠近前缘,而迎角增大到10◦,主涡位置向对称面移动,迎角继续增大,主涡位置没有明显变化,但是涡流结构在接近后缘位置发生明显膨胀.此外,值得注意的是,对于前缘斜切60◦,迎角为0◦的情况,由于前缘斜面的对流动的加速作用,来流向下翼面聚集,所以上翼面没有涡流产生.对于仿雨燕三角翼,在迎角和前缘斜切角都较小的情况下,后缘的滞止区在来流的诱导下会形成沿着后缘的涡流,该涡流会在翼尖附近与上翼面的主涡融合.总的来看,相对于普通三角翼来说,仿雨燕翼后缘的收缩对上翼面主涡的位置和强度没有显著影响,但是会使涡核的膨胀/破裂位置固定在后缘附近,从而使上翼面一直保持为低压区.

从前缘斜切角来看,对于普通三角翼,前缘斜切角越大,上下翼面压差越大,涡流强度也越大(最大压力值越大),涡核膨胀位置更靠前.但是,对于仿雨燕三角翼,由于后缘收缩后形成的滞止区涡流,前缘涡的形成和发展受到显著影响.迎角为0◦时,对于没有斜切,以及斜切角为30◦的两个模型,上翼面主涡和后缘涡在翼尖融合,对于斜切角为60◦的情况,来流向下翼面聚集,所以上翼面没有涡流产生,但是后缘涡仍然存在.迎角为10◦时,无斜切情况下还存在后缘涡,而有斜切的两个模型后缘已经没有后缘涡产生,从主涡来看,斜切角为30◦时涡流强度较大.迎角为20◦时,三种斜切角模型均没有后缘涡产生,斜切角为30◦时涡流强度较大.

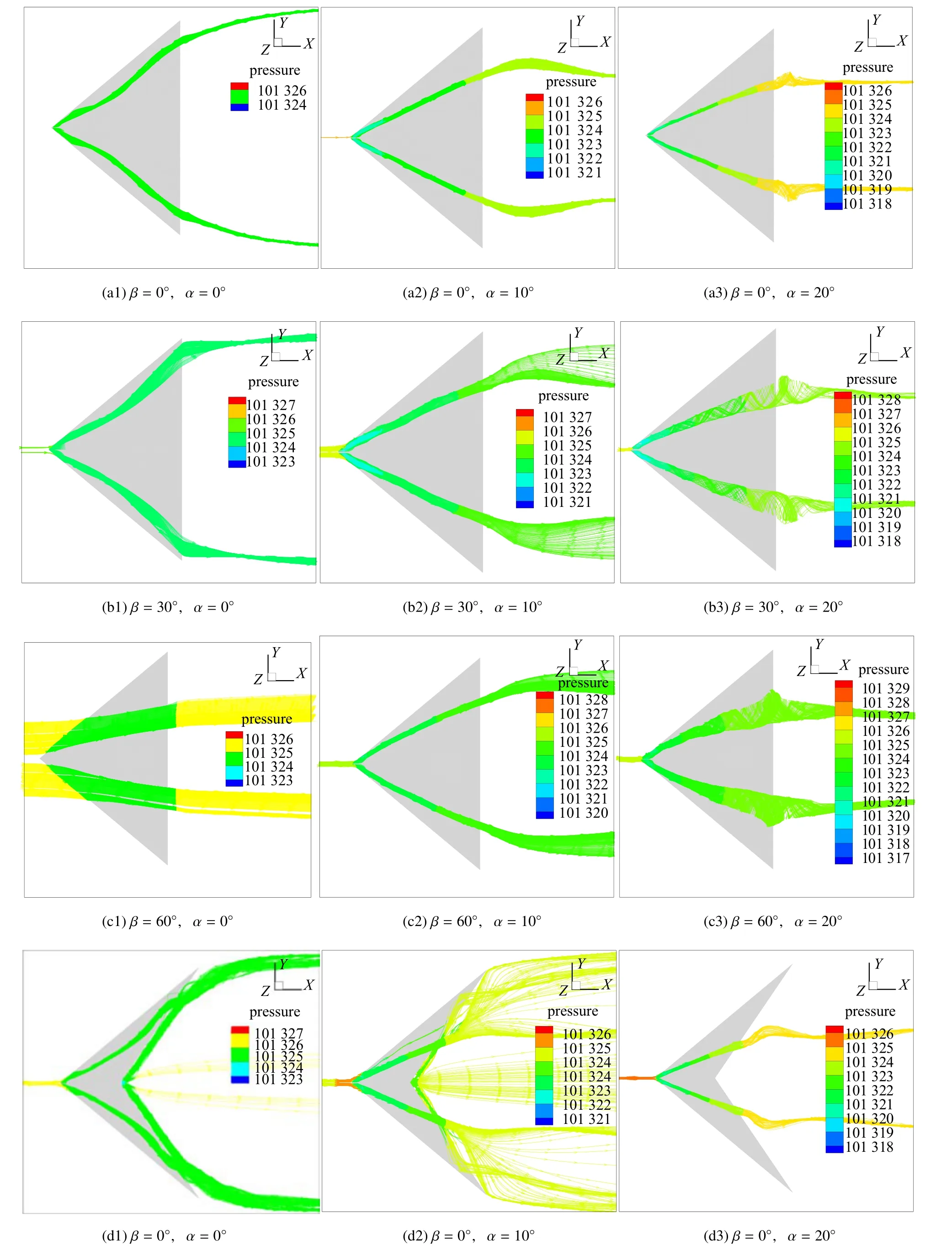
图5 不同模型不同迎角时背风区涡流结构对比Fig.5 Comparison of leeward vortical structures at different angles of attack for different models

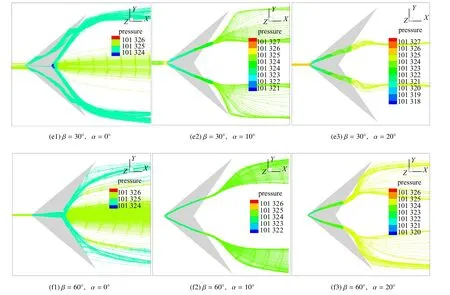
图5 不同模型不同迎角时背风区涡流结构对比(续)Fig.5 Comparison of leeward vortical structures at different angles of attack for different models(continued)

从图6 和图7 来看,对于普通三角翼,前缘斜切角越大,下翼面涡核位置对应的低压值越小,因为升力来源于上下表面的压力差,所以前缘斜切角越大,下表面压力越小(0◦迎角时甚至比上表面相应位置压力还小),升力损失越严重.对于仿生三角翼,虽然斜切角对上翼面的压力改变不大,但是,由于后缘的突然收缩,前缘斜切面的高压区起到主要作用,因此,斜切角越大,升力越大.这也与图4(a)的结论一致.而由于上下表面的压差增大,相应的压差阻力也比较大.

图8 是不同模型物面不同展向位置处摩擦系数的对比图,摩擦系数定义为,由于剪应力与速度梯度成正比,所以在涡核附近位置会出现摩擦系数极大值点,图中的拐点代表物面的涡流分离或附着线.在对称面2y/b=0,迎角和斜切角变化时涡流的位置和强度有明显变化,这与摩擦系数的位置和强度变化刚好吻合.而在2y/b=50%位置,摩擦系数的位置随涡流的变化而变化,摩擦系数的数值没有明显改变.而由于阻力来源于物面压力和摩擦力的积分,由此可见,涡流强度和位置的改变引起的摩擦阻力变化很小,图4(b)中阻力的变化与涡流引起的压力变化关系更密切.

3 结论

本文采用数值模拟方法,对仿雨燕三角翼布局在低雷诺数(Re=1.58×104)流动条件下的气动特性进行了深入探索,定量研究了前缘和后缘几何特征对涡流结构和气动特性的影响规律,结果表明:

(1)总的来看,迎角和前缘斜切角决定三角翼上翼面的涡流强度,迎角决定流场中压力的最小值,而前缘斜切角决定流场中压力的最大值.

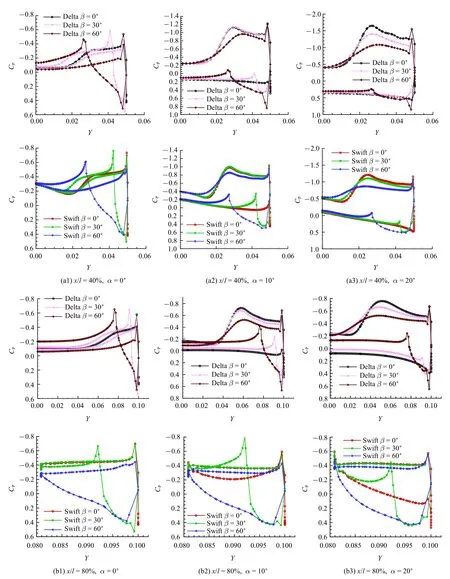
图6 不同模型不同迎角时弦向物面压力系数对比Fig.6 Comparison of chordwise pressure coefficient at different angles of attack for different models

图7 不同模型不同迎角时展向物面压力系数对比Fig.7 Comparison of spanwise pressure coefficient at different angles of attack for different models

图8 不同模型不同迎角时展向物面摩擦系数对比Fig.8 Comparison of spanwise skin friction coefficient at different angles of attack for different models

(2)前缘斜切对普通三角翼和仿生三角翼的升力影响效果刚好相反,前缘斜切角越大,仿生三角翼升力增大越明显,而普通三角翼升力降低越明显.

(3)仿生三角翼的收缩后缘使上翼面主涡的膨胀/破裂位置几乎固定在后缘处,因此上翼面一直存在稳定的涡流低压区,仿生三角翼的升力系数比普通三角翼大,小迎角下更明显.斜切角越大,增升效果越明显.

(4)由于后缘存在明显的后缘涡,并且后缘长度大于普通三角翼,仿生三角翼的阻力比普通三角翼大,并且主要是压差阻力而不是摩擦阻力.

数值模拟结果表明,相对于简单三角翼,后缘逐渐收缩的仿雨燕三角翼在低雷诺数、大前缘削尖角、小迎角的情况下具有明显的气动优势,是未来微型无人机的一个很好的气动布局型式.本文的研究局限于固定后掠的情况,没有考虑变后掠与翼变形引起的气动干扰效应,未来仍需继续深入研究.此外,未来需要深入研究左右非对称变形气动效应.

致谢本文全部数值模拟工作在新加坡南洋理工大学超性能计算中心Gekko 集群上完成,所需超算资源和计算费用由南洋理工大学机械与航空工程学院Chan Wai Lee 提供,在此特表感谢.