水下圆柱舱段模型耦合噪声源识别及空间声场定位研究

张 磊，李 彬，杨自春，陆英栋

（海军工程大学动力工程学院，武汉430033）

0 引 言

有限长圆柱壳体结构是潜艇等水下航行器舱段的典型结构形式。水下航行器的结构噪声来源于内部机械激励壳体振动，并带动周围流体介质振动产生声辐射，严重影响到航行器的整体声学性能[1]。在进行噪声控制时，主要从声源、传声途径和受主三个基本环节入手，而声源控制是噪声控制中最根本和有效的手段。因此，选用合理的声源定位和识别技术是至关重要的。

目前备受关注的声源识别方法主要有近场声全息技术和传递路径分析技术。近场声全息（Nearfield Acoustic Holography，NAH）技术[2]是利用声场中声源附近某一区域的声学量如复声压、复振速或声强，来预报其它区域的声特性，包括声源表面、近场及远场的各种声学量的空间分布。NAH 技术更加全面地利用了声场信息，抗干扰性好、可视化效果好，但目前难以识别内部声源和耦合性较强的声源[3-4]。传递路径分析（Transfer Path Analysis,TPA）技术[5-7]是处理声源（振源）—传递路径—目标测点的问题，TPA 技术可以确定各振源或声源传递的能量在总能量中的贡献，从传递路径的角度找出对辐射噪声起主导作用的环节，通过控制这些环节，如使振源（或声源）强度、路径声学灵敏度等参数在合理的范围内，以使水下声辐射控制在预定目标值内。但传统的TPA 方法实施过程繁琐、耗时，难以反映设备的动态特性[8-9]。

因潜艇等航行器内部机械设备众多、振动传递过程比较复杂，采用单一的噪声源识别方法会显得力不从心，而将不同的方法进行集成和融合是一条比较好的思路。为此，本文将综合运用融合新策略的NAH 和工况TPA 技术，优势互补，以圆柱舱段模型数值和试验分析为基础，实现圆柱壳体内部、外部耦合声源的识别和空间声场预报，进而为圆柱壳体的振动噪声控制提供强有力的支撑。

1 工况传递路径分析及声全息融合的噪声源识别技术

1.1 离散化柱面近场声全息技术

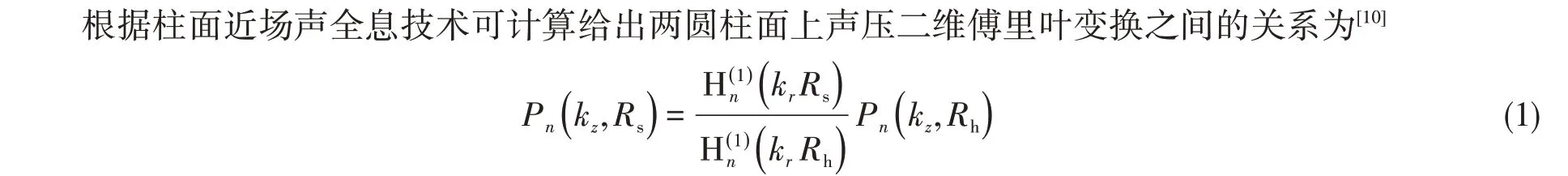
柱面NAH 的基本公式（1）是建立在柱面上连续采样点的基础上，然而实际测量只能在有限的离散点上进行，因此必须对公式进行离散化处理。因全息面为柱面，需分别对其轴向和周向进行离散化处理，这样使柱面沿某一条母线剪开后，展开面上的离散点呈网格状。全息测量面展开成平面的示意图见图1。测量面z轴方向高度为L，测量面半径为Rh，源面半径为Rs，离散时取z轴方向采样间隔为Δz，周向的采样间隔为Δθ。在z轴方向采样M列，周长方向采样N行。

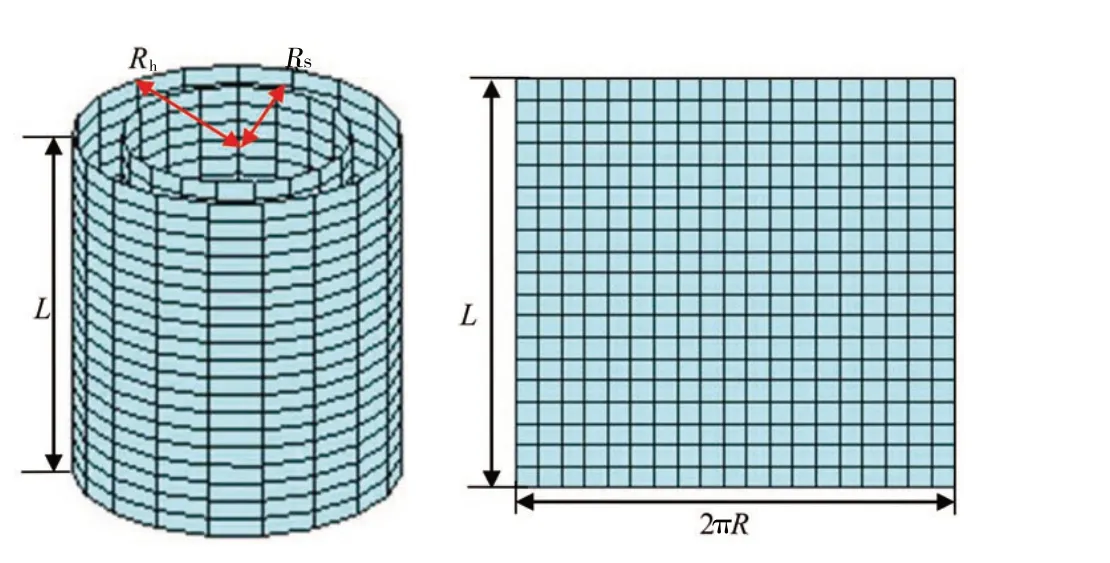
图1 柱面声全息离散示意图Fig.1 Discrete processing of a cylindrical surface

对于潜艇等圆柱壳体结构，其内部存在多个振动噪声源。这些噪声源共同作用，形成三维空间声场分布。由于声源位置相邻或重叠、传声器阵列大小、传声器数目及传声器之间的间距等因素的影响，NAH方法在某些情况下声源定位误差会比较大，难以有效地识别并分离出单个声源对空间声场的贡献。因全息面上测量得到的声压p(Rh,θ,z)是由多个振源共同决定的，通过式（1）的变换公式，不能重建出单个振源的结果。若要准确地重建出单个振源作用的结果，应首先对测量面上的声压响应进行噪声源识别，识别出各振源对测量面上声压的贡献。

1.2 基于系统辨识的OTPA方法

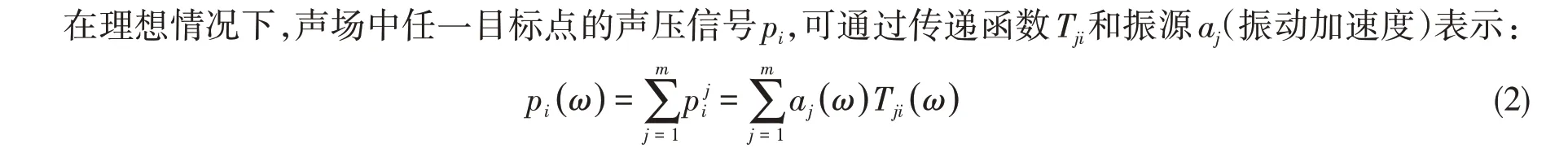
假设结构系统的传递特性函数是线性时不变的，对于r个不同的测量工况满足

式中，Hij为联结振源和观测信号之间传递函数，i=1,…,n1，j=1,…,m。将结构视为线性时不变系统，可定义结构中联结振源和观测信号之间的传递函数是线性且在试验过程中无明显变化，那么公式（4）在任意工况下均成立。若结构内部机械设备均可单独开启，如振源k单独开启，则sj=0(j≠k)，对于任一振源单独开启的工况r，式（4）均成立，满足式（5）：

1.3 SIOTPA-NAH 方法建立

2 水下圆柱壳体振源识别仿真分析

本章首先通过数值仿真模拟来验证上述SIOTPA-NAH 法在噪声源识别中的有效性。仿真模型为浸入水中的一封闭钢质圆柱壳体结构（如图2），轴向长度L1=2 m，半径Rs=0.3 m，密度ρ=7 800 kg/m3。声波在水中传播速度c=1 500 m/s。沿圆柱壳体Z轴（即母线方向），在圆柱壳体内部分别设置三个激励力模拟设备激励：F1激励点坐标为（0 m，-0.3 m，0.84 m），F2激励点坐标为（0 m，-0.3 m，0.12 m），F3激励点坐标为（0 m，-0.3 m，-0.6 m），激励力的方向均沿着Y轴负方向，激励力频率范围为20-2 000 Hz。以Rh=0.35 m 处的圆柱面为全息测量面，取测量面轴向长度为L=3 m，在全息测量面上取轴向采样间隔为Δz=L/M= 3/51，轴向采样间隔为Δθ= 2π/N= 2π/37。

图2 圆柱壳体结构模型Fig.2 Finite element model of a cylindrical shell and load location

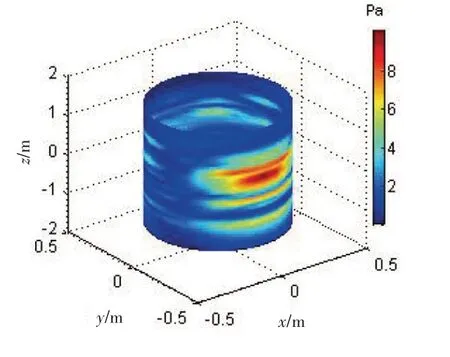
图3 圆柱壳体全息测量面声压云图Fig.3 Sound pressure distribution of the holographic surface

当三个激励力在某一激励能量同时作用时（F1=2 N，F2=2 N，F3=0.6 N)，计算得到全息面上的声压响应。具体计算过程为：利用Ansys 软件建立圆柱壳体的有限元模型，并计算出三个振源作用下的振动响应；将Ansys 计算结果导入Virtual lab 软件，利用Acoustic 模块中的边界元模块实现水下声场的计算，计算工况分为三个激励力单独和全部作用的情况；提取相应的振源测点、参考测点的振动响应值和全息面声压值，作为分析的基础数据，此处取典型频率1 707 Hz为例进行分析，由全息面上的数据可重建声源圆柱面或其他半径圆柱面上的声压信息，全息面测量的声压幅值分布如图3 所示，纵坐标为轴向z，横坐标为展开角度。由全息面测量声压，依据公式（10）可反演出圆柱壳体表面声压分布如图5 所示，重建结果与直接测量结果（图4）比较可以知，重构结果与直接测量结果声场空间部分吻合较好，准确地定位出声场中声压响应最大的位置，只有幅度上略有差异。说明柱面NAH 声场重建公式能够较准确地重构出空间声场。

图4 圆柱壳体展开表面实测声压云图 Fig.4 The measured sound pressure of the cylindrical shell surface

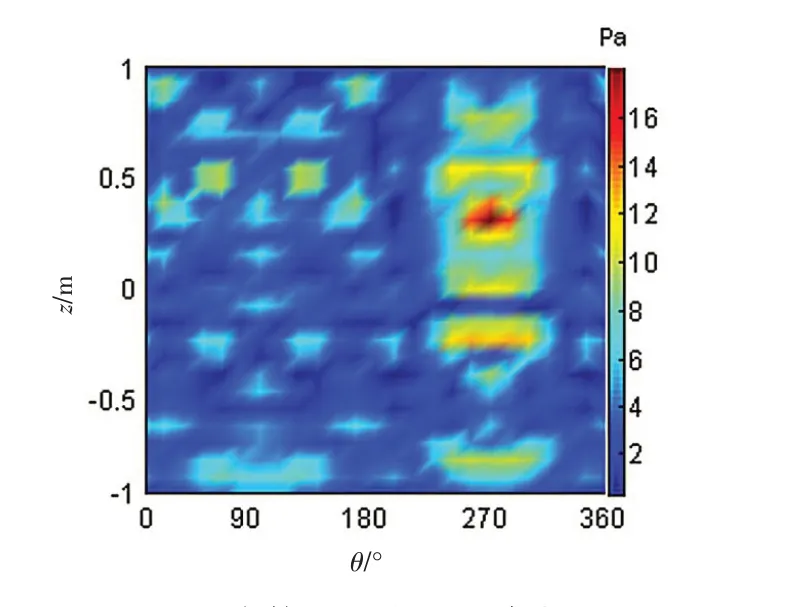
图5 圆柱壳体展开表面重建声压云图Fig.5 The reconstructed sound pressure of the cylindrical shell surface

图5为三个激励源同时激励时，圆柱表面的重建声压分布。因各声源之间相互影响，从图中我们难以判断出单个声源作用时的声压空间分布以及具体的贡献大小。这势必给声源的空间准确定位、减振降噪措施的有效实施等带来极大的难度。

为此，利用SIOTPA 方法计算各声源对全息测量面声压测点的贡献。SIOTPA 法实施时，取振源为振动加速度响应，需要特别注意振源测点和参考测点的选取。振源测点选择应遵循：能反映激励设备运行特性的测点；测点具有较高的信噪比。参考测点的选取应遵循：避免选取振动效应雷同的测点；各测点振动值大小应尽可能处于同一个数量级。算法中取振源数m=3，参考点数n=2m=6，工况数为r=4。然后，由式（9）～（10）便可实现SIOTPA-NAH方法。

利用SIOTPA-NAH 法进行声场重构，可较好地重构出单个振动源产生的辐射声场空间分布情况，如图6～7 所示。图中SIOTPA-NAH 法计算结果（如图6 所示）与直接测量声压空间分布（如图7 所示）比较一致，主要的声源位置以及响应的幅度大小均吻合较好，计算精度满足水下噪声分析的基本要求。声源间存在一定的相互影响，识别结果中的声场分布比理论计算结果偏大一些，但声源位置与实际位置非常接近。从图8可以看出，单个振源的声场重建结果与实际声压分析的误差基本保持在3 dB 之内。造成误差的原因可能为声全息公式计算产生的误差，以及仅考虑了y向的激励和响应却忽略了x向和z向贡献导致的误差。

图6 1#振源作用下圆柱面重建声压分布云图 Fig.6 The reconstructed sound pressure of the cylindrical shell surface with#1 excitation force

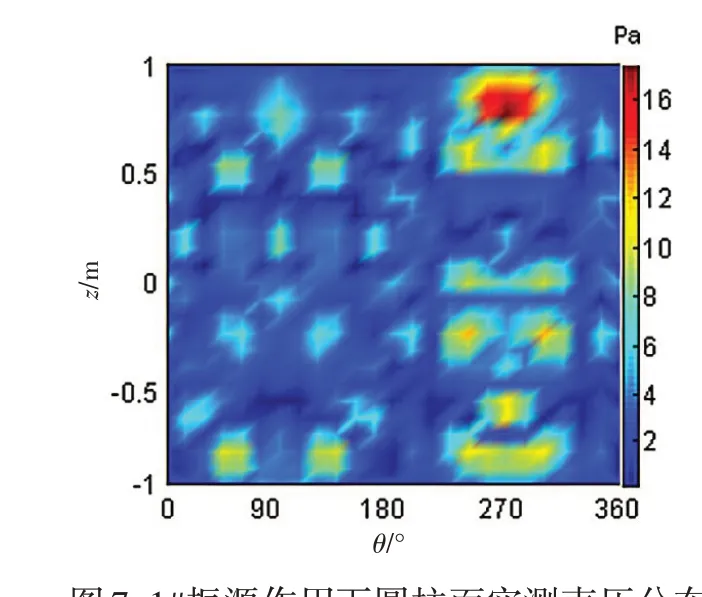
图7 1#振源作用下圆柱面实测声压分布云图Fig.7 The simulated sound pressrue of the cylindrical shell surface with#1 excitation force

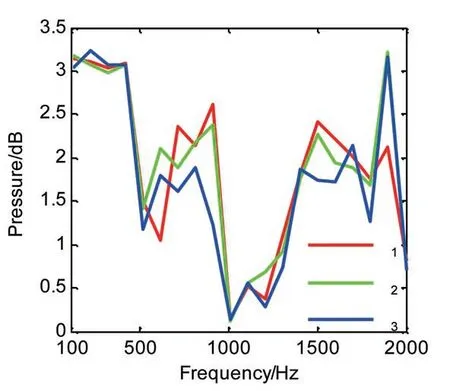
图8 单个振源的声场重建声压与实测声压误差图 Fig.8 Reconstruction error curve of each vibration source

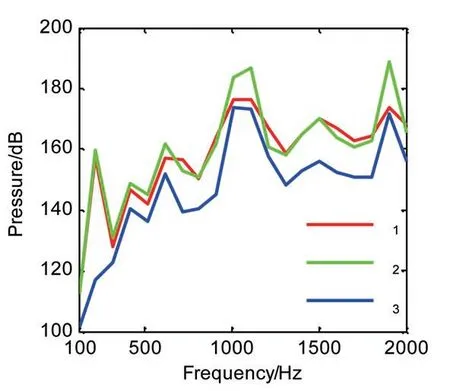
图9 各振源对圆柱表面声场的总贡献量Fig.9 Total contribution curve of each vibration source

SIOTPA-NAH 方法可以识别出各个振源对声场中任意测点的贡献量，图9 所示为不同频率下各振源对圆柱表面声场的总贡献量，从图中可以看出不同频率处各振源的噪声贡献量可能是不一样的，而频率相同各振源对目标点的贡献量也会是异同的，这些都可通过SIOTPA-NAH 方法进行定性和定量的分析。从图中可以看出：1 707 Hz时振源的贡献量排序为1#＞2#＞3#；峰值频率1 010 Hz处振源对重建空间声场的贡献量排序为2#＞1#＞3#；整个频率范围内，三个振源对重建声场空间的总声压级分别为181.8 dB（1#）、191.8 dB（2#）、177.7 dB（3#），即贡献量排序为2#＞1#＞3#。因振源中3#振源激励力最小，所以其对声场空间的贡献就较小。振源1和振源2的激励力大小相同，由图9可见，在整个频率范围内2#振源对声场的贡献在部分频段与1#振源相当，但2#振源在某些频段出现较大峰值，致使2#振源对声场空间贡献更大。可见，振源对声场的响应大小不仅取决于振源的大小，而且还取决于振动-声的传递路径，本文提出的SIOTPA-NAH 方法也可进行振源及其传递路径特性分析，同样可以得到各振源对三维空间声场任意一个目标的贡献量。可见SIOTPA-NAH 方法能够克服噪声源识别和声场预报的盲目性和主观随意性，得出有益、可靠的结论。

3 水下舱段模型振源识别试验分析

为进一步验证文中提出的SIOTPA-NAH 方法在噪声源识别和声场预报中的有效性，开展了某单层壳体舱段模型水下声振特性测试。实验在某消声水池开展，模型长度为2.26 m，半径为0.7 m，布放深度约为水下5 m，典型试验模型和激振设备如图10所示。全息面声压采用扫描设备测量，将水下扫描机构安装到舱段模型上，扫描环上装水听器探头，水听器安装时须注意水听器探头到舱段模型表面的距离应一致。测量参数包括：舱段中心与水听器距离635 mm，扫描面轴向测量范围1 680 mm，周向测量范围312°以及扫描间隔60 mm×12°。将参考水听器或加速度计固定到舱段模型上或指定位置，测量水域近似满足自由声场条件。分别在舱段模型内不同的位置布放三台激振器，以模拟舱段内部多个设备同时开启的状态，激励器在不同的频率和能量下激励。取采样频率为2 048 Hz，采样点数为20 480。

利用文中建立的SIOTPA-NAH 方法进行舱段模型圆柱表面噪声源识别，以两个激励设备（1#、3#激振器发出连续正弦信号，功放幅值分别为72 Vpp和92 Vpp）同时开启的工况为例进行分析，分析频率为1 kHz。图11为两个激励设备同时开启时，全息测量面的声压分布情况，由柱面声全息算法重建的圆柱表面的声压分布如图12（反演面与声源距离为5 mm）所示，图中清晰地显示了两个激励源作用时，圆柱表面的声压分布情况，但由于声源之间相互影响，从图中难以分辨出单个振源在圆柱表面的声压贡献。

图10 舱段模型及激振器位置Fig.10 The experimental model and exciters’positions

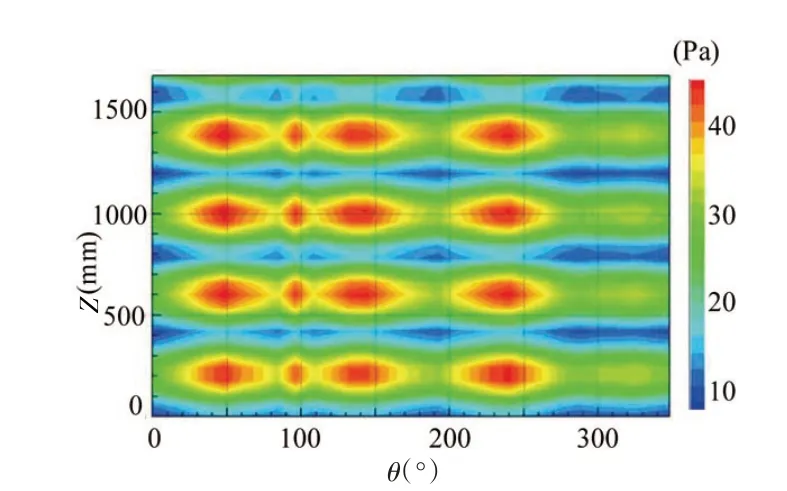
图11 圆柱舱段全息测量展开平面声压云图 Fig.11 Sound pressure distribution of the holographic surface

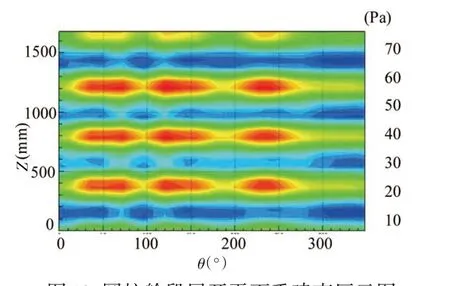
图12 圆柱舱段展开平面重建声压云图Fig.12 The reconstructed sound pressure of the cylindrical shell surface

为此采用SIOTPA-NAH 方法计算出单个激励源作用时圆柱表面的声压响应分布，如图13～14 所示，该算法计算的声压分布情况与实际测量的声压分布比较一致，能够准确地定位出主要振动源的位置。因此，利用传统的声全息方法很难将较小的声源对整个声场的影响比较准确地分析出来，而且识别出的声源位置也常与真实振源位置存在偏差。但利用SIOTPA-NAH 方法可以分离出单个振源在声场中的贡献，进而重构出较为准确的空间声场分布。同样，可以给出振源对重建空间声场的贡献量分析，两个振源在圆柱壳体表面的声压幅值总贡献量的排序为3#激励器＞1#激励器，与实际完全一致。

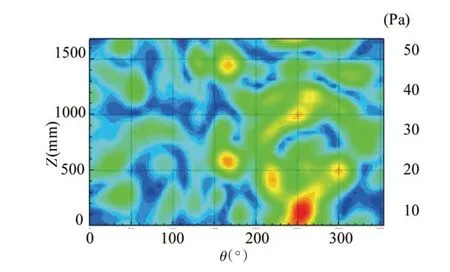
图13 1#振源作用下重建声压分布云图 Fig.13 The reconstructed sound pressure of the cylindrical shell surface with#1 excitation force

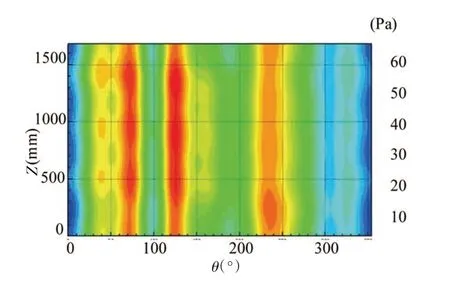
图14 3#振源作用下重建声压分布云图Fig.14 The reconstructed sound pressure of the cylindrical shell surface with#3 excitation force

4 结 论

（1）离散化的柱面NAH 声场计算公式能够较准确地重构出空间声场，并定位出圆柱壳体表面声压或振速分布，但难以判断出单个声源作用时声压空间分布以及具体的贡献量大小。

（2）OTPA 方法面临的振源间交叉耦合问题将导致在振源识别时误差增大，乃至失效，SIOTPA 方法将多振源视为卷积混叠，基于系统辨识思想分析得到了去除交叉耦合的振源，提升了OTPA 方法在振动源及其传递路径识别时的精度和稳定性。

（3）建立了一种功能强大的耦合声源识别和声场预报的SIOTPA-NAH 方法，准确地识别出了耦合振源中多个振源量值、振源对声场中任意测点的贡献量、振源对声场测点的传递路径，并实现了单个或多个振源可视化声场预报，以及声源表面的准确的可视化定位。研究成果对采取针对性的减振降噪措施降低潜艇等圆柱舱段的噪声水平、控制引起暴露的声学特征具有重要意义。