基于柔性杆理论的脐带缆涡激振动数值模拟系统

顾洪禄，郭海燕，李效民，刘 震，李 朋，王宣淇

（1.中国海洋大学工程学院，山东青岛266100；2.山东科技大学土木工程与建筑学院，山东青岛266590）

0 引 言

脐带缆是浮式生产系统中重要装备之一，主要用于电力的传输和信号的控制[1]。脐带缆在运行期间始终受到海流的作用，在一定流速下，脐带缆两侧形成交替的漩涡，漩涡脱落会引起脐带缆结构产生周期性的振动，称为涡激振动。当漩涡脱落频率接近脐带缆固有频率时，脐带缆振动会加剧[2]。这不仅会导致脐带缆的疲劳破坏，还会引起脐带缆内部光纤发生破坏，导致通信中断，严重威胁整个油气的安全生产。因此，研究脐带缆的涡激振动现象在工程实践中有着很重要的意义。

涡激振动的预报模型主要分为CFD 模型和经验模型两大类。CFD 模型由于计算量较大，还难以直接应用到实际的海洋工程问题中，因此，脐带缆涡激振动的数值模拟目前仍主要依赖于经验模型[3]。在现有的经验模型中最具有代表性的分析软件当属Shear7[4]。Shear7 基于结构小变形假设和大量试验获得的涡激力模型预测结构的涡激振动响应，用Shear7 计算钢悬链线脐带缆的涡激振动响应没有考虑悬链线结构的大变形特性，Shear7所预报的横向涡激振动响应比试验数值偏大5%左右[5-6]。目前基于柔性杆理论以及尾流振子模型进行软件的开发尚未见有报道。

本文基于柔性杆理论和Facchinetti[7]推荐的尾流振子模型开发了脐带缆涡激振动数值模拟系统UCVIV-1.0，充分考虑了柔性管缆大变形、大转角的结构几何非线性以及结构与外部流体的线性耦合项，可以直接求解脐带缆在任意剖面形式下海流作用下的涡激振动响应，相比于Shear7等软件更接近于工程实际。UCVIV-1.0 界面清晰简洁，操作方便。随着研究的不断深入，UCVIV-1.0 将会升级为包括缓波形、陡波形在内的功能齐全的海洋管缆分析软件，最终应用于我国海洋管缆实际工程设计中。

1 计算原理

1.1 柔性杆模型

在柔性杆理论中，杆的位形由杆轴线位置表示，如图1 所示，在三维笛卡尔坐标系中空间曲线r(s,t)表示柔性杆变形后轴线位置状态，它是杆弧长与时间的函数。该模型的最大优点是其控制方程直接在全局坐标系下得到，而且还包括了全部几何非线性，省却了不同坐标系之间繁琐的坐标转换，可以非常有效地解决脐带缆的大变形问题。

假设变形前后杆的弧长不发生改变，脐带缆上任意一点的内力状态可以完全由作用在轴线上的合力和力偶表示，并且忽略转动惯量和剪切变形的影响。由动量守恒和动量矩守恒可得[8-9]

式中，ρ是单位长度质量；q是单位长度分布外力；m是单位长度分布外力矩；F是轴线上的合力；r'代表对弧长s求一阶导数；r̈代表对时间t求二阶导数。M是截面弯矩和扭矩H之和，则内力矩M可表示为

式中，EI为抗弯刚度，H为截面扭矩。通常脐带缆等细长柔性杆结构可以忽略均布扭矩和分布外力矩的作用，令H=0，m=0，将式（3）代入式（2）可得

图1 柔性杆模型示意图Fig.1 Diagram of slender rods

式中，λ(s,t)是标量函数。将式（4）代入式（1）得柔性杆的运动方程为

1.2 荷载分析

脐带缆处于复杂的海洋环境中，受到自身重力、周围流体水静力和水动力的作用，柔性杆的外荷载可以表示为

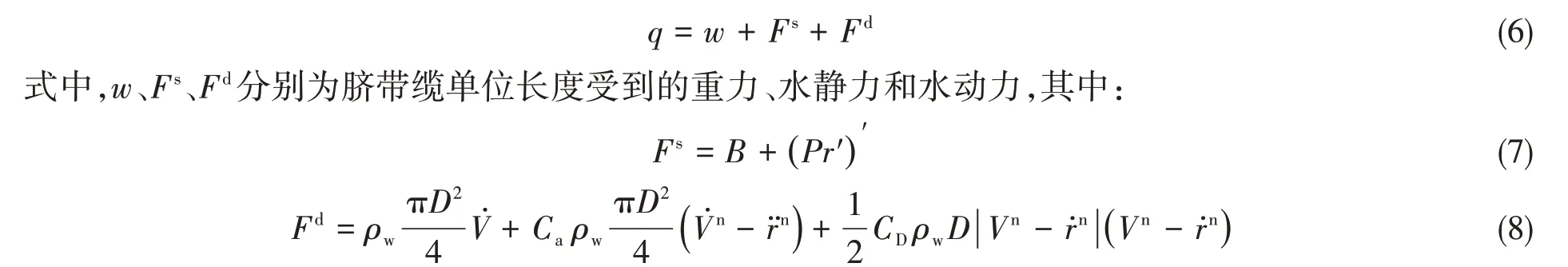
式中，B是单位长度浮力，P是脐带缆内外压力差，ρw是海水密度，Ca是附加质量系数，CD是拖曳力系数，D是缆体外径，V是水流速度。

1.3 有限元离散

将柔性杆运动方程和变形条件分别写成张量形式：

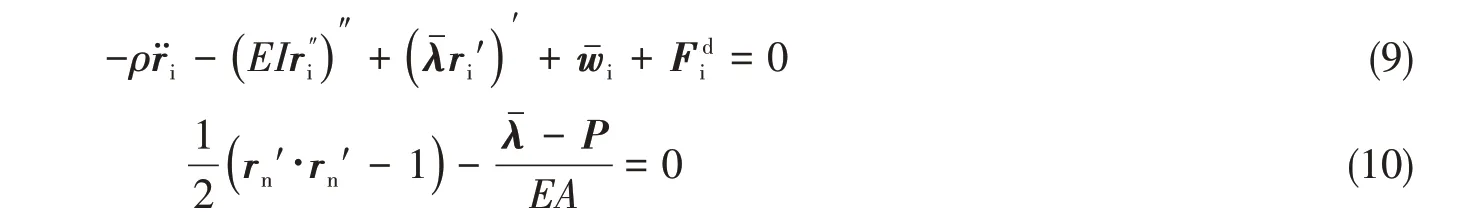
式中，有效重力wˉ=w+B，有效张力λˉ=λ+P。张量形式的方程通过采用三次Hermit 插值函数进行离散后，运用Galerkin方法得到矩阵形式的微分方程如下：

1.4 静力分析

采用Newton-Raphson 方法迭代求解非线性方程式（11）和（12），同时忽略方程式（11）中的惯性力项，最后矩阵形式如下[10]：

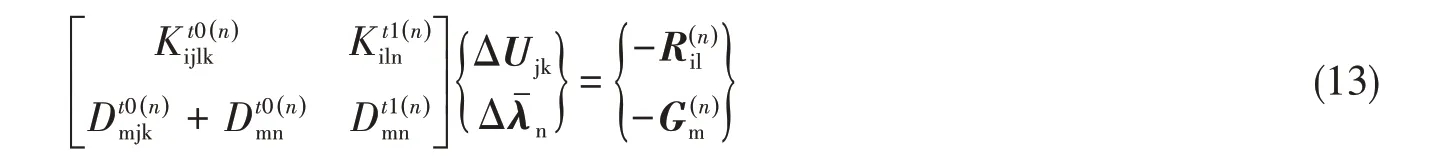
由于方程式（13）中的下标表示方法不方便编程求解，对未知量Ujk和λˉn重新编码为y。方程式（13）可改写为

1.5 尾流振子模型

将脐带缆单元涡激振动耦合振动方程组（11）加入升力项之后与式（12）、式（16）分别集合便可获得整体耦合方程组的矩阵表达形式：

采用Newmark-β迭代算法对脐带缆整体耦合控制方程（17）-（19）进行逐步积分，求解尾流振子模型涡激力作用下脐带缆的涡激振动响应。

2 用户界面设计

脐带缆涡激振动数值模拟系统（Numerical Simulation System of Vortex-Induced Vibration of Umbilical Cable，简称UCVIV-1.0）是以MATLAB 7.6.0 为平台，使用图形用户界面GUIDE 开发的人机交互界面，以图形、动画、数值等方式展示结果，可用于海洋脐带缆在海流、波浪、顶部浮体等荷载联合作用下的静力分析和涡激振动分析。

本系统主要包括三大模块：系统的前处理模块—参数输入模块（包括脐带缆参数、流体参数、波浪及浮体参数）；系统的核心模块—分析计算模块（包括静力计算、VIV 计算）；系统的后处理模块—结果输出模块（包括图形结果和数值结果）。

2.1 参数输入模块

本模块主要使用Edit Text、Push Button 和Pop-up Menu等组件将用户输入的数值转化为字符串储存起来，为分析计算模块提供准确无误的基本参数，界面如图2～4所示。

图2 脐带缆参数输入界面Fig.2 Umbilical cord parameter input interface

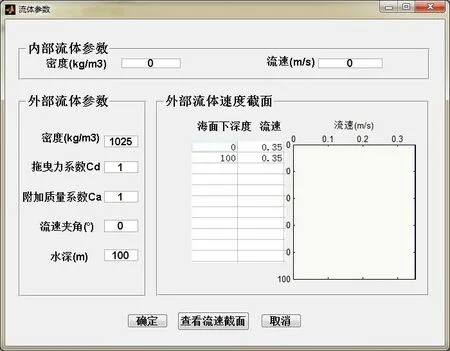
图3 流体参数输入界面Fig.3 Fluid parameter input interface

2.2 分析计算模块

分析计算模块是本系统的核心模块，考虑脐带缆重力和浮力、浮体偏移、波浪及海流荷载的作用，对简单悬链线型脐带缆进行静力分析和涡激振动分析。在进行涡激振动计算分析时，采用Matteo Luca Facchinetti[7]推荐的尾流振子模型，该模型容易扩展到二维和三维的涡激振动，且与实际情况更为符合。

2.3 结果输出模块

2.3.1 静力分析结果

显示脐带缆的静力位形、有效张力和弯矩计算的图形结果。

2.3.2 VIV分析图形结果

图形结果分为五部分：任意一点位移时程曲线、任意时刻位移曲线、最大位移包络图、任意一点张力时程曲线和最大张力包络图。图形结果界面将直接显示最大位移节点、最大张力节点、最大张力和最大位移等信息。点击界面的编辑图形按钮可以进入MATLAB图形编辑器，可以对系统获得的原始图形进行多种后处理，获得更为理想的图形结果。

图4 波浪及浮体参数输入界面Fig.4 Input interface for wave and floating body parameters

2.3.3 VIV分析数值结果

本模块使用VideoSoft FlexArray Control 控件以表格形式显示数值结果[11]，从表格中可以很清晰地看到每个节点的最大张力和最大位移的数值，极值对应节点加粗显示。数值结果只能查看不能编辑、导出。

3 实例分析

3.1 模型验证

选取参考文献[12]的脐带缆参数，脐带缆空气中单位质量为116 kg，抗弯刚度EI=2 870 N∙m2，轴向刚度EA=3.52×108N，海水密度为1 024 kg/m3，脐带缆外径为0.254 m，脐带缆总长190 m，顶部偏移为150 m，水深为100 m，海流为+X方向，速度为0.35 m/s，波高为6 m，周期为5 s。

为验证系统的准确性，将本文计算得到的简单悬链线型脐带缆的平衡位形、有效张力和弯矩分别与相同参数条件下商业软件OrcaFlex 的计算结果进行对比，如图5～7 所示。由图可知，本文的计算结果与OrcaFlex的计算结果吻合较好，一定程度上说明了计算系统的可行性。OrcaFlex计算的弯矩在躺地段比本文计算结果略高，这是本文与OrcaFlex选取的海床模型不同所导致。

图5 位形结果比较Fig.5 Comparison of configuration results

3.2 实例计算

选取3.1节脐带缆的基本参数，利用UCVIV-1.0进行实例计算，结果如图8～13所示。计算结果表明在t=59 s，距离底端点81.7 m 时，脐带缆涡激振动产生最大的水平位移，约为3.155 8 倍的脐带缆外径；脐带缆的最大张力发生在悬挂点处，约为138.531 1 kN。

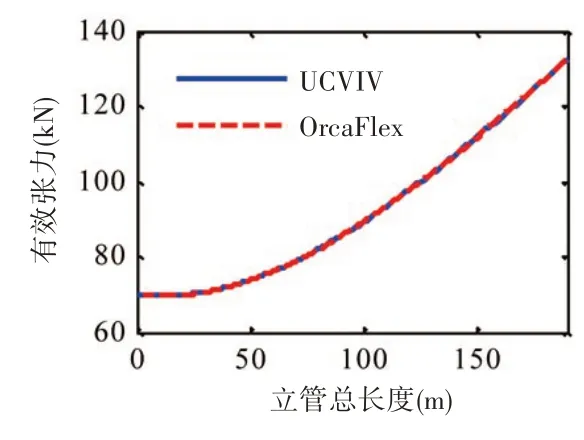
图6 有效张力结果比较Fig.6 Comparison of effective tension results

图7 弯矩结果比较Fig.7 Comparison of bending moment results

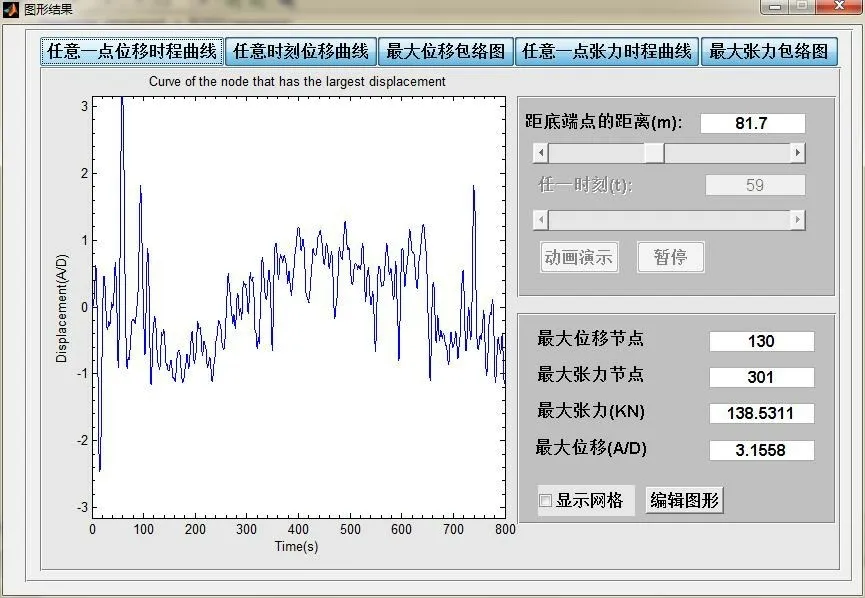
图8 任意一点位移时程曲线Fig.8 Displacement time history curve at any point

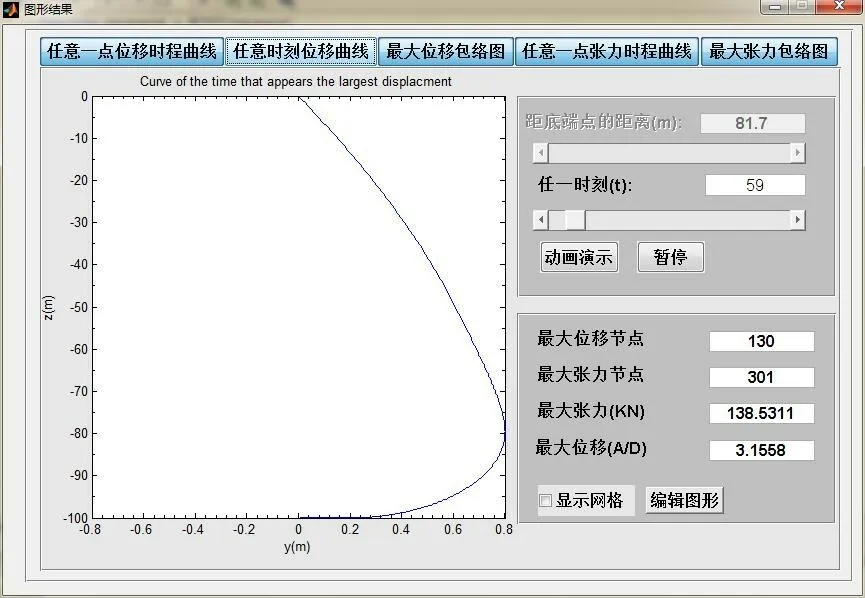
图9 任意时刻位移曲线Fig.9 Displacement curve at any moment

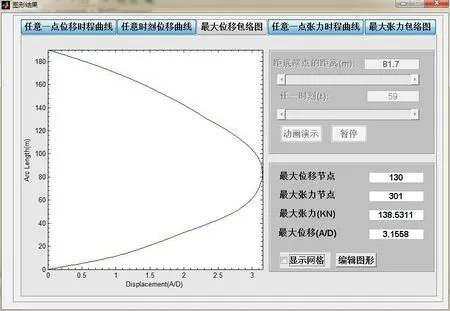
图10 最大位移包络图Fig.10 Maximum displacement envelope

图11 任意一点张力时程曲线Fig.11 Curve of tension at any point

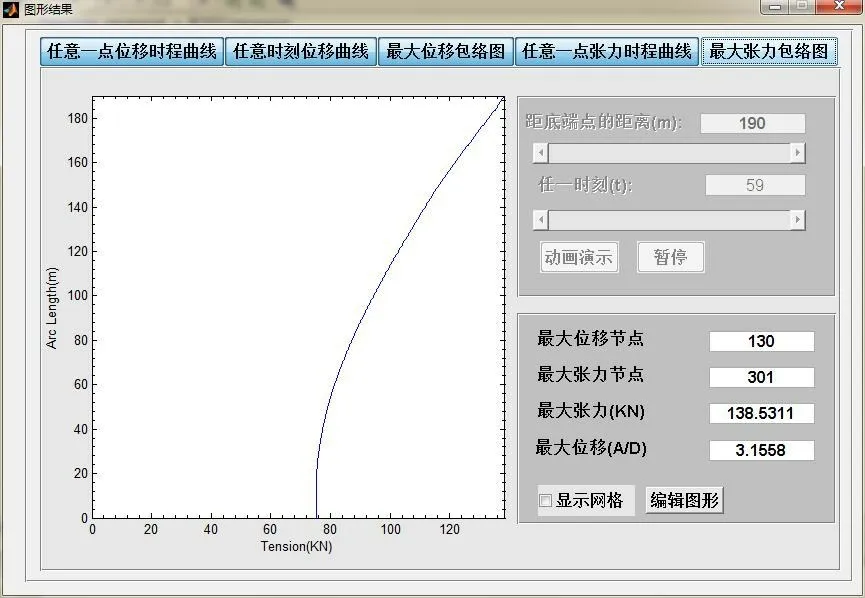
图12 最大张力包络图Fig.12 Maximum tension envelope

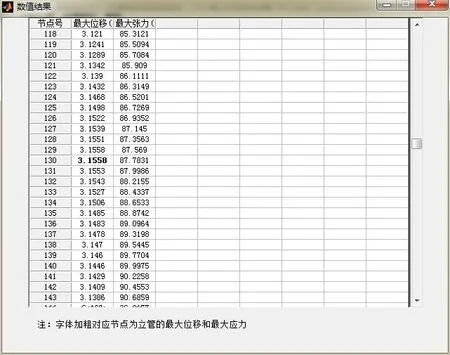
图13 数值结果Fig.13 Numerical result

3.2.1 外流流速大小的影响

不考虑波浪和顶部浮体运动的影响，并保持其他参数不变，选取0.20 m/s、0.30 m/s、0.35 m/s、0.40 m/s、0.45 m/s、0.50 m/s、0.55 m/s、0.60 m/s八级外部流速，分别计算脐带缆在800 s内涡激振动响应下的位移以及张力，并将结果进行对比，其中最大位移（A/D）通过立管外径进行了无量纲化，对比结果如图14～15和表1所示。

图14 最大位移及最大张力Fig.14 Maximum displacement and maximum tension

图15 最大位移位置及最大张力位置Fig.15 Position of maximum displacement and maximum tension

表1 不同外流流速下的计算结果Tab.1 Calculation results at different outflow velocities

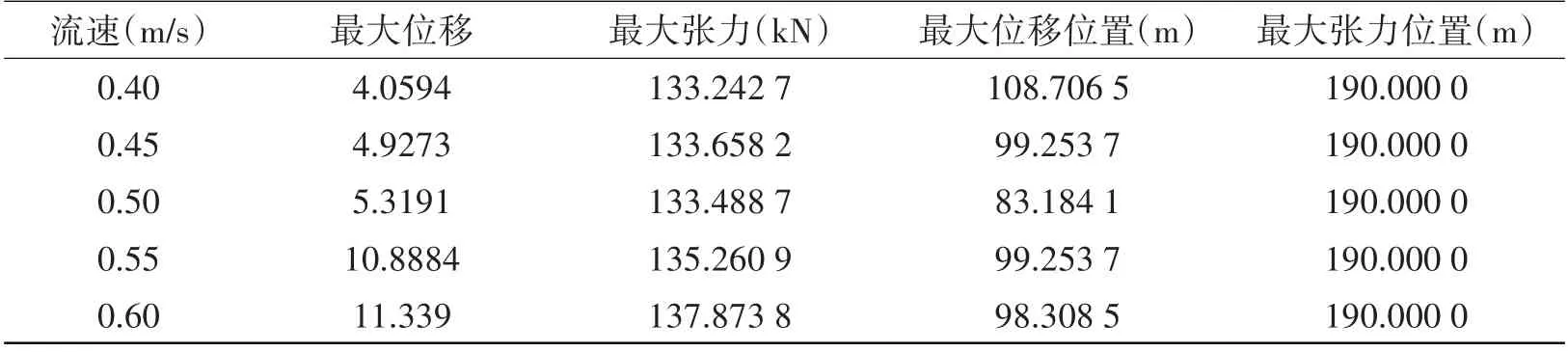
续表1

计算结果表明：随着外流速度的增加，最大位移一直增大；最大张力随外流速度的变化规律与最大位移基本一致，因为随着流速增加，脐带缆在海流作用下激起了更大幅值的模态，同时在海流的拖曳力作用下产生更大的轴向力，导致最大张力随流速增加而变大；最大位移节点位置在脐带缆1/2 总长位置附近上下浮动，这是由于脐带缆两端铰接限制了两端点附近的位移所导致；最大张力的位置一直不变，位于脐带缆的悬挂点处，主要原因是脐带缆的所有重量几乎全部作用于悬挂点，导致悬挂点承受的轴向张力值最大。由此可见，外部流速对于脐带缆涡激振动具有显著的影响，在实际工程设计中悬挂点、中心点处的设计计算十分关键。

3.2.2 弹性模量的影响

选取外流速度为0.35 m/s，保持其他参数不变，分别选取脐带缆弹性模量为E/3、2E/3、E、1.2E、1.5E计算脐带缆的涡激振动响应，并将结果进行对比，其中最大位移（A/D）利用立管外径进行了无量纲化，对比结果如图16～17、表2所示。

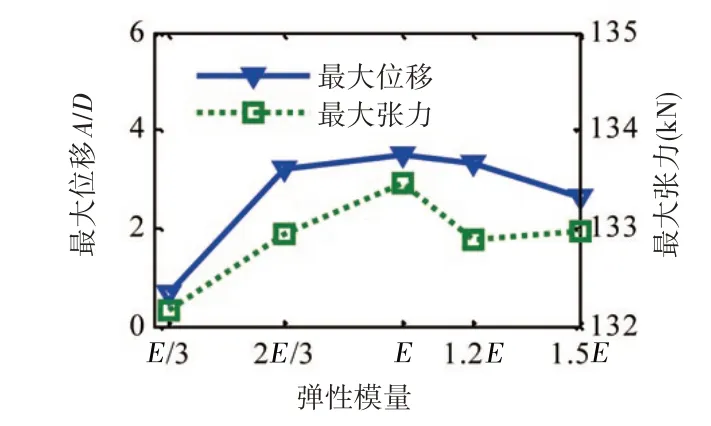
图16 最大位移及最大张力Fig.16 Maximum displacement and maximum tension

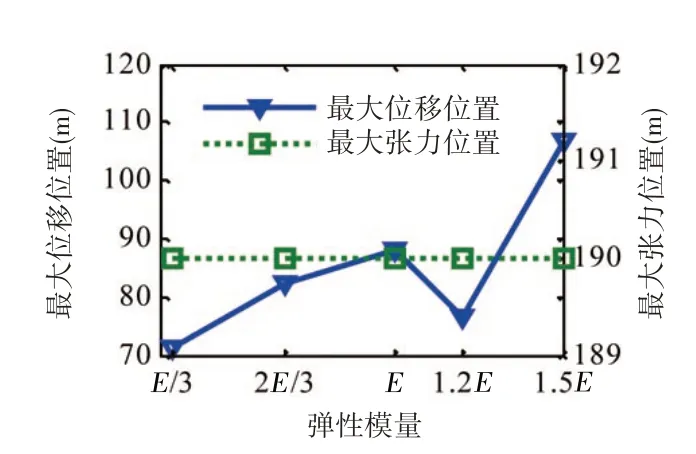
图17 最大位移位置及最大张力位置Fig.17 Position of maximum displacement and maximum tension

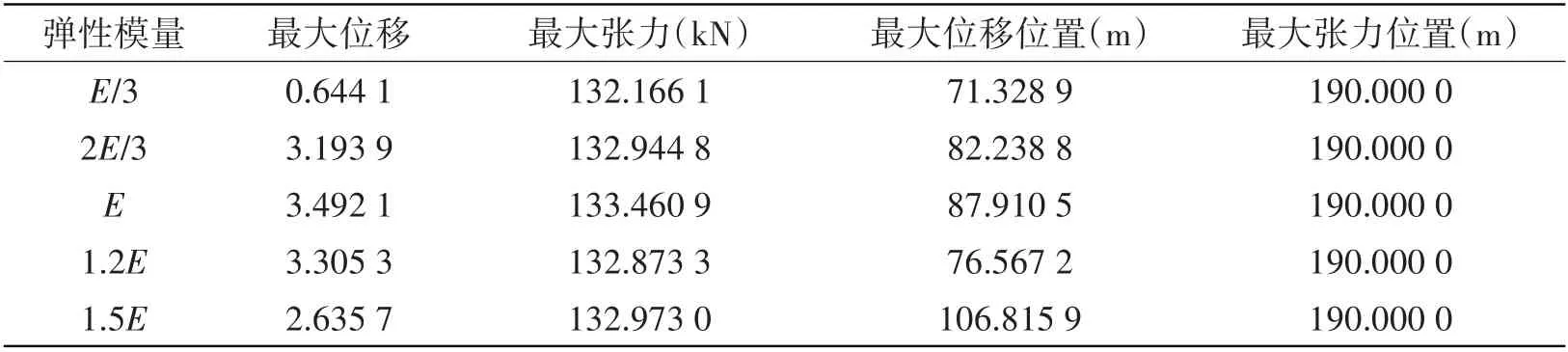
表2 不同弹性模量计算结果Tab.2 Calculation results with different elastic moduli

从计算结果可以看出，随着弹性模量的增加，最大位移在弹性模量为E时出现了极大值，这与文献[13]计算结果相符，因为弹性模量的改变直接影响了脐带缆的自振频率，脐带缆弹性模量为E时，脐带缆自振频率接近锁振区，振动幅值显著增大，随着弹性模量的变化，脐带缆自振频率逐渐脱离锁振区，振动幅值变小；最大张力稳定在133 kN 附近；由图17 可以看出，最大位移点随着弹性模量的增加出现了整体上移的趋势，但弹性模量在E和1.2E之间出现了逆反趋势，主要是由于弹性模量的改变导致了脐带缆响应模态的改变；最大张力位置与不同流速作用下的变化规律相同。因此，在实际工程中应控制脐带缆弹性模量的大小，建议选取低弹性模量高应力材料，即刚度较小且具有较高极限荷载的材料，这种材料可以保证在相同海流作用下脐带缆整体响应幅值较小并且具有较高的疲劳寿命。

4 结 语

本文基于柔性杆理论，采用尾流振子模型，以MATLAB为平台开发了脐带缆涡激振动数值模拟系统UCVIV-1.0。该系统分为参数输入模块、分析计算模块和结果输出模块，主要用于简单悬链线型脐带缆在海流、波浪和顶部浮体等荷载联合作用下的静力分析和涡激振动分析。该系统界面清晰友好，操作简单。本文选取参考文献[12]的脐带缆参数进行静力分析，并将计算结果与同样工况下商业分析软件OrcaFlex 的计算结果进行了对比，二者结果吻合良好，一定程度上证实了系统的可行性。最后用UCVIV-1.0对不同外流流速、弹性模量下的脐带缆进行了计算比对，发现外流流速以及弹性模量对脐带缆涡激振动的影响较大，高流速会导致脐带缆最大张力、最大位移显著增加；弹性模量主要通过改变脐带缆涡激振动的锁振区间影响脐带缆的最大位移；最大位移位置一直在脐带缆中心点上下浮动，脐带缆的全部质量基本作用于悬挂点处，导致最大张力位置一直处于悬挂点处。因此，实际设计中对于悬挂点和中心点处应进行详细设计计算。UCVIV-1.0 可为实际工程计算提供参考，并有望用于我国的脐带缆工程设计。