多层流化床床层及溢流管中气固流动特性的模拟

陈 城，杨 遥，黄正梁，孙婧元，王靖岱，阳永荣，李金安

1.浙江大学化学工程与生物工程学院，化学工程联合国家重点实验室，浙江 杭州 310027；2.郴州中化氟源新材料有限公司，湖南 郴州 424202

多层流化床出现已有60 多年[1]，但目前对多层流化床内气固流动的研究仍主要停留在宏观操作层面，包括床层及溢流管压降[2-4]、流化气速及固体流量[5]、颗粒平均停留时间[6]等。一方面，这是由于以往研究多是以应用为出发点，选用的实验装置多为体积相对庞大、更接近工业尺寸和结构的多层流化床装置，对床层内部尤其是溢流管附近的颗粒流动难以进行详尽的研究。另一方面，由于侵入式的检测设备会对多层流化床内部的流场产生影响，难以准确地获得流化床层内部尤其是溢流管附近区域的细节性数据。

随着计算机技术的快速发展，计算流体力学（CFD）模拟能够有效地获取流化床内的气固流动行为，且成本相对低廉，逐渐成为研究流化床内气固两相流场的一种重要方法。相比传统实验方法，采用计算流体力学模拟多层流化床，将有可能更加有效且系统地获取流化床层压降及溢流管内的气固流动特征，为研究溢流管内的颗粒流动以及溢流管与流化床床层间的相互作用提供助力。但是，在公开文献中尚未有学者将CFD 模拟的方法用于研究多层流化床反应器，这是因为对多层流化床反应器进行模拟将不可避免地涉及层间分布板的模拟，而分布板的直接建模涉及极为复杂的网格结构，导致计算复杂、模型收敛较难。本工作采用Fluent 商业软件，采用多孔介质模型模拟层间分布板，对多层流化床内典型颗粒层间传递单元进行建模及模拟，考察不同操作气速下，多层流化床内连续进出料情况下各床层和溢流管的气固流动行为，研究操作气速对相邻床层流化状态的影响及其对溢流管内颗粒流动的影响。

1 模拟对象

模拟的多层流化床物理模型尺寸参考Yang 等[7]所使用的双层流化床装置。为使模拟更具有代表性，对部分结构进行了修改，使其成为多层流化床的一个典型单元。由于流化床和溢流管均采用圆筒形结构，为保证模拟的准确性，采用三维模型进行模拟。如图1 所示，多层流化床的主体床层直径为240 mm，分为上下两个床层，上床层的高度为650 mm，中间分布板的厚度为30 mm，下床层的高度为620 mm。多层流化床内有三根溢流管，溢流管1 为出料溢流管，位于下床层底部一侧，中心位置距离多层流化床中心60 mm，溢流管高度为90 mm；溢流管2 为层间传递溢流管，位于两床层间，中心位置距离多层流化床中心60 mm，溢流管上出口距上床层分布板90 mm，下出口距下床层分布板75 mm；溢流管3 为进料溢流管，其下出口距上床层分布板75 mm。三根溢流管的内径均为24 mm。

图1 多层流化床模型结构Fig.1 The structure of the multi-stage fluidized bed

如图2 所示，采用结构化网格对多层流化床模型进行网格划分，经过网格平滑处理后，所有网格质量均在0.5 以上，模型总网格数为432 309。曾尝试使用网格数量为80 万的网格进行模拟，发现所得流化床层压降与本模型无显著区别，因此采用网格数为43 万的模型进行模拟。

图2 多层流化床模型网格Fig.2 The grid of the multi-stage fluidized bed

2 气固两相流动模型

2.1 基本方程

气固两相流的连续性方程如下：

式中：t为时间，s；下标g，s 分别为气相和颗粒相；α为对应相体积分率；ρ为对应相的密度，kg/m3；为对应相的速度，m/s。

各相的动量守恒方程如下：

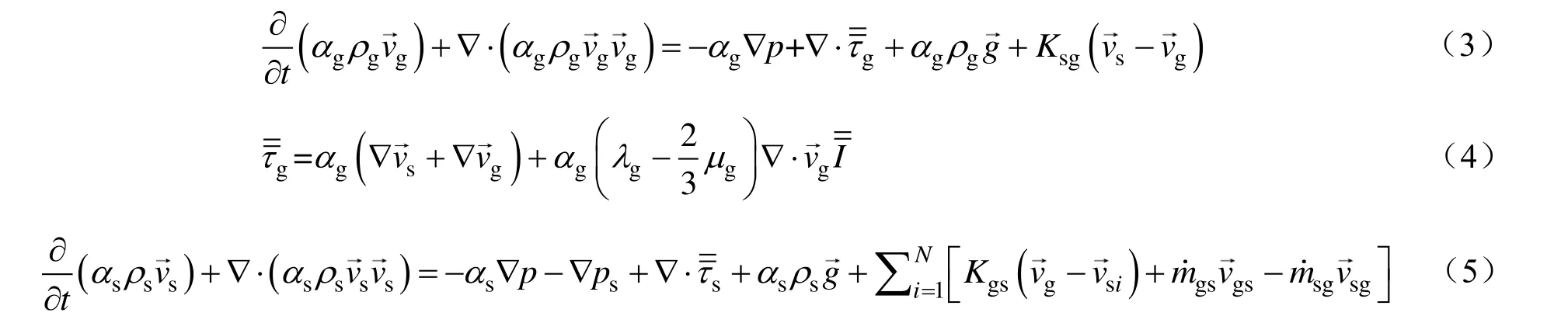
固相压力由方程（7）计算：

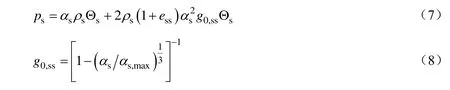
式中：Θs为颗粒温度，K，由基于颗粒动理论的模型进行计算；ess为颗粒碰撞的恢复系数（默认值0.9）；g0,ss为径向分布方程，用于控制颗粒从“可压缩”状态到“不可压缩”状态的转变。

固相体积黏度由Lun 等[8]提出的方程（9）计算：

固相剪切黏度（μs）主要由三部分构成，分别为碰撞部分黏度（μs,col）、动力黏度（μs,kin）和摩擦黏度（μs,fr）：

式中：ds为颗粒直径，m；φ为内摩擦角，°；I2D为偏应力张量的第二恒量，Pa。

颗粒温度由基于颗粒动理论的式（14）计算[9]：

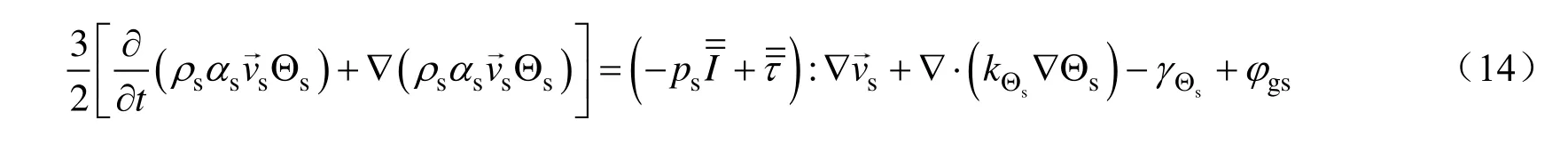
采用Ding 等[10]提出的模型计算相间动量交换系数（Ksg）。Gidaspow 模型主要基于Wen-Yu 模型和Eulerian 模型，在气固流化床的颗粒密相流中有较好的适用性[11-13]。当气相体积分率（αg）大于0.8时，相间动量交换系数由Wen-Yu 模型[13]确定：

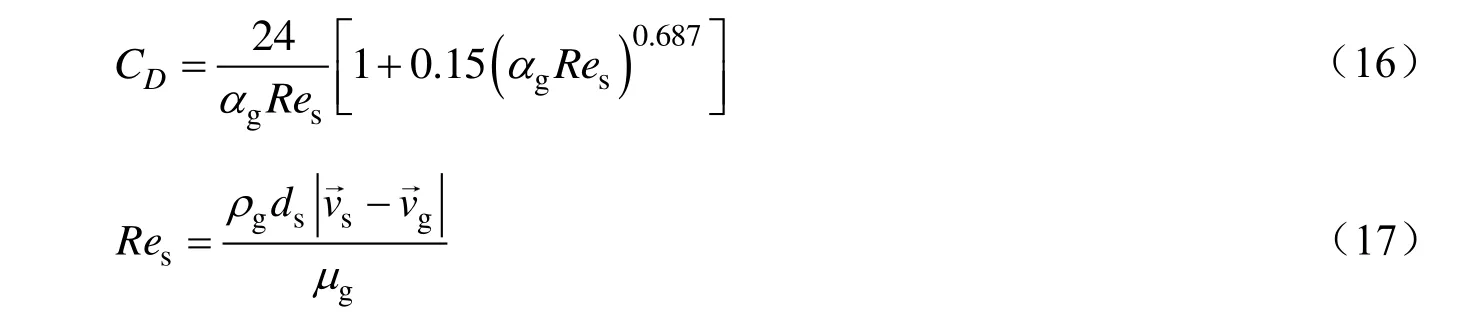
式中：CD为单颗粒曳力系数；Re为颗粒雷诺数。否则，则用Eulerian 模型[15]确定：

2.2 边界条件和初始条件

设置流化气入口为速度进口；设置上床层顶部为压力出口，出口压力即为标准大气压；设置进料溢流管的顶部为速度进口，作为固相颗粒入口；设立出料溢流管底部为压力出口，作为固相颗粒出口，出口压力根据下床层压降确定，为保证该出口无气体回流，出口压力应稍低于下床层压降。

为准确模拟多层流化床上下床层之间的分布板，将上下床层中间的30 mm 区域设置为多孔介质区，通过调节惯性损失系数调节多孔介质区压降，以模拟流化气通过分布板压降。设置初始条件时，下床层的填料静床高为100 mm，床层空隙率为0.5；上床层的填料静床高为70 mm，床层空隙率为0.5；层间传递溢流管（溢流管2）内的填料静床高为250 mm（包括下床层高度），床层空隙率为0.5，以防止窜气。计算时间步长为0.000 5 s，采用Intel Xeon E5-2640 处理器进行8 线程并行计算。

模拟颗粒为硫酸钙颗粒，颗粒密度为2 610 kg/m3，粒径为100 μm。采用的气体是空气，密度为1.225 kg/m3。模拟中采用的多孔区惯性阻力系数为6 000，颗粒速度为0.05 m/s，进料组成中固相体积分数为50%。

3 结果与讨论

3.1 模拟方法的验证

图3 为多层流化床内平均压降的轴向分布，其中平均压降（ΔP）为多层流化床内各床层进出口达到动态平衡后，再稳定计算10 s，提取其中200 个算例（每个间隔0.05 s）数据取平均得到，后续的平均数据均通过此方法获得。

图3 多层流化床内的平均压降轴向分布（时间平均）Fig.3 The axial distribution of time-averaged pressure drop in the multi-stage fluidized bed

如图3（a）所示，多层流化床各床层压降随高度变化呈现典型的阶段性，与郭慕孙等[16]提到的多层流化床内的压力场是相符的。如图3（b）所示，多层流化床溢流管内压降变化也呈现多段性，但与多层流化床主体床层存在明显差别。首先，在下层床区域（0～75 mm）床层压降的变化与图3（a）基本一致；当进入溢流管后，由于溢流管内存在更高的颗粒料位，因此溢流管区域的压力线性下降段更长，直至约200 mm 处结束，可将溢流管内这段压降变化趋势与下床层一致的区域称为溢流管内颗粒密相区（75～200 mm）；在颗粒密相区上方，存在压降逐渐减小，但趋势相较更缓的区域，形成了溢流管内的颗粒稀相区（200～740 mm）；溢流管上口以上部分即为无颗粒相的上层床空间，此时压降随高度升高基本不变，与图3（a）相同。这种变化趋势与文献报道[16]的溢流管内的压力场也十分接近，主要区别在于文献报道溢流管内颗粒稀相区内无压降变化，而模拟结果显示，在这段区域仍存在一定的压降。

在该算例的计算条件下，统计得到的上下床层压降为604.8 Pa 和746.5 Pa，而上下床层的床层持料量分别为2.75 kg 和3.47 kg，由此计算理论压降分别为596.3 Pa 和752.5 Pa，与模拟得到的床层压降一致，定量验证了本模拟的正确性。

3.2 气固流动模式

图4 为多层流化床内固相颗粒的流动模式，图中黑色箭头表示颗粒的流动方向。如图4（a）所示，固相颗粒流入溢流管后，逐渐向下流动进入下床层。由于溢流管内颗粒床层的缓冲作用降低了颗粒流速，进入下床层的颗粒在流化气的作用下向四周分散并与其它颗粒充分混合。在下床层的另一侧，部分流化颗粒从出料溢流管离开下床层。对整个下床层，颗粒的流入与流出同时存在，两者达到动态平衡，从而保证了下床层颗粒料位的稳定。如图4（b），由于进料溢流管内无颗粒床层，进料颗粒以更高的初速度进入上流化床层，无法被迅速分散而向下运动，直至接触到上分布板形成固相堆积区域。另一侧，部分流化颗粒进入层间传递溢流管上口，随后于溢流管内向下流动。

图4 多层流化床内固相流动模式Fig.4 The flow pattern of solid phase in the multi-stage fluidized bed

图5 为多层流化床上下两床层的气相流动模式，图中颜色差异代表该区域的流化气速大小，黑色箭头代表流化气的流动方向。如图5（a），流化气在下流化床层中分布较均匀，无明显气泡涡出现，保证了流化床层的整体均匀性。层间传递溢流管正下方的流化气在向上运动过程中，受下行颗粒影响，只有少部分气流进入溢流管中，其余气体则向四周逸散，从溢流管外部脱离流化床层，而进入溢流管的部分气体也会在下行颗粒的影响下再次返回下层床。如图5（b）所示，上流化床层进料溢流管一侧，由于颗粒下料形成的固相堆积阻碍了溢流管下方流化气进入，使得流化气趋向于向溢流管两侧进入上流化床。在另一侧层间溢流管上方进口附近，部分气流随固体从上床层窜入溢流管，但部分气流又从溢流管内流出。

图5 多层流化床内气相流动模式Fig.5 The flow pattern of gas phase in the multi-stage fluidized bed

对多层流化床层间传递溢流管内的气体流动模式，可以参照图5。在溢流管底部，由于颗粒床层的存在，气体分布整体更接近下流化床层；而在溢流管的上半部，存在两股流速较大、方向相反的气流（为便于下文描述，将向下运动的气流命名为下降气流，主要为从溢流管上进口涌入的流化气；将向上运动的气流命名为上升气流，主要由从溢流管下出口流入的流化气和折返的下降气流组成）。由图5 可发现，溢流管内颗粒料位的存在，阻碍了下降气流进一步向下流入下流化床层，也对从下床层进入溢流管的流化气起到阻挡作用，使溢流管内的颗粒流动状态保持稳定。

3.3 固相体积分布

模拟得到的下流化床层不同高度（h）的固相体积分率及其时域标准差的径向（r）分布如图6 所示。如图6（a）所示，多层流化床下床层固相体积分率在轴向和径向上的分布均较为均匀。由于径向位置为-0.06 m 处位于层间传递溢流管正下方，受颗粒下行进料影响，该处固体体积分率较其它位置偏高。径向位置为0.06 m 时处于出料溢流管内部，固体体积分率接近于0。

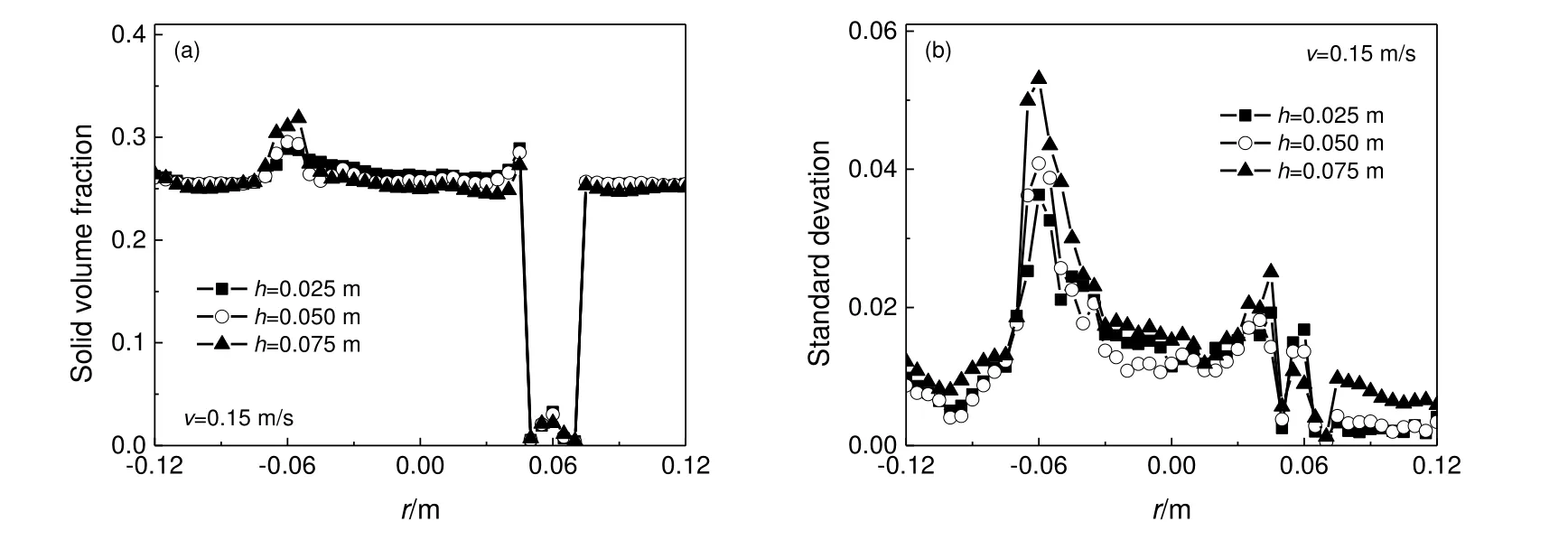
图6 多层流化床下流化床层固相体积分率的径向分布（a）及其时域标准差（b）Fig.6 The radial distribution of solid volume fraction (a) and its time-averaged relative standard deviation (b)in the lower bed of the multi-stage fluidized bed

如图6（b）所示，由于多层流化床的下流化床层层间传递溢流管下方区域存在颗粒下行分散，因此固相体积分率波动最为频繁，该区域内的固相体积分率时域标准差出现极大值。随着高度降低，标准差极大值逐渐减小，下行颗粒逐渐向四周分散进而使固相体积分率趋于稳定。此外，发现流化床层两侧的标准差较中间区域更低，这可能是壁效应的影响。

图7 为多层流化床上流化床层固相体积分率及其标准差的径向分布。如图7（a）所示，相比下流化床层，上流化床层的固相体积分率在轴向和径向上更不稳定。受进料颗粒沉底影响，随着高度增加，固相体积分率逐渐减小。径向位置为-0.06 m 时处于层间传递溢流管内部，固相体积分率接近于0。

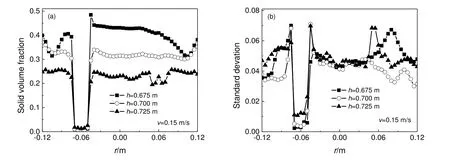
图7 多层流化床上流化床层固相体积分率的径向分布（a）及其时域标准差（b）Fig.7 The radial distribution of solid volume fraction (a) and its time-averaged standard deviation (b)in the upper bed of the multi-stage fluidized bed

如图7（b）所示，上流化床层的标准差相比下床层整体偏大，上流化床层的固相体积分率波动更剧烈。由于上流化床层的流化气趋向于从堆积颗粒的两侧分散颗粒，使这两个区域的固相体积分率波动最为频繁，因此固相体积分率标准差极大值出现在溢流管的两侧。在左侧溢流管区，由于溢流管内部为稀相区，因此标准差极小。

3.4 流化气速的影响

流化气速是多层流化床最重要的操作参数，与床层流化质量、颗粒层间传递稳定性等有着密不可分的关系，因此，研究流化气速对多层流化床内气固相互作用的影响十分必要。在模拟过程中，所有条件均在保证床层进出料平衡后，再连续模拟10 s，每隔0.05 s 保存一次数据并进行分析。图8 所示为不同流化气速时多层流化床中心处（a）和溢流管中心处（b）的平均压降随高度变化的模拟结果。如图8（a）所示，各流化气速下多层流化床床层压降的变化趋势类似，但气速增大时，压降曲线归零点延长，上床层的床层高度增大。如图8（b）所示，各流化气速下溢流管内的压降变化趋势也类似，但气速增大，出现了第三段斜率较陡的压降曲线。

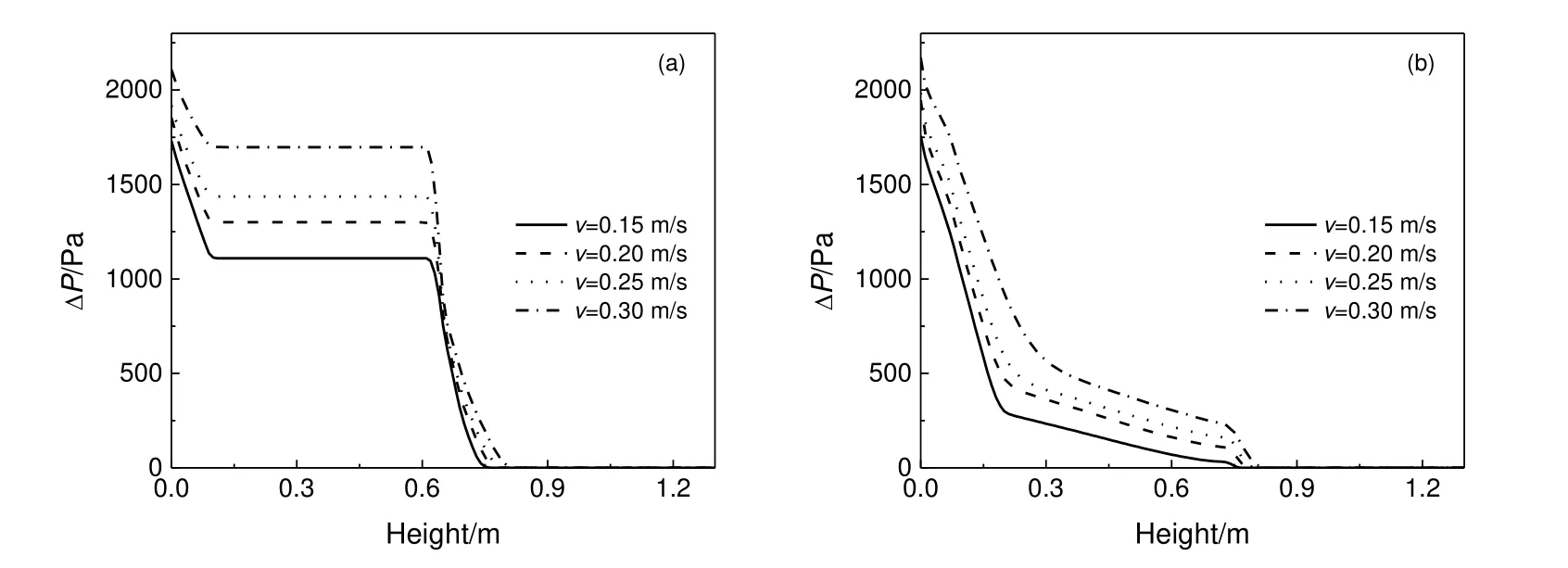
图8 不同流化气速下多层流化床不同位置的时均压降Fig.8 Time-averaged pressure drop distributions in the multi-stage fluidized bed under different gas velocities

图9 为多层流化床床层总压降随流化气速的变化。如图9 所示，流化气速增大，多层流化床上分布板压降增大，且增大趋势符合分布板压降随气速变化的经验公式，说明模拟具有一定的准确性。随着流化气速增大，下床层的压降显著减小，上层床压降先减小后增大。

图9 不同流化气速下的多层流化床床层压降Fig.9 The pressure drops of the multi-stage fluidized bed under different gas velocities

进一步模拟了流化气速对床层固相分布的影响，结果如图10 所示。由图10 可知，流化气速增大，多层流化床下床层高度基本不变，而上层床高度增大。对多层流化床溢流管，随着流化气速的增大，溢流管内颗粒料位高度增加，且溢流管固相区内出现明显的气泡行为。较高气速（0.30 m/s）下，溢流管固相区内甚至观测到一些明显的气相聚集区，表明进一步提高气速，溢流管中的颗粒溢流会出现节涌或喷料，随之失稳。为定量比较各气速下上下床层固相体积分率变化，对不同气速下床层固相体积分率的径向分布进行了分析，如图11 所示。

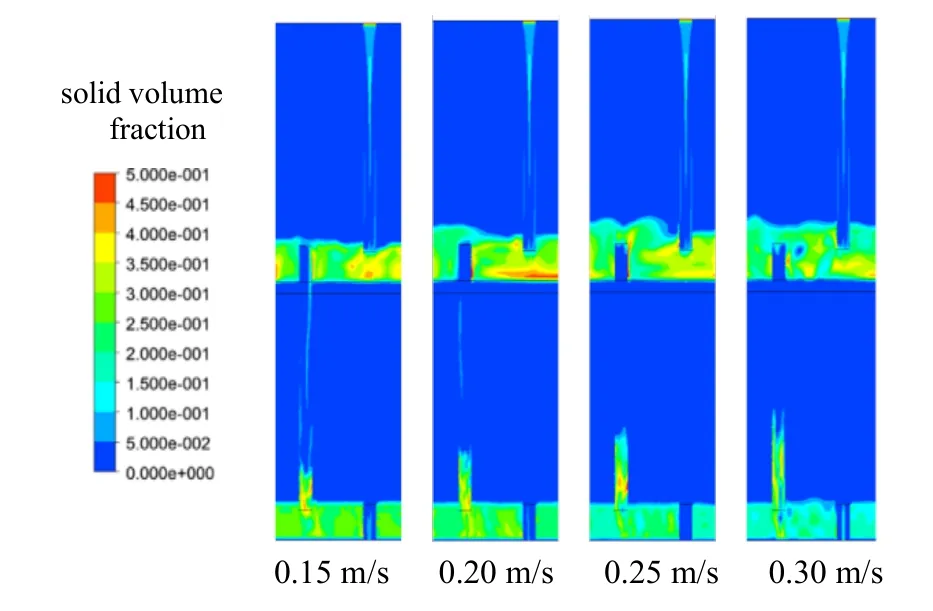
图10 不同气速下多层流化床的整床层固相分布Fig.10 The distributions of solid volume fraction in the multi-stage fluidized bed under different gas velocities

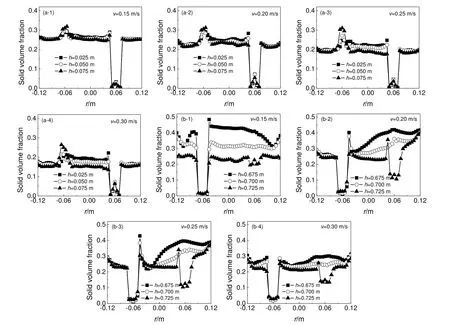
图11 不同流化气速下多层流化床床层固相体积分率分布Fig.11 The distributions of time-averaged solid volume fraction in the multi-stage fluidized bed under different gas velocities(a) lower bed;(b) upper bed

如图11（a）所示，任一气速下下床层固相体积分率的径向分布是均匀的，但气速增大会导致不同高度下床层固相体积分率的径向分布曲线开始逐渐分离，说明流化气速增大，下床层的轴向均匀程度变差；此外，下床层的床层固相体积分率随流化气速的增大而减小。如图11（b）所示，流化气速增大，上床层固相体积分率的径向分布均匀性先变差后又变好；且流化气速增大，不同高度的床层固相体积分率的径向分布曲线逐渐接近且整体下移，表明上床层轴向的固相均匀程度变好，床层固相体积分率减小。

进一步对比不同气速下多层流化床溢流管内平均固相体积分率的轴向分布，结果如图12 所示。可以发现，不同气速下平均固相体积分率的轴向分布都呈现三段式变化。在溢流管底部，由于颗粒床层始终存在，固相体积分率基本不变或缓慢减小，该区域可称为溢流管内的密相区；在溢流管中上部，由于基本无颗粒存在，该区域可称为溢流管内的稀相区；在密相区和稀相区间，存在固相体积分率逐渐下降的过渡区，该区域的大小代表颗粒床层的料位波动范围。随着气速增大，溢流管密相区内固相体积分率逐渐减小，且减小趋势变大，过渡区域的长度则逐渐变长。表明气速增大使溢流管内颗粒床层的稳定性下降，床层料位波动范围变大。当流化气速为0.30 m/s 时，密相区和过渡区的界限开始模糊，溢流管内的颗粒床层整体趋于不稳定，已接近稳定下料的极限。

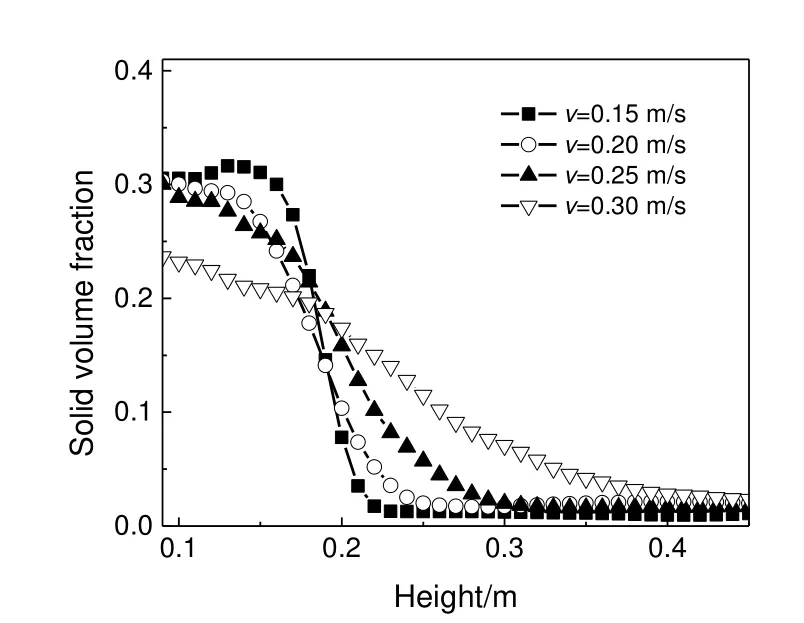
图12 不同气速下溢流管内平均固相体积分率的轴向分布Fig.12 The axial distributions of solid volume fraction in the downcomer under different gas velocities

此外，溢流管的进料是在重力和气体流场的共同作用下间歇进行的，如图13 所示。由于层间传递溢流管内同时存在流速较大、方向相反的上升气流和下降气流，当溢流管内上升气流占主导时，上升气流从溢流管上口涌出，阻挡颗粒进入溢流管中（如图13 中t为0.05～0.20 s 所示）；当溢流管内下降气流占主导时，气流从溢流管上进口涌入，将部分上床层颗粒携带进溢流管并向下运动（如图13 中t为0.25～0.40 s 所示）；当上升气流再次占据主导时，颗粒进料再次受阻（如图13 中t为0.45～0.50 s 所示）。多层流化床运行时，此类间歇过程呈周期性或类周期性发生，总体上保证了颗粒层间传递的持续进行。

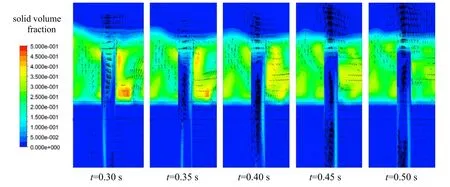
图13 从上床层到层间溢流管入口的非连续进料Fig.13 The non-continuous solid flow from the upper bed to the downcomer

在该过程中，可将颗粒自重和下降气流的携带作用看作层间传递的推动力，将上升气流的阻碍看作阻力。随着流化气速的增大，从溢流管底部出口（下层床中）进入溢流管的气体流量增大，层间传递阻力增大，但对溢流管上部进口（上层床中）进入的下降气流的影响有限，为保证流化床内层间传递得以持续进行，只能依靠溢流管上进口上方的料位积累以提供足够的重力作为层间传递推动力。因此，当流化气速增大时，溢流管上出口附近的床层料位积累量增大（如图14 所示），同步增大了上床层料位高度。

图14 不同气速下溢流管进口上方的固相体积分率Fig.14 The solid volume fraction above the upper outlet of downcomer under different gas velocities

4 结论

使用多孔介质模型模拟两床层间的气体分布板，开发了多层流化床典型结构单元的CFD 模拟方法。在此基础上研究了稳态条件下，多层流化床上下床层及溢流管内的气固相流动行为，得到如下结论：

a）对比多层流化床的上下床层，由于进料颗粒初始状态的差异，下床层固相体积分率在轴向和径向的分布均匀性优于上床层。

b）随着流化气速的增大，多层流化床下床层固相体积分布的轴向均匀性变差，而上床层则相反；溢流管内的密相区浓度降低、浓度梯度增大，密相区与稀相区之间的过渡区域增大。

c）在气固流场和重力的作用下，上流化床层颗粒向溢流管的溢流间歇发生。当溢流管内的上升气流控制时，颗粒向溢流管的溢流被阻挡；当下降气流和重力控制时，颗粒被气流携带进溢流管完成进料。随流化气速的增大，短路进入溢流管的气体量增加，上升气流的阻挡作用增强，为平衡该作用，溢流管上方出现料位积累，上床层高度升高。