斜群代数的倾斜维数
姚海楼,吕鑫龙
(北京工业大学理学部数学学院,北京 100124)
斜群代数最早与文献[1]中奇点的研究有着密不可分的联系. Reiten等[2]对斜群代数做了系统且全面的总结,这使得斜群代数的表示理论初露端倪并且逐渐成为研究热点. 目前,斜群代数已成为代数表示论研究领域中的重要课题之一[3-5].
倾斜理论最早是由英国数学家Brenner等[6]提出并加以发展的. Miyashita等[7]定义了具有有限投射维数的倾斜模,并且讨论了其基本的性质. 结合余代数的研究方法,Wang[8]定义了余代数的倾斜余模,详细讨论了倾斜内射余模和倾斜内射维数. 受此启发,在Artin代数上引入倾斜投射模和倾斜投射维数的概念,并研究其性质. 还研究了ArtinR-代数Λ和斜群代数ΛG的倾斜整体维数之间的关系.
设Λ是一个ArtinR-代数,G是一个有限群,ΛG是一个斜群代数. 本文利用斜群代数和倾斜模的性质,研究斜群代数的倾斜维数. 证明了Λ-模X的倾斜投射维数与ΛG-模ΛG⊗ΛX的倾斜投射维数相等; 进一步,证明了ArtinR-代数Λ的倾斜整体维数和斜群代数ΛG的倾斜整体维数相等.
1 预备知识
设R为Artin交换环,
定义1[9]设G是有限群,G在Λ上的R-代数作用是满足下列条件的函数G×Λ→Λ.
1) 对所有σ∈G,σ∶Λ→Λ是R-代数的自同构.
2) (σ1σ2)(λ)=σ1(σ2(λ)),σ1,σ2∈G,λ∈Λ.
3) 1λ=λ,λ∈Λ,1是G的恒等元.
定义2[9]设G是一个有限群,Λ为ArtinR-代数,且G×Λ→Λ是G在Λ上的R-代数作用,则G在Λ上的斜群代数(记为ΛG)由下列条件给出.
1)ΛG作为Abel群是以G的元素为基的自由左Λ-模.
2)ΛG上的乘法定义为(λσσ)(λττ)=(λσσ(λτ))στ,λσ,λτ∈Λ,σ,τ∈G.
命题1[9]设ΛG是斜群代数且G的阶|G|为n,则
1) 若n在Λ中可逆,则平凡ΛG-模Λ是一个投射模.
2) 若G平凡的作用在Λ上,即对任σ∈G和λ∈Λ有σλ=λ,则Λ是投射ΛG-模当且仅当n在Λ中可逆.
引理1[9]设Λ是ArtinR-代数,G为有限群,ΛG为斜群代数,则
1) 群G⊂ΛG是ΛG的一个基,其中ΛG是作为左和右Λ-模.
命题2[9]令Λ是R-代数Γ的子代数,且满足如下条件,则有gl.dim(Γ)≥gl.dim(Λ).
1)Γ是投射左Λ-模.
2) 存在Γ的一个子群C,C是Γ的一个Λ-子双模,使得Γ=ΛЦC.
推论1[9]设ΛG为斜群代数,则gl.dim(Λ)≤gl.dim(ΛG).
引理2[9]设ΛG是斜群代数且G的阶|G|在Λ中可逆. 若Y是任意ΛG-模,则Y是AG⊗ΛY的直和加项.
命题3[9]设Λ是ArtinR-代数Γ的R-子代数,且满足如下条件,则gl.dim(Γ)≤gl.dim(Λ).
1)Γ是投射右Λ-模.
2) 每一个Γ-模Y同构于Γ⊗ΛY的一个直和项.
推论2[9]令ΛG是斜群R-代数,且G的阶|G|在Λ中可逆. 则gl.dim(Λ)≥gl.dim(ΛG).
由推论1和推论2可立刻得到如下定理:
定理1[9]令ΛG是斜群R-代数,且G的阶|G|在Λ中可逆,则gl.dim(Λ)=gl.dim(ΛG).
命题4[9]令Λ是ArtinR-代数Γ的R-子代数. 则下面2条叙述是等价的.
1) 从modΛ到modΛG的函子HomΛ(Γ,-)与函子Γ⊗Λ-是自然同构的.
2) 下面的条件均是成立的.
①Γ是投射左Λ-模.
②Γ和HomΛ(Γ,Λ)作为Γ-Λ-双模是同构的.
命题5[9]令ΛG是斜群代数,则从modΛ到modΛG的函子ΛG⊗Λ-和函子HomΛ(ΛG,-)是自然同构的.
定理2[10](相伴性定理) 假设R和S是2个环,M是一个(R,S)-模,即左S右R-模,E是左S-模,A是左R-模. 则有群同构
ω∶HomR(A,HomS(M,E))→
HomS(M⊗RA,E),φ→f
φ(a)(m)=f(m⊗a)∈E
定义3[11]设A为代数,A-模T称为偏倾斜模,如果T满足条件
1) proj.dim(TA)≤1.
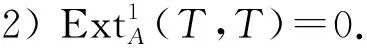
定义4[11]偏倾斜模T称为倾斜模,若它还满足条件
3) 存在下述的一个短正合列
0→AA→T′A→T″A→0
式中T′,T″∈addT,其中addT是由有限多个T的直和的直和加项构成的模类.
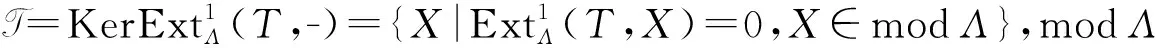
注1[11]T关于模的同态像,直和及扩张是封闭的.
定义6令M是一个Λ-模. 定义M的倾斜投射维数为
t.proj.dim(M)=
inf{n|0→En→…→E1→E0→M→0}
其中0→En→…→E1→E0→M→0是M的一个倾斜投射分解,且所有的Ei是倾斜投射Λ-模. 若不存在这样的n,则称M的倾斜投射维数为无穷的,记为t.proj.dim(M)=∞.
定义7令M是右Λ-模. 定义ArtinR-代数Λ的右倾斜整体维数
t.rgl.dim(Λ)=sup{t.proj.dim(M)|M∈modΛ}
以同样的方式,也可定义ArtinR-代数的左倾斜整体维数.
2 主要结果
首先,有倾斜投射模的等价条件的命题.
命题1对一个模M,下列叙述等价.
1)M是倾斜投射的.
3) 对任何形如下述的短正合列
其中N1∈T,和任何的模同态f∶M→N2,存在一个模同态g∶M→N,使得h∘g=f.
4) 如果N∈T,则任何形如下述的短正合列
0→N→E→M→0
是可裂的.
证明: 1)⟹2)对任何的L∈T,存在一个短正合列
0→L→I→N→0
(1)
式中I是内射的.
因M是倾斜投射的,应用函子HomΛ(M,-),则有长正合列
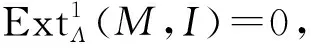
应用函子HomΛ(T,-)于短正合列(1),得如下长正合列
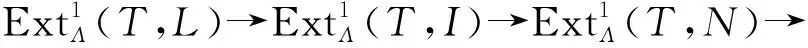
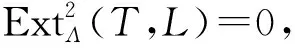
于是,短正合列(1)为T中的短正合列. 又因函子HomΛ(M,-)保持T中序列的正合性,故有正合列
0→HomΛ(M,L)→HomΛ(M,I)
→HomΛ(M,N)→0
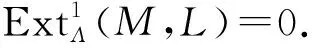
2)⟹3) 对任意的下述短正合列
式中N1∈T,和任何模同态f∶M→N2,应用函子HomΛ(M,-),可得下述长正合列
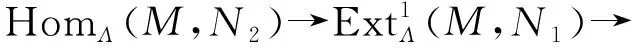
0→HomΛ(M,N1)→HomΛ(M,N)
→HomΛ(M,N2)→0
因此,对任何的模同态f∶M→N2,存在一个模同态g∶M→N,使得h∘g=f.
3)⟹4) 对任意的短正合列
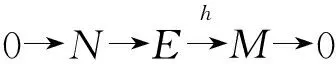
因N∈T,对恒等同态1M∶M→M,由3)知,存在一个模同态g∶M→E使得h∘g=1M. 因此该短正合列是右可裂的,从而是可裂的.
4)⟹1) 取T中的短正合列
0→A→B→C→0
应用函子HomΛ(M,-),可得下述长正合列
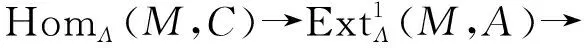
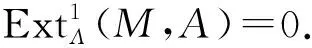
0→HomΛ(M,A)→HomΛ(M,B)→
HomΛ(M,C)→0
由倾斜投射模定义可知,M是倾斜投射的.
定理1令X是Λ上的倾斜模,则ΛG⊗ΛX是ΛG上的倾斜模.
证明: 首先,因为X是Λ上的倾斜模,于是有proj.dim(X)≤1,从而得到X的投射分解
0→P1→P0→X→0
(2)
式中P1、P0是投射Λ-模. 由预备知识中的命题2、3,推论1、2及定理1可知,ΛG作为左和右Λ-模都是投射的,于是得到ΛG⊗ΛX的投射分解
0→ΛG⊗ΛP1→ΛG⊗ΛP0→ΛG⊗ΛX→0
(3)
式中ΛG⊗ΛP1、ΛG⊗ΛP0是投射ΛG-模. 因此得到
proj.dimΛG(ΛG⊗ΛX)≤proj.dim(X)≤1
其次,应用函子HomΛG(-,ΛG⊗ΛX)于短正合列(3)得到长正合列
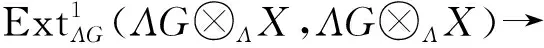
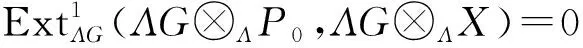
再由预备知识中的定理2可得
HomΛG(ΛG⊗ΛX,ΛG⊗ΛX)≅
HomΛ(X,HomΛG(ΛG,ΛG⊗ΛX))≅
HomΛ(X,ΛG⊗ΛX)
HomΛG(ΛG⊗ΛP0,ΛG⊗ΛX)≅
HomΛ(P0,HomΛG(ΛG,ΛG⊗ΛX))≅
HomΛ(P0,ΛG⊗ΛX)
HomΛG(ΛG⊗ΛP1,ΛG⊗ΛX)≅
HomΛ(P1,HomΛG(ΛG,ΛG⊗ΛX))≅
HomΛ(P1,ΛG⊗ΛX)
应用函子HomΛ(-,ΛG⊗ΛX)于短正合列(2)可得长正合列

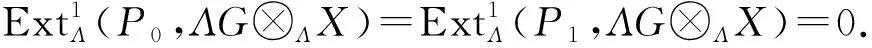
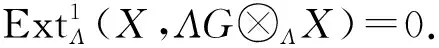
所以,得
因此,函子HomΛ(-,ΛG⊗ΛX)保持短正合列(2)的正合性.
于是,函子HomΛG(-,ΛG⊗ΛX)保持短正合列(3)的正合性,故得如下短正合列
0→HomΛG(ΛG⊗ΛP1,ΛG⊗ΛX)→
HomΛG(ΛG⊗ΛP0,ΛG⊗ΛX)→
HomΛG(ΛG⊗ΛX,ΛG⊗ΛX)→0
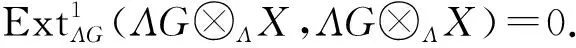
最后,因X是Λ上的倾斜模,则存在短正合列
0→Λ→X′→X″→0
式中X′、X″∈addX. 因ΛG是投射左和右Λ-模,知ΛG⊗Λ-保持序列正合性,故得到短正合列
0→ΛG⊗ΛΛ→ΛG⊗ΛX′→ΛG⊗ΛX″→0
式中ΛG⊗ΛX′和ΛG⊗ΛX″属于addΛG⊗ΛX.
综上所述,ΛG⊗ΛX是ΛG上的倾斜模.
定理2如果X是关于T的倾斜投射模,则ΛG⊗ΛX是关于ΛG⊗ΛT的倾斜投射模.
证明: 因T是倾斜模,由定理1可知ΛG⊗ΛT是倾斜模.
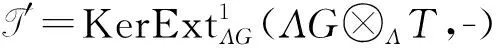
0→A→B→C→0
(4)
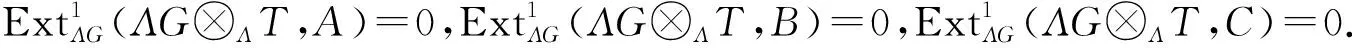
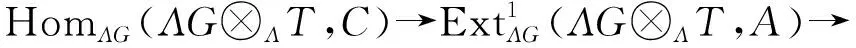
由于A、B、C是ΛG-模,则A、B、C也可以看成是Λ-模. 故短正合列(4)也可看成是Λ-模的短正合列.
于是得
HomΛG(ΛG⊗ΛT,A)≅HomΛ(T,HomΛG(ΛG,A))≅
HomΛ(T,A)
HomΛG(ΛG⊗ΛT,B)≅HomΛ(T,HomΛG(ΛG,B))≅
HomΛ(T,B)
HomΛG(ΛG⊗ΛT,C)≅HomΛ(T,HomΛG(ΛG,C))≅
HomΛ(T,C)
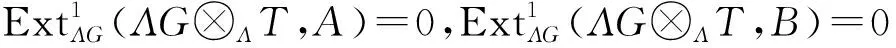
0→HomΛG(ΛG⊗ΛT,A)→HomΛG(ΛG⊗ΛT,B)→
HomΛG(ΛG⊗ΛT,C)→0
从而函子HomΛG(ΛG⊗ΛT,-)保持短正合列(4)的正合性. 将A、B、C看成是Λ-模时,由上述同构关系,有短正合列
0→HomΛ(T,A)→HomΛ(T,B)→HomΛ(T,C)→0故函子HomΛ(T,-)也保持短正合列(4)的正合性. 故A、B、C也属于T.
应用函子HomΛG(ΛG⊗ΛX,-)于短正合列(4),得如下长正合列
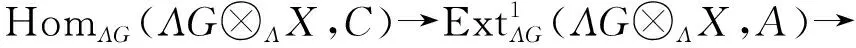
再由预备知识中的定理2可得
HomΛG(ΛG⊗ΛX,A)≅HomΛ(X,HomΛG(ΛG,A))≅
HomΛ(X,A)
HomΛG(ΛG⊗ΛX,B)≅HomΛ(X,HomΛG(ΛG,B))≅
HomΛ(X,B)
HomΛG(ΛG⊗ΛX,C)≅HomΛ(X,HomΛG(ΛG,C))≅
HomΛ(X,C)
因为HomΛ(X,-)在T中保持序列的正合性,故函子HomΛG(ΛG⊗ΛX,-)也保持短正合列(4)的正合性,即HomΛG(ΛG⊗ΛX,-)在T′中保持序列的正合性. 因此,ΛG⊗ΛX是关于ΛG⊗ΛT的倾斜投射模.
定理3对左Λ-模M,下列叙述是等价的
1) t.proj.dim(M)≤n.
2) 如果存在一个正合列
0→X→En-1→…→E1→E0→M→0
其中所有Ei为倾斜投射的,则X是倾斜投射的.
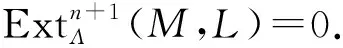
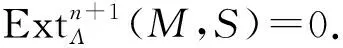
证明: 1)⟹3)对n用归纳法. 若t.proj.dim(M)≤1,则由定义得短正合列
0→E1→E0→M→0
其中E1、E0是倾斜投射的. 应用函子HomΛ(-,L)于上述正合列得
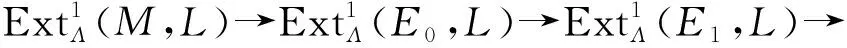
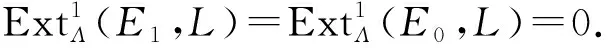
0→L→I→N→0
其中I是内射的. 应用函子HomΛ(M,-)于上述短正合列得
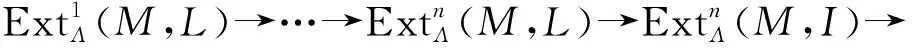
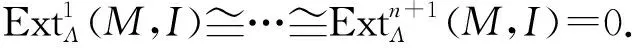
3)⟹2)对任何模L∈T,考虑正合列
其中所有的Ei是倾斜投射的. 于是有短正合列
0→Imd1→E0→M→0
0→X→En-1→Imdn-1→0
0→Imdi+1→Ei→Imdi→0
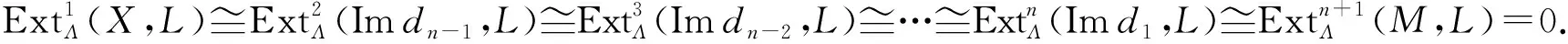
2)⟹1) 假设正合列
0→X→En-1→…→E1→E0→M→0
是M的倾斜投射分解. 由倾斜投射维数的定义立刻得到t.proj.dim(M)≤n.
1)⟹4)与1)⟹3)是类似的.
4)⟹1)令序列
0→X→En-1→…→E1→E0→M→0
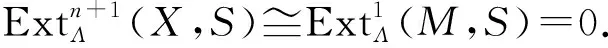
考虑到
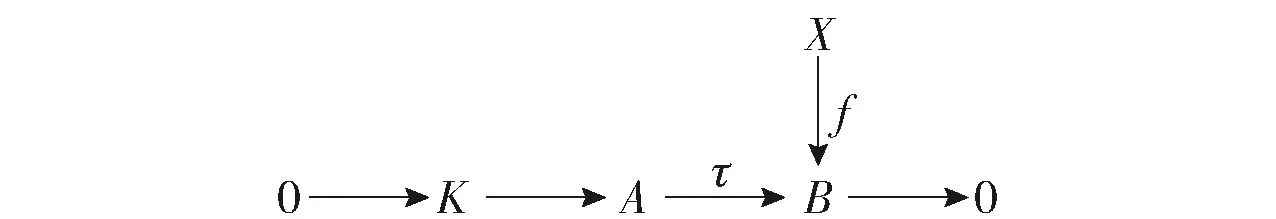
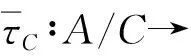
由于K是有限生成的,而Λ是Artin代数,从而为Noether代数,故K是Artin模也是Noether模,即K有合成列.
设C是K的任意子模,则K/C也有合成列,从而K与K/C分别有合成列长度l(K)和l(K/C).
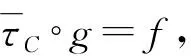
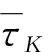
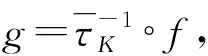
即K∈T,因此Γ≠∅,即Γ为K的一个子模集.
令H={l(K/C)|C∈Γ},则H是非负整数集,并且对任何的C∈Γ,都有l(K/C)≤l(K).
故H中存在最大非负整数n,不妨设Z∈Γ使得l(K/Z)=n.
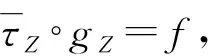
下面分情况1和情况2讨论.
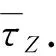
情况2 若Z≠0. 以下再分2种情况讨论.
情况2.1 若Z≠K,则K中存在一个极大子模N使得Z不包含在N中. 事实上,任取0≠z0∈Z,令Ω={Y|Y为K的子模并且z0∈Y}.
因K有合成列,故K满足极大条件. 因此Ω中存在极大的子模Y0.
断言Y0是K的极大子模. 应用反证法. 若Y0不是K的极大子模,则有Y的极大子模Y1包含Y0. 由于Y0在Ω中是极大的可知z0∈Y1,断言Λz0+Y0=K,否则,存在z1∈K使得z1Λz0+Y0,故Λz1+Y0真包含Y0. 这与Y0在Ω是极大的相矛盾,于是Λz0+Y0=K. 由于z0∈Y1并且Y0⊆Y1,因此Y1=K,这与Y1是K的极大子模相矛盾. 所以,Y0是K的极大子模.

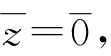
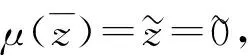
又因为K/Y0为单模,故μ为同构,从而Z/Q为单模,并且Z/Q≅K/Y0∈T. 而Q是Z的极大子模,故有短正合列
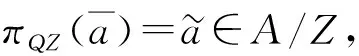
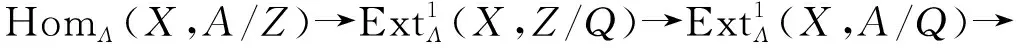
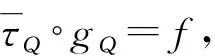
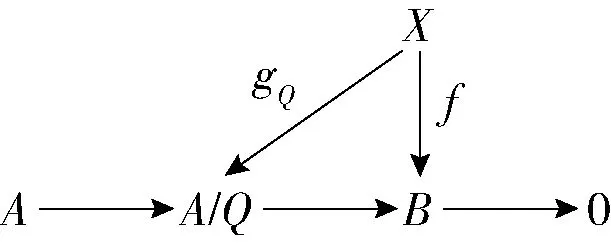
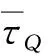
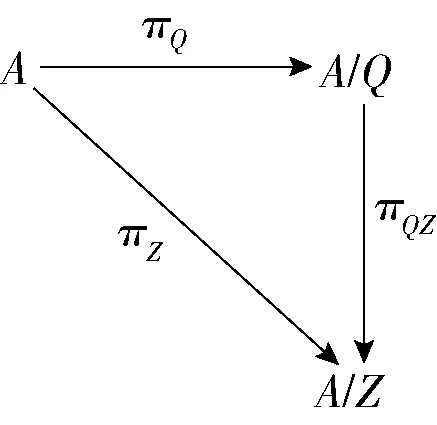
即πQZ∘πQ=πZ,这里πQ与πZ为自然满同态. 显然,有2个交换图
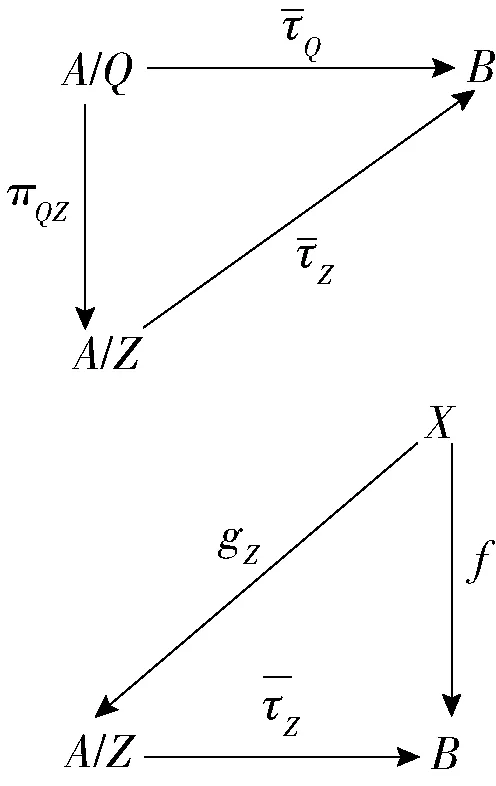
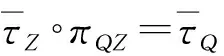
从而Q∈Γ,但l(K/Q)>l(K/Z),这与l(K/Z)是H中的最大数相矛盾. 故情况2.1不能出现.
情况2.2 若Z=K,则K中含有极大子模Q,从而有单模K/Q∈T. 于是有短正合列
应用函子HomΛ(X,-)作于上述短正合列,得
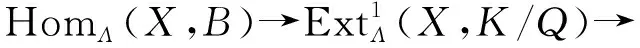
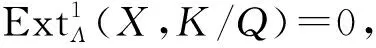
综上,只有情况1成立,即X是倾斜投射模.
注2上述定理对右倾斜模TΛ也是成立的.
定理4令A,B,C是左Λ-模. 若序列
0→A→B→C→0
是正合的,则有如下关系.
1) 如果t.proj.dim(B)>t.proj.dim(A),则有
t.proj.dim(C)=t.proj.dim(B)
2) 如果t.proj.dim(B) t.proj.dim(C)=t.proj.dim(A)+1 3) 如果t.proj.dim(B)=t.proj.dim(A),则有 t.proj.dim(C)≤t.proj.dim(A)+1 证明: 对任何模M∈T,任何n≥0,应用函子HomΛ(-,M),有长正合列 设t.proj.dim(B)=m,t.proj.dim(A)=n. 命题2令A、B、C都是左Λ-模. 如果序列 0→A→B→C→0 是正合的,并且A、B、C中有2个的倾斜投射维数有限,则第3个的倾斜投射维数也必然有限. 定理5令Λ是一个ArtinR-代数,G为有限群,M是左Λ-模. 则有关系 t.proj.dimΛ(M)=t.proj.dimΛG(ΛG⊗ΛM) 证明: 任取M的一个倾斜投射分解, 其中所有的Ei都是倾斜投射左Λ-模,于是得到ΛG⊗ΛM的一个倾斜投射分解 由定理2可知,其中所有的ΛG⊗ΛEi都是倾斜投射左ΛG-模. 若Imdn是倾斜投射Λ-模,则Im(1ΛG⊗dn)是倾斜投射ΛG-模. 因此有 t.proj.dimΛG(ΛG⊗ΛM)≤t.proj.dimΛ(M) 下面取ΛG⊗ΛM的一个倾斜投射分解 0→Fn→…→F1→F0→ΛG⊗ΛM→0 其中所有的Fi都是倾斜投射左ΛG-模,于是Fi作为Λ-模仍是倾斜投射的. 又因为ΛG可分解为n个Λ的直和,其中n=|G|,故有 t.proj.dimΛ(M)≤t.proj.dimΛG(ΛG⊗ΛM) 综上所述,有 t.proj.dimΛ(M)=t.proj.dimΛG(ΛG⊗ΛM) 定理6令ΛG是斜群代数,群G的阶|G|在Λ中可逆,则成立 t.gl.dim(Λ)=t.gl.dim(ΛG) 证明: 首先证明t.gl.dim(Λ)≤t.gl.dim(ΛG). 令X是左Λ-模,则ΛG⊗ΛX是ΛG-模. 下面取ΛG⊗ΛX的极小倾斜投射分解 0→En→…→E1→E0→ΛG⊗ΛX→0 (5) 其中所有的Ei都是倾斜投射的. 因ΛG是投射左Λ-模,故当正合列(5)被视为Λ-模的正合列时,可认为其是ΛG⊗ΛX作为Λ-模时的倾斜投射分解. 因此有 t.proj.dimΛG(ΛG⊗ΛX)≥t.proj.dimΛ(ΛG⊗ΛX) 因为ΛG作为双模同构于Λ⊕C,其中C是ΛG的一个子双模,故ΛG⊗ΛX作为左Λ-模有 ΛG⊗ΛX≅(Λ⊗ΛX)⊕(C⊗ΛX) 因为Λ⊗ΛX≅X,故X是ΛG⊗ΛX的直和加项. 因此,得到 t.proj.dimΛ(X)≤t.proj.dimΛ(ΛG⊗ΛX) 从而 t.proj.dimΛ(X)≤t.proj.dimΛ(ΛG⊗ΛX)≤ 两边取上确界立刻得到 t.gl.dim(Λ)≤t.gl.dim(ΛG) 下面证明t.gl.dim(ΛG)≤t.gl.dim(Λ). 令Y是左ΛG-模. 则将Y视为Λ-模时有Λ-模倾斜投射分解 0→Et→…→E1→E0→Y→0 其中所有的Ei都是关于T的倾斜投射模. 因ΛG是Λ-投射的,故序列 0→ΛG⊗ΛEt→…→ΛG⊗ΛE1→ (6) 是正合的. 再由定理2可知,其中所有的ΛG⊗ΛEi都是关于ΛG⊗ΛT的倾斜投射模. 因此,正合列(6)是ΛG⊗ΛY的一个倾斜投射分解. 于是,有 t.proj.dimΛG(ΛG⊗ΛY)≤t.proj.dimΛ(Y) 再由预备知识中的引理2可知,Y是ΛG⊗ΛY的直和加项. 于是,有 t.proj.dimΛG(Y)≤t.proj.dimΛG(ΛG⊗ΛY) 从而得到 t.proj.dimΛG(Y)≤t.proj.dimΛG(ΛG⊗ΛY)≤ 两边取上确界得 t.gl.dim(ΛG)≤t.gl.dim(Λ) 综上所述,有t.gl.dim(Λ)=t.gl.dim(ΛG). 1) 令A、B、C都是左Λ-模. 如果序列0→A→B→C→0是正合的,并且A、B、C中有2个的倾斜投射维数有限,则第3个的倾斜投射维数也必然有限. 2) 令ΛG是斜群代数,群G的阶|G|在Λ中可逆,则:t.gl.dim(Λ)=t.gl.dim(ΛG).
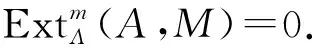
t.proj.dimΛG(ΛG⊗ΛX)
ΛG⊗ΛE0→ΛG⊗ΛY→0
t.proj.dimΛ(Y)3 结论

