基于Fréchet距离函数的轨迹隐私保护方法
张兴兰,杨文金
(1.北京工业大学信息学部,北京 100124; 2.可信计算北京市重点实验室,北京 100124)
随着全球定位系统(global positioning system,GPS)的发展,基于位置服务[1](location based services,LBS)的应用越来越广泛,人们通过这些应用可以发现最近的酒店、超市和医院等,它们正在改变着信息时代人们的生活[2-3]. LBS在服务过程中会产生大量包含用户的会见、位置信息的数据. 人们可以通过对这些数据进行挖掘、分析得到许多有用信息以帮助决策,比如:通过分析某区域内用户的轨迹信息可以发现用户感兴趣的位置,在这些位置建立商业圈,能帮助投资者实现盈利的最大化. 然而,对这些轨迹数据进行分析,也可以推测出用户的生活轨迹、健康状况等隐私信息,如果这些个人隐私信息被泄露会对用户造成极大的威胁[4-8]. 因此,对用户轨迹隐私信息保护技术的研究,已经成为信息安全领域研究的重要内容之一.
Clarke等[9]提出一种能够保护用户的位置隐私和轨迹隐私的方法. 该方法选择了多个特定的合作伙伴来保护用户的位置隐私,并且通过构建在间隔时间内与用户的轨迹类似的多个轨迹来保护用户的轨迹隐私. Abul等[10]提出NWA(never walk alone)方法,该方法基于共定位的(k,δ)-匿名模型,将轨迹集合划分为互不相交的子集,然后通过聚类形成轨迹k-匿名集合. 吴英杰等[11]提出了一种基于聚类杂交的k-匿名隐私保护技术,该方法是针对轨迹等价类特征所提出的,同时考虑了时间和空间对轨迹相似性的影响. Shen等[12]提出了一种以用户为中心的轨迹隐私保护方法以防止轨迹攻击. 他们引入位置语义多样性以最大化轨迹隐私,将攻击和防御问题转化为贝叶斯 Stackelberg 方式以进行定量分析. Gao等[13]提出了一种基于个性化轨迹隐私图模型的隐私保护方法,该方法同时考虑了时间、空间和轨迹方向对轨迹相似性的影响. 文献[10-13]中轨迹k-匿名技术在度量轨迹相似性时均采用欧几里得距离函数,只能度量等长且时间点一一对应的轨迹的距离. 因此,在构造同步轨迹集过程中,不等长轨迹转换等长轨迹时会有较多轨迹首部和尾部的位置点被删除,造成较大信息损失.
这些隐私保护方法一定程度上保护了轨迹隐私,但是均未考虑轨迹的形状,另外,未考虑轨迹的速度. 本文提出一种基于Fréchet 距离函数的轨迹隐私保护方法,在计算轨迹间距离的同时能够考虑轨迹的形状,另外,在轨迹方向相似的基础上考虑轨迹的速度使得轨迹间相似性更高,攻击者识别轨迹的难度增加. 最后,通过轨迹图划分形成轨迹匿名集合.
1 相关概念
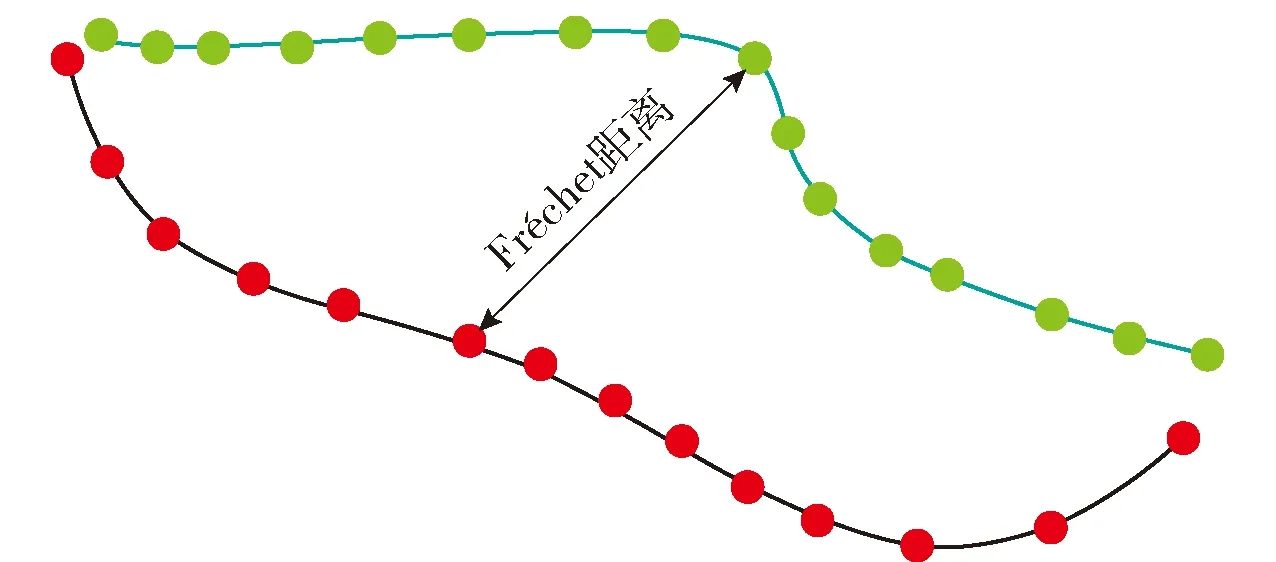
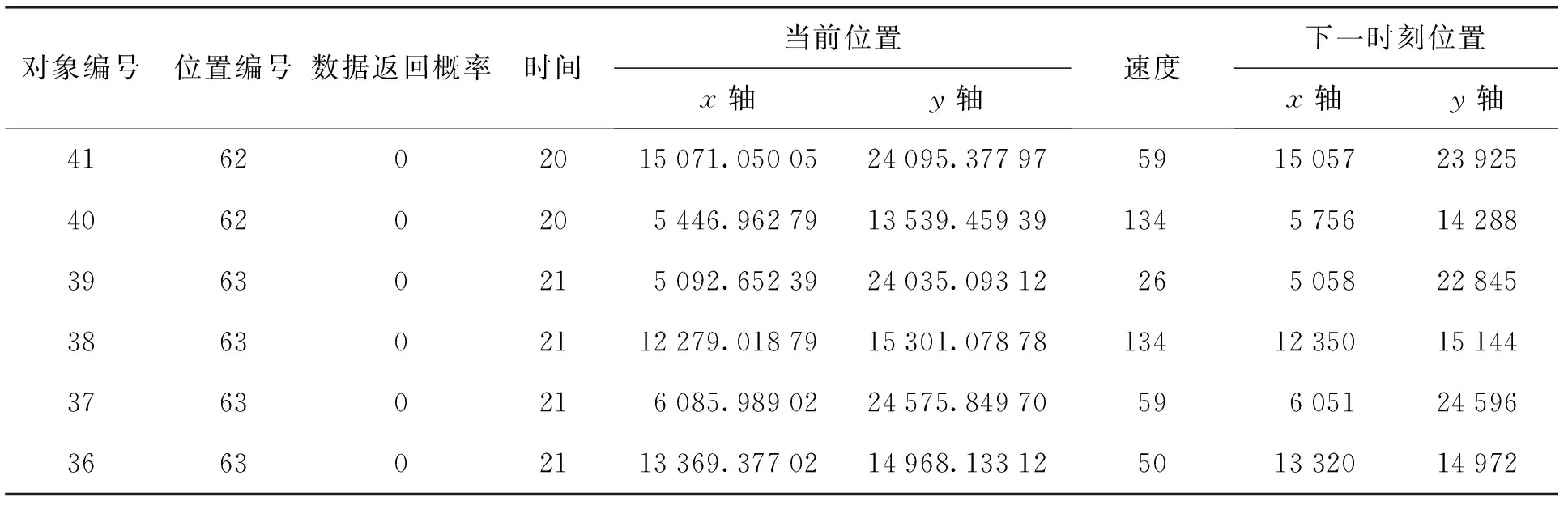
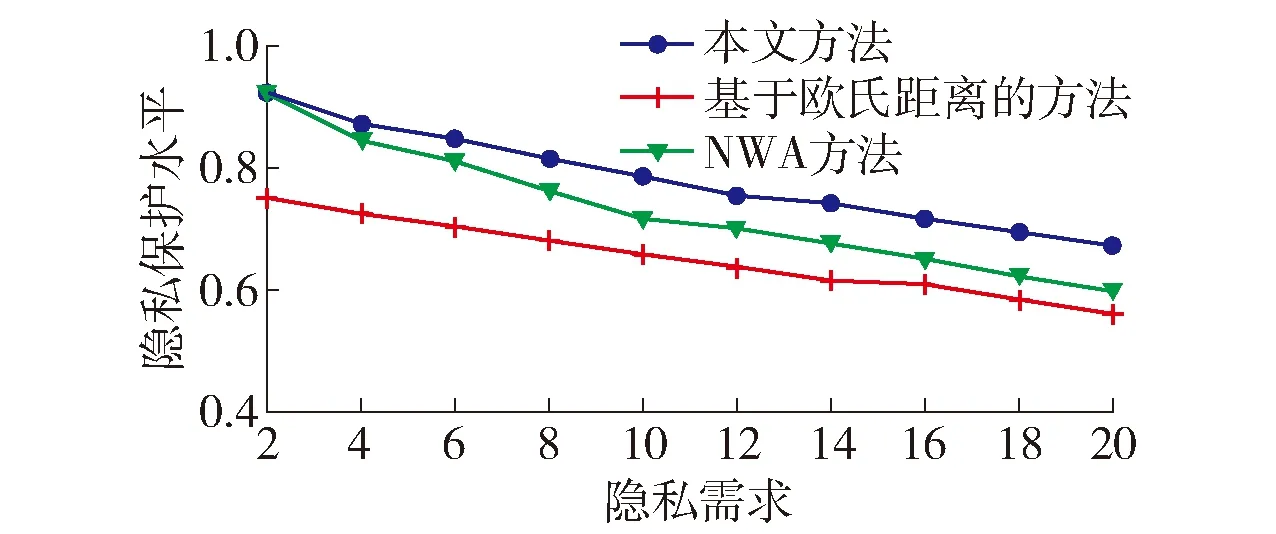
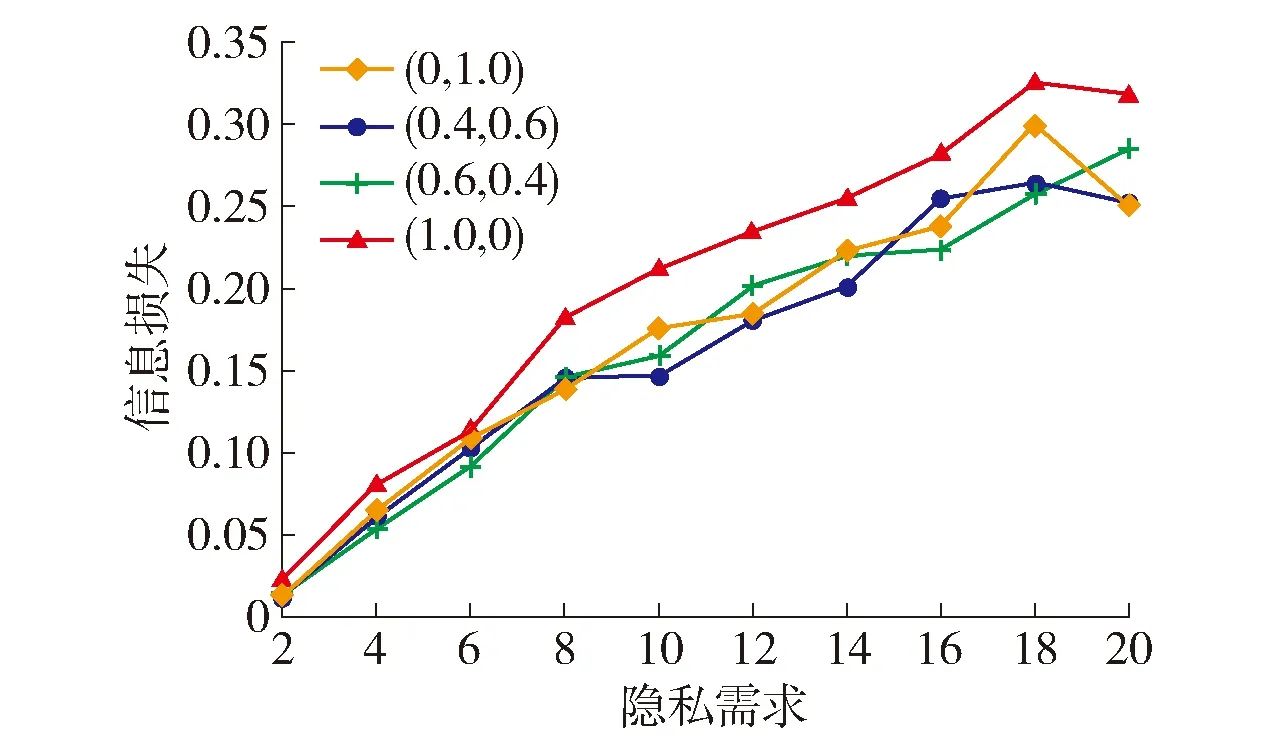
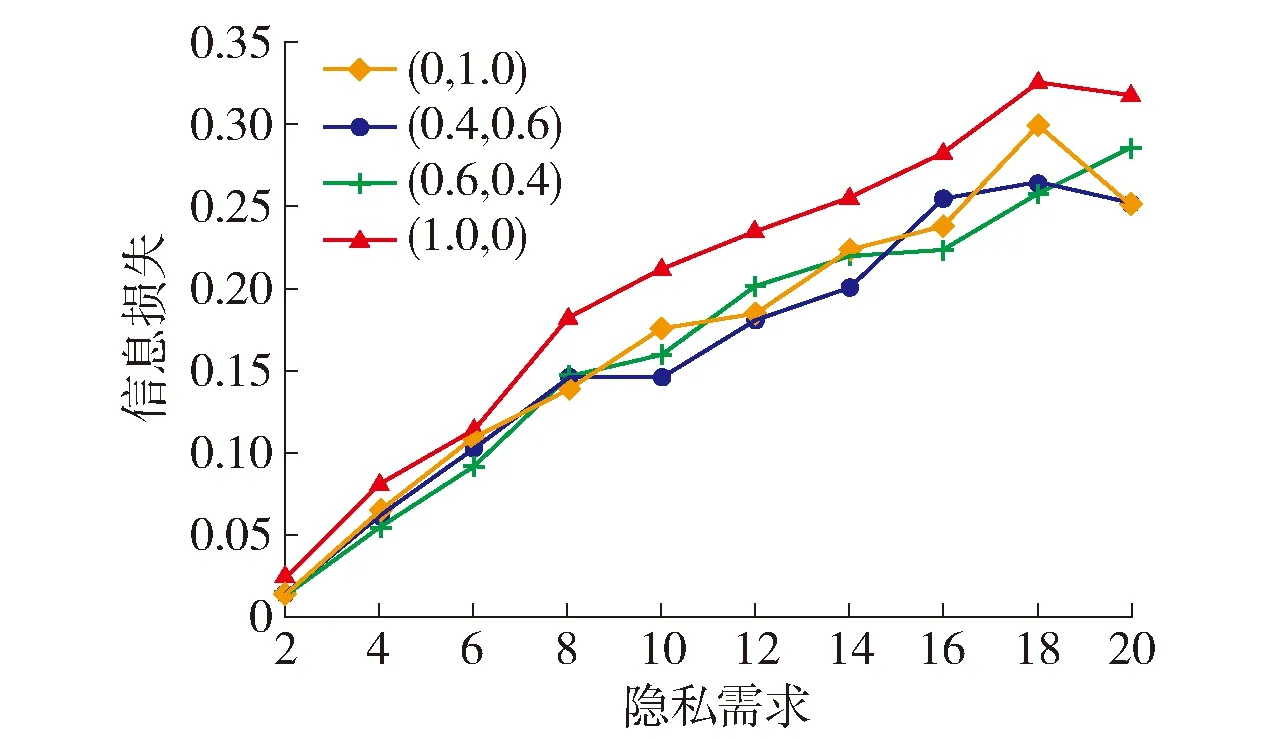
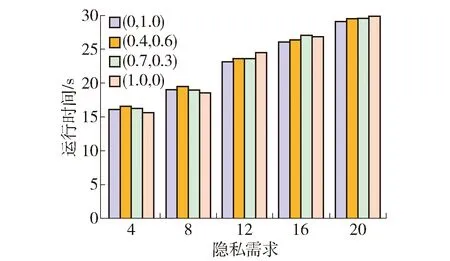
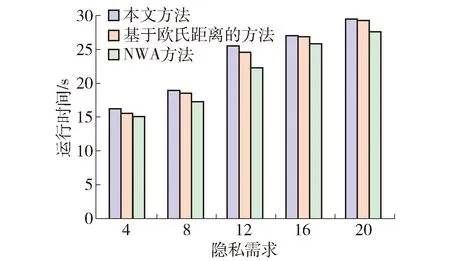
定义1轨迹. 移动对象O的轨迹T为三维时空坐标拟合的曲线,表示为T={Id,(x1,y1,t1,v1),(x2,y2,t2,v2),…,(xm,ym,tm,vm)}. 其中:Id为移动对象的身份标识;(xi,yi)为O在i时刻的位置坐标并且t1 定义2[14]同步轨迹. 2条不同的轨迹Tp和Tq,如果Tp和Tq具有相同的时间序列,那么称Tp和Tq是同步轨迹;如果轨迹集合中的任意2条轨迹两两同步,则称轨迹集合是同步的. 然而,在实际环境中移动对象的轨迹往往不是同步的. 主要有2个原因:一是由于移动终端或GPS对每个移动对象位置的采样时间不同,二是由于不同移动对象向LBS发送请求服务的时间各不相同. 另外,本文在做轨迹处理时,假设轨迹在2个样本时间点内匀速直线运动,对于轨迹Tp和Tq间不同时间坐标,通过在轨迹中插入相应时刻的位置坐标来实现轨迹Tp和Tq的同步. 图1显示了2个同步轨迹. 设二元组(S,d)是一个度量空间,其中d是S上的度量函数. 在单位区间[0,1]上的映射γ:[0,1]→S是连续映射,则称γ为S上的连续曲线. 从单位区间到其自身的映射ζ:[0,1]→[0,1]满足如下3个条件:1)ζ是连续的;2)ζ是非降的,即对于任意x,y∈[0,1]且x≤y,都有ζ(x)≤ζ(y)成立;3)ζ是满射,则称函数ζ为单位区间[0,1]的重参数化函数且此时有ζ(0)=0,ζ(1)=1. 特别地,当ζ为恒等函数ζ(x)=x时,称ζ为平凡重参数化函数,否则,称ζ为非平凡重参数化函数. 显然单位区间的重参数化函数有无穷多个. 设A和B是S上的2条连续曲线,即A:[0,1]→S,B:[0,1]→S. 又设α和β是单位区间的2个重参数化函数,即α:[0,1]→S,β:[0,1]→S,则曲线A和B的Fréchet距离F(A,B)定义为 (1) 式中d是S上的度量函数. Fréchet距离是法国数学家Maurice René Fréchet在1906年提出的一种路径空间相似形描述,这种描述同时还考虑了路径空间距离的因素,对空间路径的相似性比较适用. 直观地理解,Fréchet距离就是狗绳距离,即主人走路径A,狗走路径B,各自走完这2条路径过程中所需要的最短狗绳长度,如图2所示. 图2 狗绳距离Fig.2 Distance of dog and rope 设P:[0,n]→V是一条曲线,用σ(P)表示曲线上所有的数据点,即σ(P)={u1,u2,…,up}. δdF(P,Q)=min {‖L‖} (2) 图3展示了离散化的Fréchet距离. 图3 离散Fréchet距离Fig.3 Discrete Fréchet distance 定义5轨迹夹角. 轨迹等价类中2条轨迹Ta={(x1,y1,t1,v1),(x2,y2,t2,v2),…,(xn,yn,tn,vn)}和Tb={(x1,y1,t1,v1),(x2,y2,t2,v2),…(xn,yn,tn,vn)}在时间段[ti,ti+1]内的移动向量为Ta[i,i+1]和Tb[i,i+1],那么时间段[ti,ti+1]内的轨迹夹角弦定义为 (3) 则轨迹Ta和Tb的夹角为 (4) 定义7轨迹距离. 设轨迹Tp={Idp,(x1,y1,t1,v1),…,(xn,yn,tn,vn)}和Tq={Idq,(x1,y2,t1,v1),…,(xn,yn,tn,vn)}的距离为 Distance(Tp,Tq)=F(Tp,Tq)=δdF(P,Q) (5) 本文提出一种基于Fréchet距离函数的轨迹隐私保护方法,该方法主要包含以下几个方面:1) 轨迹预处理,对轨迹进行预处理得到轨迹等价类;2) 计算轨迹等价类的Fréchet距离并将其存起来以供构建无向图时使用,对轨迹等价类中所有轨迹进行遍历,按照算法3构建轨迹图;3) 利用图划分算法对第2步形成的轨迹无向图进行划分,形成最终的轨迹k-匿名集合. 轨迹预处理过程有以下2个步骤: 1) 选取具有相同开始时间和结束时间的轨迹构造轨迹等价类;针对实际环境中的移动对象同时开始并且同时结束的数量非常少,为了减少信息损失率,本文选取一个给定时间间隔内的轨迹以确保轨迹间的高相似性. 2) 将第一步已经选取的轨迹通过轨迹同步化形成轨迹等价类. 算法1预处理算法(Pre-process) 输入:原始轨迹集合Tr. 输出:轨迹等价类T′r. (1)forTxinTr: (2) if 轨迹的开始、结束时间在给定范围内,那么 (3) 将Tx添加到T′r中 (4)for eachTi,Tj∈T′r (5) fortm∈Ot(Ti,Tj) (6) iftm∈tiandtm∉tj (7) 将tm时间点插入Tj中 (8) else 将tm时间点插入Ti中 (9)返回Tr 轨迹间的相似性通过轨迹的夹角和轨迹运动形状决定. 轨迹的形状越相似并且轨迹的夹角越小,轨迹的相似性越高;反之,轨迹的相似性越小. 尽管2条轨迹的夹角很小且形状相似,但2条轨迹的速度相差很大,目标轨迹也很容易被识别出来;因此,在构造轨迹图阶段有2个步骤: 1) 计算轨迹间的Fréchet距离,轨迹Fréchet距离通过算法2进行计算. 2) 构造轨迹图,利用轨迹间的夹角和轨迹的平均速度控制轨迹图的规模变化. 算法2Fréchet-轨迹距离算法 输入:轨迹的坐标位置P={(x1,y1),…,(xm,ym)},Q={(x1,y1),…,(xm,ym)}. 输出:δdF(P,Q). (1)初始化一个m×m的矩阵C,初始值均为-1 (2)functionC(i,j): (3) ifC(i,j)>-1,那么返回C(i,j) (4) else ifi=1 andj=1,那么直接计算(u1,v1)的距离 (5) else ifi>1 andj=1,那么递归计算C(i-1,1)的值并且C(i,j)为C(i-1,1)和(ui,v1)距离的最大值 (6) else ifi=1 andj>1 递归计算C(i-1,1),那么C(i,j)为(C(1,j-1),d(u1,vj))的最大值 (7) else ifi>1 andj>1,那么 (8) 递归计算C(i-1,j),C(i-1,j-1),C(i,j-1)的值并选择3个值中的最小值,然后计算d(ui,vi)的距离,返回最小值和的最大值 (9) elseC(i,j)=∞ (10) 返回C(m,m) 定义8轨迹图. 轨迹等价类Tr={T1,T2,…,Tn},Tr的轨迹图G=(V,E,W)是一个带权无向图,满足:V是轨迹图G的顶点集合,∀vi∈V都对应等价类中的一条轨迹Ti(1≤i≤n);E是轨迹图的边集,如果轨迹Ti和Tj满足(s,v)-约束,则顶点vi和vj之间存在一条边ei,j;W是一个n阶对称矩阵,∀wi,j∈W表示轨迹Ti和Tj的边权. 定义9轨迹图边权. 轨迹图G={V,E,W},任意轨迹Tp,Tq∈V,如果边(Tp,Tq)∈E,那么Tp和Tq的边权wp,q为 (6) 式中:β∈[0,1],α+β=1;Distance(Tp,Tq)是轨迹Tp和Tq的Fréchet距离;Min是等价类的最小距离;Max是轨迹间的最大距离. 本节给出了轨迹图的构造,其基本思想为:首先任取一条轨迹T1加入到集合V中,剩余轨迹加入集合V′中,任取V′中的一条轨迹T2与V中每一条轨迹判断它们是否满足(s,v)-约束,如果满足则计算2条轨迹的边权,并将T2放入集合V中,将边(T1,T2)放入边集E中,从集合V′中删除T2,重复此过程直到集合V′为空,具体算法描述如算法3所示. 根据移动轨迹的数据可用性和隐私保护程度的不同,本文提出一种使用方向特征α和距离特征β调整轨迹图边权的个性化方法,首先计算2个轨迹间的Fréchet距离和夹角,然后根据定义9计算轨迹图边权. 算法3构建轨迹无向图 输入:轨迹等价类Tr={T1,T2,…,Tn},轨迹夹角约束s,轨迹平均速度约束v,轨迹的距离特征β,轨迹方向特征α. 输出:轨迹图G. (2)Tr←Tr-T1 (3)当轨迹等价类Tr不为空时 (4)如果轨迹Ti在T中并且与V中所有轨迹Tj满足(s,v)-约束,那么 (5)计算轨迹距离Distacnce(Ti,Tj) (6)Wi,j←Weight(Ti,Tj)=αs+βDistance(Ti,Tj) (7)E←(Ti,Tj) (8)V←V+Ti (9) 从轨迹等价类Tr中删除Ti (10) 否则 (11)V←V+Ti (12)Tr←Tr-T 轨迹k-匿名集合受到轨迹隐私保护水平和数据可用性的影响. 每个用户要求至少k-1个相似用户,并且形成的匿名区域足够小,也就是要求轨迹的相似性s更大,轨迹间的距离F(a,b)足够小. 定义10合并代价.G1和G2是轨迹图G的子图,并且G1和G2交集为空,如果∃v∈G1,v′∈G2,边权为wv,v′,则合并代价为Min(wv,v′). 本文将构建轨迹k-匿名集合转化为图划分问题,其基本思想为:对于顶点数大于k的轨迹图,首先选择权重最小的边,将对应顶点加入集合V′中;其次,寻找与V′中相关联且权重最小的顶点加入V′中,重复此过程直到顶点小于k;对于顶点小于k的轨迹图,将其并入合并代价最小的匿名集合. 具体如算法4所示. 算法4轨迹匿名算法 输入:轨迹图G=(V,E,W). 输出:匿名集合T″r. (1)T″r=φ,V′=φ,w=φ (2)MinWeight=W0,1,r=0,s=1 (3)选择开始点,在轨迹图中寻找边权最小的顶点Vi,Vj,V′={Vi,Vj} (4)对V′中每个顶点v寻找所有与v关联的顶点,选择最小权值的顶点加入V′,重复此过程直到V′中的顶点数大于等于k (5)重复步骤4直到轨迹图所含顶点个数小于k (6)将顶点数小于k的集合并入合并代价最小的匿名集合 (7)返回匿名轨迹T″r={V′1,…,V′m} 本文所得到的匿名集合的基本思想为:首先,对原始数据进行轨迹预处理得到轨迹等价类;其次,将轨迹等价类转化为轨迹图;最后,通过轨迹图的划分得到相应的匿名集合. 轨迹的相关性依赖于权值数,即轨迹图的边权,轨迹的权值函数包含轨迹隐私和数据可用性. 本文从2个方面分析算法有效性,一是k-匿名的隐私保护程度,二是分析轨迹的信息损失率. 轨迹隐私保护主要通过攻击者从轨迹发布数据库中识别一个轨迹的概率来衡量. 本文构建的轨迹匿名集合通过轨迹图的划分构建,考虑到不同的隐私保护程度和数据可用性,提出了一个不同的构建轨迹k-匿名集合方法. 在计算轨迹距离时,采用一种考虑轨迹形状的Fréchet距离公式来计算,并且轨迹之间要求满足(s,v)-约束. 轨迹被重新识别的概率即为轨迹的隐私保护水平,是攻击者能够从轨迹发布数据库中区分轨迹信息点或者轨迹的概率. 本文通过分析轨迹间相关性来衡量轨迹的隐私保护水平,即分析轨迹间的相似性. 假设构造的k-匿名集合为T={T′1,T′2,…,T′k},并且每个轨迹满足定义1. 用轨迹匿名集合平均相似性Savg表示轨迹k-匿名集合的相似性,轨迹相似度Savg计算公式为 (7) 轨迹的隐私保护水平采用所有匿名集合的平均值表示,即 (8) 式中p表示形成的匿名集合个数. 在计算信息损失率时,仅仅考虑构建轨迹匿名集合时造成的信息损失,不考虑轨迹预处理的信息损失. 本文通过轨迹的匿名区域与整个轨迹空间区域面积的比值来衡量信息损失,轨迹匿名区域与数据可用性成反比,匿名区域面积越大数据可用性越小,反之数据可用性越大,表示为 (9) 式中:Area(xji,yji,tj)为tj时刻的匿名区域面积;MaxAreai为第i个匿名集合的最大面积;p为匿名集合的个数. 本文从2个方面分析算法的可行性和有效性,一是隐私保护水平,二是信息损失率. 把本文提出的基于Fréchet 距离函数的匿名算法和NWA[10]匿名算法以及将本文计算轨迹距离换成欧式距离进行对比实验. 本文的实验环境为Inter(R) Core(TM) i5- 4590 CPU @3.30 GHz;8 GB内存;Microsoft Windows 7.sp. 64位操作系统;本算法在pycharm中实现. 实验中使用的实验数据集是由Brinkhoff生成器基于德国奥尔登堡市交通地图生成的[16],初始数据集如表1所示. 第1列表示移动对象的编号;第2列是移动对象位置编号,即表示该点是轨迹的第几个位置;第3列表示数据返回的概率,0表示以百分百的概率生成数据点;第4列表示轨迹所处的时间;第5、6列表示轨迹所处的位置信息;第7列表示轨迹的当前速度;最后2列表示轨迹下一时刻将要到达的位置. 表1 部分数据 图4反映了在方向参数α=0.2和数据可用性参数β=0.8时,本文使用基于Fréchet 距离函数的轨迹匿名算法和基于欧氏距离的方法及NWA轨迹匿名算法的比较. 从图中可以看出,随着k值的增大轨迹的相似程度会逐渐变小,即隐私保护水平随之下降;基于Fréchet 距离函数的轨迹匿名算法要比NWA[10]轨迹匿名算法和基于欧氏距离的匿名算法所形成的轨迹匿名集合的相似度更高,即轨迹的隐私保护水平更高. 这是因为在构建匿名集合时不仅考虑轨迹的运动方向相近,同时它们的平均速度也必须相近,这就增加了构建的匿名集合之间的相似性,另外,Fréchet 距离函数在计算轨迹距离时考虑轨迹的形状使得轨迹间的相似性比其他方式构造的更高. 图4 不同方法的隐私保护水平Fig.4 Privacy protection level of different methods 在方向约束参数α=0.2和数据可用性参数β=0.8的约束下不同方法的信息损失比较如图5所示. 从图中可以看出,随着k值的逐渐增大,信息损失越来越大,但本文提出的算法信息损失略低于另外2种方法. 因为相比于NWA算法和采用欧氏距离度量轨迹距离的方法,本文基于Fréchet算法和(s,v)-约束将轨迹速度和运动方向、轨迹形状相似的轨迹匿名到一个集合,因此,产生的信息损失较小,数据利用率增大. 从实验中得出,本文提出的方法最大信息损失约为26%,而另2种方法最大信息损失约为34%,信息损失降低约为8%. 图5 不同方法对应的信息损失Fig.5 Information loss corresponding to different methods 图6显示了方向约束参数α和数据利用率参数β分别为(1.0,0)、(0.2,0.8)、(0.8,0.2)、(0,1.0)时本文提出算法的信息损失比较. 从图中可以看出,对于4种不同的(α,β)参数,轨迹匿名之后的数据信息损失并不完全相同,但是当β≠0时,不同k信息损失率相差并不大,这是因为本文算法所采用的距离计算函数在计算距离时考虑了轨迹的形状,增加了轨迹的相似性,所以相差不大. 当仅考虑轨迹的隐私保护时,轨迹间更为相似,但是轨迹间距离变得更大,导致匿名区域变大,因此,信息损失较大. 另外,从图中也可以看出,随着k增大,信息损失也越来越大. 图6 不同(α,β)的信息损失率Fig.6 Information loss rates of different (α,β) 图7为不同隐私保护参数α和数据利用率参数β分别在(0,1.0)、(0.4,0.6)、(0.7,0.3)、(1.0,0)四种情况下本文提出算法的运行时间比较. 从图7可以清晰地看出,在这4种情况下算法的运行时间基本相同,并且随着k值的增加而增加. 因为在这4种参数下,算法构造轨迹图的权重虽然不同,但是匿名集合的规模基本相同,故算法的运行时间大致相同. 另外,随着k值的增加匿名集合的规模变大,需要更多时间找到k条相似的轨迹,因此,算法的运行时间随着k值增加而增加. 图7 不同参数执行效率比较Fig.7 Execution efficiency of different parameters 图8为隐私保护参数和数据利用率取(0.3,0.7)时本文提出的算法和其他2种算法的执行效率比较. 从图中可以看出,几种方法的运行时间随着k值的增加而增加,这是由于随着k值增大,需要更多的时间寻找满足隐私需求的轨迹. 本文提出的算法综合考虑轨迹的夹角、距离、速度、形状等因素,同时设置了隐私保护参数,在构建匿名集合时约束条件更多,故运行时间相比其他算法稍长. 但在实际应用中,本文提出的方法能够提供较高的隐私保护和较好的数据利用,随着计算机硬件设备性能的不断增强,算法略高的开销是可以被接受的. 图8 不同方法的运行时间Fig.8 Different methods of run times 1) 基于Fréchet距离函数的轨迹隐私保护方法,在数据可用性和隐私保护程度方面都有所提高,虽然算法开销略高,但是,由于现在设备的性能高,算法开销仍可接受. 2) 利用图划分思想构建轨迹匿名集合,通过设定参数α和β的值能够更好地调节轨迹图的边权来实现隐私保护和数据可用性的动态平衡. 3) 提出的(s,v)-约束使得轨迹在运行方向相似,同时各个轨迹的速度也相近,从而使得攻击者更难识别轨迹,提高了轨迹隐私保护程度.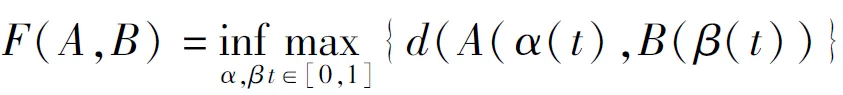

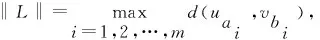
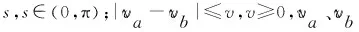
2 基于Fréchet 距离函数的轨迹匿名方法
2.1 轨迹预处理
2.2 构造轨迹无向图
2.3 构建匿名集合
3 轨迹隐私水平和数据可用性
3.1 隐私水平
3.2 信息损失率
4 实验结果分析
4.1 实验环境和数据
4.2 隐私保护水平
4.3 信息损失
4.4 算法运行效率分析
5 结论

