Improved prediction of slope stability using a hybrid stacking ensemble method based on finite element analysis and field data

Nvid Krdni, Annn Zhou,*, Mjidrez Nzem, Shui-Long Shen,b

a Civil and Infrastructure Discipline, School of Engineering, Royal Melbourne Institute of Technology (RMIT), Melbourne, Victoria, Australia

b Department of Civil and Environmental Engineering, College of Engineering, Shantou University, Shantou, 515063, China

Keywords: Slope stability Machine learning (ML)Stacking ensemble Variable importance Artificial bee colony (ABC)

ABSTRACT Slope failures lead to catastrophic consequences in numerous countries and thus the stability assessment for slopes is of high interest in geotechnical and geological engineering researches. A hybrid stacking ensemble approach is proposed in this study for enhancing the prediction of slope stability.In the hybrid stacking ensemble approach, we used an artificial bee colony (ABC) algorithm to find out the best combination of base classifiers(level 0)and determined a suitable meta-classifier(level 1)from a pool of 11 individual optimized machine learning (OML) algorithms. Finite element analysis (FEA) was conducted in order to form the synthetic database for the training stage (150 cases) of the proposed model while 107 real field slope cases were used for the testing stage. The results by the hybrid stacking ensemble approach were then compared with that obtained by the 11 individual OML methods using confusion matrix, F1-score, and area under the curve, i.e. AUC-score. The comparisons showed that a significant improvement in the prediction ability of slope stability has been achieved by the hybrid stacking ensemble (AUC = 90.4%), which is 7% higher than the best of the 11 individual OML methods(AUC = 82.9%). Then, a further comparison was undertaken between the hybrid stacking ensemble method and basic ensemble classifier on slope stability prediction. The results showed a prominent performance of the hybrid stacking ensemble method over the basic ensemble method. Finally, the importance of the variables for slope stability was studied using linear vector quantization(LVQ)method.© 2021 Institute of Rock and Soil Mechanics, Chinese Academy of Sciences. Production and hosting by Elsevier B.V. This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

1. Introduction

Slope stability refers to the condition of inclined soil slopes to withstand movement,which has significant effects on the safety of infrastructures,such as roads,dams,embankments,railways,open excavations, and landfills. A slope failure can be caused by several factors, acting together or alone, including rain water infiltration,snow melting,glaciers melting,rising of groundwater,physical and chemical weathering of soils,and ground shaking caused by either earthquakes or human activities. In reality, many slope failures were analyzed only after failure. The slope stability assessment is challenging because slope failure can be attributed to numerous factors as mentioned above as well as the difficulty to locate the most probable slip surface in the natural environments (Griffiths and Lane,1999; Griffiths and Fenton, 2004).

Slope stability analysis is one of the most traditional areas in geotechnical engineering. The stability of a slope is essentially controlled by the ratio of the available shear strength to the acting shear stress,which can be expressed in terms of a factor of safety(FOS)if these quantities are integrated over a potential(or actual)slip surface. Several key parameters play essential roles in slope stability, including slope geometry (i.e. height and slope angle),shear strength parameters (i.e. angle of internal friction and cohesion), pore water pressure, and soil properties (i.e. unit weight and degree of saturation) (Suman et al., 2016). The intricacy of the physical framework itself along with the complexity of determining the geotechnical parameters turns it into a very challenging task to estimate the stability of rock or soil slopes(Ghosh et al., 2013). Many endeavors have been made to develop new methods for estimating the stability of slopes, including analytical,numerical,and artificial intelligence based approaches(Qi and Tang, 2018a).

One of the earliest analytical methods based on the method of slicing to calculate slope stability is the limit equilibrium method(LEM) (Fellenius, 1936; Bishop, 1955; Bishop and Morgenstern,1960; Morgenstern,1965). Stability analysis of Chamshir dam pit in Iran, conducted by Faramarzi et al. (2017), is one of the examples which employ LEM to compute FOS.However,because of the simplifications and many assumptions which lead to the lack of thorough understanding of the behaviors of slopes, analytical methods(e.g.LEM)are just befitting to be used for slopes in small regions and with simple geometries(Song et al.,2012).Apart from the analytical method,numerical modeling is regarded as a more rigorous and realistic approach to assess slope stability (Li et al.,2016). Finite element method (FEM), one of the numerical methods based on displacement characteristics,has been used to calculate FOS (Baker, 2006; Huang and Jia, 2009). For example,Azarafza et al. (2017) numerically determined the discontinuous rock slope stability. Though numerical methods are computationally efficient, the need of back-analyzed input parameters which must be obtained from in situ measurement is a major drawback (Qi et al., 2017).

Machine learning (ML) techniques, which have been employed efficiently in geotechnical engineering in recent years(Atangana Njock et al., 2020; Elbaz et al., 2020; Shen et al., 2020;Zhang et al.,2020),provide an alternative way for assessing slope stability The relationships between the FOS and its influence variables are learnt from historical data(Cheng and Hoang,2013)using various ML algorithms. For example, Das et al. (2011) utilized differential evolution neural network to estimate FOS using the dataset from Sah et al.(1994).Artificial neural network(ANN)and particle swarm optimization (PSO) were employed by Gordan et al. (2016) to evaluate the seismic slope stability.Gandomi et al. (2017) carried out a study using evolutionary optimization techniques for slope stability analysis. Radial basis function neural network (RBFANN), extreme leaning machine,and least square support vector machine (LSSVM) were developed as a comparative study of slope stability evaluation by Hoang and Bui (2017). Qi and Tang (2018a) carried out a comparative study of slope stability prediction utilizing integrated metaheuristic and ML approaches, i.e. logistic regression(LR), decision tree (DT), random forest (RF), support vector machine (SVM), multilayer perceptron artificial neural network(MLPANN), and gradient boosting machine. They also used basic ensemble classifier consisting of 6 individual classifiers and majority voting as a combination method to improve analysis of slope stability (Qi and Tang, 2018b).

Various studies have been performed to evaluate the predictive performance of ML algorithms for slope stability. However,stacking ensemble ML methods and their significant roles in accelerating the predictive performance of ML algorithms have not been explored for estimate of slope stability. Stacking ensemble is a modern approach to create a model of a wellchosen collection of strong yet diverse models. Stacking ensemble is an efficient ensemble method in which the predictions, generated using various ML algorithms, are used as inputs in a second-layer learning algorithm. This second-layer algorithm is trained to optimally combine the model predictions to form a new set of predictions.Details on the ensemble systems will be presented in Section 2. In addition, a comprehensive comparative study of advanced soft computing methods is still lacking.

In this study,FEM was used to simulate the slope stability and generate synthetic data for the training of the optimized machine learning (OML) methods. This procedure has never been used in the literature, as the common procedure is to use data from the same source for both training and testing. By using this strategy,we can overcome the issues concerning the small dataset,i.e. the low accuracy of the model and over- and under-fitting problems.In addition,we can reduce the cost concerning the data collecting.It is important to note that,in order to preserve the consistency of the datasets and models,same input variables were used for both FE simulation and proposed model. The values of the input parameters in FE simulation were generated randomly to ensure that their means and standard deviations were close to the real data from the field.Afterwards,OML methods were employed to build the pool of classifiers. A hybrid stacking ensemble approach was then proposed in which an artificial bee colony (ABC) algorithm was utilized to find out the best combination of base classifiers and to determine a suitable meta-classifier from the pool of 11 OML algorithms.The proposed hybrid stacking ensemble method was then used to assess the slope stability on the testing dataset based on Sah et al. (1994), Li and Wang (2010), and Lu and Rosenbaum (2003), which consists of 107 samples from the real cases of the slopes(see Appendix A).Unit weight(γ),cohesion(c),angle of internal friction(φ),slope angle(β),slope height(H),and pore water pressure coefficient (ru) were employed as the input parameters of different ML models which will be explained with more details in Section 3.2.The capacity of the proposed ensemble method in assessing slope stability was compared with the 11 ML methods and that of the basic ensemble learning method by Qi and Tang (2018a). The advance of the proposed ML method for predicting slope stability was validated through different performance metrics, including confusion matrix, F1-score, and AUCscore.

2. Methodology

Ensemble systems, also known as a mixture of experts, are meta-algorithms that amalgamate multiple ML methods into one predictive model. The broad advantages of such a procedure in automated decision-making applications,specifically in the field of engineering, have lately been found by researchers and ML community. Ensemble learner performs better than individual learner.From the statistical point of view, it is an undeniable fact that appropriate performance of a classifier on the training dataset does not indicate a good performance on data which have not been seen during training (generalization performance). It means that, if the testing dataset is not a good representative of future field data,ML algorithms with the same generalization performances might have different predictive performances.This is precisely the reason that combining the outputs of different leaners may reduce the risk of an unfortunate prediction.

Stacking ensemble is one of the well-known ensemble methods in which two levels of classifiers,including base classifiers(level-0)and meta-classifier (level-1), are used to predict the output variable(s)(see Fig.1).Stacking ensemble combines the outputs of the base classifiers using the meta-classifier to learn the relation between model outputs and actual outputs.

One of the key points is to obtain the training data for level-1 model (Scv) by cross-validation (CV) technique. Given an original training dataset S = （yn， xn）（n = 1， 2， …，N）, ynrepresents the target value, and xnrepresents the feature vectors of the n-th instance which randomly split the data into K-fold S1, S2, …, SK(K = 10). Define SKand S（-K）= S-SKas the testing and training datasets for the K-th fold of K-fold CV,respectively.Given I different level-0 ML methods (C1, C2, …, CI), each Ciis trained by S（-K）and predict each instance x in SK.denotes the prediction of the model Cion x. Then, we have

where Pknrepresents the prediction on the training.

At the end of the entire CV process of each Ci,the data assembled from the outputs of the I model is

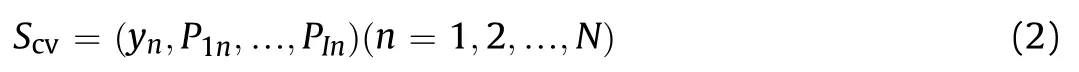
where Scvis the training dataset of level-1 model Cmeta.

To complete the training process,level-0 models Si(i=1,2,…,I)are trained using the original training dataset S,and Cmetais trained by Scv. Now we consider the prediction process, which uses the model Si(i = 1, 2, …, I) in conjunction with Cmeta. Given a new instance,model Siproduces a vector（P1，…，PI）.This vector is input to the level-1 model Cmeta, whose output is the final prediction result for that instance.

Two significant issues when using stacking ensemble are as follows:(1)in the level-0,how to select suitable classifiers to constitute the ensemble;and(2)in the level-1,how to select appropriate metaclassifier to aggregate the base classifiers. These two issues were described as “black art” by Wolpert (1992). To tackle these two issues, metaheuristic optimization algorithms have been applied by researchers to obtain the optimal configuration (Ledezma et al.,2002, 2010; Chen and Wong, 2011; Shunmugapriya and Kanmani,2013). In this study, we used an ABC algorithm to find out the best combination of base classifies and also to determine a suitable metaclassifier for the level-0 classifiers(see Fig.2).

2.1. Pool of classifiers

In this study,11 individual ML methods were used to form the pool of classifiers. These methods were selected as they have already been applied to the slope stability dataset.For the training of the ML algorithms,FEM was used to generate 150 cases of stable and unstable slopes.For validation of the algorithms,107 real cases of slopes were studied. The proposed hybrid stacking ensemble method uses ABC algorithm to select the best combination of baseclassifiers as well as meta-classifier from the pool of classifiers.Hybrid stacking ensemble and ABC algorithm will be explained later in this section.A brief introduction to these methods and their applications in the slope stability analysis is as follows:

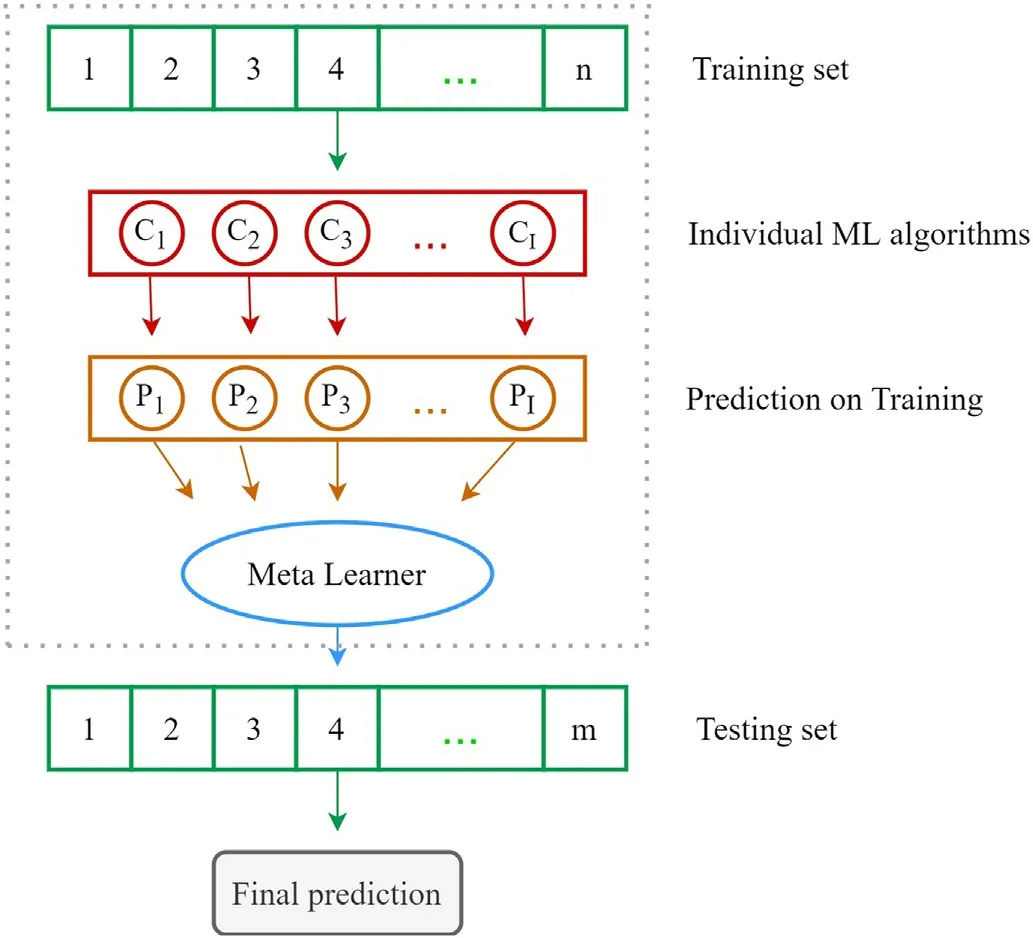
Fig.1. Illustration of stacking ensemble.

(1) Support vector classifier (SVC)

As a supervised learning method, SVM is commonly used for three main purposes including classification (SVC), pattern recognition, and regression (SVR) problems. Fast calculation process to attain global optimum and robust performance to overcome the overfitting problem are some considerable features which make SVM a better method in comparison with the simple ANN (Wang,2005; Baghban et al., 2017). The SVC has been used to predict the stability of slopes by many researchers (e.g. Cheng et al., 2012; Li et al., 2013; 2015; Hoang and Pham, 2016; Kang et al., 2016). They found that SVC models have more advantages to slope stability evaluation over ANN models under the condition of limited data.

(2) K-nearest neighbor (KNN)

KNN algorithm is a non-parametric supervised classification method in which a case is classified by assigning weight to the contributions of the neighbors(Altman,1992;Garcia et al.,2012).In other words, KNN algorithm is based on feature similarity and the structure of the model is determined from the data. The KNN algorithm has been used for slope stability analysis.For example,Bui et al. (2017) built an instance-based classifier relied on the fuzzy KNN slope stability assessment. Furthermore, Cheng and Hoang(2014) established a method integrating the Bayesian framework and the KNN technique to achieve probabilistic slope stability analysis,where the KNN algorithm is employed to approximate the conditional probability density functions.

(3) Decision tree(DT)

DT is a classification method in which models are built in a flowchart-like structure. DT consists of decision nodes and leaf nodes.The dataset should be broken down into smaller subsets while an associated DT is incrementally developed. The DT algorithm has been adopted for slope failure prediction.For example,Glastonbury and Fell(2008)presented DTalgorithms and supporting matrices to allow assessment of the likely post-failure velocity of translational and internally sheared compound natural rock slope landslides.General slope factors were analyzed and classified using a DT algorithm to evaluate the validity of the Korean slope database that consists of 6828 slope observations(Hwang et al.,2009).Nefeslioglu et al.(2010)assessed landslide susceptibility bya DTalgorithm in the Metropolitan Area of Istanbul,Turkey.Hong et al.(2018)employed a DTalgorithmwith Ada Boost,Bagging and Rotation Forest to analyze landslide susceptibility in Guangchang area.

(4) Extreme gradient boosting (XGB)

Gradient boosting machine (GBM) is another ML method which makes a prediction model utilizing weak prediction techniques,such as DT. XGB which belongs to the family of boosting algorithms is a method that has been utilized in applied ML in recent years.It is also an implementation of gradient-boosted DT designed for speed and performance and refers to the engineering goal to push the limit of computationresourcesforboostedtreealgorithms.Gradientboosting has also been employed in geotechnical analysis recently. For example, Ding et al. (2018) predicted the pillar stability for underground mines by using the stochastic gradient boosting technique.

(5) Random forest(RF)

Fig. 2. Comparison between previous studies and current study.

As an ML technique (based on the divide-and-conquer approach), RF is comprised of DTs using bagging methods(averaging the prediction over a collection of classifiers). In order to correct DTs’ habit of overfitting to their training dataset,random forests create DTs based on randomly selected data samples, obtain a prediction from each tree, and select the best solution by means of voting. Moreover, it provides a fairly good indicator of the feature importance (Ho, 1995). The RF has been used to predict slope stability (Wen and Zhang, 2014; Lin et al.,2018; Qi et al., 2018) and landslide susceptibility (Youssef et al.,2016).

(6) Linear discriminant analysis (LDA)

As a type of linear combination, LDA comprises of statistical properties of the data,uses mathematical process with various data items, and applies functions to the dataset to analyze multiple classes of items. Supposing a Gaussian distribution and multiple variables,LDA considers the mean value of each class as well as the covariance matrix to make predictions. LDA has been used to predict susceptibility of landslide (Dong et al., 2009; Ramos-Cañón et al., 2016) and slope stability (Liu and Chen, 2007; Gao and Yan,2010; Ke, 2010; Dong and Li, 2013).

(7) Multilayer perceptron artificial neural network (MLPANN)

ANN is a data-driven method inspired by the structure of a brain. ANN uses different layers of mathematical processing to learn from observing dataset. Multilayer perceptron (MLP) is a classical type of ANN. It is comprised of an input layer, an output layer and one or more hidden layers between input and output layers (Kardani and Baghban, 2017; Kardani et al., 2018; Ghanbari et al., 2020). The hierarchical or multi-layered structure of the MLP makes it capable of learning nonlinear functions. In MLP,backpropagation algorithm compares the expected output and the output of the network to calculate the error.ANN was used for slope stability prediction by Sakellariou and Ferentinou(2005).

(8) Logistic regression (LR)

LR predicts the probability of a binary outcome. LR is used to describe data and to explain the relationship between one dependent binary variable and one or more nominal, ordinal, interval or ratio-level independent variables. Mathematically, a binary logistic model has a dependent variable with two possible values, which is represented by an indicator variable, where the two values are labeled “0” and “1”. LR has been used to analyze slope stability by Sari (2019) and found successful in landslide susceptibility assessment(Ohlmacher and Davis,2003;Ayalew and Yamagishi, 2005; Yilmaz, 2009; Ramos-Cañón et al., 2016;Tsangaratos and Ilia,2016;Aditian et al.,2018;Kalantar et al.,2018).

(9) Extremely randomized tree(ETs)

ETs is a recently proposed unpruned tree-based method for supervised classification. ETs selects attributes and cut-points in a random-wise procedure while splitting a tree node. ETs algorithm has two important parameters, including krwhich determines the strength of the randomization of the attribute, and nminwhich controls the degree of smoothing. From a functional point of view,the ETs method produces piece-wise multilinear approximations,rather than the piece-wise constant ones of RF(Geurts et al.,2006).

(10) Naïve Bayes (NB)

NB is a simple but surprisingly powerful algorithm for both binary and multiple class classification problems. Since NB uses strong independence assumptions between the features based on Bayes’theorem, it can be categorized as a probabilistic classifier (Tsangaratos and Ilia, 2016). Gaussian NB (GNB) is one of the extended versions of NBwhich issimple and the mostpopular one.GNB has been usedin different slope stability analyses(Feng et al.,2018;Lin et al.,2018)and landslide susceptibilities(Chen et al.,2017;He et al.,2019).

(11) Bagging classifier (BC)

Bootstrap aggregation, also known as BC, is a learner that trains each base classifier on random redistribution of the original training dataset. Then, each prediction of the classifiers is aggregated using averaging or voting methods to receive a final prediction (Breiman,1996). BC, which is a meta-estimator, can be used to improve the accuracy of ML algorithms as well as reduce the variance which can facilitate avoiding overfitting.BC has been used as a prediction tool for landslide susceptibility(Pham et al.,2017;Chen et al.,2018).

2.2. Artificial bee colony (ABC) optimization

As a relatively new and popular swarm intelligence based algorithm,ABC algorithm is inspired by the foraging behavior of the honey bee. ABC was introduced by Karaboga and Basturk (2007,2008) and is served as an optimization tool in a wide domain.Kumar and Prakash(2014)used ABC algorithm to perform a multitarget tracking for mobile sensor network and the results were found to be quite efficient.Babu et al.(2011)used ABC optimization along with ML algorithms to create sheep and goat disease database. Wijayanto and Purwarianti, (2014) employed ABC algorithm and fuzzy logic to improve the limitation of fuzzy geo-demographic clustering algorithm. The proposed method gives better clustering quality than the fuzzy geographically weighted clustering (FGWC)algorithm. Zhang and Wu (2011) introduced a method for image processing using the ABC algorithm. ABC algorithm and its development and applications were reviewed by Datey et al. (2017).

ABC is constituted of employed bee,onlooker bee,scout bee,and food sources which represent the possible solutions of the problem.The fitness of the solutions corresponds to the nectar amount of food sources. The steps of the ABC optimization are as follows:

(1) Generate an initial random population of solutions (xi）,i∈｛1，2，…，npop｝, where npopis the number of food sources;

(2) Assign each employed bee to a food source, and the population of employed bees equals npop;

(3) Employed bees exploit the population;

(4) Employed bees evaluate the solution;

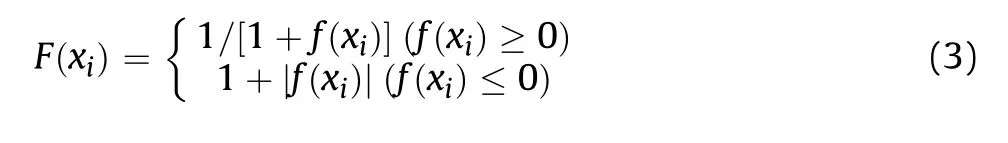
where F（xi） is the fitness value, and f（xi） is the objective function.

(5) Onlooker bees start to search the solutions(xk)based on the probability values(Pi)associated with solutions(xi),and the population of onlooker bees equals npop:

Onlooker bees compute the new solutions (Vi) using the following equation:

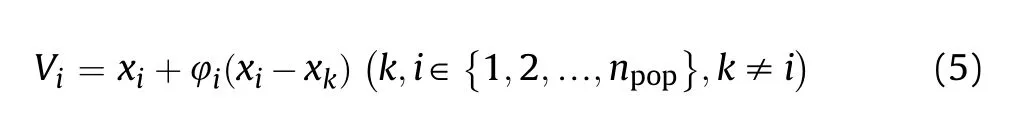
where Viis a new solution, xiis the current solution,φiis a random number(φi～u（ -1，1）)to control the production of neighbor food sources around xi, and xkis an onlooker solution.

(6) If Viis larger than xi,then Vibecomes xi;otherwise xiremains as such.

(7) If a position could not be further improved through a predetermined number of cycles(limit),then that food source is assumed to be abandoned, and scout bees replace the food source of which the nectar is abandoned by the bees with the randomly generated position, see Eq. (6).

where xiis the abandoned source,are the lower and upper bounds of parameter j(j∈｛1，2，…，D｝),and D is the dimension of the problem.

It is important to note that the ABC is controlled by three parameters,including the value of limit,the maximum cycle number (MCN), and the number of food sources npop.

2.3. Hybrid stacking ensemble

In this method,the classifier configuration of stacking ensemble is optimized by the ABC algorithm. It is worth mentioning that before implementing the proposed model,11 individual ML models which build the pool of classifiers were calibrated using PSO algorithm. During the implementation of the model, ABC algorithm plays a role as a selection tool to find out the optimized (best)combination of the classifiers for the stacking ensemble. This process results in a hybrid stacking ensemble model which is optimized in two ways: (1) the configuration of ensemble, and (2)hyperparameters of the base- and meta-classifiers. The pseudo code of hybrid stacking ensemble is presented in Appendix B.

The bees exploitand explore a setof classifiers C,where C = ｛1，2，…，Sn｝,in order to attain a subset S,where S = ｛1，2，…n｝and n ≤Sn,to obtain a maximum possible prediction accuracy. Each employer bee is assigned a classifier.First,10-fold CV is executed to calculate the prediction accuracies(xi）of the classifiers.Since the method aims to maximize(xi)using an optimal combination of classifiers,the objective function(f（xi）)is assigned by the prediction accuracy.Then,Eq.(3)isusedbyanemployed bee to evaluate fitnessF（xi）of theclassifier.The onlooker bee of each classifier executes neighborhood search and selects a classifier based on the Eq. (4). Next, a new solution is calculated by onlooker bee using Eq.(5)based on the accuracies of the classifier.The onlooker bee is currently selected by xk,with which the employed bee is already assignedxi. Greedy selection is applied by onlooker bee to include selected classifier in the best configuration.According to step 7 in ABC algorithm,if Viis larger than xi,then the selected classifier is added to the best classifier subset(Si)by onlooker bee;otherwise,Siremains as such.At this stage,bees search for the best meta-classifier in C to maximize the prediction accuracy of that configuration.Theemployedbeeisassignedbythe stackingensemble and the prediction accuracy of the stacking ensemble will be the new xi.Based on aforementioned discussion,after the completion of the bee exploitation cycle,better classifier configurations can accumulate more nectar.If the solution from an employed bee does not improve through a predetermined number of cycles(limit),then the employed beeofthatclassifierbecomesascoutandisassignedtoanewclassifier source. The new classifier position is computed using Eq. (6). The exploration of the bees to generate subset configurations of classifiers continues till a better configuration is found (Shunmugapriya and Kanmani, 2013). Hybrid stacking ensemble uses the ABC algorithm to find out the best(optimized)combination of the base-and metaclassifiers from a pool of 11 individual ML algorithms, in order to improve the estimation of the individual ML algorithms.It should be noted that ABC algorithm does not do any classification task to identify the stable and unstable slopes.ABC optimization is working as a selection method to obtain the best configuration of the stacking model.

As it can be seen from Fig. 2, in comparison to the previous studies,i.e.individual ML approaches and basic ensemble classifier(Qi and Tang,2018b),a hybrid stacking ensemble learner applied to the dataset of slopes has two prominent advantages as follows:

(1) In the level-0, despite basic ensemble methods which have no specific rule, determination of the set of base-classifiers among different configurations of ML algorithms is done by the ABC optimization algorithm.This can lead the model to a better classification.

(2) In the level-1,the prediction,generated by the ML algorithms in the level-0,is used as an input for a meta-classifier which is selected by the ABC algorithm in a simultaneous procedure. This meta-classifier is trained to optimally combine the predictions of models from a new set of predictions.While in the basic ensemble, there is no such an approach.

Parameter of hybrid stackingensemble consists of population size,limit(i.e.themaximumnumberofiterations),φ(i.e.randomnumber),and the number of runs. The bee colony has the same number of onlooker bees and employed bees are equal to the number of food sources. In this study,11 classifiers form the pool of the classifiers.Hence, the bee population has 11 employed bees and 11 onlooker bees.Table 1 shows the parameters of the hybrid stacking and their values.

Finally,a combination of four ML methods which are strong and with adequately different decision boundaries from LR, GNB, MLP,and BC as base-classifiers,and LR as a meta-classifier,has achieved the best accuracy.It is interesting that BC which itself is an ensemble meta-estimator was used as one of the base-classifiers of the stacking ensemble learner.It is also important to note that,based on no-free-lunch theorem, it is not possible to find out an algorithm with the best performance for all classification problems.Hence,the best classifier depends on the dataset and prior knowledge.

Table 1 Hybrid stacking parameters.

3. Measures and data

3.1. Performance metrics

In this study, confusion matrix, F1-score and AUC-score were used to measure the accuracy of the hybrid stacking ensemble and OML methods as well as to compare them to find out the best classifier for the slope stability.

3.1.1. Confusion matrix

Confusion matrix(see Table 2),also known as error matrix,is a tabular summary used to describe and visualize the performance of a supervised ML algorithm such as classification.

According to Table 2,some metric values,i.e.accuracy（ACC =（TP + TN）/（TP + TN + FP + FN））, recall （TPR = TP/（TP + FN））,true negative rate （TNR = （TN/TN + FP））, precision （PPV =TP/（TP + FP））, and false positive rate （FPR = FP/（FP + TN））, can be defined.

3.1.2. F1-score

F1-score, also known as F-measure, can be used as a metric to measure the accuracy using both precision(PPV)and recall(TPR)of the test. In other words, F1-score reaches its best value at 1 and worst at 0 through the harmonic average of the precision and recall as expressed by

When it comes to uneven class distribution,F1-score might be a better measure to use.

Table 2 Confusion matrix.

3.1.3. AUC-score

The receiver operating characteristic(ROC)curve plots TPR against FPR at various cutoff values.This graphical plot can be used to express the prediction ability of a classifier.The AUC or the area under the ROC curve is commonly used as a measure of the accuracy of classification.The AUC value ranges from 0.5 to 1 indicating the best and worst accuracy, respectively. Hosmer et al. (2013) proposed a guide for classifying the AUC-score values as follows: outstanding(0.9 < AUC < 1), excellent (0.8 < AUC < 0.9), and acceptable(0.7

Fig. 3. Input features for an earth slope stability analysis.

3.2. Data preparation

In this section, input attributes are introduced and the data preparation procedure including data collecting for training and testing datasets and CV method is explained herein.

3.2.1. Input features selection

In order to assess the stability of the slope, it is necessary to select the most influence factors.For this purpose,six features,i.e.unit weight (γ), cohesion (c), angle of internal friction (φ), slope angle(β),slope height(H),and pore water pressure coefficient(ru),were selected as input attributes according to the literature (see Fig.3).The output of the model is the status of the slope which can be either stable or unstable. In this study, slopes with FOS larger than 1.3 were considered stable.

3.2.2. Data collection

In this paper, FEM was used to simulate the slope stability and generate data for the training of the ML methods. Afterwards, ML methods which had already been trained were employed to predict the slope stability on the testing dataset which consisted of the real cases of the slopes.

(1) Training dataset

To construct the training dataset,150 slopes were studied using the finite element(FE)module in OptumG2 simulation software 2019(Krabbenhoft et al., 2015), with Mohr-Coulomb (MC) considered as the material model. Since the slope stability is predicted, we more care about the strength of the soil other than the deformation. The MC criterion is used as the strength envelope. Within the strength envelope,the material is assumed as elastic,which is widely used for slope stability analysis. The elasticity parameters are used: Young’s modulus of 100 kPa and Poisson’s ratio of 0.3.Six input variables are randomly determined with seed(10),in a way that their means and standard deviations are close to the real data from the field (see Table A1 in Appendix A).Fig.4 shows an example of FE simulation of the slope stability with mesh adaptivity, 2000 elements,γ=14.59 kN/m3,c=10.92 kPa,φ=27.55°,β=47.11°,H=141.66 m and ru= 0.1, the upper and lower parts of Fig.4 show the slopes at first and last iterations, while Table 3 shows the summary of data samples in the training dataset through their statistical values.

(2) Testing dataset

In the present study,the trained ML methods were applied to a testing dataset which consisted of 107 samples of slopes collected from the literature (Sah et al.,1994; Lu and Rosenbaum, 2003; Li and Wang, 2010) (see Table A2 in Appendix A). Table 4 presents the summary of data samples in the testing dataset through their statistical values, while Figs. 5 and 6 are the correlation pair panel and heat map of a correlation matrix,respectively,which illustrate the correlation between parameters.

Fig.4. FE simulation of slope stability:(a)mesh adaptivity,and(b)distribution of the internal shear dissipation associated with the Mohr-Coulomb soil constitutive model,colors represent the intensity of dissipation along the slip surface (the blue color denotes low intensity whereas the red color represents a relatively high intensity).

Table 3 Summary of the training dataset (count = 150).

Table 4 Summary of the testing dataset (count = 107).

Fig. 5. Correlation pair plots of input variables for testing dataset.

Fig.6. Heat map of correlation matrix of six input and one output variables for testing dataset.

Fig. 7. Procedure of the K-fold CV.

Fig. 8. Average AUC scores along with iterations on the training dataset.

3.2.3. K-fold CV

CV is a method used to evaluate the prediction ability of a model on an independent dataset. There is always a risk of overfitting or selection bias (Cawley and Talbot, 2010) for prediction models. To address these problems, CV method can be applied to the dataset.In this study,the 10-fold CV,which is the most commonly used CV method, was applied to the training dataset (see Fig. 7). The validation phase is used to examine the robustness of trained ML models before evaluating model performance via the testing dataset. However, existing ML-based soil constitutive models did not include the validation phase. The K-fold CV procedure can be conducted as follows:

(1) Shuffle the dataset randomly and partition it into K equal sized group/fold;

(2) Take one-fold as a validation dataset and the remaining ones as a training dataset;

(3) Fit the model on training and test it on a validation dataset,respectively; and

(4) Repeat these steps for all K-folds and retain the evaluation scores.

Table 5 Optimum values of hyperparameters.

4. Results, comparisons and discussions

As mentioned previously,in the first step of the current study,a hybrid stacking ensemble model was applied to the dataset of 257 samples in order to analyze the slope stability.The results were then compared with 11 OML methods on the variety in the nature of algorithms and performances.Furthermore,a comparative study was conducted to indicate the superiority of the hybrid stacking ensemble over the basic ensemble classifier.Finally,to evaluate the importance of variables, LVQ algorithm (Pourghasemi and Rahmati, 2018) was applied.

4.1. Results of hyperparameter tuning

Modern supervised ML algorithms involve hyperparameters that have to be set before running them.The performance of an ML algorithm can be highly dependent on the hyperparameters.For example,in RF,min_samples_split is a parameter that tells the DT in a RF,the minimumrequired numberofobservationsinanygiven nodeinorder to split it;while min_samples_leaf specifies the minimum number of samples that should be presented in the leaf node after splitting a node.Hyperparameters and their application to ML algorithms were fully discussed by Probst et al.(2018).There are several methods for hyperparameter tuning of ML algorithms, e.g. evolutionary optimization,Bayesian optimization,gradient-based optimization,population based training,grid search,and random search.In this study,PSO algorithmwasusedtotune thehyperparameters(Kardanietal.,2020)(see Appendix b for complete explanation of the hyperparameter tuning process). Fig. 8 shows the change of AUC-score along with iterations of individual ML algorithms on the training dataset. Also,Table 5 shows the hyperparameters of ML methods and the optimum value for each ML algorithm.

Fig. 9. TPR and TNR of the hybrid stacking ensemble and individual methods.

4.2. Comparison between hybrid stacking ensemble and individual classifiers

In this section, the performance metrics mentioned in Section 3.1 were used to evaluate and compare the predictive performance of the 11 ML methods and the proposed ensemble machine.

Table 6 shows the testing dataset confusion matrix of the ML algorithms and stacking ensemble. As shown in Table 6, the highest accuracy between the individual methods belongs to the SVC and LR(ACC = 0.82). However, MLP showed excellent performance(ACC = 0.81) and XGB, LDA, ETs, GNB, and RF exposed acceptable performances (ACC > 0.7). According to confusion matrix, KNN(ACC = 0.69), DT(ACC = 0.67), and BC (ACC= 0.66) had the lowest accuracy among these models.Hybrid stacking ensemble shows the best performance in predicting slope stability (ACC = 0.91). It is notable that the prediction accuracy was successfully accelerated by about 9%using the stacking ensemble machine,which is a significant improvement.

The TPR and TNR are shown in Fig. 9. As illustrated, the most successful individual ML methods in the TPR are the SVC,MLP and LR(TPR > 0.8). Hybrid stacking ensemble also predicted 55 out of 60 unstable slopes as unstable (TPR = 0.9). However, in the TNR, the highest TNR achieved by the LR was 0.84,whilst the hybrid stacking ensemble achieved the TNR of 0.932.It is interesting to mention that in most cases,the TPR achieved by the individual ML algorithms and hybrid stacking ensemble is in the same range as TNR.This means that abilities of ML algorithms and the proposed hybrid stacking ensemble to predict slopes as stable or unstable are almost equal.

According to F1-score of testing dataset (see Table 7), high variation in model’s accuracy can be seen among the individual learners.The LR(F1-score=0.795)has the highest model accuracy among ML methods, followed by the SVC (F1-score = 0.791), MLP(F1-score = 0.77), XGB (F1-score = 0.764), LDA (F1-score = 0.762),GNB (F1-score = 0.723), ETs (F1-score = 0.711), RF (F1-score = 0.634), BC (F1-score = 0.581), KNN (F1-score = 0.571), and DT (F1-score = 0.567); while F1-score of hybrid stacking ensemble learner is 0.905 which indicates 11%progress in comparison to the best ML algorithm, i.e. LR with F1-score of 0.795.

Table 7 also shows the AUC-score of the 11 ML methods and proposed ensemble method.It can be seen that the testing dataset AUC values for MLP, LR, SVC, and LDA are 0.829, 0.827, 0.815, and 0.801, respectively, which could be considered as excellent classifiers (AUC > 0.8). They are followed by RF (AUC = 0.791), KNN(AUC = 0.784), XGB (AUC = 0.77), ETs (AUC = 0.741), GNB(AUC = 0.734) and DT (AUC = 0.727). BC has the lowest accuracy(AUC = 0.712) among individual classifiers. By contrast, hybrid stacking ensemble machine accelerates the performance of evaluating slope stability up to AUC=0.904,which shows its outstanding efficiency and a significant improvement of the performance(approximately 7%) compared with that of MLP (AUC = 0.829).

Fig.10 shows the huge variance of the performances of 11 OML algorithms and hybrid stacking ensemble on the testing dataset.According to Fig.10,the hybrid stacking ensemble outperforms the 11 OML algorithms. The curve related to the hybrid stacking ensemble is closer to the top and left axes than others, denoting that a higher overall performance is achieved by this model.

Table 7 Performances of ML algorithms.

4.3. Comparison between hybrid stacking ensemble and basic ensemble classifier

In this section, the performance of the hybrid stacking ensemble was studied through a comparative study between optimized stacking ensemble machine and basic ensemble machine proposed by Qi and Tang, (2018b) Basic ensemble classifier combines several classifiers to improve the generalization ability of individual methods using voting technique. However, voting technique is not efficient when selecting the optimized combination by which the decision-making quality of the ensemble is superior to that of any single model. Determining the optimized combination for various classifiers is one of keys to enhance the capacity of ensemble, which can be achieved by the hybrid stacking ensemble. In order to compare the prediction ability of the hybrid stacking ensemble and a basic ensemble classifier,three aforementioned metrics were used. Therefore, the 11 ML methods were used to build an ensemble and the results were then amalgamated using majority voting method.

Fig.10. ROC curves of OML algorithms and hybrid stacking ensemble.

Table 8 Confusion matrix of ensemble algorithms.

Table 9 Performance of ensemble algorithms.

As shown in Table 8, according to the confusion matrix, the accuracies of the hybrid stacking ensemble and basic ensemble classifier are 0.91 and 0.794, respectively, which indicates the dominant performance of hybrid stacking ensemble. According to Table 9, F1-score and AUC-score of the hybrid stacking ensemble method are 90.5%and 90.4%,respectively,which are approximately 14% and 11% higher than that of the basic ensemble (F1-score = 76.6%, AUC = 79.1%). It is interesting to note that the basic ensemble shows a lower performance than some individual classifiers,i.e.MLP(ACC=0.83),LR(ACC=0.83),SVC(ACC=0.81),and LDA(ACC=0.8).This means using the basic ensemble method does not show any improvement for this dataset.

Fig. 11 shows the variance of the performances of basic ensemble and hybrid stacking ensemble on the testing dataset. As depicted in Fig. 11, the performance of the hybrid stacking ensemble is much better than that of the basic ensemble classifier.It means that, hybrid stacking ensemble which uses an optimized algorithm to set the classifiers at level-0 and level-1 of the ensemble is more efficient than a basic ensemble classifier.

It should be mentioned that one of the most important advantages of the ML methods is their fast computation.Comparing these methods to the numerical methods,e.g.FEM,the computation time is quite short.For example,in this study,first 150 cases are used to train the model.Once the model is trained,it is ready to be used as a prediction tool to identify the stability of a slope case, which suggests that the model can be regularly trained once in a period of time to obtain new results to improve the prediction accuracy. At this stage,the computation time for the method can be obtained by running the trained model for a single testing case, which is approximately 1.5 s in this study. In order to obtain the computation time for the same slope case using FEM, OptumG2 software 2019 was used and the computation time was determined to be approximately 15 s.It is worth mentioning that all the 107 cases in testing dataset can be modeled at once using a trained ML method,but in case of FE modeling, same procedure should be performed 107 times to receive the same result. This shows the substantial superiority of the proposed model in reducing the computation time.However,there are the most marked limitations of this study:(1) using ensemble methods reduces the model interpretation ability due to increased complexity,and(2)ensemble models, like other AI based tools,greatly depend on the quality and quantity of the data for the training stage of the modeling.

Fig.11. ROC curves of hybrid stacking ensemble and basic ensemble classifier.

Fig.12. Importance of input variables.

4.4. Variable importance analysis for slope stability

In this section, further study was conducted to investigate the role of each influence variable, i.e. input variables of the hybrid stacking ensemble method, in slope stability analysis. For this purpose, linear vector quantization algorithm is applied to the dataset of slope cases in order to indicate the influence variables for slope stability analysis. Fig. 12 shows the results of variable importance analysis for the dataset of this study. The slope height and cohesion are two most important variables with the importance values of 28% and 15%, respectively, followed by unit weight (12%), slope angle (11%), friction angle (10%), and porewater pressure coefficient (approximately 3%).

5. Conclusions

In this study, a hybrid stacking ensemble method was constructed upon 11 OML algorithms using ABC optimization technique to classify the slope cases into two classes: stable and unstable. FEA was used to build the training dataset for the proposed model and the 10-fold CV was used as the validation technique. PSO algorithm was conducted to optimize the hyperparameters of the ML methods including LR,RF,ETs,DT,XGB,GNB,SVC,LDA,MLP,KNN,and BC.Confusion matrix,F1-score,and AUC-score were used as performance metrics to evaluate the accuracy of the models. The proposed hybrid stacking ensemble which had already been trained by the synthetic data was applied to 107 real field cases of the slopes to accelerate the performance of ML algorithms. The variable importance was studied using LVQ algorithm to evaluate the influence of the input variables.

Simulation results of synthetic and experimental data indicated that MLP has the best predictive performance among the other algorithms (AUC = 82.9%), followed by LR (AUC = 82.7%), SVC(AUC=81.5%),and LDA(AUC=80.1%).It is interesting to note that all these ML algorithms showed an excellent predictive performance (AUC > 80%) (Hosmer et al., 2013).

Comparisons between the 11 OML algorithms and the hybrid stacking ensemble classifier indicate that the ensemble model achieved a better AUC-score than OML algorithms did. The AUC value for the stacking ensemble was 90.4% which illustrates that using hybrid stacking ensemble can accelerate the performance for the slope stability prediction. Comparison between the proposed hybrid stacking ensemble method and basic ensemble classifier shows the superiority of the hybrid stacking ensemble learner.Variable importance shows that slope height and cohesion are the most influence variables to assess the stability of the slope for this dataset, achieving importance scores of 28% and 18%,respectively.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work presented in this paper.

Acknowledgments

We acknowledge the funding support from Australia Research Council (Grant Nos.DP200100549 and IH180100010).

Appendix A. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.jrmge.2020.05.011.