Predicting uniaxial compressive strength of serpentinites through physical, dynamic and mechanical properties using neural networks

Vassilios C. Moussas, Konstantinos Diamantis

Department of Civil Engineering, School of Engineering, University of West Attica, Campus 1, Ag. Spiridona Str., Egaleo, Athens,12243, Greece

Keywords: Rock mechanic Serpentinites Uniaxial compressive strength (UCS)Artificial neural networks (ANNs)Physical, dynamic and mechanical properties

ABSTRACT The uniaxial compressive strength(UCS)of intact rock is one of the most important parameters required and determined for rock mechanics studies in engineering projects. The limitations and difficulty of conducting tests on rocks,specifically on thinly bedded,highly fractured,highly porous and weak rocks,as well as the fact that these tests are destructive, expensive and time-consuming, lead to development of soft computing-based techniques. Application of artificial neural networks (ANNs) for predicting UCS has become an attractive alternative for geotechnical engineering scientists. In this study, an ANN was designed with the aim of indirectly predicting UCS through the serpentinization percentage, and physical, dynamic and mechanical characteristics of serpentinites. For this purpose, data obtained in earlier experimental work from central Greece were used. The ANN-based results were compared with the experimental ones and those obtained from previous analysis.The proposed ANN-based formula was found to be very efficient in predicting UCS values and the samples could be classified with simple physical, dynamic and mechanical tests, thus the expensive, difficult, time-consuming and destructive mechanical tests could be avoided.

1. Introduction

Uniaxial compressive strength (UCS) of intact rock is a key,pertinent and important characteristic required in rock mass classification. This property is widely used in the design stage of geological and geotechnical engineering applications, such as tunnel and dam design, rock blasting, slope stability, foundation engineering, and underground excavation. The UCS of intact rock is determined experimentally through either direct or indirect methods.The direct determination of UCS is achieved by testing the specimens in the laboratory in accordance with the International Society for Rock Mechanics and Rock Engineering (ISRM) and American Society for Testing and Materials (ASTM) specifications.This way is complicated because it requires high-quality core samples of proper geometry. However, preparing high-quality cores, particularly from weak, highly fractured, thinly bedded,foliated and/or weathered rocks,is a difficult task.In addition,this test is destructive, time-consuming and expensive. To overcome these limitations and difficulties associated with the experimental procedure,the indirect prediction of UCS using rock index tests is of interest. Thus, empirical correlations among various physical, dynamic and mechanical properties of rocks to estimate the UCS have been developed by many researchers(e.g.Fahy and Guccione,1979;Chargill and Shakoor, 1990; Singh and Singh, 1993; Vernik et al.,1993; Palchik, 1999; Romana, 1999; Tugrul and Zarif, 1999;Kahraman, 2001; Koukis et al., 2001; Tsiambaos and Sabatakakis,2004; Yasar and Erdogan, 2004; Fener et al., 2005; Basu and Aydin, 2006; Sonmez et al., 2006a; Kilic and Teymen, 2008; Zorlu et al., 2008; Diamantis et al., 2009; Mishra and Basu, 2012;Heidari et al.,2012;Nefeslioglu,2013).In the indirect approach,the empirical equations are usually derived from simple, fast,economical and non-destructive tests such as these for determination of porosity, dry unit weight, sound velocities, and Schmidt rebound number. Another parameter for indirect/practical determination of UCS is the point load strength index. Although the point load test is destructive, this is widely used for prediction of UCS because it is quick,cheap and easy to perform both in the field and laboratory.The point load index has long been regarded as the best intermediary for determination of UCS (Romana, 1999; Basu and Aydin, 2006; Heidari et al., 2012).

In recent years, soft computing-based techniques, such as artificial neural networks (ANNs), are also gaining considerable attention for prediction of UCS (e.g. Ghabousi et al.,1991; Alvarez Grima and Babuska,1999; Meulenkamp and Alveraz Grima,1999;Singh et al., 2001; Gokceoglu, 2002; Gokceoglu and Zorlu, 2004;Sonmez et al.,2004,2006b;Karakus and Tutmez,2006;Baykasoˇglu et al., 2008; Tiryaki, 2008; Gokceoglu et al., 2009; Yilmaz and Yuksek, 2009; Dehghan et al., 2010; Sarkar et al., 2010; Cevik et al., 2011; Manouchehrian et al., 2012; Singh et al., 2012; Yagiz et al., 2012; Ceryan et al., 2013; Mishra and Basu, 2013; Yesiloglu-Gultekin et al., 2013a, b; Momeni et al., 2015; Mozumber and Laskar, 2015; Ferentinou and Fakir, 2017; Sharma et al., 2017;Mahdiabadi and Khanlari, 2019). The use of regression models to predict UCS from observed data also proved satisfactory,especially with the addition of UCS uncertainty prediction via a Bayesian approach (Wang and Aladejare, 2015, 2016; Aladejare, 2020;Aladejare et al., 2020). ANN, as a powerful tool of artificial intelligence(AI),is one of the most dynamic areas of research in advanced and diverse applications of science and engineering, especial in geotechnical engineering and rock mechanics. The application of these techniques is often preferred as these methods are relatively inexpensive and cognizant. Among these techniques, ANFIS is rapidly gaining popularity in the area of geotechnical engineering,geomechanics, mining engineering, and geophysics as it combines the advantages of ANN and fuzzy techniques and demonstrates a high prediction capacity in complex, nonlinear and multivariable engineering problems(Yilmaz and Yuksek,2009;Singh et al.,2012;Yesiloglu-Gultekin et al., 2013b; Sharma et al., 2017; Mahdiabadi and Khanlari, 2019).

Although several attempts have used AI techniques for the prediction of UCS through the physico-mechanical properties, no one has been concentrated on serpentinites.Owing to the fact that the serpentinites are usually not suitable for preparing specimens and because they are encountered in many areas over the world,more studies should be focused on them in the future.

The objective of this study is to develop a competent prediction model for UCS of serpentinites using ANNs. For this purpose, data obtained from Diamantis et al. (2009) and Diamantis (2010) were used to investigate the applicability of these techniques using ANN tools offered by the MATLAB® programming environment. The input index properties used in this study are serpentinization percentage (β), effective porosity (ne), dry unit weight (γd), saturated unit weight (γs), water absorption (Wa), ultrasonic P- and Swave velocities (Vpand Vs), Schmidt rebound number (Srn), and point load strength index (Is50), and the output parameter is the UCS.

In the following sections,development of the ANN model and its results are presented in detail. The results obtained from the ANN technique are compared to those obtained from statistical analysis in Diamantis et al. (2009) and Diamantis (2010). The improved performance indicates that the ANN model can be used for UCS prediction at the early stages of the engineering design because it is reliable, cost-effective and provides reproducible data.

2. Sample dataset description

The study area is situated in central Greece and especially in the western part of the Mount Othrys, and the area of the Mount Kallidromo. During the extensive field study, 32 block samples were collected. Laboratory core drill and saw machines were used to prepare several cylindrical specimens (3-5 per sample) and the edges of these specimens were cut parallel and smooth in accordance with ASTM D4543-01 (2001) and ISRM (2007) guidelines.After a macroscopic inspection, only the isotropic, homogeneous and unweathered(or slightly weathered)ultramafic specimens free of visible joints, cracks, fissures and other discontinuities were considered. Thirty-two thin sections were cut with the aim of determining the serpentinization percentage (β) of serpentinites(Table 1). Physico-mechanical properties including effective porosity (ne), dry unit weight (γd), saturated unit weight (γs), and water absorption (Wa) were also determined (Table 1) using the saturation and buoyancy methods in accordance with ISRM(2007).The P- and S-wave velocities (Vpand Vs) were determined in accordance with ASTM D2845(1983)using a source transducer and a receiver transducer. The wave velocities are calculated (Table 2)from the measured travel time and the distance between the two transducers.As far as the mechanical properties are concerned,the Schmidt hammer tests are conducted on specimens following ISRM(2007). In the context of rock mechanics, Srnis perhaps the most frequently used index for prediction of strength. This test is quick,inexpensive as well as mainly non-destructive and it gives an indication of the strength of the material being tested.The Schmidt hammer is a light hand-held device that consists of a spring-loaded mass inside a piston that is released when the hammer is pressed orthogonally onto a surface. Ten impacts are carried out at each specimen and the mean value is calculated (Table 2). In this research,an L-type Schmidt hammer was used.The point load test was determined according to ASTM D5731-05(2005).This test is an attractive, alternative, indirect and most commonly used way to determine the UCS owing to the ease of testing, simplicity of specimen preparation, low cost and feasibility of field application.The point load test allows the determination of the point load index(Is50). In this study, diametrical point load tests were carried out(Table 2). The UCS was determined using a uniaxial compression testing machine in accordance with ASTM D2938-95 (1995). Samples cored for this property had length/diameter ratios of 2-2.5(ASTM D4543-01, 2001). The diameters of cylindrical rock specimens ranged between 53 mm and 55 mm. Fractures created by the tests did not follow internal discontinuities and were always fresh.The mechanics tests were carried out in dry conditions for a better correlation of the results.All of them were performed at the Department of Natural Resources Management and Agricultural Engineering, Laboratory of Mineralogy and Geology, Agricultural University of Athens, Greece.

Table 2 Values of dynamic and mechanical properties of samples (Diamantis et al., 2009;Diamantis, 2010).

3. Uniaxial compressive strength(UCS)prediction using ANNs

ANNs have shown exceptional performance as a regression tool,especially when used for pattern recognition and function estimation. ANNs have a great potential in modeling the material behavior from experimental data, and the majority of the past studies(e.g.Ghabousi et al.,1991;Meulenkamp and Alveraz Grima,1999; Singh et al., 2001; Sonmez et al., 2006b; Tiryaki, 2008;Dehghan et al., 2010; Sarkar et al., 2010; Cevik et al., 2011;Manouchehrian et al., 2012; Yagiz et al., 2012; Ceryan et al., 2013;Mozumber and Laskar, 2015; Ferentinou and Fakir, 2017) on the field of geology showed that using neural network models for the prediction of strength properties concluded more accurate predictions than conventional statistical models did.

In this work, a new ANN is proposed, designed and tailored to the material presented in Section 2. The proposed ANN uses the material’s physical, dynamic or mechanical properties as inputs,and its output is the estimation/prediction of the UCS value corresponding to these properties.

3.1. Multi-layer ANN model structure

ANNs are composed of a large number of highly interconnected processing elements, the ‘neurons’, which perform linear or nonlinear ‘activation’ functions (f) and they can capture complex relationships between the inputs (X) and the outputs (Y) of a system, even when the exact nature of relationships is unknown.

Several of these neurons placed in parallel create a‘layer’and a unidirectional sequence of connected layers creates a feed-forward(FF) multi-layer ANN often called multi-layer ‘perceptron’ (MLP).The first and last layers are called ‘input’ and ‘output’ layers,respectively, and the number of neurons in them matches the number of inputs and outputs of the system under consideration.The remaining internal layers are called ‘hidden’ layers. The number of hidden layers and the number of neurons in each hidden layer are to be defined by the ANN designer,in order to represent as accurately as possible the input-output relationships.

The structure of each neuron is shown in Fig.1 and its operation is described by Eq.(1a).The output(yj)of the jth neuron on a layer is calculated by introducing the weighted(wij)sum of its(n)inputs(xi) plus its bias (bj) to its activation function (fj):

There are several activation functions(f)available,but the most common ones are the sigmoid,the hyperbolic tangent sigmoid and the linear transfer functions. In our case, we applied the second function(Eq.(2))for the hidden layer and the third(Eq.(3))for the output layer, because the hyperbolic tangent sigmoid function is a good tradeoff for any ANN,where speed is important and the exact shape of the transfer function is not,and the linear transfer function is a typical choice for the ANN output layer.

The general overall structure of an FF-ML-ANN, or MLP, which will be used in our current work and has an input layer,an output layer and two or more hidden layers, is shown in Fig. 2.

All neurons on a layer are connected to all neurons of the previous and next layers. The connections are characterized by their weights (w) and biases (b). Training an ANN is just finding these coefficients (weights and biases) in order to best fit the training dataset.

The equation y(x) that describes the above ANN model can be written using the equations of each layer(Eq.(4))in array notation(boldface), resulting in Eq. (5).

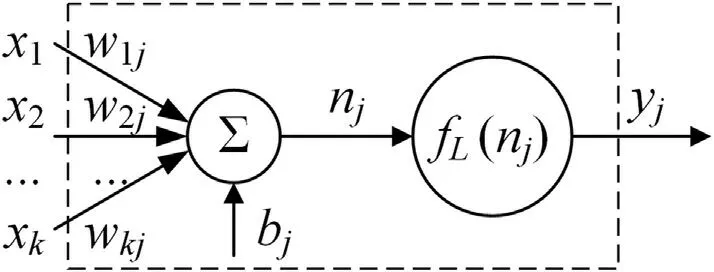
Fig.1. Internal structure of the jth neuron of layer L in an ANN.

The weights and biases in the above FF-ML-ANN or MLP are adjusted using a training,learning,or teaching algorithm.There are several training algorithms available,but the most well-known are back-propagation (BP) algorithm which is a gradient-based algorithm that has many variants and Levenberg-Marquardt (LM) algorithm which is usually more efficient but more demanding for computer resources.

In order to obtain a satisfactory performance of the models,during the data preprocessing step,the data need to be normalized by applying feature scaling, i.e. to normalize the range of the features of all input data. In our work, the minimum-maximum normalization (or rescaling) technique, as shown in Eq. (6), was used to rescale all input values in the range [0,1].

where dnormis the normalized value, dmeasis the measured value,dminand dmaxare respectively the corresponding minimum and maximum values for each parameter of the dataset.

3.2. ANN design and development

In order to estimate the UCS as the dependent variable, all the other independent variables were used as network inputs. When the problem has many uncorrelated inputs and thousands of samples available,a multi-layer ANN can have many hidden layers and many nodes per layer.But in our case,the correlation between some of the inputs as well as the low number of experimental tests currently available (Diamantis et al., 2009) requires the use of techniques for small dataset analysis(Swingler,1996;Pasini,2015)in order to obtain a simpler, more general implementation of the ANN and avoid complexity and overfitting. The ANN development is performed in two stages. First, the optimal ANN structure is selected (number of layers and number of nodes), and then its coefficients (weights and biases) are calculated.

Fig. 2. Overall structure of a multi-layer ANN with two visible (input/output or I/O) layers and two (or more) internal or hidden layers.

3.2.1. Multi-layer ANN optimal structure selection

Before designing the structure of the ANN, we have to test if there is any high correlation between various properties in the input dataset. All nine properties found in the dataset (Diamantis et al., 2009) were chosen because they relate somehow to the UCS. It is therefore inevitable for all input parameters to relate to each other.The correlation matrix of all inputs and output is shown in Fig. 3a. It is clear that some of the highly correlated inputs (e.g.above 0.93) can be removed from the dataset to reduce the complexity of the ANN structure.After trying several combinations of properties, we concluded to remove four properties (γd, γs, Waand Vs). The new correlation matrix is shown in Fig. 3b. Further reduction is also possible, but we want to also keep a level of redundancy to compensate for experimental errors and/or outliners in any of the performed tests.

After defining the input dataset to be used, and due to the low number of available samples,the detailed ANN structure is further defined using a special case of the k-fold validation for k=1,the socalled Leave-1-Out (L1O) validation test (Pasini, 2015). This exhaustive validation test is suggested due to the small number of samples in our dataset.

The L1O method was applied as follows:among the available 32 samples,one(L1O)was kept for testing,one for validation and the remaining 30 for training.The resulting ANN was tested on the one left out sample and the UCS prediction error calculated. The procedure was repeated for all 32 samples and overall mean square error(MSE)and variance were used as indications of how well the specific ANN architecture performed.To avoid any influence of the initial random values of the training algorithm,50 Monte Carlo runs were executed repeating the above procedure and the overall mean was considered more representative of the configuration.The tests for the optimal configuration started from 1 neuron in the hidden layer to 7 neurons.The process was also repeated using 2 validation samples.Both results are shown in Fig.4.It becomes clear that we obtain the best performance using 3 neurons in the hidden layer.

The resulting optimal ANN structure has an input layer,a hidden layer and an output layer of sizes 5,3 and 1,respectively(Figs.5 and 6).

3.2.2. Calculation of ANN parameters

After identifying the best structure of the ANN, the entire set was again used to identify the optimal parameters of the network.From the available 32 samples,one part is used for training the ANN and the rest for validating and testing the performance of the resulting model.

Fig.3. (a) The initial correlation matrix of all input data in Tables 1 and 2 and (b) the reduced one of the simpler model with fewer inputs (POR:Effective porosity; DRY: Dry unit weight; SAT: Saturated unit weight; WAT: Water absorption; PVL: P-wave velocity; SVL: S-wave velocity; SER: Serpentinization percentage; SCH: Schmidt rebound number; and PLS: Point load strength index).

Fig.4. Performance(MSE)of different ANN structures from 1 to 7 nodes.The hidden layer with 3 nodes gives the best validation results during L1O validation,either using(a)one or (b) two validation tests.

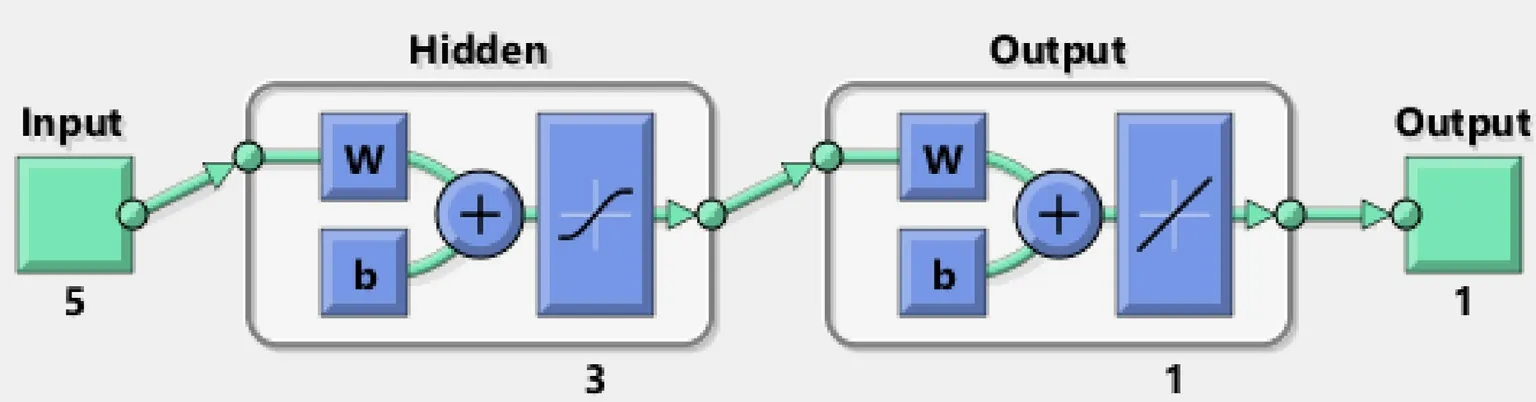
Fig. 5. Final structure of the ANN using only five test results as inputs.

Fig.6. An ANN implementation for UCS prediction using 5 of the available inputs and 3 nodes in the hidden layer.

The available data were split into 3 sections,i.e.train-validationtest (70%-15%-15%), randomly and the trained network was used to estimate the UCS values of the samples and calculate the difference(error)from the experimentally measured one.The process was repeated for 500 Monte Carlo runs. The parameter set values that produced the lowest mean error were finally selected as the most suitable ones for our case.

Fig.7 shows a plot of the MSE vs.the variance of the Monte Carlo tests as well as those with the best performance (in red color).These two tests are marked in red as they demonstrated (a) the minimum mean error and (b) the minimum error variance. The ANN with the lowest mean prediction error(a)is finally selected to represent the model for the geological data in question.

In Eq.(5),the general y(x)form of the selected ANN model was presented.The general form of Eq.(5)for our ANN model could be written in more detail in Eq. (7). The errors of the selected model(model predicted output vs. target) are illustrated in a regression plot in Fig. 8.

3.2.3. ANN simulation and test results

The selected ANN model was used to predict the UCS from the material parameter values and its results were compared to the experimental UCS values. The ANN estimated the UCS values accurately for most of the specimens and presented some minor errors in 8 of them. Another advantage of this model was that the errors were so low that the specimens were all classified into the correct category of the material(Table 3).As it is shown in Table 4,the average UCS prediction error is only 5.952% and the category classification error is 0% (i.e. absolutely correct). The prediction errors observed are mainly due to the small size of the dataset and the unequal distribution of samples between the various categories. Nevertheless, the UCS prediction accuracy of the proposed ANN is 94.048%,which is more than satisfactory compared to Diamantis et al. (2009) results (accuracy of 84.54%). Also, the material classification accuracy is absolutely correct (100%). The performance of the proposed ANN system gives us the possibility to use a small number of easier experiments and avoid destructive,time-consuming, and expensive tests.

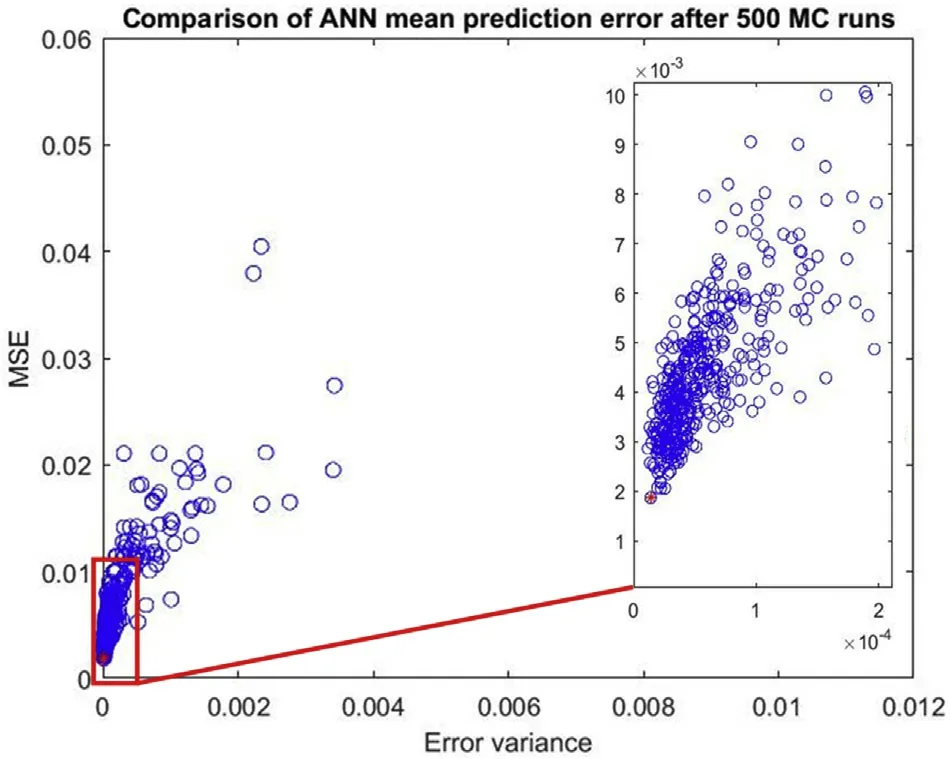
Fig. 7. Selection of the best (lowest MSE) ANN parameters to implement, after 500 Monte Carlo trial runs.

Fig.8. Scatter plot of the predicted(output)vs.measured(target)UCS values using the selected parameters.

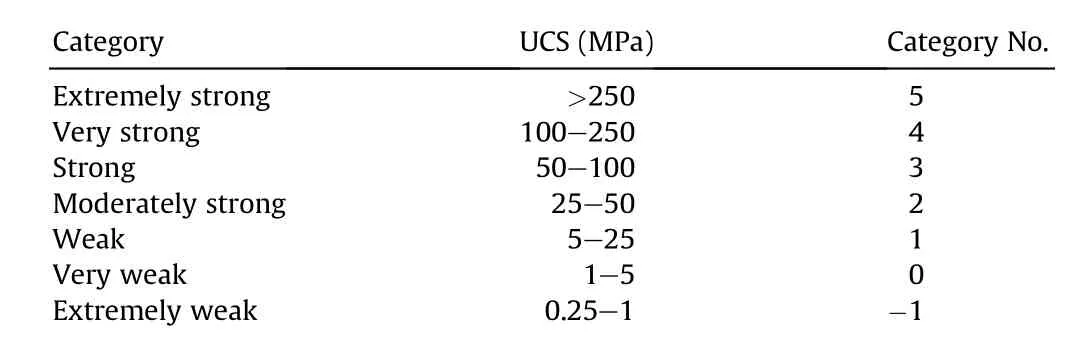
Table 3 Material category classification according to UCS values.

Table 4 UCS prediction errors and the corresponding category classification errors.

3.3. Further research and application of the ANN tool

The above presented ANN model covers only a part of the possible input combinations of material parameters that a rock mechanics practitioner may be interested of. For each different parameter combination, a different ANN must be created. This paper provides the methodology basis in order to continue developing a broader application with multiple ANNs working in parallel and covering all possible combinations of serpentinites’ properties. Our further research focuses on a more general tool that will permit any researcher or practitioner to predict the corresponding UCS value from any available number and combination of material characteristics.

4. Conclusions

The proposed ANN in this work is designed with the aim of indirectly predicting UCS through the serpentinization percentage,and physical, dynamic and mechanical characteristics of serpentinites. The developed ANN helps to avoid the UCS test, which requires high-quality core samples of proper geometry. This test is difficult to perform on weak rocks such as serpentinites. A Monte Carlo analysis is carried out to select the most suitable ANN model and its optimal structure among many candidate configurations.The suggested ANN-based easily implemented formula is found to be very accurate in predicting UCS(>94%)and especially efficient in classifying the category of the material in question (100%). Comparison of the ANN-based results to earlier works on serpentinites shows a satisfactory agreement. The proposed model predicts the serpentinites’ UCS values and their classification in a simple and cost-effective way by avoiding many destructive, time-consuming and expensive tests,which is very useful during the early stages of engineering design.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.