Application of artificial intelligence to rock mechanics: An overview

Abiodun Ismail Lawal, Sangki Kwon

a Department of Energy Resources Engineering, Inha University, Yong-Hyun Dong, Nam Ku, Incheon, South Korea

b Department of Mining Engineering, Federal University of Technology, Akure, Nigeria

Keywords: Artificial intelligence (AI)Rock mechanics Literature review Statistical method

ABSTRACT Different artificial intelligence(AI)methods have been applied to various aspects of rock mechanics,but the fact that none of these methods have been used as a standard implies that doubt as to their generality and validity still exists. For this, a literature review of application of AI to the field of rock mechanics is presented.Comprehensive studies of the researches published in the top journals relative to the fields of rock mechanics, computer applications in engineering, and the textbooks were conducted. The performances of the AI methods that have been used in rock mechanics applications were evaluated. The literature review shows that AI methods have successfully been used to solve various problems in the rock mechanics field and they performed better than the traditional empirical, mathematical or statistical methods.However,their practical applicability is still an issue of concern as many of the existing AI models require some level of expertise before they can be used, because they are not in the form of tractable mathematical equations. Thus some advanced AI methods are still yet to be explored. The limited availability of dataset for the AI simulations is also identified as a major problem.The solutions to the identified problems and the possible future research focus were proposed in the study subsequently.

1. Introduction

The quest for construction of heavy structures, underground space, resources and security over the recent decades is an inevitable demand and trend of the modernization and development of the countries around the world. High-quality development and sustainable utilization of underground space have become an international consensus. The utilization of the underground space can basically be classified into two purposes, viz. civil engineering application and mining engineering application (Sterling and Nelson, 1982; Wallace and Ng, 2016). However, the most challenging issue is the safety of the life of the workers,the users of the facility located on the surface and the underground facility.One of the key ways of achieving the safety of life and equipment in the surface and underground excavations is to ensure its stability,because excavations can lead to disturbance and redistribution of the in situ stress field of the host rock (Mahdevari et al., 2017).

Based on the degree of disturbance, surface and underground excavations can pose a major threat to the safety of personnel and equipment in and around such an excavation.Hence,the stability of surface and underground excavations has always been a great concern to geotechnical engineers(Idris et al.,2016).The stability of underground excavations, according to Idris et al. (2013), depends on the physico-mechanical properties of the rock mass, the discontinuity parameters, the groundwater condition, and the induced stresses.These parameters are generally determined using experimental and in situ measurement techniques. However, it is difficult to accurately estimate/predict the stability of underground excavation owing to the complexity of the physical system and the efforts required in determining the input data associated with geotechnical parameters (Sakellariou and Ferentinou, 2005; Idris et al., 2016). The majority of the engineering construction works and designs are carried out based on the experiences of the field engineers, but insufficient information may be provided concerning the interaction between the host rocks and the structures.

It is acknowledged that many rock mechanics problems are due to the availability of limited data, resulting in insufficient information on the behavior of the subsurface. This scenario can be described using the Holling (1978)’s classification as presented in Fig. 1. In Fig. 1, there are four regions. The first region indicates where there are good data but limited understanding. In region 2,there are limited data and good understanding; while in region 3,there are enough data and good understanding. In the fourth region, there are neither enough data nor good understanding.Therefore, the majority of the rock mechanics problems belong to regions 2-4 problems of Holling(1978)’s classification according to Starfield and Cundall (1988), while other engineering mechanics problems falls within the regions 1 and 3. However, the major problem is that the majority of the rock mechanics problems are modeled following the region 3 procedure, which is obviously inappropriate (Starfield and Cundall, 1988; Feng et al., 1997). In addition, rock mechanics problems are not only limited to the unavailability of well-defined input data in modeling but also the validation of such models and the capability to account for the inherent variability in geomaterial(Starfield and Cundall,1988).

The analytical equations for some rock mechanics problems are not available, and most of the available models cannot accommodate all the influence parameters and therefore simplified assumptions (Feng et al.,1997) are generally used. When the design engineers are supplied with incomprehensive information, their design or judgment using prior experiences on similar geological terrain would be limited. The advent of numerical modeling has abated the rock mechanics problems as it can simulate the mechanical behavior of the rock engineering structures,but there is a huge disparity between the in situ measurements and the numerical predictions (Xue and Xiao, 2017). The disparity could be attributed to the difficulty in defining suitable boundary conditions due to the lack of a comprehensive understanding of the rock mechanics problems.

Considering the inherent limitations in the traditional analytical approaches in solving rock mechanics problems and the prediction using the numerical methods, the use of data mining techniques becomes indispensable. Many data mining methods, such as statistical methods,classification and regression tree(CART),symbolic learning, case-based learning, and artificial intelligence (AI), have been used to obtain useful knowledge from the organization and analysis of raw data in civil engineering (Arciszewski and Ziarko,1992; Michalski et al., 1998; Leu and Lo, 2004). However, from the Holling(1978)’s classification,the data mining methods such as statistical methods, CART, symbolic learning, and case-based learning may not be reliable for rock mechanics problems since they are only suitable for regions 1 and 3. Hence, the most commonly used data mining approach in rock engineering and geotechnical engineering is AI.This is because many AI methods are hypothesis-free methods that do not require prior knowledge or specific experts or rules, unlike many statistical methods and the expert systems(Leu et al., 2001; Shahin et al., 2008).

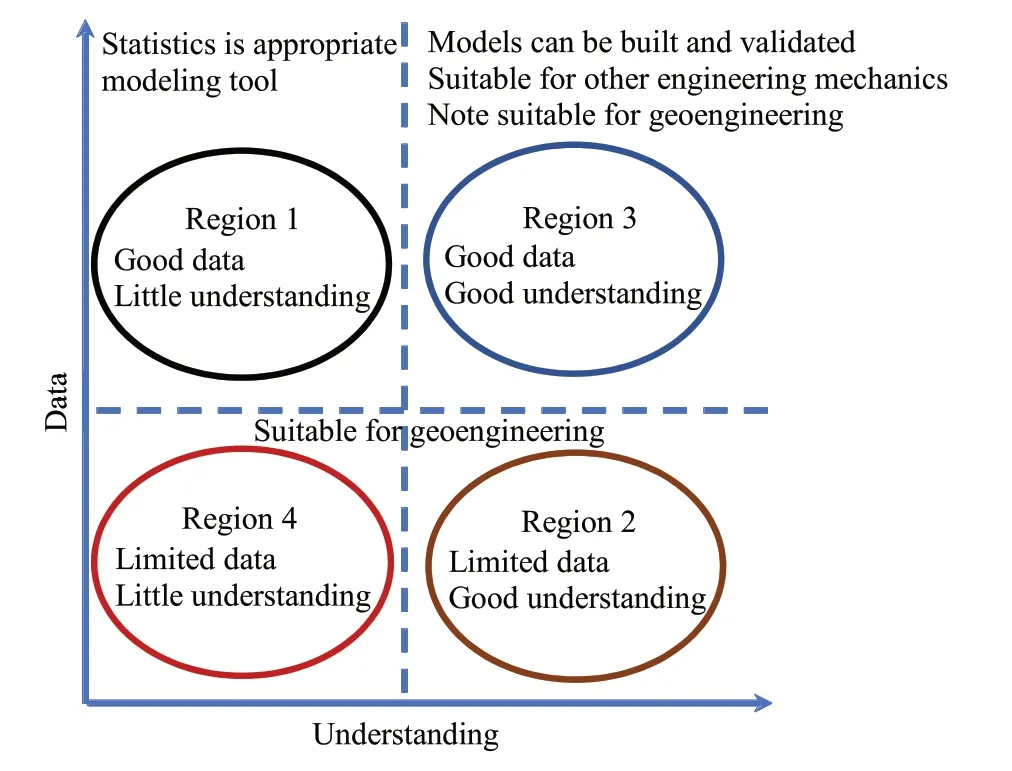
Fig.1. Modified Holling (1978)’s classification of modeling problems.

The AI method has recently gained ground in various fields of sciences and engineering owing to its ability to handle complex problems such as those encountered in rock mechanics. In AI, the pattern of operation of the human brain, the social interaction between the animals, formation, and reproduction of genes in the human being are been emulated. Hence, the approach possesses the ability to model complex problems utilizing a series of interconnectivity between the input and output parameters.AI has been used in the rock mechanics field, in the area of structural rock mechanics and rock comminution according to the classification of the Rock Mechanics Committee of the American National Academy of Sciences in 1963(Cook et al.,1966).Hence,in this study,some of the researches that have been conducted within the last decade on the application of AI in the area of rock mechanics are reviewed.The purpose of this study is to establish which of the AI approaches is most suitable and commonly used in the field of rock mechanics,and to identify the gap in the knowledge of rock mechanics that have not been filled by the existing literature.

2. Overview of artificial intelligence (AI)

AI is an aspect of computer science which deals with the simulation of human intelligence with the aid of a computer. It involves the design and building of machines that behave intelligently. These machines solve new problems, for example, visual images manipulation and processing, symbols by algorithm and heuristics from the previous learning and knowledge from experience.Although AI is basically related to computer science,it is also related to various fields of sciences such as mathematics,cognition,philosophy and psychology, and biology, and it has been recently incorporated into the field of engineering.According to Cawsey and Aylett(2009)and Carbonell(2003),tasks such as face recognition,voice recognition, navigation of heavily crowded areas and language interpretation that are extremely difficult to automate are resolved via AI.There are various branches of AI as shown in Fig.2.Among the AI approaches, the most commonly used by the researchers in rock engineering and geotechnics is the artificial neural network (ANN). ANN establishes a reasonable relationship between the input geotechnical and geometrical parameters(such as the relationship between uniaxial compressive strength (UCS)and density, Schmidt rebound hardness, P- and S-wave velocities,etc.)and the desired output based on the learning from the trained data.The overviews of some of the AI approaches commonly used in the field of rock mechanics and rock engineering are presented in Fig. 2.

2.1. Artificial neural network (ANN)

ANN mimics the human brain in the way of taking input information,processing and interpretation of the information.The ANN method developed in the 1980s is a relatively new branch of AI.In recent years,ANN is considered as one of the intelligent tools that can predict complex problems.It can generalize a solution from the pattern presented to it during training.The basic component of the ANN is characterized by its processing unit, learning rules, and connection formula (Almeida, 2002). A neural network must be trained so that a known set of inputs produces the desired outputs.Once the network is trained with enough sample dataset,for a new input of relatively similar patterns,predictions can be made based on previous learning (Khandelwal et al., 2004). ANN consists of a series of interconnected nodes.The processing ability of the ANN is stored in the weights interconnecting the nodes.The ways in which the nodes are being connected is known as ANN architecture.ANN architecture can basically be classified into two categories, viz.feed-forward network and feedback or recurrent network (Jain et al., 1996). In the feed-forward networks, there is no loop. For instance,in a multilayer perceptron,the input and output neurons are arranged into layers that have unidirectional connections between them. The feed-forward networks are static so that they produce a set of output rather than a sequence of output from a given input,while the recurrent network is dynamic.Fig.3 presents different subdivisions of the two types of ANN architecture (Jain et al.,1996). In either type of architecture, the learning process is paramount.

ANN network learns from examples or inputs presented and the output is obtained from the connecting weights and bias.Learning in the ANN palace according to Jain et al.(1996)can be expressed as the problem of updating network architecture and connection weights so that a network can perform a given specific task efficiently. Often, the network must learn the connection weights obtained from the training patterns.The performance is improved by continuous updating of the network weights (Jain et al.,1996).The ability of the ANN network to automatically learn from examples makes it unique and attractive.

Fig. 2. Branches of artificial intelligence (AI).

In order to design a learning process, there must be a model environment in which a neural network operates, that is, the information available to the network must be known. This phenomenon is termed a learning procedure. The learning procedure can either be supervised or unsupervised or reinforced (Masters,1993; Jain et al., 1996). The supervised learning is also known as associative learning; it is the learning in which the network is trained by making the input and matching output patterns available.The input-output pairs can be made available by an external teacher or be self-supervised. It resembles the conventional statistical models in a way that the model parameters are rearranged in the model calibration phase (training) in order to minimize the error between model outputs and the corresponding measured values for the given training set (Jain et al., 1996; Shahin et al.,2008). ANNs perform best when they do not extrapolate beyond the range of the data used for the training(Flood and Kartam,1994;Minns and Hall, 1996; Tokar and Johnson, 1999). Unsupervised learning is also known as self-organization; it is the learning in which an output unit is trained to respond to clusters of patterns within the input. In this archetype, the system is supposed to discover statistically salient features of the input population.Unlike the supervised learning archetype,there is no a priori definition of categories into which the patterns are to be classified but the system must rather develop its own representation of the input stimuli.

Fig. 3. Classifications of neural networks (Jain et al.,1996).

Reinforcement learning is a variant of supervised learning. In reinforcement learning,the learning machine does some action on the environment and receives a feedback response from the environment. The learning system then does the self-grading of its action; if the learning has emulated the environment very well, it will be graded good or rewarding and otherwise graded bad or unrewarding and then readjust its parameters (Jain et al., 1996;Shahin et al.,2008).There are also learning rules like the traditional expert systems,but the rules in ANNs are not humanly defined.The learning rules that are used in ANN are error-correction, Boltzmann, Hebbian, and competitive. In addition, there are learning algorithms designed or suitable for each of the ANN architecture.For single or multilayer perceptron which is the common ANN architecture in geoengineering problems, perceptron algorithms,back-propagation, Adaline, and Madaline are the associated learning algorithms (Jain et al., 1996). The variants of the feedforward network are briefly discussed in what follows.

2.1.1. Single-layer perceptron

The mode of operation of the ANN, most specifically the feedforward network trained with back-propagation of error, can be expressed mathematically, as presented in Eq. (1). For a given single-layer network(Fig.3)consisting of a scaler input and weight,the input is multiplied by the weight and then added to the bias which is more or less like weight, but it has a constant value.

where X is the input parameter, n is the argument within the network, w is the connecting weight, and θ is the bias.

Transfer or activation function (f) such as piecewise linear, sigmoid, or Gaussian is then introduced and the network output can be presented in Eq.(2).The sigmoid function is the most commonly used in ANNs.

where Y is the output of the network.

2.1.2. Multilayer perceptron

The multilayer perceptron is t he most common class of multilayer feed-forward networks, in which each computational unit employs either the threshold function or the sigmoid function(Jain et al., 1996). According to Minsky and Papert (1969), arbitrarily complex decision boundaries can be formed by the multilayer perceptron and can as well represent any Boolean function. In a multilayer perceptron,the weights are determined using the backpropagation algorithm. This has made the multilayer perceptron networks to be popular among researchers and users of neural networks. The mode treatment of the input dataset in the multilayer perceptron network can be represented mathematically in Eq.(3) (Shahin et al., 2009; Lawal and Idris, 2020).

where θjis the bias at the hidden layer;wjiis the connection weight between the input variable and the hidden layer; Xiis the input variable;Yjis the output variable;f is the transfer function;and N is the number of neurons in the hidden layer which is commonly determined using a trial-and-error approach, because there is no established rule to determine it(Rafiq et al.,2001).Although some authors related the number of neurons to the number of input and output variables and the number of training patterns(Rogers,1994;Swingler,1996; Jenkins,1997a; 1997b), this rule cannot be generalized according to Rafiq et al.(2001).Some studies also mentioned that the upper bound for the number of hidden neurons should be greater than twice the number of input parameters. According to Rafiq et al.(2001),this rule again does not guarantee generalization of the network. Hence, there is no general rule in selecting the number of hidden neurons and it is also problem-specific (Rafiq et al., 2001).

2.1.3. Radial bases function

Radial bases function (RBF) is another subset of the multilayer feed-forward back-propagation algorithm in which each of the neurons in the hidden layer has a radial function, for example,Gaussian kernel as an activation function.The location of the kernel function in the hidden layer is determined by the weight vector associated with the neurons.Both the position as well as the widths of the kernel must be learned from the pattern of the training.

Though there are many learning algorithms for the RBF network,the basic one employs the double-step learning means or hybrid learning. At the first stage, the widths and the position of kernel functions are first trained using an unsupervised clustering algorithm and then a supervised least mean square algorithm for computation of the connection weights between the hidden and output layers. A supervised gradient-based algorithm can then be used to refine the network parameters after obtaining the initial solution. One of the basic advantages of this network is that the hybrid method used in the training of the algorithm converges faster than the back-propagation algorithm in the multilayer perceptron. In terms of computation time, a multilayer perceptron is better since the required number of hidden layers is far smaller than those required in the radial based function(Haykin,1994;Jain et al., 1996). This method is not commonly employed in the prediction models such as those encountered in the field of geoengineering.

2.2. Fuzzy logic

Fuzzy logic can be viewed as a technology for the development of intelligent control and information systems. Fuzzy logic accomplishes machine intelligence by providing a means for representing and reasoning about human knowledge that is imprecise by nature(Gupta and Kulkarni,2013).Zadeh(1965)proposed fuzzy sets as an extension of the traditional set theory.The fuzzy sets allow gradual evaluation of the membership of elements in a given set described with the aid of a membership function valued in the real unit interval [0, 1]. The membership functions are usually linguistically defined. The linguistic variable is individually associated with a fuzzy number characterizing the meaning of each generic verbal term, since the linguistic variable is not directly mathematically operable (Chou and Chang, 2008). Setnes et al. (1998) mentioned that the most attractive and interesting nature of the fuzzy models in relation to other classical methods commonly used in geosciences is that they can describe complex and even curvilinear multivariable problems in a transparent way (Mishra and Basu,2013).

The fuzzy logic technique can be implemented to a real application through the following three steps as suggested by Bai and Wang (2006) and is schematically represented in Fig. 4. The first stage of implementation is fuzzification, in which the fuzzifier maps crisp data into fuzzy data or membership functions.There are different membership functions such as trapezium, triangle, bell,Gaussian, and sigmoid that can be used for the fuzzification. The second stage is the fuzzy inference process, in which the fuzzy IFTHEN rule (fuzzy implication) combines membership functions with the control rules to derive the fuzzy output. Finally, defuzzification which involves the use of different defuzzifiers such as the center of gravity(COG)and middle of maxima(MoM)converts the fuzzy outputs into crisp output.Fuzzy logic has been used in various decision making and it has also been used in solving many engineering-related problems such as quantification of environmental impact assessment by Shepard(2005),prediction of CO2cutting parameters (Parthiban et al., 2014), and study of the control of steel rod quenching after hot rolling(Giorleo et al.,1997).It has also been successfully implemented in the geoengineering field in predicting the rock property and various aspects of blasting operation.

Fig. 4. Block diagram of the fuzzy logic system.

2.3. Genetic algorithms (GAs)

Genetic algorithms(GAs)were invented by Holland(1975).It is in fact an extension and generalization of Darwin’s idea and others’ideas to assist in solving other real-world problems as it is inspired by the principles of genetics and evolution in biological populations(Coley,1999).It also mimics the reproduction behavior observed in them. The basic idea of GAs is that the offspring coming from the parents is expected to inherit a stronger character in the two parents, while the weaker traits in both parents will be suppressed which is survival of the fittest.The more fit the trait,the higher the possibility of surviving to the next generation. Hence, over a number of generations(iterations), desirable traits will evolve and remain in the genome composition of the population over traits with weaker undesirable traits. Therefore, GAs are adaptive computational methods based on the mode of operation of natural genetic systems.They exploit the historical information to forecast or speculate a new offspring with the expected improved performance (Coley,1999; Gupta and Kulkarni, 2013).

The GAs has been used extensively to solve complex design optimization problems as it can handle both discontinuous and continuous variables, nonlinear objective and constraint functions without the need for the gradient information. However, De Jong(1993) stated that applications of GAs are far more than just a robust method for estimating a series of unknown parameters within a model of a physical system. Nevertheless, GAs have been employed mostly for optimization problems in the field of engineering.Unlike other optimization tools or algorithms which begin their search spaces with a single guess, GAs are initialized with a population of guesses within the search space.The initializations of GAs are usually random and spread throughout the search space.A typical algorithm then uses three coded operators, selection,crossover and mutation to direct the population iteratively over generations towards the convergence at the global optimum. The iteration steps are based only on the objective function information and stochastic transition rules (Coley,1999).

2.4. Particle swarm optimization (PSO)

Particle swarm optimization(PSO)is one of the nature-inspired metaheuristic optimization tools based on the social behavior of some living things in searching for its needs like flocking of bird or schooling of fish. It was first proposed by Kennedy and Eberhart(1995). The mode of operation of the PSO algorithm is based on personal experience(Pbest),overall experience(Gbest)and present movement of the particles to decide their next positions in the search space. In addition, the experiences are accelerated by two factors c1and c2,and two random numbers(r1and r2)generated in interval of[0,1],whereas the present movement is multiplied by an inertia factor w varying in [wmin, wmax] (Alam et al., 2015; Alam,2016). The general form of the PSO algorithm is written as

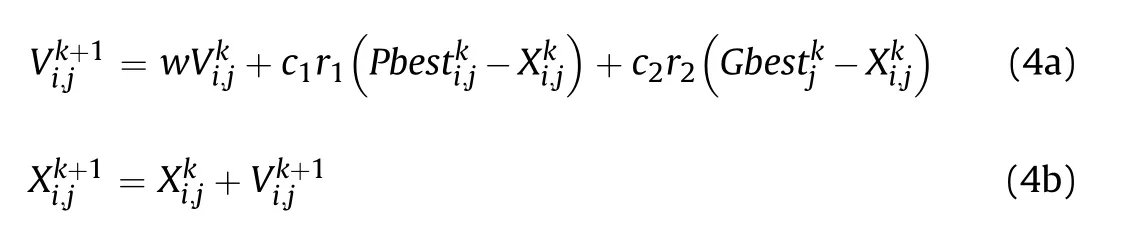
where Pbestki,jmeans the personal best jth component of the ith individual, while Gbestkjmeans the global best jth component of the best individual of the population up to iteration k. The search mechanism of PSO in the multi-dimensional search space is presented in Fig.5.PSO has also been used to solve various problems in the field of engineering. Some of the problems that PSO has been used to solve in the geoengineering field will be further explained in the next section.

Fig. 5. Search mechanism of PSO in multi-dimensional search space (Mohamed,2011a).

2.5. Support vector machine (SVM)

A support vector machine(SVM)proposed by Boser et al.(1992)is a discriminative classifier which is formally defined by a separating boundary line known as a hyperplane. SVM belongs to the general category of kernel methods (Scholkopf and Smola, 2002;Shawe-Taylor and Cristianini, 2004). A kernel method is an algorithm that relies on the data only through dot-products.Noble(2006) defined SVM as a mathematical entity, an algorithm for maximizing a mathematical function with respect to a given collection of data. In order to grasp the essence of SVM, four basic concepts, i.e. the separating hyperplane, the maximum-margin hyperplane, the soft margin, and the kernel function, must be thoroughly understood(Noble 2006).The mode of operation of the SVM algorithm is based on locating the hyperplane that gives the largest minimum distance to the training examples (Fig. 6). SVM has the ability to model complex nonlinear decision boundaries,which makes it widely embraced in different sciences and engineering fields.

3. Application of AI to rock mechanics

In the rock mechanics field (e.g. structural rock mechanics and rock comminution), various areas using AI are described below.

3.1. Comminution aspect of rock mechanics

Based on the classification of the rock mechanics by Rock Mechanics Committee of the American National Academy of Sciences in 1963 (Cook et al., 1966), drilling and blasting operation falls under the category of comminution aspect of the rock mechanics.In drilling and blasting operations, there are two expected outcomes: desirable and undesirable. The desirable outcome is attributed to the quality of the fragmentation size, heave (throw),and muck pile shape obtained after blasting,while the undesirable aspect is environmental problems (Hustrulid, 1999; Elevli and Arpaz, 2010; Raina et al., 2015). The larger percentage of the explosive energy strays to the environment during blasting and causes a series of environmental problems ranging from ground vibration, air overpressure, flyrock, toe and back-break, fumes and dust (Raina et al., 2014) (Fig. 7).

The quality of the fragmentation and the magnitude of the impacts of the blasting on the environment depend on the balance between the design parameters known as controllable parameters(i.e. burden, spacing, hole depth, hole diameter, stemming length,and sub-drill) and geological parameters known as uncontrollable parameters (i.e. UCS, point load, P- and S-wave velocities, density,porosity, and hardness). Researchers have made great efforts to quantify both the fragmentation sizes and the magnitude of the effects of blasting on the environment using various methods such as experimental methods,mathematical models,empirical models and numerical methods. Kuznetsov (1973) proposed empirical model (Eqs. (5) and (6)) for determination of the mean fragment size and its equation was later modified by Cunningham(1987)by integrating it with the size distribution function of Rosin and Rammler (1933) (Eq. (7)). The resulting equation is what is currently known as the Kuz-Ram model. The Kuz-Ram model is a famous model in predicting rock fragmentation size most importantly prior to the actual blasting operation. Nevertheless, the model can give an unrealistic prediction of the number of fines generated during blasting (Ouchterlony, 2005). The Kuz-Ram model has been modified by different studies (Kanchibotla et al.,1999; Ouchterlony, 2005; 2016; Gheibie et al., 2009) and there has been a significant improvement in prediction of the Kuz-Ram model that is most important for prediction of fines size. But the rock characteristics are not explicitly considered in the models.For the purpose of fragmentation size determination, the computeraided photographic techniques have been used in recent decades.The Wipfrag, FragScan, Split, and WIEP are available commercial software for prediction of the size distribution of fragments(Ozkahraman, 2006; Kabwe, 2018). The image analysis can be automated and could give a more accurate estimation of the fragmentation size. But their predictions are also subjected to errors that are inherent in image processing software (Maerz and Zhou,2000). A number of studies (e.g. Monjezi et al., 2009; 2010a;Kulatilake et al.,2010;Asl et al.,2018;Mehrdanesh et al.,2018)have used the soft computing/AI to predict the fragmentation sizes.Different methods that are used in computing the fragmentation size is presented in Fig. 8.

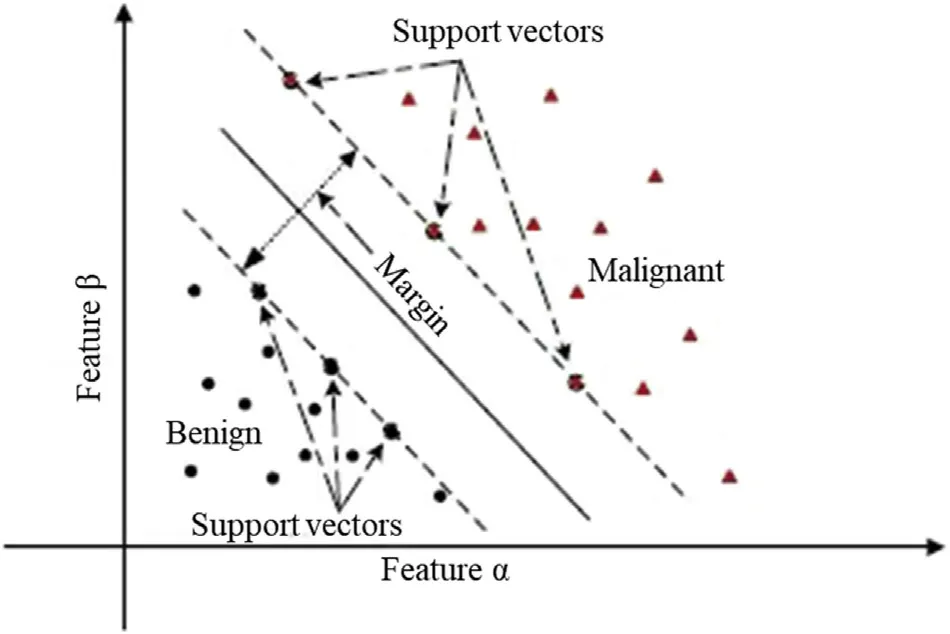
Fig. 6. Structure of SVM on a two-dimensional feature space (Wang et al., 2018).

Fig. 7. Environmental effects of blasting (Elevli and Arpaz, 2010).

where Xmis the mean size(m);A is the rock factor;V0is the volume of rock to be blasted per hole (m3); Qeis the quantity of nitroglycerin based explosive used per hole (kg), i.e. relative weight strength of explosive compared to ANFO; Rmis the Rosin and Rammler’s distribution; and u is the uniformity index given in Eq.(8a)(for the same explosive in the bottom and column charge)and Eq.(8b)(for different explosives in the bottom and column charge).

Fig. 8. Methods of rock fragmentation size prediction.

Table 1 List of some of the variants of scaled distance method.

where B is the burden (m), S is the spacing (m), D is the hole diameter(m),W is the drilling standard deviation(m),L is the total hole length (m), H is the bench height (m), and BCLis the bottom charge length.

On the other hand,mathematical,empirical and soft computing models have been proposed for prediction of the negative effects of blasting operation. For instance, the scaled-distance approach was proposed by the United States Bureau of Mining for prediction of ground vibration in a form of peak particle velocity (PPV). The frequency and PPV are the two major indices commonly used for assessing the blast-induced ground vibration. The scaled distance equation can be written as

Table 2 Existing AI models for fragment size prediction.

where SD is the scaled distance(m/kg1/2),and k and b are the field constants.

The field constants in the scaled distance equation are usually computed by fitting the field measured value with the scaled distance which is the ratio of the distance from the point of measurement to the square-root of charge per delay. Eq. (9) is sitespecific and its performance is relatively good for the site in which they are designed. This is due to the inherent variability in the rock materials which is not explicitly accounted for in Eq. (9).Since the cost of purchasing the seismograph or vibrometer and the time required to perform field measurement coupled with various permissions from the owners of the structures near the quarry site and the government policy are high, variants of Eq. (9) have been proposed by the researchers such that some numerical values of field constants have been made available. Some of the existing variants of the scaled distance model are presented in Table 1.

A great deal of effort has been made(e.g.ISRM,1992;Wu et al.,1998;Ak and Konuk,2008;Kuzu,2008;Singh et al.,2008;Nateghi 2011; Kumar et al., 2016) to examine the effects of various rock characteristics on the blast-induced ground vibration.The need for incorporation of different rock characteristics,such as density,UCS,rock quality designation(RQD),and geological strength index(GSI)which were not considered in the few available models that considered the rock characteristics, was stressed by Kumar et al.(2016). In fact, this formed the basis of their studies. Nevertheless, there are still many more rock parameters such as the rock hardness, slake durability, thermal property, porosity, Poisson’s ratio,and tensile strength and many of the blast design parameters such as burden, spacing, stemming length, hole diameter, hole depth, powder factor, and explosive properties which have not been considered in the models. The AI approach, most specifically ANN, has also been used by several researchers (see Table 4) in recent decades for prediction of blast-induced ground vibration.More parameters have been incorporated in the soft computing models. The details of the soft computing application in blastinduced vibration will be chronicled in the next section. The finite element method (FEM) has also been used by Torano and Rodriguez (2003) and Torano et al. (2006) to predict the PPV by generating artificial vibrations to study the behavior of the actual complex waves.Lu et al.(2011)also simulated the particle vibration velocities in the rock surrounding the Pubugou hydropower station in China using an equivalent method of blasting vibration based on the dynamic FEM. They acknowledged the difficulties and costs involved in simulating blasting vibration accurately using numerical computation.Wu et al.(2004)and Li et al.(2017)used dynamic finite element software to simulate the blasting vibration. Kumar et al. (2020) predicted single hole blast-induced ground vibration using a dynamic FEM.It is,however,important to note that limited efforts have been made in the use of numerical modeling for prediction of blast-induced ground vibration and this method is very safe and can approximate the field measured values using the costly equipment. In addition, various factors influencing ground vibration can also be incorporated, making this method more versatile.

Table 3 Existing AI models for flyrock prediction.

Table 4 Recent researches on the use of AI for predicting blast-induced ground vibration.

Flyrockwhich is the uncontrolled travelingof rock fragments into the region far from the blasting site has caused a large amount of damage ranging from severe to minor injury of the workers and the dwellers of the surrounding building and loss to the mining companies (Jenkins and Floyd, 2000; Verkis, 2011). One of the areas showing the influence of flyrock is presented in Fig. 9. It has been reported in the literature that flyrock is the primary cause of major injuries and fatalities among the negative impacts of blasting(Jenkins and Floyd,2000;Raina et al.,2014).Hence,the study of the flyrock remains a subject of concern to the researchers since it has to do with the safety of lives and property.Therefore,various methods such as empirical, mathematical, probabilistic, initial velocity and range, and soft computing methods (Raina et al., 2014) have been used to predict the flyrock.However,despite the recent methods for predicting flyrock,the problem still remains,though there has been a significant reduction in the incidents (Verkis and Lobb, 2007;McKenzie,2009;Rezaei et al.,2011;Stojadinovic et al.,2011;Verkis,2011;Amini et al.,2012;Kricak et al.,2012;Raina et al.,2014).The holistic review of the flyrock prediction methods can be found in Raina et al. (2014). The diagrammatic representation of the summary of the Raina et al.(2014)’s holistic review is presented in Fig.10.In this study,the recent applications of AI approaches for predicting the flyrock are reviewed in the next section.

AI presented in the previous section has been widely used in the field of mining engineering for prediction purposes. Various techniques of the AI that have been used in the fragmentation size predictions and the environmental effects of blasting operations are reviewed in this section.

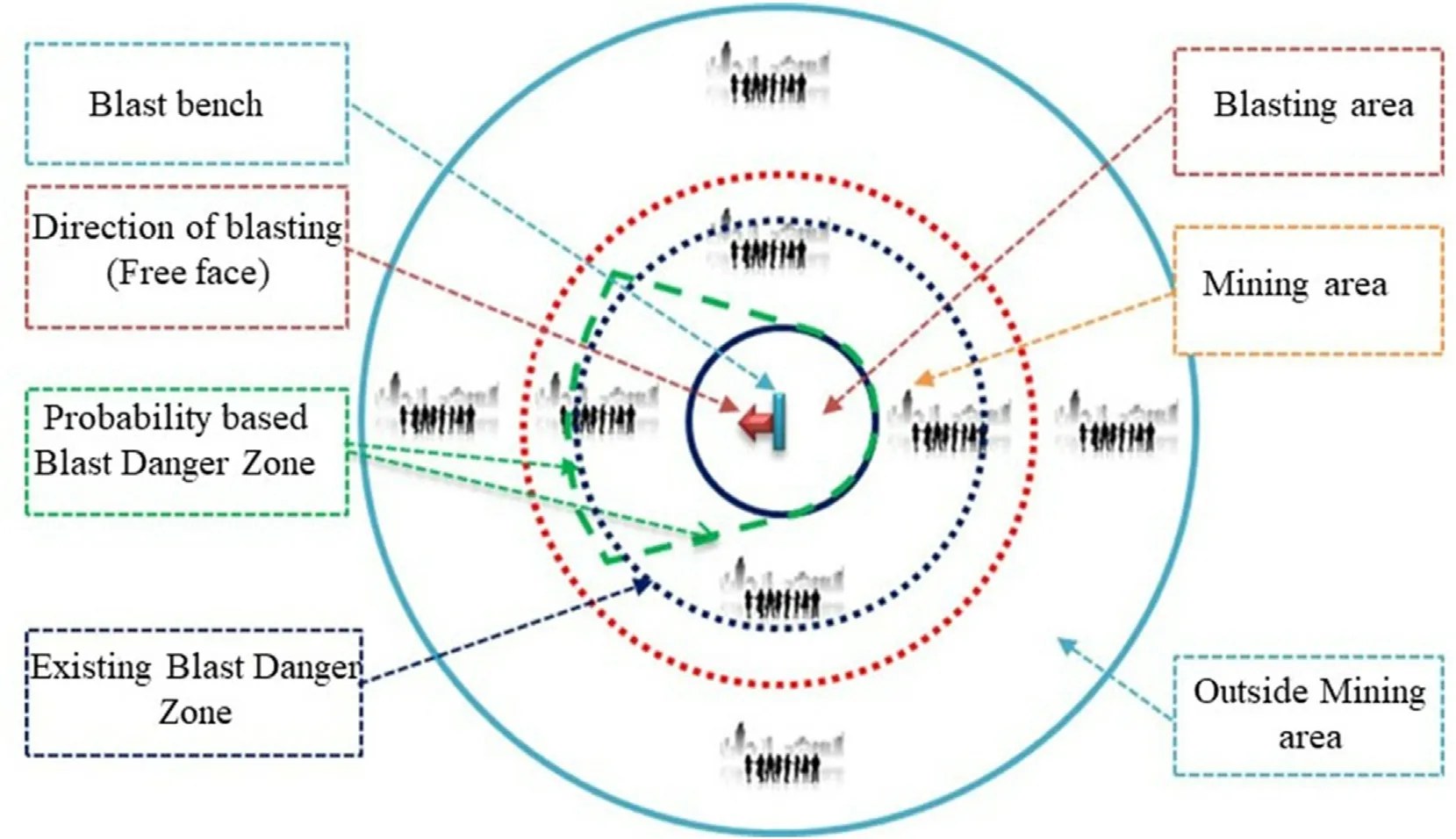
Fig. 9. Area of influence of flyrock (Raina et al., 2014).

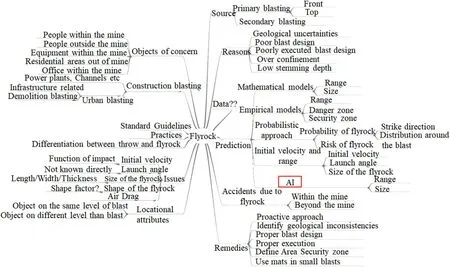
Fig.10. Summary of the Raina et al. (2014)’s holistic review of flyrock.

3.1.1. Fragmentation size estimation

The positive outcome of the blasting operation is the desired fragmentation size.The fragmentation size is important,because it determines the efficiency of the downstream operations like loading, hauling and crushing (Hustrulid,1999; Singh et al., 2005;Singh and Narendrula, 2009). The amount of energy that will be consumed in the downstream operation is significantly dependent on the quality of fragmentation size. To achieve or obtain the desired fragmentation, the mine planers must strike balance between those parameters (controllable and uncontrollable blasting parameters). The quality of the fragmentation after blasting can,therefore,be measured accurately via sieve analysis.However,due to the large volume of run-off mine, this becomes practically impossible. Hence, people resolve into the use of direct boulder counting, image analysis, and analytical models. While the image analysis is expensive, time-consuming, and unsuitable to precontrol the design of blasting, most of the field engineers rely on the analytical methods such as the Kuz-Ram model. However, this model is unreliable;hence,AI is used to predict the fragmentation size after blasting operation.The targeted output for the proposed AI models a is generally obtained from the results of the mean fragmentation size from image analysis using WipFrag, SplitDesktop, GoldSize, etc. The input parameters are some of the controllable parameters only or a combination of some controllable and uncontrollable parameters. Monjezi et al. (2012a) predicted the rock fragmentation using an ANN in Sungun copper mine in Iran.In the model, burden, spacing, powder factor, the number of rows,hole diameter,the charge per delay,stemming length,and height of the bench were the input parameters, while 20%, 50% and 80%passing were the outputs. The output of the model was compared with the multivariate regression analysis and ANN predictions were found better than the regression analysis. However, the ANN architecture selected for the model is too complex and may be difficult to transform the model into practice. The fragmentation predicted by Bahrami et al.(2011),Sayadi et al.(2013)and Ebrahimi et al.(2015)using ANN also considered some of the blasting design parameters only.

Mehrdanesh et al. (2018) evaluated the effect of rock mass properties on the fragmentation using ANN. In the proposed ANN model, 19 parameters such as UCS, tensile strength, brittleness,point load index, Young’s modulus, Poisson’s ratio, RQD, cohesion,friction angle, burden, spacing, stemming length, hole depth, hole diameter, mean in situ block size, Schmidt rebound hardness,density, and powder factor were considered as the input parameters,while the mean fragmentation size(X50)was the only targeted output. The output of the ANN model was compared with the regression analysis and decision tree. ANN was found to perform better than the other two models.However,rock properties such as P- and S-wave velocities, porosity, moisture content, and textural properties were not considered in the model. In addition,the ease of application of the model is questionable since it requires the users to perform various laboratory experiments. Also, the ANN model needs to be repeated since they are not in the form of a simple equation as in the case of a regression model.There is a high probability of not obtaining the same results if the ANN is repeated,since it is stochastic in nature.

SVM,fuzzy inference system(FIS),and hybrid AI such as adaptive neuroFIS(ANFIS),ICA-ANN,andANN-fireflyalgorithm(FFA)havealso been used for predicting fragmentation(Table 2).Nonetheless,there are other powerful AItechniques suchas PSO,GA,and the hybrid form like ANN-PSO and ANN-GA,which can render easy simple models in the form of equations that have not been used to predict fragmentation. The listed AI techniques can also be explored to ensure a sustainable and robust solution to the problem of fragmentation prediction since the traditional Kuz-Ram model is unreliable.

Majid et al. (2016) also measured the performance of the blasting fragmentation by predicting the number of boulders generated after blasting using both ANN and the multi-linear regression (MLR). The results of 33 blasts recorded in Golegohar iron ore mine in Iran were used for the model development. The input parameters in their model were joint spacing,density,UCS of the intact rock,burden,spacing,stemming length,bench height to burden ratio,and specific charge,while the ratio of boulder volume to pattern volume was the only targeted output.In the study,MLR was said to perform better than the ANN model,which is contrary to the observations in many areas of application of ANN. Dhekne et al. (2016) also developed an ANN model for measuring the number of boulders originating from the blasts in limestone quarries using 300 recorded blasting data.The input parameters in the model are hole diameter, burden, spacing, hole depth, stemming length, number of holes per row, number of rows, type of explosive and quantity of explosive. The predictions of the ANN were also compared with that of the MLR analysis conducted, and the ANN was found to perform better than MLR as expected.

Based on the reviewed studies,there is a need to re-examine the application of ANN and compare the results with the other AI techniques (e.g. ANFIS, PSO-ANN, SVM-ANN, GA-ANN, and ICAANN) to predict the number of boulders obtained from blasting as means of assessing better fragmentation. This method is also relatively cheaper as compared with the image analysis.

3.1.2. The environmental aspect of blasting

Monjezi et al. (2012b) used ANNs to evaluate the effect of blasting parameters on the flyrock in Sungun copper mine,Iran.In the model, the blasting parameters considered as the input parameters are burden,spacing,charge per delay,hole diameter,hole depth, stemming length, specific drilling, powder factor, and rock mass rating(RMR),while the only targeted output was the flyrock.Different ANN architectures and training algorithms were tried and the one that gave the best performance was selected. The ANN output was compared with the predictions of the traditional mathematical model by Lundborg(1974)and Lundborg et al.(1975)and the MLR statistical model. ANN prediction was found to be closer to the field measured flyrock. In the model, the proposed ANN model was not presented in the form of a tractable equation that can be used in the quarry with similar rock characteristics. In addition,many of the rock properties that influence the formation of flyrock such as P- and S-wave velocities, rock density, slake durability index, modulus of elasticity and Poisson’s ratio are not considered. Trivedi et al. (2014) also predicted the blast-induced flyrock in the Indian limestone mines using the ANN and the multivariate regression analysis. Blast design and geotechnical parameters,such as linear charge concentration,burden,stemming length, specific charge, UCS, and RQD, have been selected as input parameters and flyrock distance used as an output parameter in their model. Those parameters were also used as the dependent and independent variables in the multivariate regression analysis.The results predicted using ANN were compared with the field measured, multivariate regression model predicted and the calculated flyrock. ANN was found to outperform the other methods compared.

Several studies(e.g.Monjezi et al.,2010a;Monjezi et al.,2013a;Ghasemi et al., 2014) have also used ANN for the prediction of flyrock in various mines.A hybrid form of ANN such as ANFIS,ANNPSO, ICA-ANN, and ANN-GA has also been used to predict flyrocks by many studies(e.g.Monjezi et al.,2012b;Armaghani et al.,2014a,2015a,b;Marto et al.,2014).Other AI techniques such as SVM,FIS,and PSO have also been used by very limited researchers (Rezaei et al., 2011; Amini et al., 2012; Khandelwal and Monjezi, 2013a;Hasanipanah et al., 2016). The recent AI-based models developed for the flyrock predictions are presented in Table 3.

For the case of blast-induced ground vibration,AI methods have been used to predict the ground vibration in terms of PPV and frequency in various mining companies. Gorgulu et al. (2013)investigated the blast-induced ground vibrations in the Tulu Boron open-pit mine in Turkey using the ANN. The study indicated that the magnitude of the blast-induced ground vibration is affected by parameters such as the physico-mechanical properties of the rock mass, characteristics of the explosive, and blasting design parameters. The proposed model was based on distance from the measuring station to the blasting point, the maximum charge per delay, number of holes, hole depth, stemming length,spacing,burden,and other parameters such as RMR,resistivity,and P-and S-wave velocities obtained from the site investigations.The prediction of the ANN model was found to be closer to the measured PPV as compared to the traditional scaled distance approach.The limitation of the proposed model is that it cannot be applied to the mines with similar characteristics, since they were not presented in the form of a tractable mathematical model(Shahin et al., 2009; Lawal and Idris, 2020). In addition, rock properties and design parameters such as Young’s modulus, Poisson’s ratio,rock density,hardness,hole diameter,total charge,and sub-drill depth were not included in the proposed model.

Saadat et al.(2014)predicted blast-induced ground vibration in an iron ore mine in Iran using a four-layered feed-forward backpropagation multilayer perceptron ANN. In the proposed ANN model,the maximum charge per delay,distance from blasting face to the point of monitoring,stemming length,and hole depth were taken as inputs, while the PPV was considered as output. The performance of the proposed ANN model was compared with those of the traditional scaled distance approach and the MLR model proposed in their study.It was found that ANN performed better than the other models.In addition,the physico-mechanical properties of the rock were not considered in the model and the intensity of the blast-induced ground vibration was attributed to the rock properties.The complex ANN architecture selected for the model may be unnecessary, because a three-layered ANN network is enough to give a reasonable prediction (Bishop, 1995; Onifade et al., 2019;Lawal and Idris, 2020).

Alvarez-Vigil et al.(2012)used ANN to predict the blast-induced ground vibration in terms of PPV and frequency in an open-pit mine in Spain. The input parameters for the ANN are RMR, relative arrangement of the blast and the control point, distance between the blast and control point, blast hole diameter, blast hole length,spacing between blast holes,burden,instantaneous charge,total charge, number of blast holes, and explosive detonation velocity.The comparison showed that ANN performed better than the MLR model. In the model, some of the physico-mechanical properties(Young’s modulus,Poisson’s ratio,density,porosity,P-and Swave velocities, hardness, and slake durability index) of the rock were not considered and the models were not in the mathematical form.

Khandelwal and Singh (2009), Mohamed (2011b), Gao et al.(2002), Amiri et al. (2016) and Nguyen et al. (2019a) have also used ANN to predict the blast-induced ground vibration in terms of PPV. Other AI methods that have been used in predicting blastinduced ground vibration are FIS (Mohamed, 2011b), SVM(Hasanipanah et al., 2015a; Mohammadnejad et al., 2012; Nguyen 2019; Shang et al., 2020), and PSO (Hasanipanah, 2017a). The hybrid AI methods such as ANFIS (Iphar et al., 2008; Armaghani et al., 2015b, c), PSO-ANN (Armaghani et al., 2014a; Hajihassani et al., 2015a), FFA-ANN (Shang et al., 2020), ANFIS-PSO (Ghasemi et al., 2016), and ANN-KNN (Amiri et al., 2016) have also been used by different studies to predict the blast-induced ground vibration.However,most of the proposed models did not consider the physico-mechanical properties(such as UCS,Young’s modulus,Poisson’s ratio, density, porosity, Schmidt rebound hardness,slake durability index, and thermal conductivity) of the rock and some design parameters (such as burden, spacing, hole diameter, stemming length, bench height, sub-drill, explosive type, quantity, velocity of detonation,and density of explosive),although the models have demonstrated the applicability of AI methods for prediction of blast-induced ground vibration. The summary of the various AI approaches that have been used in blast-induced ground vibration predictions is presented in Table 4.

Back-break, over-break, and air overpressure have also been investigated extensively in different studies (e.g. Monjezi et al.,2010c; 2012b; Khandelwal and Kankar, 2011; Mohamad et al.,2012; Sayadi et al., 2013; Khandelwal and Monjezi, 2013b;Armaghani et al., 2015b; Ebrahimi et al., 2015; Hajihassani et al.,2015b; Hasanipanah et al., 2015b; Saghatforoush et al., 2016;Hasanipanah et al., 2017b; Koopialipoor et al., 2019) using AI approach.A detailed review of blast-induced ground vibration and flyrock has been discussed, and the AI techniques used for their predictions have similar procedures with different areas of applications.

3.2. Structural rock mechanics

The structural aspect of rock mechanics according to Cook et al.(1966) is concerned with the stability of engineering structures in which the materials are predominantly rocks. Stability is a very imperative issue in mining/rock engineering, because it concerns the safety of the life of the workers,the users of the facility located on the surface and the underground facility.One of the key ways of achieving the safety of life and equipment in both surface and underground excavation is to ensure its stability. For instance, a threat can be posed to the surface mining workers, equipment or the building at the cliff of the surface excavations if slope fails.The assessment of the stability of underground mines and the slopes in surface mines is complex, because it depends on the rock characteristics which are not well understood in most cases.

The rock characteristics play an important role in the planning of both open-pit and underground mines, design of support,excavation strategy and production, coal bed methane production,fracking for CBM extraction,and viability of CO2sequestration(Roy and Singh, 2019). Hence, a fast and accurate assessment of these characteristics is required in both the field and laboratory. However,it is very tedious,time-consuming,and costly to carry out the analysis in the laboratory or in the field.In addition,a high level of expertise is also required. As a result, researchers have proposed some empirical/mathematical models to estimate some of the mechanical properties of the rock indirectly or via some simple parameters that can be measured in situ or in the laboratory.However,the majority of these models are two-parameter models that have neglected the effects or contributions of other parameters on the predicted rock properties, whereas those that considered multiple parameters in their models used a simple regression method but the method cannot handle the inherent variability in rock engineering materials,making their models site/case-specific.Hence, the use of the data mining approach, most specifically AI,becomes imperative to handle the variability in the rock properties.In addition, it enables the formulation of generalized models that can be applied to other fields with similar properties once the model has learned those data during the training (Onifade et al.,2019; Roy and Singh, 2019).

This section presents the efforts that have been made by different studies in the use of AI to predict the physico-mechanical properties of rocks,and its application in other aspects of structural rock mechanics such as stability analysis and rockburst analysis has been discussed in detail in what follows.

Table 5 Recent researches on the use of AI for predicting mechanical properties of rock.

3.2.1. Predictions of mechanical properties of rock using AI

Roy and Singh (2019) predicted the deformation properties(Young’s modulus and Poisson’s ratio)of Indian coal using ANN and a hybrid form of ANN known as ANFIS.They have used UCS,tensile strength, shear strength, and P-wave velocity as the input parameters in the models,while the Young’s modulus and Poisson’s ratio were the output parameters. The performances of their proposed ANN and ANFIS models were compared with the traditional MLR model that was also proposed in their study. ANFIS gave the best performance followed by ANN and then MLR.It is obvious that the input parameters used in developing the proposed models are insufficient as parameters like density, porosity, shear modulus,and shear wave velocity were not included.In addition,the limited data used in developing the models may not be enough for the generalized model.The models developed were not in the form of a mathematical/empirical model that can be used by the intending user(s) for estimation of the deformation properties.

Torabi-Kaveh et al. (2015) predicted the UCS and Young’s modulus of limestone samples obtained from different dam sites using ANN.In the model,the P-wave velocity,density,and porosity were the input parameters,while the UCS and E were the targeted output parameters. The prediction of the ANN model was compared with the regression model conducted in the study.ANN has the highest coefficient of determination as compared with the regression model.Roy and Singh(2019)indicated that there are still many parameters that have a relationship with UCS and E that were not considered in the proposed model.In addition,though the ANN model performed better than the MLR model, the practical application of the ANN prediction by the field users may not be possible since it is not in the form of the equations like the regression model.

Dehghan et al. (2010), Manouchehrian et al. (2012), Rabbani et al. (2012) and Torabi-Kaveh et al. (2015) have used ANN to predict the UCS and Young’s modulus of rocks. Besides ANN, other AI methods such as fuzzy logic,GA,and hybrid form of ANN like ANFIS,GA-ANN, and PSO-ANN have been used (e.g. Singh et al., 2012;Rezaei et al., 2014; Mohamad et al., 2018) to predict the UCS and Young’s modulus. These parameters are considered important in the rock engineering design and different models have been proposed in the literature for their predictions considering various parameters. Hence, it may be difficult to compare the models’performances since they were established using different input parameters and different rock types.

All the models have shown that AI approaches are more powerful than traditional regression analysis.However,in terms of the ease of practical use, a larger percentage of the models presented in Table 5 did not provide a tractable mathematical formula that will eliminate the need to perform the simulation of the AI when such a model is required for the rock with similar characteristic. This issue requires urgent attention; otherwise, the soft computing models would be a mere academic exercise with little or no practical application. Some of the models developed are presented in Table 5.

Kaunda and Brian (2016) also used ANN to predict the brittleness of limestone, metamorphic and igneous rocks using the rock type(igneous,metamorphic or sedimentary),unit weight,P-and Swave velocities, dynamic Poisson’s ratio, dynamic Young’s modulus, and Lame’s constant as the input variables. The model showed a better fit when compared with the existing study and the MLR. However, the model may not attract practical attention,because the ANN model was not presented in the form of a simple mathematical model like the existing model and not all the parameters that influence the investigated rock property were considered in the model. Hussain et al. (2019) also predicted rock brittleness using PSO and ICA. The Schmidt hammer rebound number, wave velocity, density, and point load index (Is(50)) were selected as the independent (input) parameters and the BI values are considered as the dependent(output)parameter.The linear and power models of PSO performed better as compared with the ICA.Hussain et al. (2019)’s model shows better performance when compared with Kaunda and Brian (2016) with respect to the coefficient of correlation. The models are also in the form of simple mathematical equations that make their applicability visible,although the study also neglected some rock parameters in the proposed model. Yagiz and Gokceoglu (2010) also used an FIS to predict rock brittleness based on the combination of rock properties such as UCS, Brazilian tensile strength, and unit weight of the rock. The obtained fuzzy predictions were compared with the nonlinear regression analysis results. The predictions of nonlinear regression are closer to the measured value in their study. In general,limited work has been conducted to predict the brittleness of rock using AI contrary to the case of UCS and deformation properties. Hence, there may be needed to explore more AI techniques such as SVM,ANFIS,ANN-PSO,and GA-ANN for more accurate and robust models for the rock brittleness index prediction.

3.2.2. Stability predictions using AI

The accurate estimation of the stability of rock or soil is a very difficult problem in rock engineering because of the behavior of interactive parameters (such as cohesion, shear strength, friction angle,slope height,slope angle,water pressure,and seismic force)that is yet to be fully understood and the difficulty involved in determining these parameters. Hence, stability analysis is one of the multivariate dynamic systems which always poses a challenging and demanding problem (Sakellariou and Ferentinou,2005). For the slope stability commonly experienced along with the road cuts or surface excavations, the traditional method of assessing the stability of the rock or soil slopes is limit equilibrium approach. In assessing the slope stability using this approach, one needs to compute the factor of safety (FoS) which is the ratio of resisting force to the driven force (Das, 2008; Abdalla et al., 2015).

The traditional approaches used in estimating the slope stability are based on simplified assumptions to render their equations statically determined.Hence,the suitability of the limit equilibrium approach will depend on how good the underline assumption is.On the other hand, numerical methods (analytical methods, basic numerical methods,FEM,boundary element method,distinct element method, hybrid methods, extended numerical methods, etc.) have also been used to assess the stability of slopes (Jing and Hudson,2002; Jing 2003; Cheng et al., 2007; Verma et al., 2016). However,according to Jing and Hudson(2002)and Jing(2003),all numerical methods are aimed at one-to-one mechanism mapping in the model.

The term one-to-one mechanism mapping according to Sakellariou and Ferentinou (2005) depicts the direct modeling of geometry and physical mechanisms, either specifically or through equivalent properties, but AI approaches are none the one-to-one mapping. This characteristic makes them suitable for solving various problems in rock and soil mechanics.In view of this,various studies have used AI,mostly ANN,to assess the slope stability and stability of excavations in underground mines.

Verma et al.(2016)assessed the stability of a road cut along the landslide-prone area using the FEM and ANN. The FoS for various combinations of soil/rock parameters was computed with Plaxis 2D software using the strength reduction method. Then the ANN simulation was performed in the model using slope angle, pore pressure, cohesion and friction as the input parameters and the obtained FoS via FEM as the targeted output.The obtained FoS via the ANN was compared with that of the FEM and they were found to be very close, indicating that ANN is suitable for assessing the slope stability.

Abdalla et al.(2015)also predicted the minimum FoS against the slope failure in clayey soils using the ANN.The slope angle,friction angle and stability number (c/(γH)) were used as the input parameters in one of the two architectures of the ANN model, while slope angle, friction angle, cohesion and unit weight were used as the input parameters in the second architecture. The targeted outputs in the two ANN models were FoS values which were obtained from four well-known methods of Fellenius (ordinary),Bishop, Janbu and Spencer. It was observed that the predicted FoS values using the two architectures were very close to that computed by each of the corresponding four widely used limit equilibrium methods.

Ai and Zsaki (2017) assessed the stability of homogeneous slopes under dynamic load through tracked cranes using an ANN approach.The parameters for the construction and training of their ANN were obtained from the slope stability models performed using Monte Carlo sampling.Their proposed ANN model is capable of predicting the FoS of a loaded slope and the location of the critical failure surface with relatively low accuracy. Hence, the applicability of the AI to slope stability prediction has been demonstrated.

Aside from the slope stability analysis, ANN has also been applied to the stability analysis of underground mines.For instance,Idris et al. (2015) stochastically assessed the stability of the underground mine pillar at Laisvall mine using the ANN. Mahdevari et al. (2017) predicted the stability of gate roadways in longwall mining using the ANN.Katkuri et al.(2019)used a neural networkassisted analysis for longwall gate road stability based on measured roof convergence data.ANFIS was also used by Farid et al.(2013)to predict the roof fall in a coal mine. Studies carried out have also shown that the AI can be used in assessing the stability of slopes and underground mines, but many of the variants of AI methods have not been used in performing this task. Hence, a more robust assessment of the stability of the slopes in both surface and underground mines is required in relation to the safety of lives and property. Some of the recent AI applications to the stability problems are presented in Table 6.

Table 6 Recent researches on the use of AI for stability prediction.

3.2.3. Rockburst prediction using AI

Rockburst is a major issue of concern in mining engineering and rock engineering, most especially in a deep underground mine because of various degrees of injury that can be sustained by the workers and the destruction of the equipment as a result of its occurrence.This term is commonly used to describe various levels of rock failures, which are commonly experienced in tunnels,shafts, caverns and mines (Dowding and Andersson,1986; Kaiser et al.,1996; Blake and Hedley, 2003; Li et al., 2017a, b; Zhou et al.,2018). Rockburst occurred in almost all the existing underground constructions and mines in the whole world (e.g. South Africa,China, Chile, USA, Canada, Norway, Russia, Sweden, Switzerland and Korea) (Zhou et al., 2018; Pu et al., 2019). Due to the complex nature of the rockburst, the phenomenon is yet to be understood due to its dynamic and nonlinear multivariate nature (Hoek and Brown,1980). In general, rockburst methods of evaluation can be categorized in two ways: rockburst classification and rockburst potential prediction (Zhou et al., 2018). Due to the lack of detail information and noisy data with regard to studies on rockburst,the traditional means of assessing rockburst cannot capture the model and parameter uncertainty. This has motivated researchers to explore the use of AI to model/capture the uncertainty in the rockburst prediction parameters(Zhou et al.,2016;Pu et al.,2018).Some of the recently published work on rockburst prediction is discussed as follows.

Jia et al.(2013)predicted rockburst using the PSO algorithm and the general regression neural network (GRNN) model. In their approach, ANN was used to build the regression model using the existing rockburst database and the PSO was used to optimize the input parameters of the network to minimize the adverse effect of a human-induced factor in the model construction. There are four input parameters in the proposed PSO-GRNN model, including tangential stress on the boundaries of tunnels or caverns, UCS,uniaxial tensile strength of the rock,and elastic energy index of the rock.Those parameters were obtained based on energy theory and data obtained from 26 practical cases. The proposed PSO-GRNN applicability was tested in the Cangling tunnel and Dongguashan copper mine and was found to be successful.

Zhou et al. (2012) used the SVM to evaluate long-term prediction of rockburst. In the model, buried depth H, maximum tangential stress of rocks,UCS and uniaxial tensile strength of rocks,stress coefficient, rock brittleness coefficient, and elastic energy index were the input parameters. To further enhance the performance of the SVM, GA and PSO were used to optimize the hyperparameters of the SVM. A total of 132 datasets were used to evaluate the rockburst. It was found that GA and PSO optimized parameters can enhance the search rate of SVM parameter optimization. The proposed model is robust and could serve as an important model in rockburst evaluation. Zhao and Gross (2017)also predicted rockburst using the SVM based on the case history data.The proposed model can be used in predicting the rockburst in the mine with similar rock characteristics(Pu et al., 2019).

Zhou et al. (2016) evaluated the performances of various AI approaches such as ANN, SVM, support vector regression, and adaptive-neuro fuzzy in rockburst prediction.The performances of the different methods were evaluated and compared. The algorithms and different rockburst indicators were used as the input features and their training sample sizes were different. Hence, the bases of the comparison of the model performances may be faulty since the models were not built based on the same parameters.

He et al.(2015)also predicted the rockburst using ANN and SVM based on the laboratory tests database. The study predicted the rockburst maximum stresses and rockburst risk index using two groups of data, each for the rockburst maximum stresses and rockburst risk index. The depth, UCS, deformability modulus,loading,and unloading face horizontal in situ stresses and vertical stress due to overburden are the data in group 1 used for the rockburst maximum stress prediction. While in the second group,the percentages of clay,quartz,feldspar,calcite,carbon,and volume of the sample were added to the first group data.

For group 3 in the case of rockburst risk index, the depth, UCS,deformability modulus,rockburst maximum stress,and stress ratio were used, and for group 4, percentage of carbon was added. The results obtained using ANN and SVM were compared with that of MLR analysis. SVM performed better than the remaining two models for groups 1 and 2 in the rockburst maximum stress prediction.Whereas in the rockburst risk index,SVM performed better in group 3, while ANN performed the best in group 4. The study indicated that only MLR provides an equation relating to the output and the input variables.Hence,the practical applicability of the best performing model is uncertain.

This review has shown that AI has been used in predicting the rockburst which is a major catastrophic hazard in underground constructions and mines. More details on the application of machine learning in rockburst applications can be found in Zhou et al.(2018) and Pu et al. (2019). Notwithstanding, there are other AI techniques, especially the hybrid ones, that have not been used in solving the problem of rockburst. The performances of the AI techniques have been established in different studies, but the models developed are not presented in a simple equation form like the MLR. Some of the recent researches that employed AI in predicting rockburst are delineated in Table 7.

4. Discussion, conclusion and future direction

Researches have shown that rock mechanics/geoengineering problems are highly characterized with limited data and knowledge,and site-specific.Therefore,AI is a promising tool to simulate such a relationship, because it does not require any prior knowledge about the kind of relationship that exists between the predictors and the predicted variables. This is one of the main advantages of AI over traditional empirical and statistical methods.However,there are still some problems with the application of AI in rock mechanics problems.

Table 7 Recent researches on the use of AI for rockburst prediction.

For the fragmentation analysis,ANN,SVM,ANFIS,FIS,ANN-FFA and ICA-ANN have been used to predict the fragmentation size based on the controllable parameters only or with both uncontrollable and controllable parameters. Though the predicted fragmentation size using AI is far better than the traditional Kuz-Ram model as evident in the literature,the practical applicability of the AI model is still an issue of concern. This is because the AI-based models are not in the form of simple equations that can be used by the field engineers,while designing the blasting rounds thereby necessitates the simulation of AI for each blasting which is obviously impossible.In addition,the AI method has never been used to predict the distribution of the fragmentation size. There are still more AI methods that have not been used to develop models with consideration of design and rock parameters in the existing works.This can further be investigated in future studies.

In the case of flyrock prediction, many AI methods have also been used for its prediction as presented in Table 4.However,those models also have the same drawback as observed in the case of fragmentation size.But PSO was used to predict the flyrock and its prediction was reported in the form of the tractable mathematical model,although many of the design and rock parameters were not included in their model.In addition,more robust AI that can handle the complex variability in the input parameters should be explored and simplified into a simple form.This is also applicable to the case of blast-induced ground vibration.

For the predictions of the mechanical properties of the rock,ANN,FIS and a hybrid form of ANN are mostly used.However,there are many mathematical models that are available for the quick estimation of the strength parameters,though they are not reliable.AI methods offer more accurate results, but their practical applicability is still uncertain,since there is a need for repetition of such a model before it can be applied. This requires some level of expertise which may be difficult to obtain among the targeted users of the model.

In rockburst prediction,shallow machine learning such as SVM which can only establish a relationship between the parameters that cause rockburst and the rockburst index has been used by many researchers. This method is incapable of capturing the inherent and spatial variability within the data.Therefore,there is a need to explore a deeper machine learning method for the accurate prediction of the rockburst phenomena in underground construction and mines.

In summary,many studies have used AI to unravel various rock mechanics problems as discussed in this review, but there are still some problems in their applications ranging from insufficient data to non-availability of a simple form of the models for the intending users.Hence,future researches should be tailored towards the use of advanced numerical modeling methods like FEM and DEM to simulate the field situations and generate enough data for the input into the AI.Bayesian approach coupled with Monte Carlo sampling techniques(Wang and Aladejare,2016;Aladejare and Akeju,2020)can as well be used to generate reliable input datasets for the AI model. This can enhance generalization of the AI models and eliminate the problem of non-availability datasets. Monte Carlo sampling application in AI was demonstrated by Ai and Zsaki(2017). This highly coupled versatile model will be very useful in the future, most importantly in various aspects of mining engineering that are very difficult to acquire data due to threat to life and cost of equipment.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This work was supported by Korea Research Fellowship Program through the National Research Foundation of Korea funded by the Ministry of Science and ICT (Grant No.2019H1D3A1A01102993).