数学解题应遵循“多想少算”原则①

卓 斌

(南京师范大学附属中学秦淮科技高中 210007)

1 问题的提出

笔者首先引导他运用通解通法来解决该问题．

解法一由于函数表达式中有|x|，

再令3x2-1=t(t>-1)，

当t=0时，g(t)=9；

当且仅当t=2时，等号成立；

当且仅当t=-2时，g(t)有最大值为0，显然不符合题意．

反思解题过程，我们认为上述解法固然是解决这一问题的“通解通法”，但是给人以“只顾埋头拉车，没有抬头看路”的感觉．再反复观察函数f(x)解析式的结构特征，笔者发现：该分式函数的分母不太好变形，但是分子1+3x2可以变形为2x2+(1+x2)，从而给出如下解法．

解法二因为x≠0，所以

当且仅当2x2=1+x2，即x=±1时，

通过对比这道题的两种解法，深切地感受到数学解题一定要多观察、多联想、多思考，才有可能少走弯路，少运算，少出错．

2 对于“多想少算”的理解

拿破仑认为：在做一件具体的事情的时候，最笨的就是勤奋但不聪明的人，在事情都没有搞清楚前就忙于勤奋的人，只会是添乱的人．所以说，在做事情前一定要想清楚后再做．郑毓信教授指出：这显然又是当前应当努力纠正的一个现象，学生一直在做，一直在算，一直在动手，但就是不想！这样的现象无论如何不应再继续了．他还认为：判断一堂数学课成功与否的基本标准，无论教学中采取了什么样的教学方法或模式，应该更加关注自己的教学是否真正促进了学生更加积极地去进行思考，并能逐步学会想得更清晰、更全面、更深、更合理．

笔者认为，应将“思维发展”看成是数学核心价值与学科素养的基本涵义．数学解题教学应遵循“多想少算”原则，即在认真审题，反复观察的前提下，首先要开动脑筋，广泛联想，大胆猜想，充分想象，然后再动手做题，谨慎计算，简练书写，边想边算．只有想的充分，才能算的简约；只有发挥直觉思维的作用，才能尽量减少繁琐的运算．“多想少算”应成为解题教学的一个响亮的口号！

3 例谈数学解题中的“多想少算”

高考数学试题一直将“多考点想，少考点算”作为一条基本的命题理念，在近年的高考试题中得到了充分的体现．因此，考生在面对一道高考试题或者模拟试题时，一定要坚持“多想少算”．笔者认为，实现“多想少算”有三种基本做法：先想后算，边想边算，算后再想．

3.1 先想后算

先想后算是指对于一些常规数学问题，在动手做题之前，一定要先想一想，预测大致的解题路径，然后再动手实施解题计划．

案例1在△ABC中，已知a2+b2+2c2=8，则S△ABC的最大值是．

先建立平面直角坐标系，

下面有多种方法可以求出S△ABC的最大值．

思路三：利用海伦公式.

设a=y+z，b=x+z，c=x+y，

8=(y+z)2+(x+z)2+2(x+y)2

=3x2+3y2+2z2+4xy+2yz+2xz

=2z(x+y+z)+3(x2+y2)+4xy

≥2z(x+y+z)+10xy

3.2 边想边算

边想边算是指对于一些新颖或者困难问题，答题者一时难以设计出完整的解题路径，只能采取“摸着石头过河”的方式，一边想一边做，一边做又一边想，不断地调整、修改、优化解题路径，采取“步步为营”策略．

案例2已知{an}是等比数列，Sn是其前n项和．若a3=2，S12=4S6，则a9的值为．

思路分析：本题属于数列中的条件求值问题，两个条件“a3=2，S12=4S6”，利用“基本量法”，理论上肯定能够解答．但是等比数列中的计算问题需要分类讨论，更需要“边走边看”“边算边想”，否则容易铸成大错．

解： 当q=1时，因为S12=12a1,4S6=24a1，又因为S12=4S6，所以a1=0，舍去．

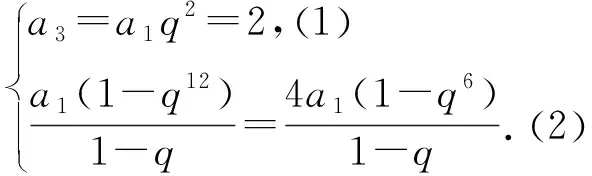
由(2)知，若q6≠1，则q6=3，

所以a9=a3q6=6．

若q6=1，则q=-1，所以a9=a3q6=2．

综上可知，a9的值为6或者2．

从阅卷反馈信息来看，本题难度系数约为0.06，得分极不理想，原因就在于学生想当然地认为：当q≠1时，q6≠1一定成立，所以a9=a3q6=6．丢掉了一个解，当q=-1时，a9=a3q6=2．这个案例告诫我们“边算边想”的必要性与合理性．

3.3 算后再想

算后再想是指对于一些解题思路多样化的数学问题，利用一种方法做出来之后，结合对问题更深层次的认知，还可以优化解题路径，给出更加完美的、富有智慧的解题方法，实现波利亚先生所倡导的“能不能一下子看出它来?”“能不能把这结果或方法用于其他问题? ”的境界．

案例3在锐角三角形ABC中，9tanAtanB+tanBtanC+tanCtanA的最小值为．

思路分析：本题条件非常弱化，只要求“锐角三角形”即可．观察目标函数不难发现：每一项都是两个正切值的乘积，其中角A与B关系对称．首先会想到利用“消元法”，消去tanC．

解法一：

所以9tanAtanB+tanBtanC+tanCtanA

不妨设tanA=a,tanB=b，

则9tanAtanB+tanBtanC+tanCtanA

这种方法从3元变为2元，再从2元变为1元，两次利用基本不等式求出最值，通过验证可知，等号可以取到．反思上述解题过程，笔者认为由于A与B是对称关系，因此最值肯定在A=B时取到，因此可以优化解题路径，给出如下解法．

解法二：根据对称性可知，当且仅当A=B时取到最值，此时C=π-2A，令tanA=a，

则9tanAtanB+tanBtanC+tanCtanA

余下同解法一．

另外，反思本题的条件，一是在锐角三角形ABC中，tanAtanBtanC=tanA+tanB+tanC恒成立；二是在目标函数9tanAtanB+tanBtanC+tanCtanA中，每一个式子都缺少第三项，因此可以对应相乘，实施“补美技巧”，从而一下子抓住了该问题的数学本质．

回顾本题解题方法的探索过程，笔者深有感慨，真可谓：涉浅水者见虾，其颇深者察鱼鳖，其尤甚者观蛟龙．

4 遵循“多想少算”的几条建议

4.1 树立以人为本理念，倡导智慧教育

在2017年版普通高中数学课程标准中，“课程的基本理念”浓缩为4条，分别从“学生发展为本”、“优化课程结构”“把握数学本质”“重视过程评价”四个关键点展开，这四个点恰好可以看成是一个三棱锥的四个顶点，以“优化课程结构”“把握数学本质”“重视过程评价”为底面上的三个顶点，共同“扛起”了“学生发展为本”这个顶点．由此可见，新课标旗帜鲜明地倡导“以人为本”教育理念，重视学生数学核心价值与学科素养的培养，亟待推进智慧教育．笔者认为，智慧教育的本质就是要重视过程，即审题的过程，谋划解题思路的过程，实施解题计划的过程，反思解题环节的过程．智慧教育就是要让学生积累基本数学活动的经验，会想问题，会做事情．因此数学解题教学中一定要把想的过程教给学生，让学生知道如何想解题思路？如何优化解题思路？如何反思解题思路？

4.2 提升解题教学境界，倡导深度教育．

章建跃先生曾批评当下解题教学的现状：搞“题型+技巧”，机械模仿多，独立思考少，数学思维层次不高．他提出数学解题教学的三重境界：知其然；知其所以然；何由以知其所以然．笔者认为，第一重境界是指教师最不该做的事情就是给学生一个绝妙的解法，形象地说“从帽子里变出一只兔子来”，而不知为什么，让学生感到自己无能，不是学数学的材料，打击其信心．第二重境界是指有些教师讲题不但讲怎么做，还能够讲清楚为什么要这样做，让学生感受到解题思路的合理性．但是你是怎么想到的呢？教师没有给出诠释．教师能够达到第二重境界已经很好了，但是还有提升空间．第三重境界是指有些老师讲题不但讲怎么做，还能够讲清楚为什么要这样做，并且深刻剖析解题思路的形成过程，介绍自己是怎么想的．第三重境界实际上是“授人以鱼，更授人以渔”．笔者认为，这重境界就是解题的深度教育，能够帮助学生学会独立思考，砥砺思维能力，提升思维品质，为“多想少算”打好坚实的基础．

4.3 做实数学解题过程，倡导精致教育．

精致教育是指精巧细致、精耕细作的教育．它是针对目前数学教育中“贪多求快”“粗放型”的现象提出来的，注重解题细节，追求尽善尽美，崇尚“小即是美”．笔者认为，解答数学问题就是要让学生扎扎实实地做题目，要精力集中、书写规范、思路清晰，逻辑性强，讲究速度与精度，会做的题目能够拿到满分，练好做题“童子功”．教师要给予学生充足的做数学的时间与空间，发挥学生的主观能动性，让学生亲历亲为，体验解题过程中的“酸甜苦辣”，积累成功的经验，也汲取失败的教训．解题精致教育大致包括三个环节：一是认真审读题目，广泛联想，初步拟定可能的几套解题方案；二是认真落实解题方案，边做边想，不断地优化调整解题思路，把题目做到底；三是解题后的反思与回顾，做后再想，不断缩减计算步骤，达到“想明白，说清楚，写简约”．