基于BP神经网络的旋风分离器分割粒径模化与预测

刘金鹏，赵兵涛，钱魏锋，李会梅

（1 上海理工大学能源与动力工程学院，上海200093；2 上海市动力工程多相流动与传热重点实验室，上海200093）

旋风分离器作为常用的离心式气固分离设备，广泛应用于固体粉尘收集、循环流化床、石油催化裂化、气溶胶采样等工业场景中[1-3]，其一般结构如图1所示。分割粒径（定义为旋风分离器分级效率为50%时的颗粒空气动力粒径）是评估旋风分离器分离性能的重要参数，小的分割粒径一般意味着高的分离性能[4]。

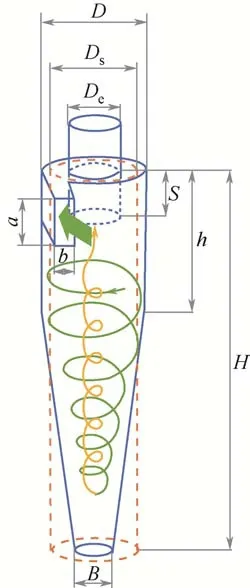
图1 旋风分离器结构尺寸

为预测分割粒径，基于多种模型和理论的表征方法在过去几十年相继被发展[5]。早期以理论模型[6-7]和半经验模型[8]为主，停留时间理论和平衡轨道理论的应用对分割粒径的表征有了详尽的物理描述。但由于近似简化和条件假设的建模方式，预测精度并不理想[9]。相较于对复杂机理的建模，基于数据驱动的多元回归模型受到关注[5]，它们主要将表征分割粒径大小的量纲为1 数Ψ0.5作为因变量，与操作参数[10]和部分尺寸参数[11]进行关联，模型决定系数可以达到0.980 以上，但没有考虑到其他重要尺寸参数的影响。Zhao等[9]模型间接关联了旋风分离器广义尺寸参数和操作参数，更全面地评估了分割粒径的影响因素，模型决定系数为0.973，但其预测精度仍有进一步提高的必要性。

近年来，人工神经网络凭借优越的非线性拟合能力在旋流分离领域得到重视[12]。如Safikhani 等[13]通过GMDH 型神经网络得到了分割粒径的预测模型，但只关联了部分尺寸参数。Elsayed 等[14]运用RBF神经网络对Stokes数预测，预测是基于训练集而不是测试集的结果且网络输入缺少重要操作参数的响应。因此关联全局的结构与操作参数、合理发展和选择自变量，比较与评估神经网络模型中的算法、参数及其优劣性，从而高精度模化旋风器的分离性能仍是当前面临的科学技术问题之一。

本研究的目的是通过关联旋风分离器全局尺寸参数和操作参数构建一个基于前馈性BP 神经网络（BPNN）的分割粒径预测模型，通过比较不同算法包括L-M算法[15]、拟牛顿算法[16]和贝叶斯正则化算法[17]以及隐含层神经元个数的组合预测性能对BPNN 模型进行优化，最后对BPNN 分割粒径模型的预测性能进行评价，并与其他理论模型、半经验模型和多元回归模型进行比较。本文以期为不同结构旋风分离器性能参数的评估提供一种精确有效的方法。

1 BPNN分割粒径模型模化过程

1.1 BP神经网络基本原理

BP 神经网络（back propagation neural network，BPNN）运用误差反向传播的方式修正权值、阈值[18]。由输入层、隐含层和输出层构成，隐含层神经元个数足够时，三层结构的BP 神经网络可以很好地逼近一个参数有限的不连续函数[19]。当有i 个输入、j 个隐含层神经元和k 个输出时，隐含层的输出如式(1)所示。

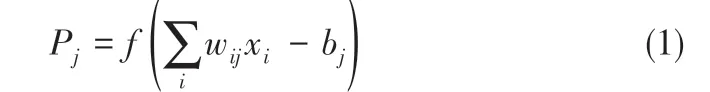
式中，wij为输入层与隐含层的连接权值；xi为输入变量；bj为隐含层阈值；f为隐含层激活函数。隐含层常用S型函数作为激活函数，主要分为logsigmoid 函数和tan-sigmoid 函数。虽然都存在着梯度消失的问题，但是相较于log-sigmoid函数，tansigmoid的输出是以0为中心的，收敛速度快，同时在非线性预测领域中得到了成功的应用[20]，所以本文选用tan-sigmoid 函数作为隐含层的激活函数，其表达式如式(2)所示。

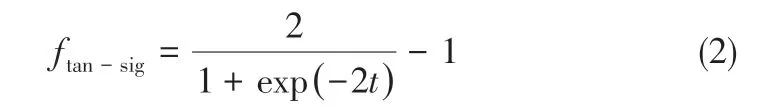
式中，t 为隐含层输入变量。输出层输出如式(3)所示。

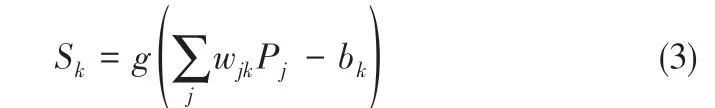
式中，wjk为隐含层与输出层的连接权值；bk为输出层阈值；g为输出层传递函数，本文选用线性函数purelin 函数作为输出层传递函数，其表达式如式(4)所示。

式中，a为输出层输入变量。

1.2 BP神经网络模型变量参数

旋风分离器主要包含8 个结构尺寸参数，如图1所示，分别是进口高度a、进口宽度b、排气芯管直径De、排气芯管插入深度S、筒体高度h、总高度H、排尘口直径B、筒体直径D，它们的改变对分割粒径有着不同程度的影响[21-25]。此外，Dring等[26]发现两个量纲为1 参数比(ρg/ρp)r0/Dp、Re0Dp/r0可用于描述旋流中粒子的轨迹，其中ρg为气体密度、ρp为颗粒密度、Dp为颗粒粒径、r0为初始旋流半径。从中可知颗粒粒径的量纲为1比Dp/r0与旋流雷诺数Re0高度关联，所以旋风分离器结构尺寸参数和操作参数对空气动力等效分割粒径dp0.5的综合影响表征如式(5)所示。

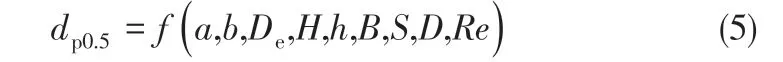
由于输入参数过多会使BP 神经网络模型的复杂度增加，所以需要降低数据维度来提高模型质量，另外对输入、输出参数的量纲为1处理可以进一步简化模型。

如图1 所示，在常见的筒锥结构旋风分离器中，筒段与锥段的直径不同导致颗粒的分离距离不同，Zhao等[9]为了克服这种不均匀性，运用等效体积法构建出等效分离距离Ds，其间接地关联了h、H、B、D 四个尺寸参数，运用Ds可以更综合地表征旋风分离器本体尺寸参数对分割粒径的影响，等效分离距离的量纲为1 几何参数可以表征如式(6)所示。

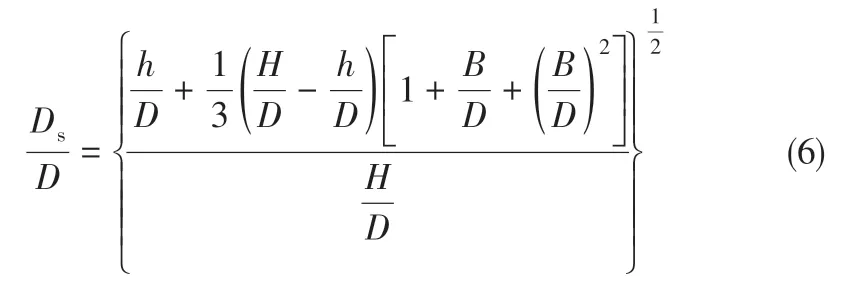
Moore等[10,27]的研究表明，流体流动特性对颗粒沉降的影响可以用气体雷诺数Re 表征，但是环形空间雷诺数Reann被认为对表征空气动力等效分割粒径大小的量纲为1数Ψ0.5有着更好的关联性，Reann、Ψ0.5计算分别如式(7)、式(8)所示。

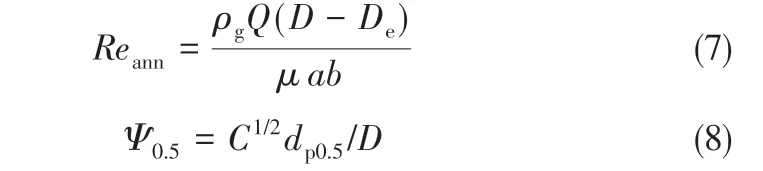
式中，Q为气体流量；C为Cunningham修正系数；Reann中包含着对外部尺寸参数进口高度a、进口宽度b、排气芯管直径De的间接表征。同时Lidén 等[11]认为Ψ0.5除了与Reann有很好的关联性外，S/D 对Ψ0.5也有着很大的影响。联合式(5)～式(8)，Ψ0.5与旋风分离器结构尺寸参数和操作参数之间的联系可以表征如式(9)所示。

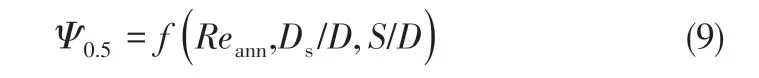
在神经网络建模中，选用Reann、Ds/D、S/D 三个量纲为1数作为BP神经网络的输入参数、Ψ0.5作为输出参数。

1.3 数据集划分与网络参数设置

本文使用156 组数据样本的数据集[28-39,8,24]建立BP 神经网络模型，表1 为数据集分布情况。通过分层抽样法按数据源属性划分，将数据分为14份，再运用Kennard-Stone 算法[40]将每份数据按照85%∶15%的比率划分为两份，合并每份中85%的样本作为训练集，15%的样本作为测试集。

在运用模型训练和测试时，均将参数归一化到[-1,1]区间内，最终模型输出的值经过反归一化转换成实际数量级的值。网络参数设置中迭代次数为1000次，目标精度为1×10-5，验证集最大失败次数为100次（贝叶斯正则化算法无此参数）。

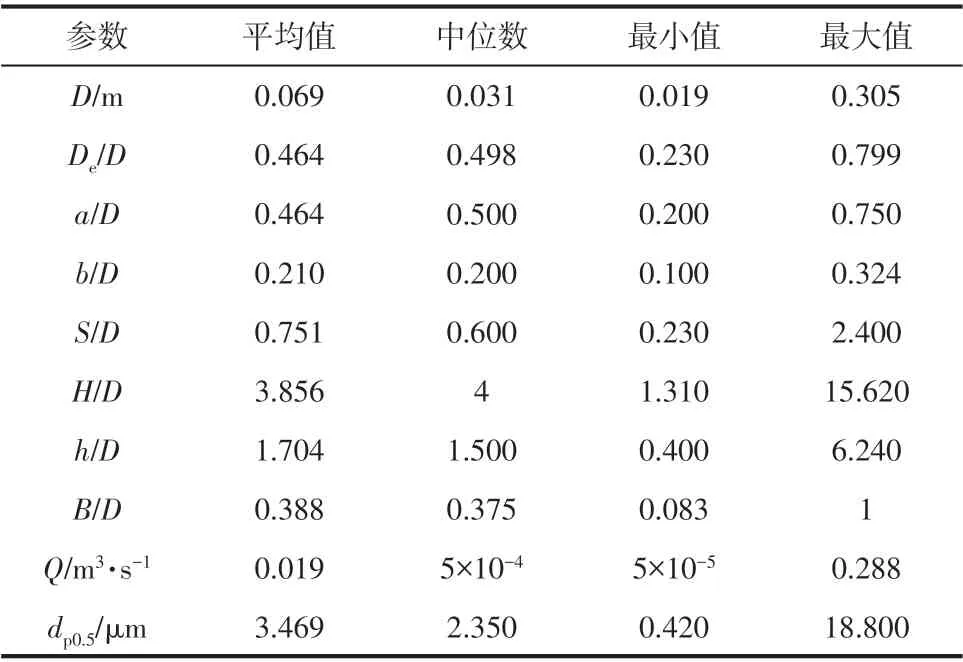
表1 数据集分布

1.4 评价指标

本文采用均方误差（E2）、决定系数（R2）作为评价指标，如式(10)、式(11)所示。

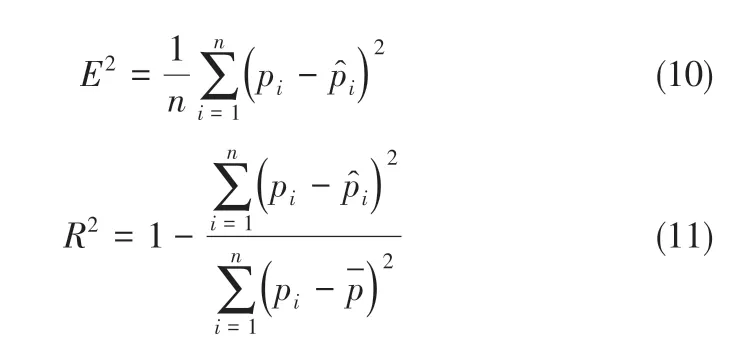
式中，n 为数据样本数；pi为实测值；为预测值；为实测数据平均值。

2 结果与讨论

2.1 神经元个数和训练算法的影响

为了对比不同神经元个数和训练算法对BP 神经网络预测性能的影响，选用L-M 算法、拟牛顿算法、贝叶斯正则化算法进行预测性能的比较，每个训练算法分别在隐含层神经元为6、7、8三个水平下对Ψ0.5进行预测。其中隐含层神经元个数为7的中间水平选取基于经验公式2m+1，m 为输入层神经元个数。为了避免网络初始权值、阈值随机性的影响，将每种组合的BP 神经网络连续运行10次，选取评价指标的10 次均值进行评估，对训练集和测试集预测的E2均值如图2所示。

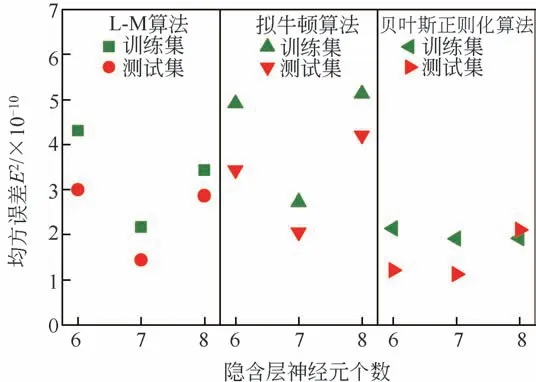
图2 不同BP神经网络模型E2比较

可以看到，在相同训练算法下，采用不同隐含层神经元个数对训练集和测试集的预测精度有影响。通过比较，在隐含层神经元个数为6、8时，各个训练算法的E2均大于神经元个数为7时的E2。因此7为最佳隐含层神经元个数，L-M算法、拟牛顿算法、贝叶斯正则化算法均取得较优的预测性能，对训练集预测的E2分别为2.175×10-10、2.725×10-10、1.919×10-10，对测试集预测的E2分别为1.446×10-10、2.064×10-10、1.121×10-10。

在隐含层神经元个数为7 时，从表2 中可以看到，3种训练算法对训练集和测试集预测的R2均大于0.95，表现出较好的预测能力。L-M算法对训练集和测试集预测的R2分别为0.965、0.977，预测精度高于拟牛顿算法，略低于贝叶斯正则化算法。其中贝叶斯正则化算法展现出了最优的预测性能，对训练集和测试集预测的R2分别为0.969、0.983。拥有自适应正则化参数的贝叶斯正则化算法能够更好地规避网络训练时欠拟合和过拟合的问题，进而保障BP 神经网络的鲁棒性和泛化性能，本文选择隐含层神经元个数为7 时基于贝叶斯正则化算法的BP 神经网络建立BR(Bayesian regularization)-BPNN分割粒径模型。

表2 不同训练函数10次预测R2的均值

2.2 BR-BPNN分割粒径模型性能

BPNN 初始权值、阈值的赋值具有随机性，会造成每一次运行最终迭代的权值、阈值不同。为了确定BP 神经网络的最优权值、阈值，应用BR-BPNN 分割粒径模型对训练集和测试集连续预测10次，对每次得到的E2进行比较。如图3所示，可以看出第9次对训练集和测试集预测得到的E2为10次中最小，分别为1.73×10-10、8.639×10-11。选用第9 次运行迭代出的权值、阈值作为BR-BPNN 分割粒径模型的权值、阈值，详细参数见表3，表中、、为输入层的3 个神经元与隐含层的j个神经元之间的权值；为输出层的1 个神经元与隐含层的j个神经元之间的权值；表示隐含层j个神经元的阈值；表示输出层1 个神经元的阈值。

图4 给出了BR-BPNN 分割粒径模型预测值与旋风分离器分割粒径实测值的比较。由图可知，对训练集和测试集中Ψ0.5的预测R2为0.972、0.987，BR-BPNN 分割粒径模型展现出较高的预测精度。其中对测试集预测的R2高于训练集，这表明经过训练集训练的神经网络成功地推广到测试集中，网络的可靠性得到了证实。同时数据维度的减少提高了BR-BPNN 分割粒径模型的质量，在训练过程中能够有效学习到数据特征，从而对新数据提供更好的预测能力。综上所述，此模型可以作为一种新的预测模型对旋风分离器分割粒径进行预测。

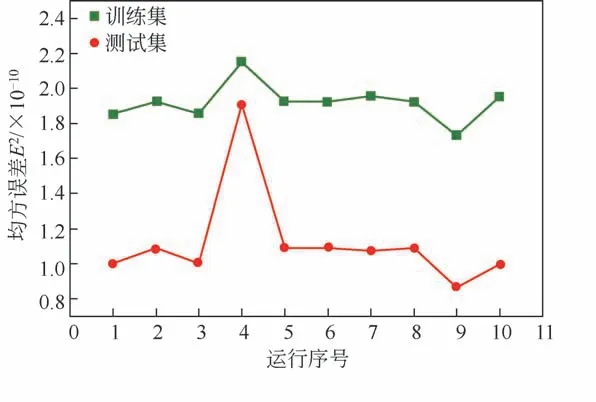
图3 BR-BPNN分割粒径模型10次预测E2对比

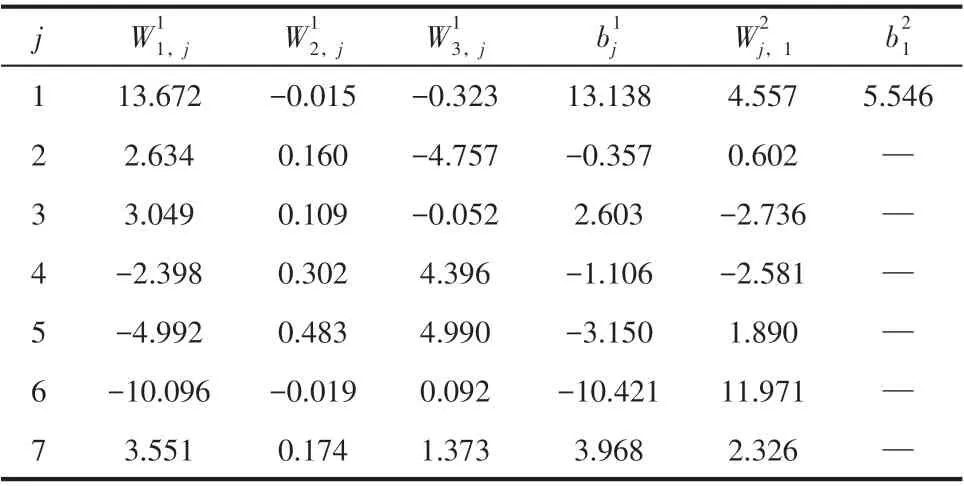
表3 BR-BPNN分割粒径模型权值阈值参数

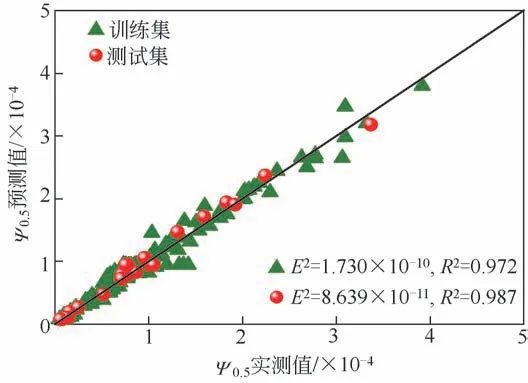
图4 BR-BPNN分割粒径模型预测值与实测值比较

2.3 不同分割粒径预测模型性能比较

表4 给出了BR-BPNN 分割粒径模型与其他分割粒径模型的性能比较，样本参数由本文测试集提供，预测结果统一换算为单位为μm 的dp0.5进行比较，其中多元回归模型的回归系数基于本文训练集重新获得。结果表明BR-BPNN 分割粒径模型拥有最小的E2和最大的R2分别为0.136、0.975，预测精度最高。Lapple模型[6]、Barth模型[7]和Iozia等模型[8]的预测产生了较大的E2，分别为2.131、2.079 和3.872。多元回归模型的预测精度较为相近，R2均大于0.94，略低于BR-BPNN分割粒径模型。

在理论模 型 中，Lapple 模型[6]和Barth 模型[7]对复杂机理的数学描述需要通过模型简化和假设实现。这会造成模型关键参数不易准确测得，如有效匝数、最大切向速度取值的偏差都会影响模型的预测性能。

表4 分割粒径预测模型性能比较

在半经验回归模型中，Iozia 等模型[8]作为对Barth模型[7]的改进，通过使用部分尺寸参数和操作参数与内外涡交界面的宽度和最大切向速度建立联系，并用实验数据进行回归得到系数。由于回归系数的实验数据仅来自筒体直径D为0.25m的11组旋风分离器参数，相对于本文测试集包含筒体直径范围为0.019～0.305m 的24 组旋风分离器的参数而言，模型泛化能力的局限性导致了较低的预测精度。

在多元回归模型中，Moore 等模型[27]取得了优于Lidén 等模型[11]的预测精度，R2为0.952。Lidén等模型[11]相较于Moore 等模型[27]关联了更多的尺寸数，但忽略了除S/D 之外的尺寸参数，使得S/D 在因变量中所占权重过大，导致预测精度不高。Zhao等模型[9]通过构建全局尺寸参数关联了所有结构尺寸参数和操作参数，在多元回归模型中展现出较好的预测性能，但由于BR-BPNN 分割粒径模型模化方式的先进性，相较于Zhao等模型[9]拥有更高的预测精度。

本文提出的BR-BPNN 分割粒径模型的输入参数不仅关联了与旋风分离器切割粒径有关的全部尺寸参数和操作参数，还将排气芯管插入深度的尺寸比S/D进行了单独关联，提高了排气芯管插入深度在因变量中的权重，以期对输出参数有更合理的响应，同时BP 神经网络又有着强大的非线性拟合能力，通过比较得出BR-BPNN 分割粒径模型的预测性能更有优势，对分割粒径预测的泛化性能更好。

3 结论

（1）为了精确预测分割粒径并更完全地表征其影响因素，在基于BR-BPNN 的分割粒径模型的输入参数中，环形空间雷诺数Reann耦合了操作参数Q和外部尺寸参数包括a、b 和De，基于等效体积法得到的等效分离距离量纲为1数Ds/D耦合了旋风分离器尺寸参数h/D、H/D、B/D，它们与S/D 一起反映了全部操作参数和结构尺寸参数对分割粒径的综合影响，可进一步对旋风分离器结构的优化设计提供参考。

（2）对BP神经网络运行10次的预测性能均值分析表明，训练算法和隐含层神经元个数对预测精度有影响。贝叶斯正则化算法作为训练算法时，其预测精度高于L-M 算法和拟牛顿算法，同时在隐含层神经元个数为7时达到了较优性能，运用此组合建立BR-BPNN 分割粒径模型对训练集预测的R2=0.972，对测试集预测的R2=0.987，展现出较优的预测能力，作为分割粒径的预测模型较为可靠。

（3）与已有的理论模型、半经验模型和多元回归模型比较，BR-BPNN 分割粒径模型具有较高的预测精度和较全面的尺寸参数和操作参数的响应能力。