基于灰色关联BP神经网络的压缩式蓄冷系统中的水合物生成量预测

杨文宇，谢应明，闫坤，邹俊华，舒胜

（上海理工大学能源与动力工程学院，上海200093）

CO2水合物作为一种新型蓄冷介质，具有蓄冷效率高、蓄冷密度大、传热效率高[1]、无毒[2]、环保及来源广泛等优点[3]，在蓄冷空调技术研究中得到国内外学者重视。作为蓄冷介质，水合物生成量对系统蓄冷量大小起决定作用。对于水合物的相平衡与生成量的预测研究，目前有经验、半经验模型和水合物理论预测模型可以对水合物的生成量进行预测。经验模型是利用实验中的实际数据拟合得到的模型，计算简单但精度不高，一般用于初步估算。理论模型是运用水合物生成时的动力学或热力学理论，通过试验得到的模型，预测误差小但对理论模型要求较高，理论模型一直都是研究的重点。王树立等[4]通过编程计算与实验研究对比发现，化学亲和力模型可准确预测复配体系水合物的生成。

近些年来，国内外学者利用诸如BP 神经网络模型、小波神经网络、马尔科夫链预测、灰色理论等模型[5-8]建立了不同的水合物预测模型。神经网络在水合物的研究中应用十分广泛，付康伟等[9]利用BP 神经网络算法建立陆域冻土地带的天然气水合物成藏模型，算法有效实用。马金凤等[10]根据地球化学数据建立水合物矿藏分类的神经网络模型，弥补了当前地球化学评价方法的部分缺点。Ghiasi等[11]通过利用最小二乘支持向量机及自适应模糊神经推理系统等模型对CO2水合物的生成条件进行了研究，取得了良好的预测结果。Mesbah等[12]利用多层感知机神经网络建立了不同TBAB 浓度下的CO2水合物相平衡压力模型，模型均方误差仅为0.0596。考虑到单一模型在使用时较为容易，但其自身存在不同的局限性，适用性也有所不同，所以使用组合模型的方式将不同的模型组合起来使用，进而提高预测精度[13-14]。组合模型的方式有很多，如利用遗传算法优化BP 神经网络的模型[15]及利用粒子群算法优化神经网络的模型等[16]。

CO2水合物生成的实验过程表明，CO2水合物可以在无添加剂或有添加剂的情况下生成，不同添加剂体系下的反应时间不同[17]。CO2水合物的生成量和反应时间受多种因素的影响，包括压力、初始温度、添加剂浓度及搅拌方式等[18-20]，传统的预测模型存在着计算复杂等缺点，因此建立一种适用性强的CO2水合物生成量预测模型是有必要的，可以解决预测CO2蓄冷系统水合物生成量的问题。

1 实验系统及数据处理

1.1 实验装置

实验装置如图1 所示，主要部件包括压缩机、水冷式气冷器、节流装置、CO2直接接触式反应釜、回热器和其他辅助设备，如干燥过滤器等。数据采集系统包括温度传感器（精度为±0.15℃）、压力传感器（精度为±0.1%）、气体质量流量计（精度为±0.1%）组成。系统数据采集由Agilent（安捷伦）系统完成。

图1 实验装置

1.2 数据处理

CO2水合反应方程如式(1)所示。

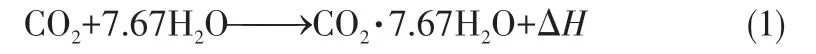
根据方程可以计算出水合反应所消耗水的质量mw,hyd，进而可以得到生成CO2水合物的质量，如式(2)所示。

1.3 实验方法与工况

为了研究系统中水合物的生成特性及系统变量对水合物生成量的影响，实验中设置3 个变量因素，分别为添加剂TBAB 浓度、CO2充注压力和初始温度。实验用水为自来水，由上海市自来水市北公司提供；实验用气为纯度99.99%的CO2，由上海市伟创标准气体分析技术有限公司提供；实验用添加剂为分析纯浓度级别的TBAB，由中国国药集团提供。具体的实验方法是：①将9L水加入反应釜；②整体抽真空；③开启反应釜处的恒温槽使水温达到要求的初始温度，并且打开数据采集装置；④充注CO2并达到指定压力；⑤启动压缩机，实时观察与记录反应情况，并在数据显示釜内下层温度下降至0℃时关闭压缩机等设备。实验工况见表1。

表1 实验工况

2 灰色关联BP 神经网络预测模型的建立

2.1 灰色关联预测模型基本介绍与构建

灰色模型是通过灰色量白化的方式，利用已知信息来预测未知信息的模型[21]。灰色关联预测模型［GRM(1,n)］是在灰色预测模型［GM(1,n)］的基础上，与灰色关联度的概念相结合的组合预测模型，其具有利用少量样本就可以得到精确结果的优点[22]。灰色模型中运用最多的模型是以时间为序列建立的GM模型，将无规律的原始数据进行一次累加生成，记为1-AGO，简称累加生成，生成有规律的新数列，然后将新数列曲线拟合。考虑到影响水合物生成量的因素众多，灰色模型的建立选用GM(1,n)模型，具体见式(3)～式(8)。

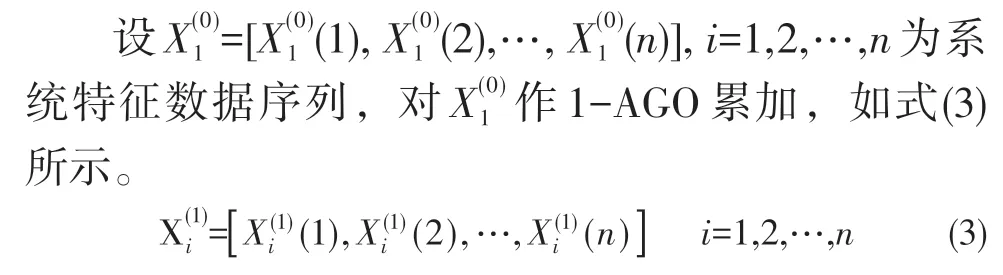
在GM(1,n)模型中，称a为发展系数，称bi为驱动系数，称a^ 为参数列。参数列a^ 满足式(4)。式(4)中，yN与B分别见式(5)、式(6)。

GM(1,n)模型的近似时间响应式见式(7)。

为了更好地分析不同影响因素对水合物生成量的影响度大小，需要进行灰色关联分析。灰色关联度的定义是：对于2个数据序列X1(0)和X2(0)，其灰色关联度如式(9)所示。

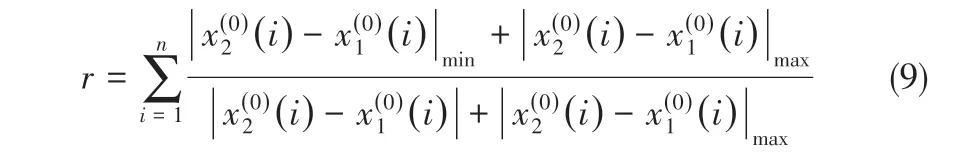
2.2 BP神经网络基本介绍与构建

BP 神经网络是在各领域中使用最普遍和有效的神经网络之一，属于前馈神经网络的一种[23-26]。BP 会得到广泛应用是因为其信号向前传递、误差反向传播的特点，在向前传递中，输入信号从输入层经隐含层逐层处理，直至输出层，若中间出现误差则输入到隐含层，以此类推，直到满足误差范围，这样使预测结果更加精准[27]。它的结构如图2所示。

图2 BP神经网络结构［28］

在构建BP神经网络前，需要将数据按照式(10)进行归一化处理，使处理后的数据均匀分布在0～1之间。

式中，Xnorm为归一化后的值；X为输入值；Xmax与Xmin分别为输入值里的最大值和最小值。

在将数据进行归一化处理后，将数据分为训练和测试两部分，利用Matlab 中的newff 函数构建BP神经网络。在模型得出结果后，需要将预测结果反归一化得出预测最终结果。根据算法原理，BP 神经网络的3个主要参数为传递函数、隐含层神经元个数和训练函数。传递函数选择tansig 函数，训练函数选择trainlm函数。

隐含层神经元个数可根据式(11)来确定大致范围。

式中，h 为隐含层神经元个数；ni为输入层神经元个数；no为输出层神经元个数；m为(1,10)范围内的常数。由式(11)可确定h的范围为3～12。为了更好地确定网络结构，在保持其他参数不变的情况下选取不同的隐含层节点数进行试算，结构如图3所示。

图3 不同隐含层节点数预测结果的平均相对误差

由图3 可知，当隐含层节点数为7 时平均相对误差最小，因此确定BP神经网络结构为3-7-1型，后续工作也基于此结构进行分析。

2.3 组合模型构建

2.4 影响因素的灰色关联度

根据灰色关联度的定义，求得3个影响因素与水合物生成量的灰色关联度，见表2。

表2 各影响因素与生成量的关联度

灰色关联度可以直观反映出两个因素变化趋势的相似程度，灰色关联度越大，相似程度越高。表格数据说明对水合物生成量影响最大的参数是充注压力，其次是初始温度与添加剂浓度。在实验中，充注压力的变化会直接改变参与水合反应的气体质量，对水合物生成量影响最直接，初始温度决定了反应的总体时长，而添加剂则是在前两者确定的基础上对水合物生成量的进一步提高，计算得出的关联度大小符合实际情况。

2.5 灰色关联预测模型预测结果

灰色预测方法具有可用少量数据得到较为精确的结果的优点，本文选取15组工况数据进行预测，结果如表3所示。

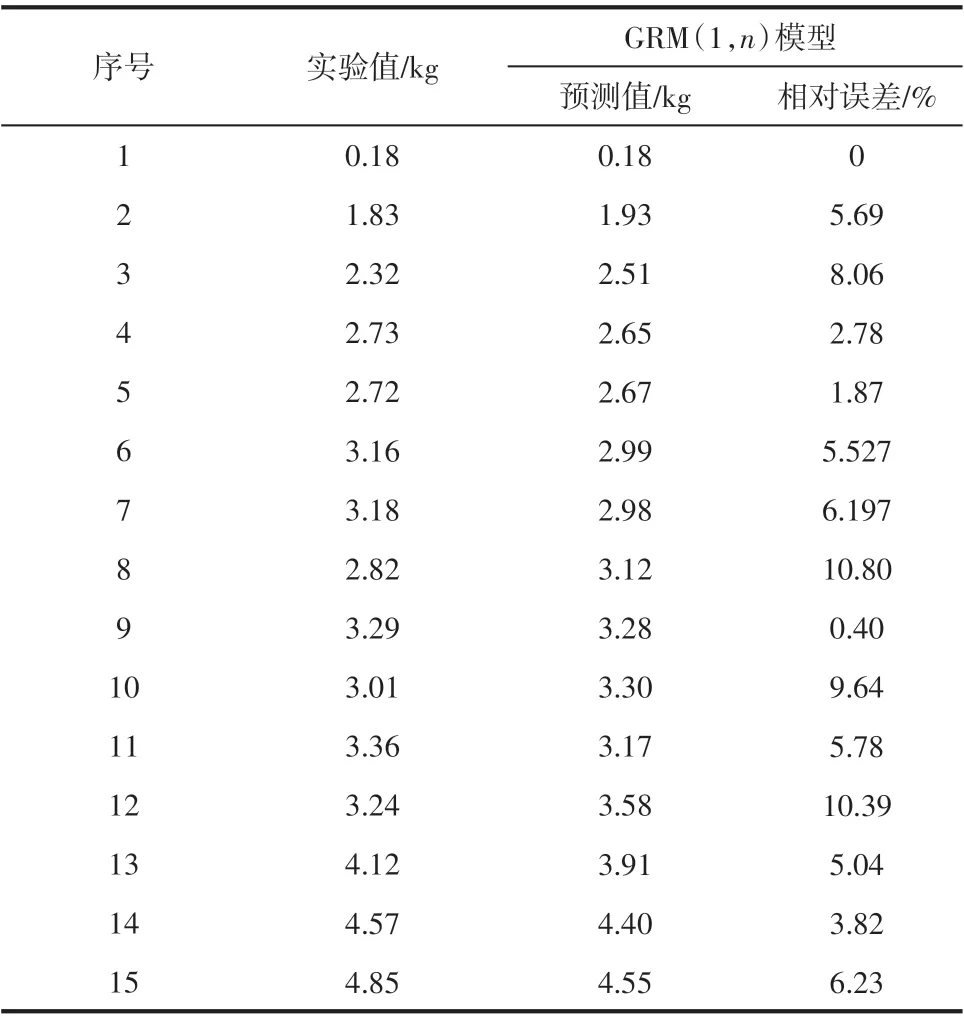
表3 灰色关联模型预测结果

首先对GRM(1,n)模型的预测值进行后验差检验：计算方差比c=S1/S2＝0.0353（其中S1、S2分别为原始序列和残差的均方差），并且小残差概率P=1，模拟值精度达到了一级标准，由此可知该模型可用于对系统水合物生成量预测。

2.6 BP神经网络预测结果

选取本文作者课题组累积的80 组数据作为训练数据，15 组数据为测试数据，通过确定网络的结构与参数进行训练，预测结果见表4。

分析两种单一模型结果可知，GRM(1, n)模型的平均相对误差5.48%小于BP 神经网络模型的5.79%，BP 神经网络模型的最大相对误差为13.52%，说明BP 神经网络在局部数据量较少的情况下精度较差，而GRM(1, n)模型对数据的需求量较少，最大相度误差也小于13.52%。然而GRM(1,n)模型在数据量过多时效果较差，所以为了充分利用单一模型的有效信息，克服单一模型的缺陷，引入组合预测模型。

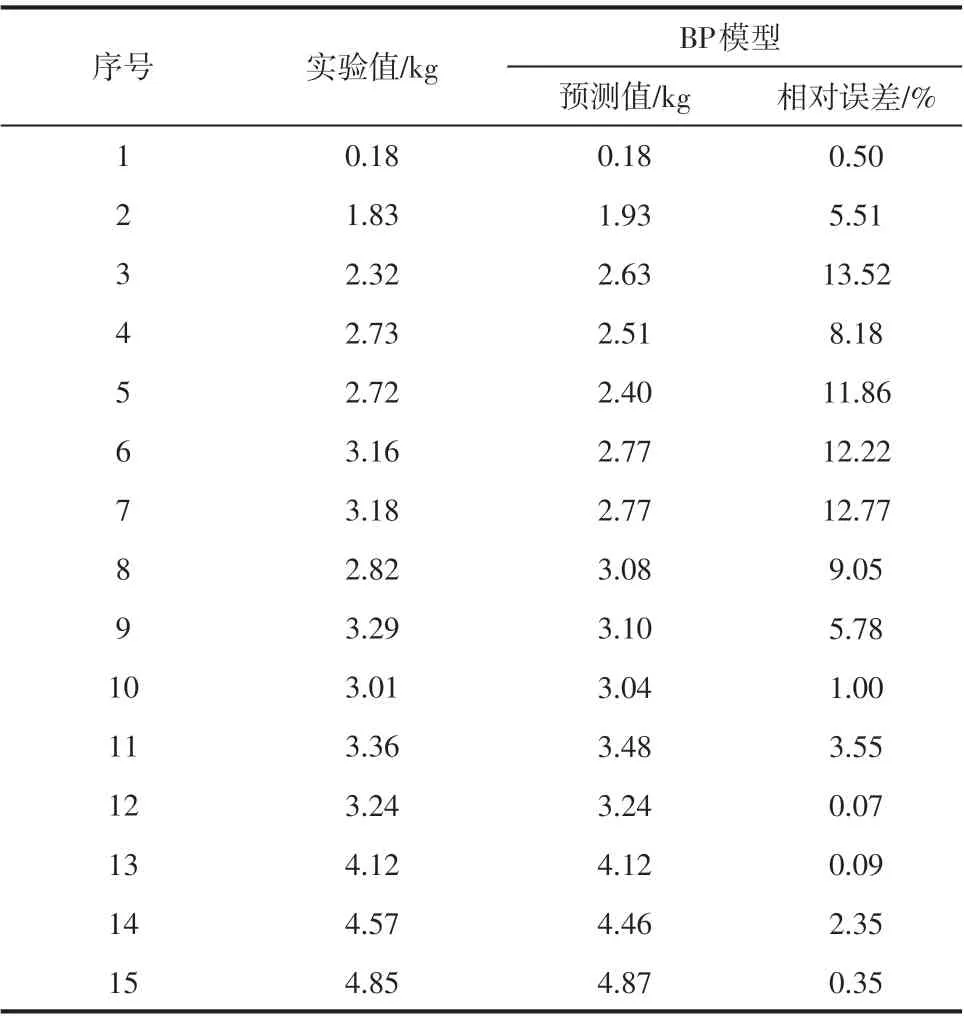
表4 BP神经网络模型预测结果

2.7 组合模型预测结果及比较

考虑到Matlab 程序编制简单实用，依然选择Matlab求解GRM(1,n)-BP神经网络组合模型，预测结果见表5。

从表3～表5 可以看出，组合模型具有较好的预测性，最大相对误差10.78%比其余两种模型小，平均相对误差5.36%，也优于单一模型。此外，GRM(1,n)模型、BP 神经网络模型及GRM(1,n)-BP组合模型的均方误差分别为0.0411、0.0470 及0.0329。均方误差可以评价数据的变化程度，其值越小，说明预测模型描述实验数据具有更好的精确度。GRM(1, n)-BP 组合模型的均方误差小于其余两种单一模型，进一步验证了组合模型预测结果更精确，且改善了个别预测误差较大数据的拟合值，能更好地用来预测压缩式系统CO2水合物的生成量。

2.8 组合模型验证

基于上述分析，为了进一步验证所建立的组合模型的适用性，利用GRM(1, n)-BP 神经网络组合模型对实验装置中的单一关键变量对水合物生成量的影响进行考察，基本思路为：使用标定的工况和操作方式，只改变添加剂TBAB 浓度、CO2充注压力和初始温度中的CO2充注压力这一关键变量，将工况代入组合模型，得到水合物生成量的预测值。

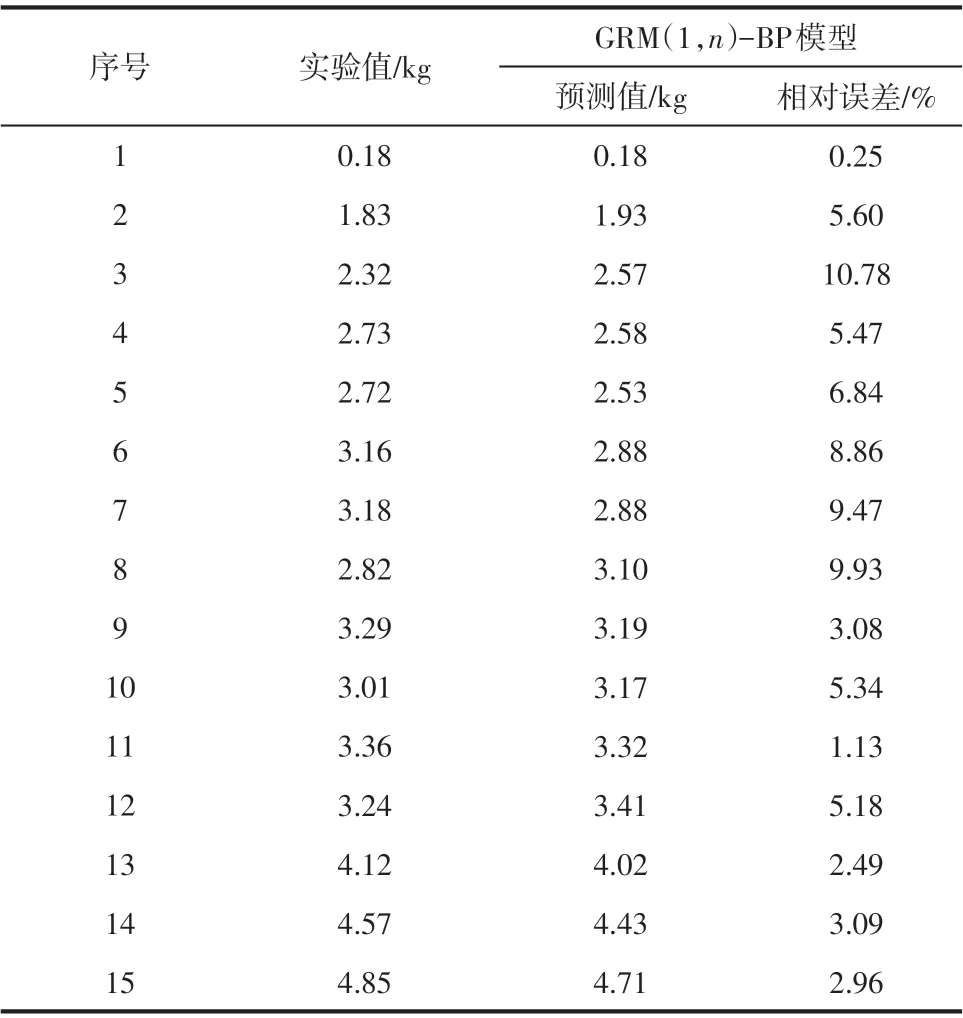
表5 组合模型预测结果

具体的工况：初始温度为298.15K，TBAB 质量分数为15%，充注压力为3.2～4.0MPa。将这一组工况代入GRM(1, n)-BP 神经网络组合模型，得到不同充注压力下的水合物生成量。结果如图4所示。

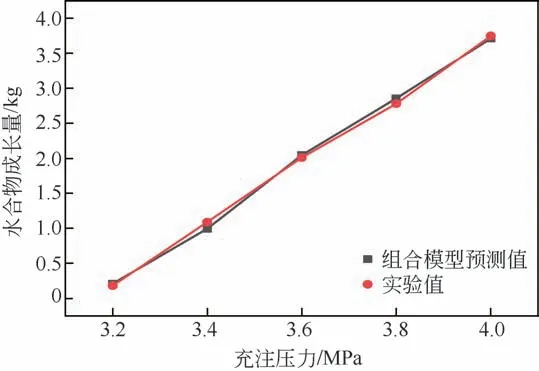
图4 充注压力对水合物生成量的影响

图4表示了充注压力对水合物生成量的影响情况，可见随着充注压力的增加，水合物生成量随之增加。这是由于CO2含量不同会造成气液间传质效果出现差异，从而对水合反应产生较大影响，同时，由于CO2在本实验中扮演着制冷剂的角色，其含量高低会造成制冷效果出现差异，从而影响系统的蓄冷总量和水合物生成量。结果表明，利用GRM(1, n)-BP 神经网络组合模型考察单一变量对水合物生成量的影响，其结果与实验值平均误差为6.56%，与反应机理也相符，进一步证明了预测模型的准确性。

3 结论

（1）基于实验系统的数据，选取充注压力、初始温度及添加剂浓度作为3个影响参数，通过利用灰色模型需求数据量少、准确度高的优点建立GRM(1, n)-BP 神经网络组合模型，对实验系统中CO2水合物生成量进行了模拟，并对比分析了GRM(1,n)模型、BP 神经网络模型及GRM(1,n)-BP神经网络组合模型的预测误差。

（2）仿真结果表明，GRM(1, n)-BP 神经网络组合模型能够较为准确地预测实验系统的水合物生成量，预测的平均相对误差为5.36%，均方误差为0.0329，与单一模型相比具有更好的预测性能。

（3）应用建立的GRM(1, n)-BP 神经网络组合模型考察了充注压力对水合物生成量的影响，预测值与趋势均符合实验机理，进一步说明了所建模型的准确性。

（4）由于影响水合物生成的因素较多，在数据量更充足的情况下，模型能够拥有更好的预测精度，使应用范围更加宽广。