城市快速路交织区运行风险预测模型
许 甜, 苏东兰, 赵 明, 王 晶
(1.中交第一公路勘察设计研究院有限公司, 西安 710065; 2.苏州科技大学土木工程学院, 江苏省生态道路技术产业化工程研究中心, 苏州 215011; 3.广东省路桥建设发展有限公司, 广州 510623; 4.同济大学道路与交通工程教育部重点试验室, 上海 201804)
城市快速路系统是由基本路段、立交、进出口、辅道及其连接点等组合而成的。随着城市快速路系统发展、路网加密,城市快速路与地面道路相交增加,在立交区域和进出口路段等不可避免地出现了很多复杂的交织区。交织区汇集了不同方向与不同类型的车流,多股交通流在较短路段内交织使得该区域产生大量的车辆换道行为,造成交织区交通冲突数量增多,从而导致交织区内交通安全水平降低。
20世纪50年代,美国最早开始了有关城市快速路通行效率的研究,编制了道路通行能力手册,提出了交织区具体的设计方案与安全标准[1]。直至2000年,道路通行能力手册HCM2000中,依据交织车流数量对交织区进行类型划分,通过计算交织区结构、交织比、长度以及交通量等参数得出交织区通行能力。此后,Lertworawanich等[2]利用间隙可接受理论细化车辆变道行为对不同几何构型的交织区建立了道路通行能力模型。Heikoop等[3]采用微观仿真软件FOSIM对交织区交通运行状态进行模拟;Diamandouro等[4]研究表明夜晚雨天情况下,交织区路面标线可见度对不同年龄及性别人群驾驶行为的影响。中国关于交织区的研究在方法上借鉴了HCM2000的计算方法,划分了交织区服务等级。研究初期,徐吉谦[5]、任福田等[6]对环形交叉口通行能力进行了分析,建立了相应的交织区交通流模型。近年来,中国学者在交织区、分合流区等瓶颈区域交通特性方面展开了大量研究。陈宽民等[7]探明了匝道出入口、合流区、分流区的车辆运行速度与交通量之间的相互关系;冯玉荣等[8]提出了通行能力的改进模型,该模型适用面更广、准确性更高;冯星宇[9]以负荷度作为主要指标、密度作为次要指标,研究提出了更为细化的交织区服务水平划分标准;陈亮等[10]考虑临时驶出车辆的影响,结合车辆变道安全间距、变道决策等因素,建立了基于元胞自动机的多车道交织区离散模型,基于此探明了交织区拥堵形成机制;安旭等[11]建立了针对交织区的元胞自动机模型,对比分析了交织区是否设置隔离带的两种车道分配情况下交织区及非交织区分别进行了数值的模拟和分析,并提出了隔离带设置方法。
可见,目前中外学者的研究主要的内容涵盖了快速路交织区通行能力、服务水平、驾驶行为、安全控制等方面,部分学者还研究了出入口间距、匝道类型对通行效率与行车安全的影响[12-14]。然而,对于快速路交织区运行风险预测与量化评价方面的研究较少。据此,在中外已有技术现状调研的基础上,针对城市快速路交织区运行风险预测模型开展研究。首先采用交织区断面线圈数据及自然驾驶行驶速度数据,分析城市快速路交织区运行特点,然后采用VISSIM交通仿真方法分析交织区道路几何线形、交通流、驾驶行为等因素对交织区运行安全状况的影响,建立快速路交织区运行风险预测模型,提出风险分级标准,最后采用无人机航拍交通量数据对预测模型误差进行分析,以期为城市快速路交织区的风险预测与评估提供参考。
1 交织区交通运行特点分析
1.1 断面交通流量
对上海市内环线天钥桥路-曹溪立交、延安高架北线江苏路-凯旋路交织区完整两周的线圈检测数据进行调研和统计分析。计算两个交织区内每条车道流量占总流量的比值,并将计算结果列于表1中。分析表1可以看出,交织区交通量由内侧车道向外侧车道逐渐减小。
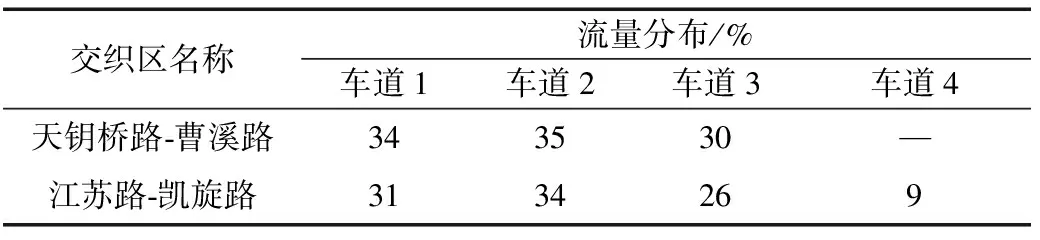
表1 交织区车道流量分布
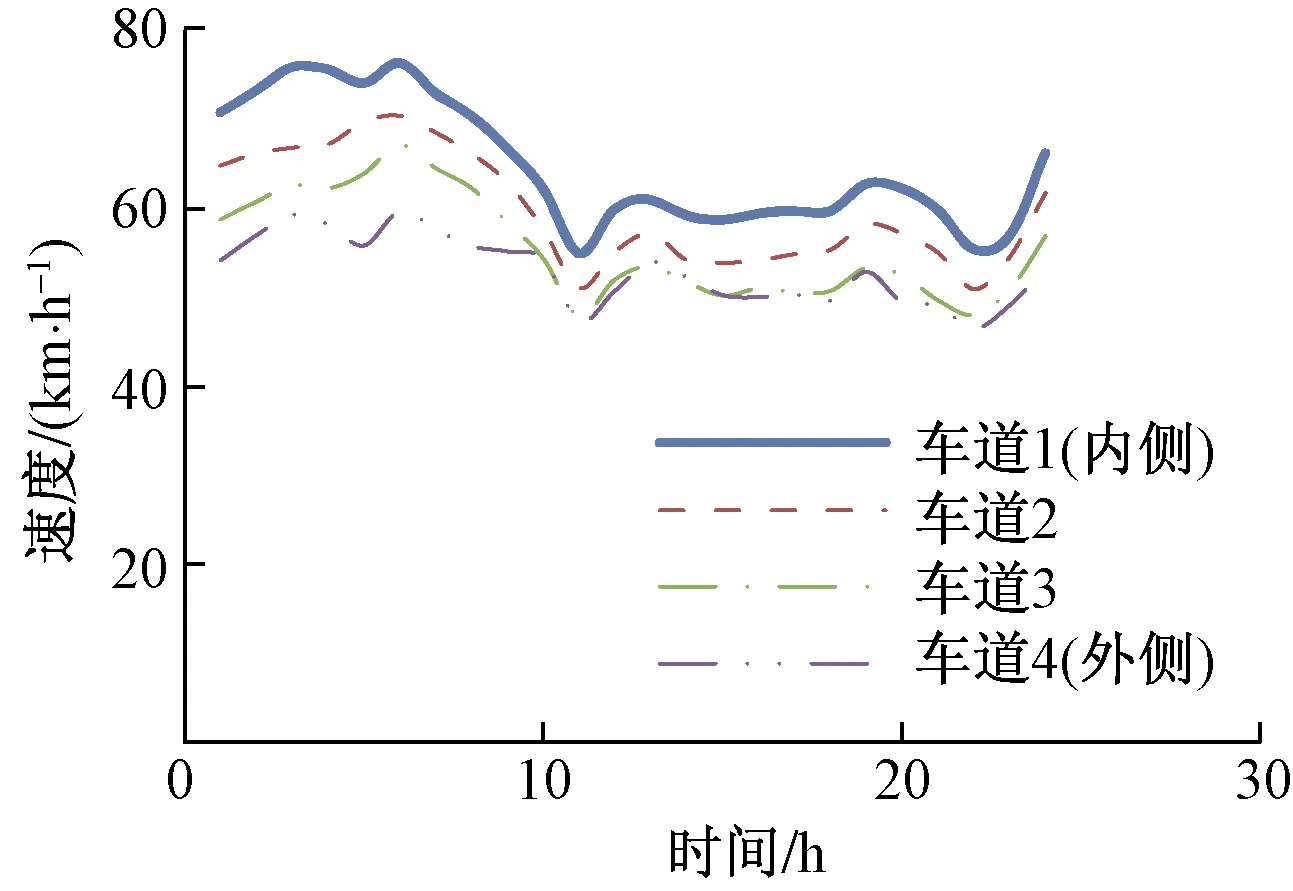
图1 江苏路-凯旋路交织区车速统计Fig.1 Speed statistics of Jiangsu Road to Kaixuan Road
将江苏路-凯旋路交织区不同车道不同时间车流平均车速统计结果绘制于图1中。由图1可知,交织区车流的平均速度由内侧车道向外侧车道逐渐减小。
综上可知,交织区路段由于发生分合流等变道,外侧车道交通量低于内侧和中间车道,比例也相对稳定;中间和内侧车道车流受到其他车辆换道干扰较小,因此车流平均速度高于外侧车道。
1.2 单车行驶速度
利用数据采集车通过自然驾驶的方式采集单车交通运行状况数据,采集数据包括速度与加速度,数据采集频率为2 Hz,可采集的车辆速度精度为0.2 km/h,采集车外观如图2所示。采集路段为延安高架江苏路-凯旋路交织区,交织区长度为 297 m,共有4 条行车道。
数据采集车行驶路径包括两条:主线-出口匝道(上游180 m影响区-交织区-出口匝道)、入口匝道-主线(入口匝道-交织区-下游180 m影响区)。同一路径采集车行驶3 次,对采集的车辆速度和加速度进行统计计算,获得各区间路段的平均车速和平均加速度绝对值。计算结果如表2所示。

图2 移动数据采集车外观Fig.2 Mobile data acquisition vehicle

表2 平均车速和加速度分布
分析表2可以看出,两种行驶路径下车辆在交织段的平均车速均远低于其他路段,且加速度绝对值高于其他路段。分析这一现象产生的原因是:采集车在交织区行驶时,周围车辆为保持行驶目的进行换道,产生的交织行为对采集车干扰较大,导致车辆平均车速总体偏低。
综上可知,交织区内车辆的分合流等变道行为使得该区域内车辆行驶速度、通行效率下降,车辆的加减速绝对值增大,这一现象增加了交织区交通运行发生紊乱的风险。
2 交织区交通运行风险预测模型
2.1 预测指标
目前,对普通路段、平面交叉口、交织区等路段进行风险分析时,常常使用的指标为交通冲突数(traffic conflict, AC)或交通冲突数与混合交通当量(mixed passenger car unit, MPCU)的比值。与平面交叉口相似,交织区内交通量是交通冲突数的重要影响因素,交通量越大,交织区内产生交通冲突的概率就越大,交通冲突数也就越多;由于城市快速路交织区长度有限,车辆须在一定的长度范围内完成变道行为,因此交通冲突数还与交织区长度具有紧密关系。
基于以上分析,以交织区内交通冲突数与交通量、交织区长度的比值,即车公里冲突率(average traffic conflict,ATC)作为交织区运行风险的预测指标,其计算方法为
ATC=TC/(QL)
(1)
式(1)中:ATC为车公里冲突率,次/(veh/h·km);TC为时均冲突次数;Q为在一定交通条件下单位时间内通过交织区某一断面的车辆数,veh/h;L为交织区长度,km。
2.2 VISSIM交通仿真
由于既有环形线圈埋设间距大、路侧宽度有限,路侧交通调查可行性低、浮动车数据样本量少、视频监测数据提取工作量大等现实原因,城市快速路交织区实际交通运行数据获取难度大。因此,采用VISSIM交通仿真模拟典型交织区的交通流状况,为交织区运行风险预测模型建立提供基础数据。
2.2.1 参数标定
实地交通状况调研与文献研究发现,交织区几何线形与交通流状况是影响路段通行效率与行车安全性的重要因素。据此,选定的仿真参数分别为交织区长度、交织区车道数、交通量、交织流量比与汇出比。为探究各影响因素对交通冲突的影响,进行VISSIM交通仿真计算,各参数变量范围标定依据如下。
(1)交织区长度L。参考HCM2010将交织区的交织长度限定在0.75 km范围内,试验中交织区长度标定为0.15~0.75 km,步长取0.15 km。
(2)交织区车道数n。根据上海快速路交织区实际调研发现,交织区内车道数往往为3 车道及以上,最多不超过6 车道。标定仿真试验交织区车道数分别为3、4、5、6。
(3)交通量Q。根据对上海市快速路线圈数据一天内交织区交通量变化统计结果,标定仿真交通量为1 000~5 000 veh/h,步长取1 000 veh/h。
(4)交织流量比VR。根据上海市20 个交织区的实际交织流量比计算结果[18],标定交织区流量比为0.2~0.6,步长取0.1。
(5)汇出比r。根据对上海市快速路线圈数据,汇出比标定为0.1~0.5,步长取0.1。
2.2.2 仿真试验
由于交通仿真试验共选取了5个基本变量,每个变量有4~5个水平,存在4×54=2 500种组合,考虑到完全试验工作量巨大,采用正交设计表L25(56)进行VISSIM仿真试验设计。在VISSIM仿真中完成上述25 组试验,得到每组试验的交通冲突次数并计算出车公里冲突率ATC,结果如表3所示。

表3 车公里冲突率计算结果
2.3 预测模型构建
基于交通仿真结果,分析交织区长度、交织区车道数、交通量、交织流量比和汇出比与交织区车公里冲突的相关关系,对比线性、指数、对数与多项式这几种拟合结果后,选择多项式非线性公式进行拟合,结果如图3所示。
由图3可见,ATC与交织区长度负相关,与交织流量比、车道数、汇出比、交通量均为正相关。进一步量化因素耦合后对交织区运行风险的影响,采用多元非线性回归分析方程拟合得到的预测指标计算公式为
ATC=a1f1(L)+a2f2(n)+a3f3(Q)+
a4f4(VR)+a5f5(r)+C
(2)
式(2)中:L为交织区长度,km;n为交织区车道数;Q为交织区交通量,veh/h;VR为交织流量比;r为汇出比。f1、f2、f3、f4、f5为各个因素与ATC的影响关系,即单因素方程;a1、a2、a3、a4、a5为相关系数;C为常数项。
利用VISSIM交通仿真结果进行回归拟合,获得该多元非线性回归分析计算方程相关系数、单因素方程及常数项。a1、a2、a3、a4、a5分别为0.964、-0.246、1.101、0.986、1.043;常数项C=-8.254。单因素方程为

图3 不同变量参数与ATC的关系Fig.3 Relationship between variable parameters and vehicle-kilometer conflict
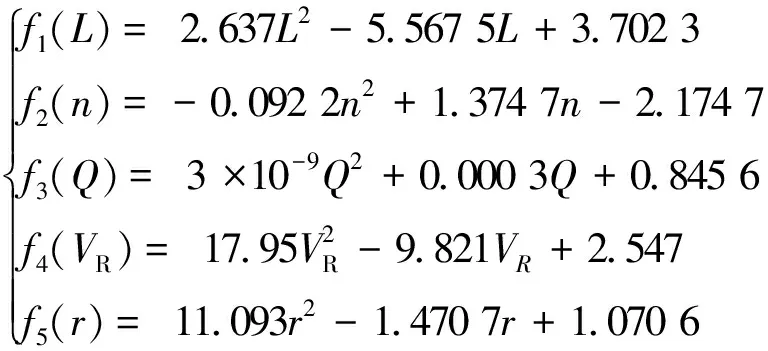
(3)
相关系数及常数项为:a1=0.964,a2=-0.246,a3=1.101,a4=0.986,a5=1.043,C=-8.254。
最终形成交织区交通运行风险预测模型为
ATC=(0.964,-0.246,1.101,0.986,1.043)×
8.254=-2.542L2-0.023N2+3.3×
5.367L-0.338N+0.000 3Q-
9.684VR-1.534r-6.729
(4)
2.4 风险等级划分
由于交通事故数据采集难度较大,未获得与交通仿真标定参数相对应的交织区交通事故资料,且目前快速路交织区运行风险暂无普遍认可的评价标准可循。因此,通过对不同参数交织区的仿真得到若干组指标值,借助聚类分析的方法对ATC数值进行迭代分析,得到其聚类中心,作为交织区运行风险分析的标准依据。
据此,采用K均值聚类进行聚类分析,并运行风险等级划分,将交织区的运行风险水平分为低风险、中等风险和高风险3类,即K=3。选用SPSS软件对25组不同组合条件下得到的ATC进行迭代聚类,获得3个聚类中心值,分别为0.58、2.72、4.76,对应风险等级为低风险、中等风险、高风险。据此对不同条件下交通仿真得到的ATC值进行分类:低风险时,ATC取值范围为0.100~1.890;中等风险时,ATC取值范围为2.200~3.568;高风险时,ATC取值范围为4.020~5.144。建立快速路交织区交通运行风险分级如表4所示。
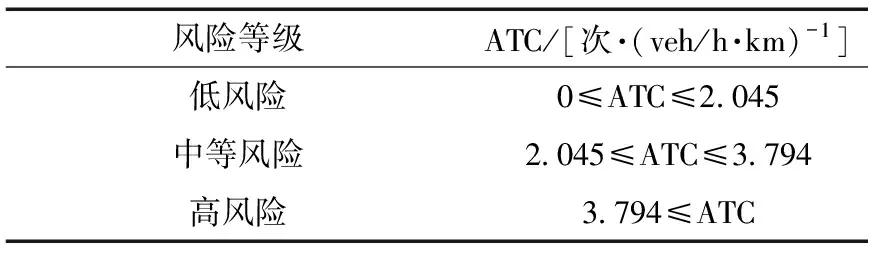
表4 城市快速路交织区交通运行风险分级标准
3 预测模型误差分析
3.1 交通数据采集
采用大疆PHANTOMB 3 ADVANCED无人机拍摄上海南北高架东线北京西路-威海路交织区交通流,该交织区长度为150 m,示意图如图4所示。
对拍摄到的交织区交通流运行视频进行统计分析,计算得到总交通流量Q=3 765 veh/h,交通流量比VR=0.269,汇出比r=0.499。

图4 北京西路-威海路交织区示意图Fig.4 Schematic diagram of Beijing west road-Weihai road weaving area
3.2 模型预测误差分析
按交织区长度、车道数构建VISSIM仿真场景,输入各车道实际交通量进行仿真,采集得到单位时间内交通仿真冲突次数,按照式(1)计算得到ATC=4.417。同时,利用式(4)计算出预测ATC=4.834,进一步计算得到预测值的误差为9.45%。可见,所建立预测模型的误差较小,在可接受范围内。这在一定程度上说明了采用构建模型的方法对城市快速路交织区的运行风险进行预测和评价是可行的。
采用预测模型的方式可以快速地量化分析城市快速路交织区的运行风险,以供城市快速路管理和设计人员参考,有助于提升城市快速路交通区运行安全性。本研究旨在给出城市快速路交织区运行风险预测模型的构建方法,并探讨其可行性。后续将进一步开展相关试验研究,以精确化预测模型的参数,并对预测模型的可靠性进行验证。
4 结语
在中外已有技术现状调研的基础上,采用线圈数据搜集、VISSIM仿真试验、无人机数据采集等手段,针对城市快速路交织区运行风险预测模型开展研究,得到主要结论如下。
(1)基于交织区车道断面线圈数据及自然驾驶试验采集数据分析了快速路交织区运行特性,结果表明,交织区内车辆的分合流等变道行为使得该区域内车辆行驶速度、通行效率下降,车辆的加减速绝对值增大。
(2)探讨提出了较之于运行风险预测指标ATC,基于VISSIM仿真试验,分析了交织区运行风险影响因素,并建立了运行风险预测模型,同时通过K均值聚类进行聚类分析,继而提出了运行风险分级标准。
(3)通过无人机采集实际交织区交通数据对所建立预测模型进行误差分析,结果表明,采用构建预测模型的方法对运行风险进行预测是可行的,该模型可用以量化分析交织区运行风险。
(4)需进一步开展的研究包括城市快速路交织区运行风险预测模型参数试验研究、预测模型的有效性和可靠性验证。

