基于深度学习的二维航空大地电磁数据反演
李 赓, 曹飞翔
(河南理工大学物理与电子信息学院, 焦作 454150)
大地电磁测深法是一种天然源频率域电磁法,其以自然产生的平面电磁波为场源,通过观测地表正交的电磁场分量获取地下的电阻率结构[1]。然而,在地形较为复杂的地区,地面大地电磁法施工效率较低,大面积勘探成本急剧上升。目前,航空大地电磁法具有机动灵活、成本低、效率高的优点,能够在复杂环境中进行大规模快速勘探,已被应用于油气勘探、矿产资源勘探等领域[2-4]。
航空大地电磁法利用高空中电离层产生的平面波作为发射源,通过搭载在直升机上的探测设备采集垂直磁场信号,同时在地面基站采集水平磁场信号,获得倾子数据。经反演[5-6]计算,得到地下介质的电性结构。许智博等[7]采用非线性共轭梯度算法实现了二维航空大地电磁反演计算,大大加快了目标函数的收敛速度。苏扬等[8]针对层状介质模型推导实现了广义模型约束条件下时间域航空电磁一维反演。殷长春等[9]通过引入双向约束实现了航空电磁拟空间约束反演。
目前的电磁数据反演算法基本都是基于吉洪诺夫正则化的反演算法,这类方法的主要工作是求解目标函数的偏导数,偏导数的求解以牛顿法的变种(求解梯度向量、海森矩阵)为主,这会导致反演结果对反演初始模型依赖高,且易陷入局部极小值。针对传统电磁反演方法存在的问题,通过引入智能非线性算法来解决电磁反演问题,已被证明有效可行。陈紫静[10]采用粒子群算法顺利完成了大地电磁测深资料反演。王鹤等[11]实现了基于遗传神经网络的大地电磁数据反演。李栋[12]采用人工神经网络开展了航空瞬变电磁拟电阻率反演成像研究工作。邸龙[13]采用人工蜂群算法对不同类型的地质开展了大地电磁非线性反演方法的研究。
现基于二维航空大地电磁法正演理论基础,首先,针对地下介质中嵌入异常体的地电模型,采用有限元方法计算其倾子数据,并结合地下电阻率值标签,构建深度学习样本数据集。接着采用深度学习卷积神经网络进行二维航空大地电磁倾子数据反演,针对不同埋深的异常体地电模型,分别采用传统电磁反演和深度学习反演方法开展二维航空电磁数据反演研究。
1 二维航空大地电磁正演理论
1.1 边值问题
研究的直升机航空大地电磁法是频率域电磁方法,满足频率域麦克斯韦方程组,其表达形式为
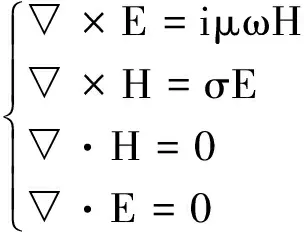
(1)
式(1)中:μ为介质磁导率;ω为角频率,rad/s;σ=1/ρ,S/m,表示介质电导率;E为电场强度;H为磁场矢量;表示哈密顿运算符。
在二维地电模型中,磁场的垂直分量Hz只存在于TE模式中。因此,二维航空大地电磁法控制方程为
(2)
式(2)中:Ex为电场E在x轴方向上的分量。
式(2)可进一步表示为
(3)
式(3)中:u=Ex;τ表示自由电荷密度,C/m3;τ=1/iωμ;λ表示电导率,S/m,λ=σ。
为了求解式(3),还必须给出边界条件。现假设求解区域如图1所示,研究对象为天然电磁场,场源在距离地面足够远的高空中,电磁场以平面波的形式垂直入射地下介质。
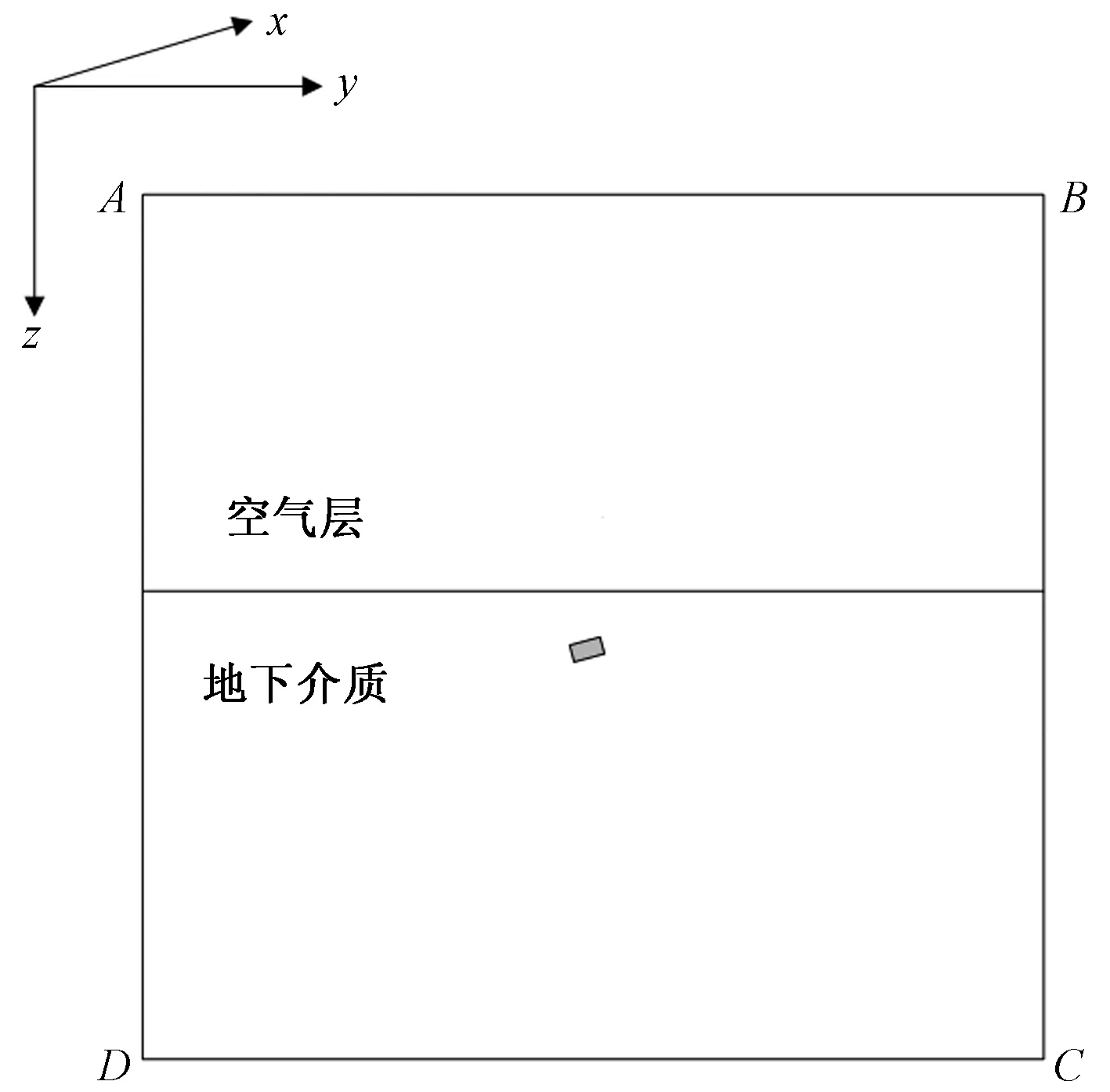
图1 TE模式求解区域Fig.1 Solution domain for TE polarization
TE模式下的边界条件如下。
(1)上边界AB离地面足够远,使异常场值在AB上为0,该处u=1。
(2)下边界CD以下为均匀介质,其边界条件为u/n+ku=0。其中:n表示外法线;k为复波数,为CD以下介质的电导率。
(3)左右边界AD、BC处的边界条件为u/n=0。
综上所述,边值问题可总结为
(4)
式(4)中:Ω表示求解区域;AB、CD、AD、BC分别表示求解区域的上、下、左、右边界。
1.2 有限元求解方法
与上述边值问题等价的变分问题为
(5)
式(5)中:Ω为待求解区域面积;Г为Ω边界。
有限单元法在求解上述变分问题时,首先将待求解区域离散为一系列互不重合的四边形单元;然后在各离散单元内用插值函数与单元中节点上未知电场值的乘积作为近似解,将近似解代入边值问题后,在每个单元上可得一个复系数线性方程组。向该复系数线性方程组中加入求解边界条件(定解条件),假设为u=b。最终可得到一个大型稀疏对称复系数线性方程组,该大型稀疏对称复稀疏线性方程组表示为
(6)
式(6)中:Ke和ue分别表示单元系数矩阵和向量;Ne表示单元总个数。采用直接求解法求解该方程组即可得到求解区域内各节点电场值组成的向量u。
1.3 倾子响应计算公式
研究的二维航空大地电磁数据为倾子数据。当地下介质电阻率在水平方向上发生变化时,磁场的垂直分量Hz≠0,此时,Hz与Hx和Hy之间的复系数关系为
(7)
式(7)中:T=[Tzx,Tzy]称为倾子。
TE模式下式(7)可进一步表示为
Hz=TzyHy
(8)
最终二维倾子响应计算公式为
(9)
2 传统电磁反演与深度学习反演理论
2.1 传统电磁反演
利用传统电磁反演方法进行反演时,首先构建出带有约束项的观测数据目标函数,接着采用反演算法求解该目标函数梯度的极小值,最终获得最优的反演地电模型。传统电磁反演方法将带有约束项的观测数据目标函数定义为
Φ(m)=[d-F(m)]TV-1[d-F(m)]+
λmTLTLm
(10)
式(10)中:d=[d1,d2,…,dN]为N维倾子数据向量;m=[m1,m2,…,mM]为M维模型参数向量;F(·)表示从模型向量到倾子数据向量映射的正演算子;V为一个用来描述观测数据误差的正定矩阵;λ为正则化因子;L表示二阶差分矩阵。
传统电磁反演方法的最终目标就是采用合适的反演算法求解上述目标函数梯度的极小值。现采用非线性性共轭梯度(nonlinear conjugate gradients, NLCG)反演算法求解目标函数梯度的极小值。利用目标函数的梯度信息对模型向量进行修正,从而实现搜索目标函数极小值的迭代过程。
NLCG算法通过初始化反演模型m=m0,设置最大迭代次数为I,在每次迭代时,计算目标函数、梯度,从而计算出搜索方向Pl,采用线搜索的方法确定搜索方向Pl上的最优步长α。
梯度计算公式为
gl=-2A(mref)TV-1[d-F(ml)]+2λLTLml
(11)
式(11)中:A为雅可比矩阵。
最优步长计算公式为
(12)
模型向量通过如下方式修正:
(13)
式(13)中:Pl为搜索方向;α为搜索步长。
式(13)中搜索方向通过如下方式修正:
(14)
式(14)中:Cl为预调节矩阵;βl利用Polak-Ribiere方法计算,即
(15)
由于NLCG反演算法已经是很成熟的方法,Rodi等[14]已针对其进行了详细的介绍,这里不做赘述。
2.2 深度学习反演
2.2.1 卷积神经网络结构
卷积神经网络(convolutional neural networks, CNN)是深度学习的代表算法之一,可实现卷积计算。目前,卷积神经网络已被广泛应用于人像识别、手势识别等领域[15]。卷积神经网络结构如图2所示。
卷积和池化层是卷积神经网络结构的核心组成部分。一般在卷积和池化层之后还需加入一层全连接层,卷积层可实现输入数据和卷积核的卷积操作。池化层的作用是降采样,可实现特征降维。卷积层和池化层实现了输入数据有效特征的提取,将经过特征提取后的有效特征输入全连接层,最终输出预测值。
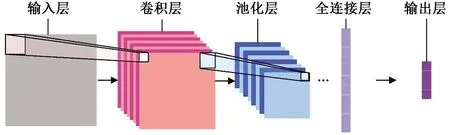
图2 卷积神经网络示意图Fig.2 The diagram of convolutional neural network
2.2.2 反演原理
基于卷积神经网络的航空大地电磁数据反演采用有监督的机器学习技术,即把观测点电磁响应数据作为训练数据,同时将相对应的地下电性结构作为标签。研究目标是把数据与标签之间的复杂关系利用卷积神经网络进行参数化,从而利用观测的电磁响应数据获得地下电性结构电阻率值。
用数学公式可以这样描述这个过程:给定一组电磁训练数据XTrain(倾子实部和虚部数据),地下电性结构数据YTrain。通过损失函数L去调整参数θ,使得输入数据集为XTrain,输出数据集为YTrain,最终获得参数化模型f(θ;XTrain)。神经网络参数更新表达式为
θ*=argminL[YTrain-f(θ;XTrain)]
(6)
假设该参数化的模型可近似表示电磁响应数据与地电结构标签之间的关系,只要训练和预测数据具有相同的分布且以相似的方式采样,其对应的地下电性结构便可由勘探数据Xpredict获得,该预测值的表达式为
Ypredict=f(θ*;Xpredict)
(7)
换句话说,只要训练数据和预测数据的勘探目标和环境相似,且数据采集和处理方式相同,就可以用训练好的神经网络模型来获得对应的地下电性结构。
3 算例
3.1 卷积神经网络反演算例
基于二维航空大地电磁法正演理论基础,采用有限单元法计算不同埋深的异常体地电模型倾子响应值,神经网络样本数据为倾子响应实虚部,标签为各异常体模型地下电性结构电阻率值。
3.1.1 样本数据集生成
首先创建一个初始异常体地电模型,如图3所示。该模型中异常体位于400 m埋深的地下介质中,大小为400 m×400 m,电阻率为10 Ω·m,地下介质电阻率为100 Ω·m。
然后将初始地电模型中异常体按照50 m间隔依次向右和向下移动,其构建过程如图4所示,共生成1 728组异常体地电模型。具体参数如下:所有地电模型的航空测线高度均位于地面以上100 m处,在y=-2 000~2 000 m的观测范围内,按照100 m间隔选择41个观测点采集磁场垂直分量。在y=-3 000 m处采集磁场水平分量。在1~1 000 Hz范围内,对数等间隔选择30个计算频率。针对这些地电模型采用有限单元法计算其倾子响应数据。

图3 异常体模型示意图Fig.3 The schematic diagram of anomalous body model
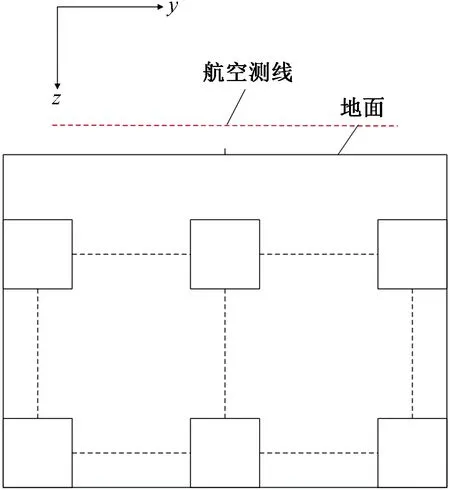
图4 不同位置异常体构建示意图Fig.4 The construction schematic diagram of anomalous bodies at different locations
最后针对各地电模型设置不同的地下电性结构电阻率值标签,在设置各地电模型标签时,在y=-2 000~2 000 m,z=0~2 000 m的观测范围,采用四边形网格按照50 m间隔剖分反演网格,最终各地电模型标签由3 200个反演网格构成,共生成1 728个地电模型标签。
3.1.2 数据预处理
针对3.1.1节中获取的1 728组样本数据,采用数据归一化方法进行归一化处理,数据的归一化操作可有效提升神经网络训练效率,避免梯度爆炸的产生。采用线性函数归一化方法实现样本数据的归一化,将样本集数据归一化到0.1~0.9,其表达公式为
(8)
式(8)中:X为原始数据;Xmin表示样本数据最小值;Xmax表示样本数据最大值。按照0.8∶0.1∶0.1的比例划分样本集为训练集、验证集和测试集。
3.1.3 卷积神经网络模型搭建
通过在卷积和池化层之后拼接一层全连接层,完成卷积神经网络模型的搭建。其中卷积层激活函数为relu,卷积核大小为32×3×3,池化层采用最大池化方法,在池化层后接一层flatten层实现一维数据的转化。采用adam优化算法和Dropout正则化技术对模型进行训练。最终建立的卷积神经网络模型参数如图5所示。
3.1.4 神经网络模型训练与测试
在进行卷积神经网络模型训练时,将神经网络的最大训练轮迭代次数设置为100。卷积神经网络训练和验证误差随迭代轮数变化趋势如图6所示,最终模型训练误差和验证误差分别为2.11×10-2、2.48×10-2。从测试集随机选择7组数据用于卷积神经网络模型测试,7组测试数据测试误差如图7所示,其测试误差平均值为2.44×10-2。
从测试集中随机选择两组样本进行卷积神经网络反演结果分析。表1展示了两组样本卷积神经网络反演模型测试结果。表1中不同样本对比数据来源于异常体的相同位置。从表1中可以看出,卷积神经网络反演电阻率与真实值更为接近,可有效表示真实电阻率。图8所示为不同位置和埋深的异常体卷积神经网络反演结果,其对应的模型真实背景电阻率均为100 Ω·m,异常体电阻率为10 Ω·m。由图8中可以看出,卷积神经网络输出的地电结构电阻率分布较为均匀,反演结果中异常体边界较清晰,异常体的位置和大小与真实异常体较接近。
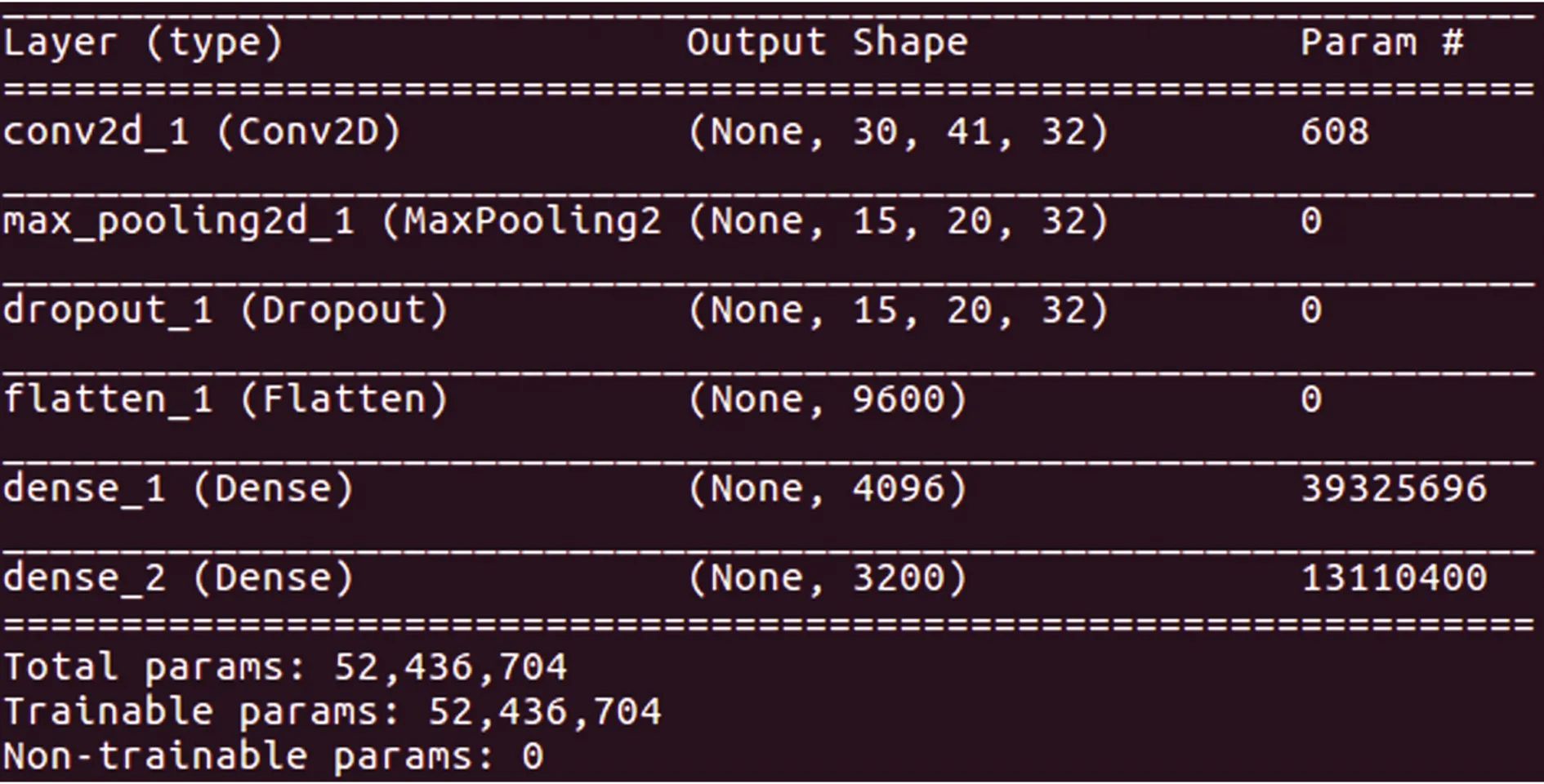
图5 卷积神经网络模型参数Fig.5 Parameters of convolution neural network model
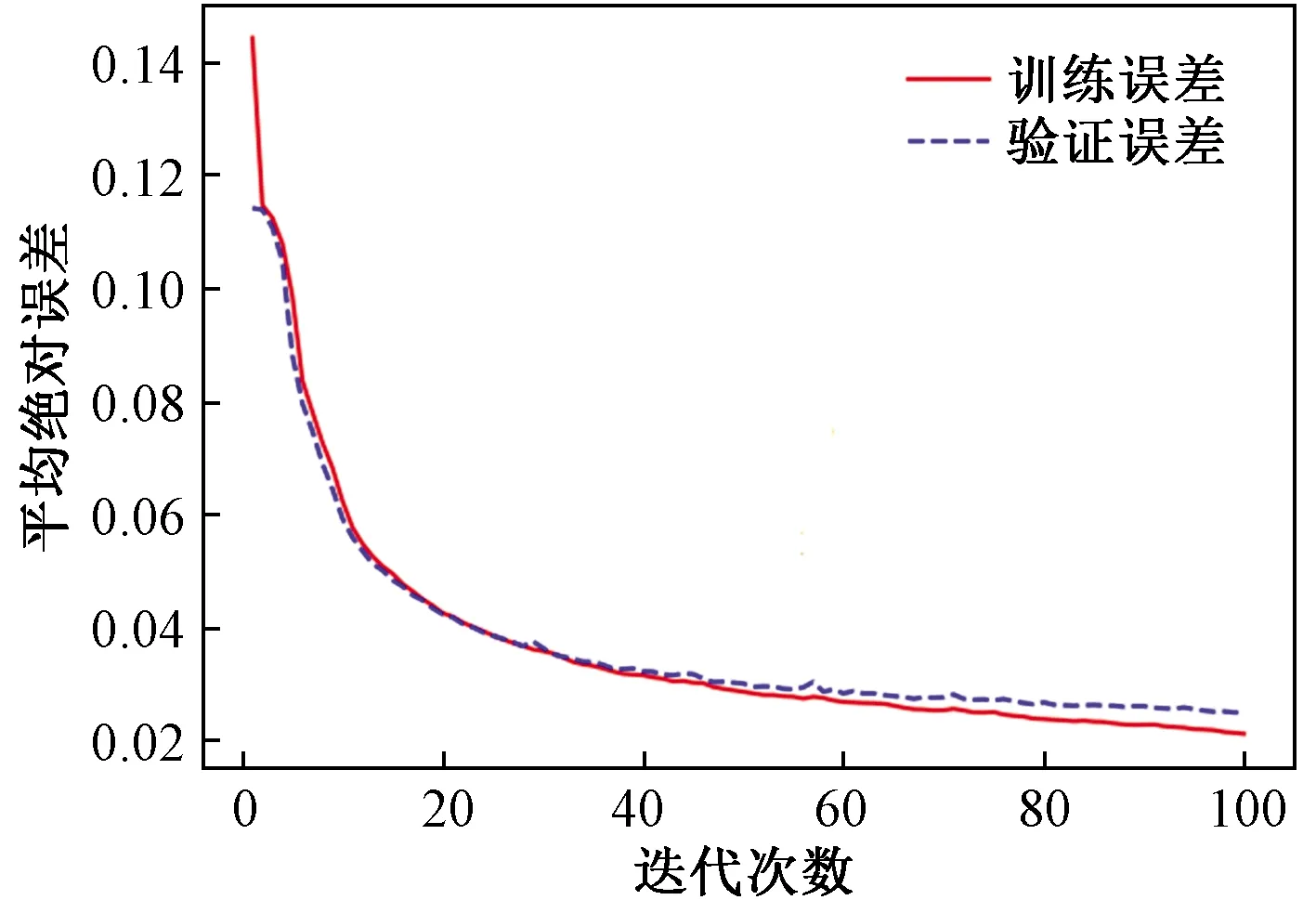
图6 卷积神经网络反演平均绝对误差Fig.6 Mean absolute error of inversion of convolution neural network

图7 7组测试数据测试误差Fig.7 Test error of seven test data

表1 卷积神经网络反演模型测试结果Table 1 Test result of convolution neural network inversion model

图8 卷积神经网络反演结果Fig.8 Inversion result of convolution neural network
3.2 传统电磁反演与深度学习反演
在反演阶段,首先针对一个550 m埋深的异常体模型,分别采用传统电磁反演方法和卷积神经网络反演方法进行反演测试。
采用传统电磁反演方法进行倾子数据反演时,首先,将反演初始模型背景电阻率设置为与真实的背景电阻率相同的100 Ω·m,其反演结果如图9所示,图中黑色虚线方框表示异常体的真实位置。从图9可以看出,反演结果对异常体的横向边界反演效果较好,但在垂向上存在明显偏差。接着,将反演初始模型背景电阻率设置为与真实背景电阻率不同的500 Ω·m时,其反演结果如图10所示,从图10中可以看出,当反演初始模型与真实模型电阻率相差较大时,单独的倾子数据反演结果不可靠。
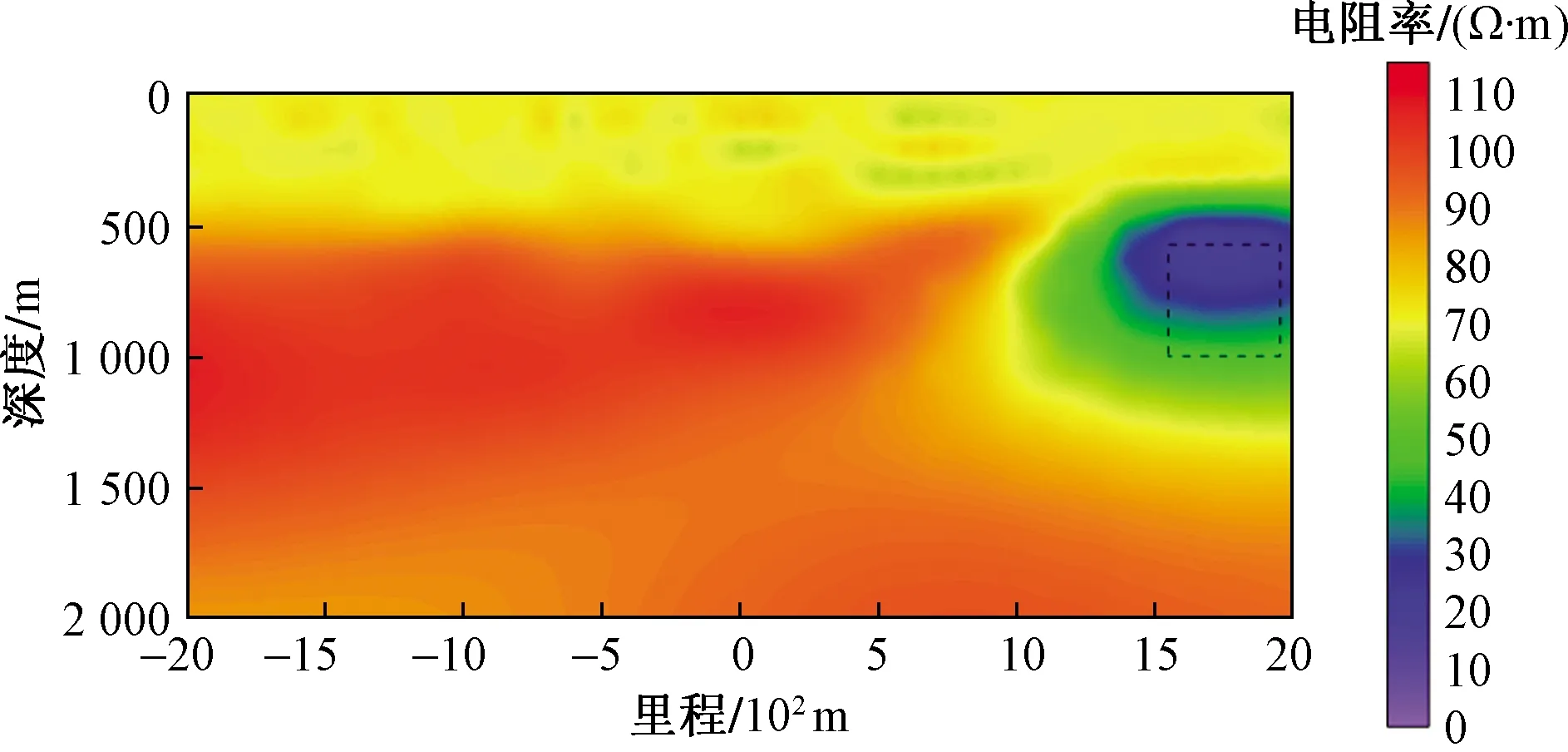
图9 异常体埋深550 m-传统电磁反演方法反演结果Fig.9 Inversion result of 550 m buried depth of anomalous body by traditional electromagnetic method
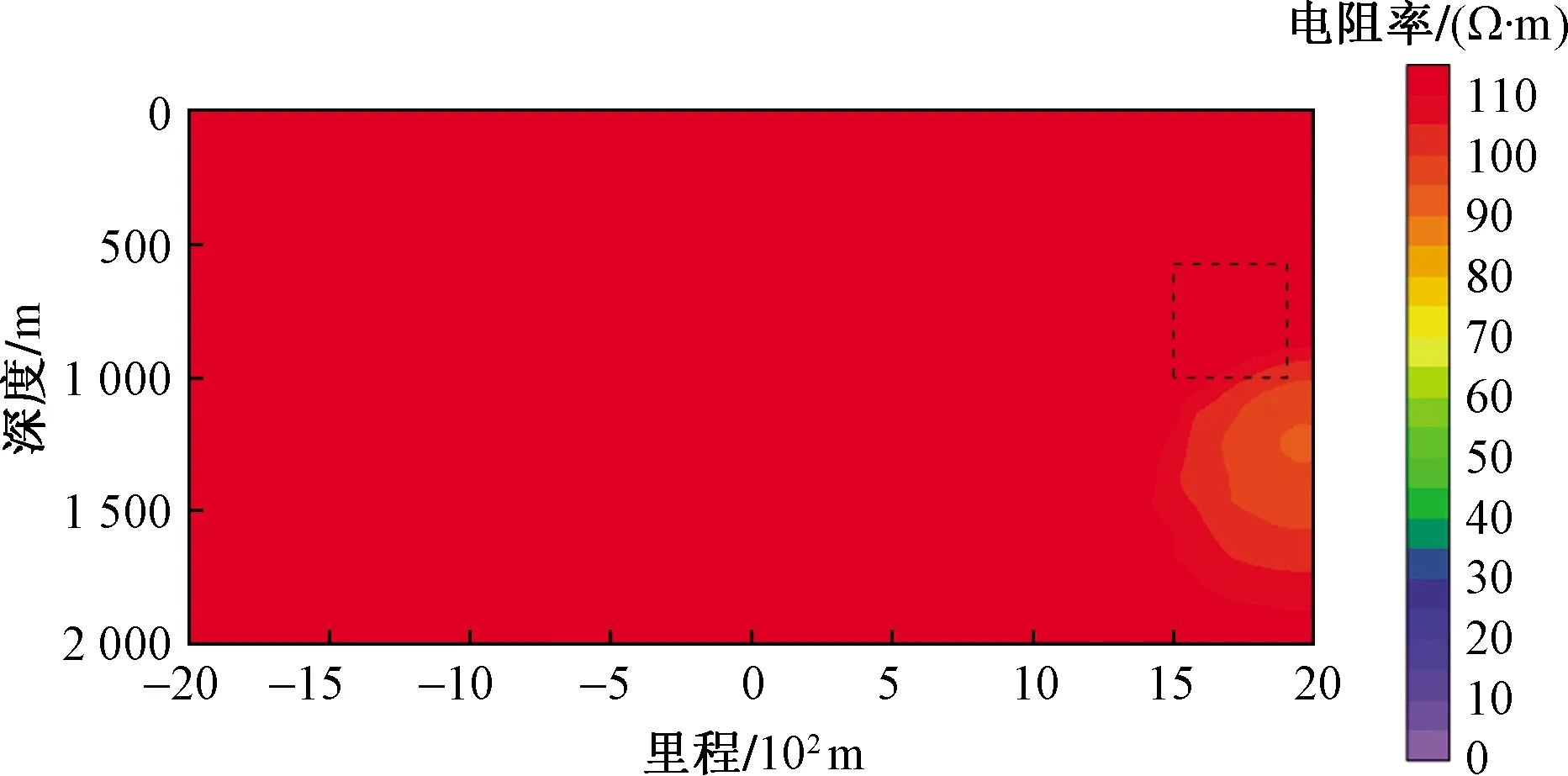
图10 初始背景电阻率500 Ω·m-传统电磁反演方法反演结果Fig.10 Inversion result by traditional electromagnetic method with initial background resistivity-500 Ω·m
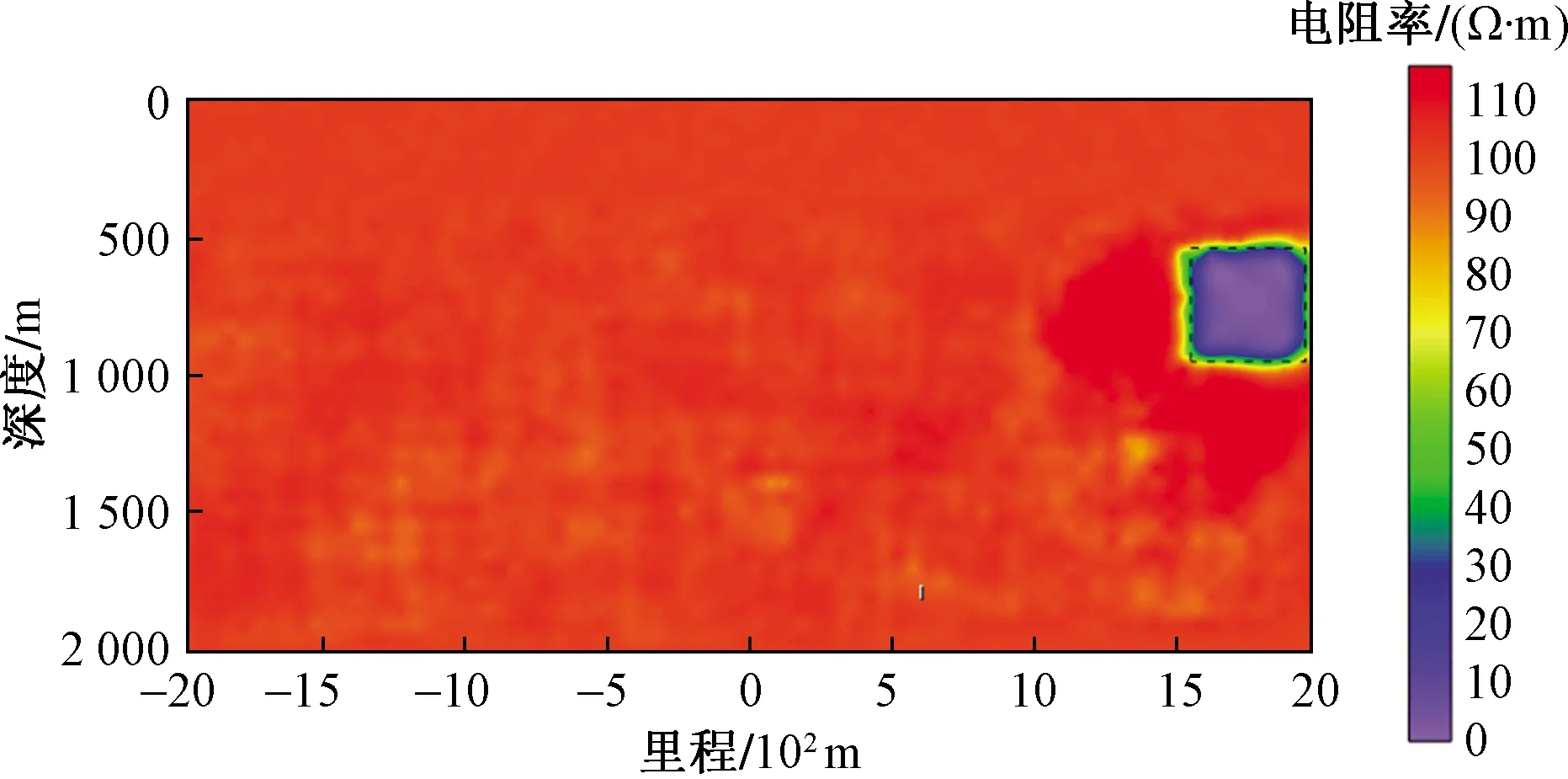
图11 550 m异常体埋深-卷积神经网络反演结果Fig.11 Inversion result of 550 m buried depth of anomalous body by convolution neural network
采用卷积神经网络进行倾子数据反演时,其反演结果如图11所示,图中黑色虚线方框表示异常体的真实位置。从图11中可以看出,反演结果中异常体的大小和位置与真实情况符合程度较高。对比图9和图11,可以得出结论:相比于传统电磁反演方法,采用卷积神经网络进行倾子数据反演时,反演结果更加准确、可靠。
接着针对一个750 m埋深的异常体模型,分别采用传统电磁反演和卷积神经网络反演方法进行倾子数据反演测试。采用传统电磁反演方法进行倾子数据反演时,将反演初始模型背景电阻率设置为与真实的背景电阻率相同的100 Ω·m,其反演结果如图12所示,图中黑色虚线方框表示异常体的真实位置。从图12中可以看出:当异常体埋深增加时,传统电磁反演方法反演结果中异常体的大小和位置已明显偏离真实位置,呈现出整体向下偏移趋势,反演结果已无法有效反映真实异常体的真实情况。
采用卷积神经网络进行倾子数据反演时,其反演结果如图13所示,从图13中可以看出:当异常体埋深增加时,卷积神经网络反演结果依然较好,反演结果中异常体大小和位置与真实情况非常接近。
最后,针对不同埋深异常体模型的传统电磁反演结果与卷积神经网络反演结果进行定量分析。表2展示了不同埋深异常体模型传统电磁反演方法反演结果与卷积神经网络反演结果。表2中不同样本对比数据来源于异常体的相同位置。从表2中可以看出,采用传统电磁反演方法进行倾子数据反演时,异常体反演电阻率较真实值偏大。相较于传统电磁反演方法,采用卷积神经网络进行倾子数据反演时,异常体反演电阻率与真实值偏差更小。
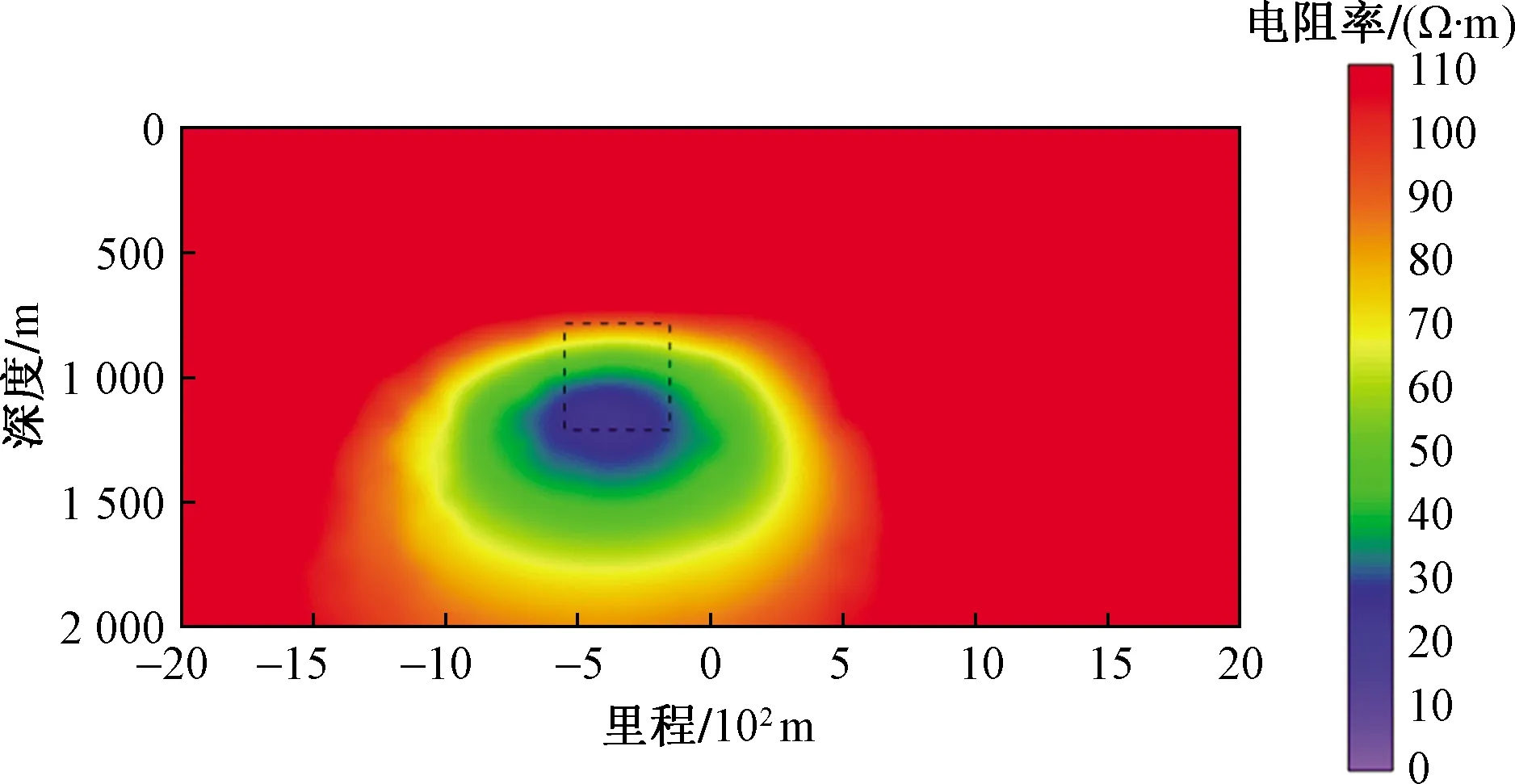
图12 750 m异常体埋深-传统电磁反演方法反演结果Fig.12 Inversion result of 750 m buried depth of anomalous body by traditional electromagnetic method
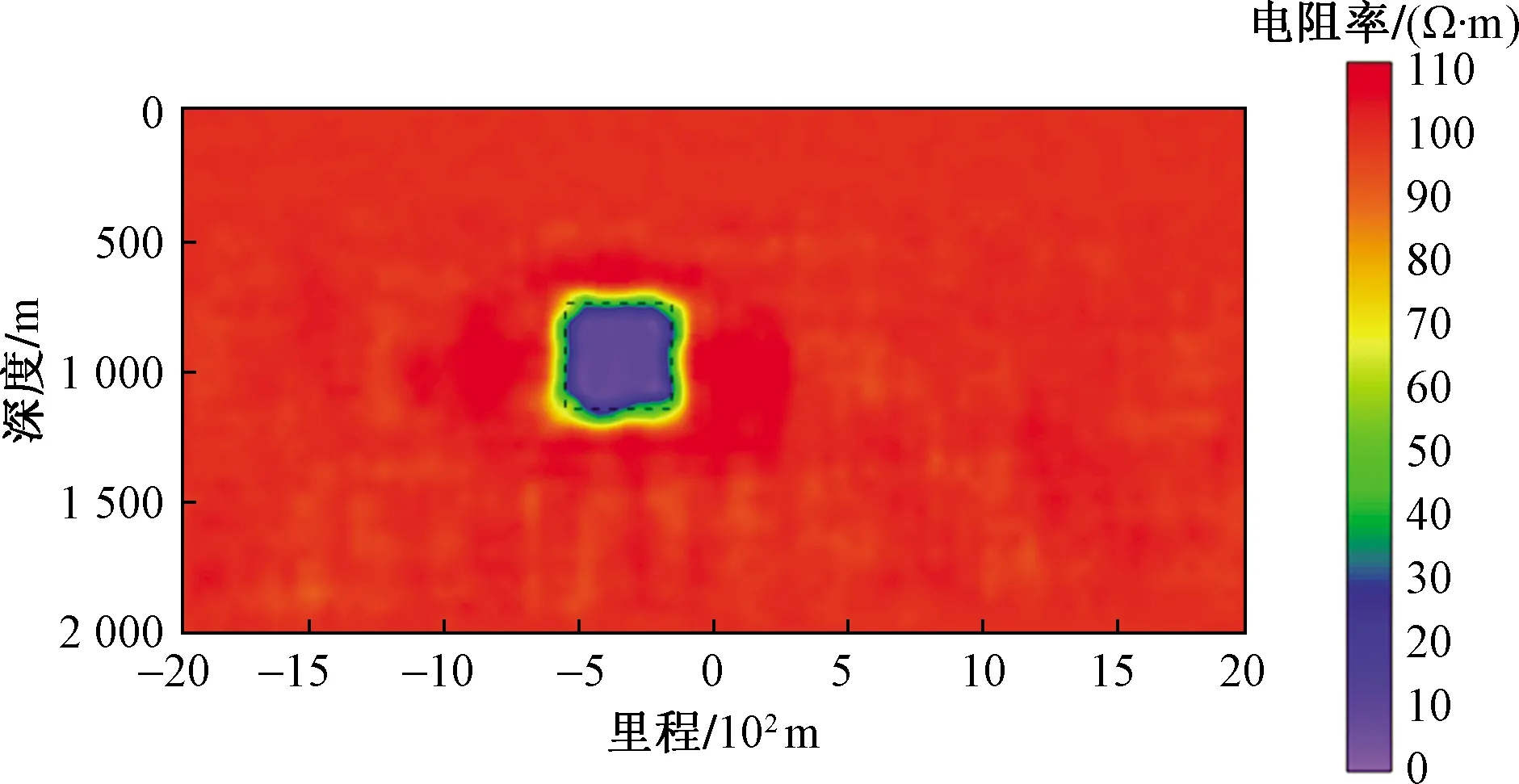
图13 750 m异常体埋深-卷积神经网络反演结果Fig.13 Inversion result of 750 m buried depth of anomalous body by convolution neural network
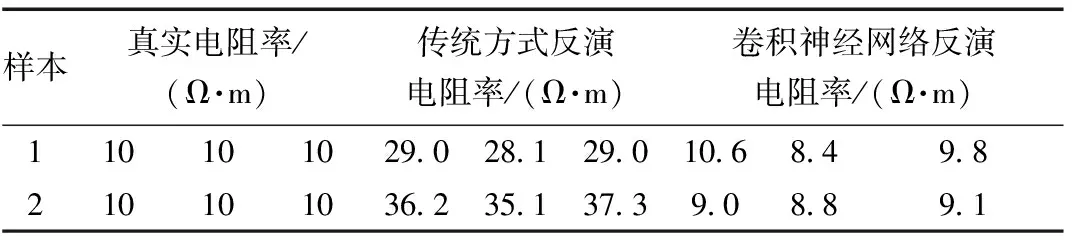
表2 传统电磁反演与卷积神经网络反演结果对比
综上所述,针对不同埋深的异常体模型,采用传统电磁反演方法进行倾子数据反演时,随着异常体埋深的增加,传统电磁方法反演结果已无法有效反映异常体的真实情况;采用卷积神经网络进行倾子数据反演时,反演速度快、准确度高,反演结果与真实情况更加接近。最终结果表明,采用卷积神经网络进行倾子数据反演,反演效果更好。
4 结论
首先从麦克斯韦方程组出发,推导了倾子响应计算公式,基于二维航空大地电磁法正演理论基础,针对地下介质中嵌入异常体的地电模型,采用有限元方法计算其倾子数据,并结合地下电阻率标签,构建了深度学习样本数据集。接着采用深度学习卷积神经网络实现了二维航空大地电磁倾子数据反演,针对不同埋深的异常体模型,分别分析了传统电磁反演和深度学习反演结果。最终结论总结如下。
(1)针对深度学习样本数据集,采用卷积神经网络进行二维航空电磁反演时,反演结果对异常体边界刻画较为清晰,异常体的位置和大小与真实异常体较符合,且反演电阻率值与真实值更为接近,可有效表示真实电阻率值。
(2)针对不同埋深的异常体模型,采用传统电磁反演方法进行反演时,反演结果对初始模型依赖度高,当反演初始模型与真实模型电阻率相差较大时,单独的倾子数据反演结果不可靠。随着异常体埋深的增加,传统电磁反演结果已无法有效反映异常体的真实情况;采用卷积神经网络进行倾子数据反演时,反演速度快、准确度高,反演结果与真实情况更加接近。相较于传统电磁反演方法,采用卷积神经网络方法进行倾子数据反演,反演效果更好。

