一种变系数动态剩余油饱和度方程的构建
张美玲, 张永超, 任雅楠, 樊家屹
(东北石油大学地球科学学院, 大庆 163318)
剩余油饱和度的定量评价是油藏开发的一项重要工作。由于取心法、测井法、油藏动态开发模拟法等多项技术都有各自的局限性,从地质、测井、生产动态等多方面资料入手,综合确定油层的剩余油饱和度已成为目前较为实际且有效的方法,尤其是利用密闭取心渗流资料来研究剩余油微观分布特征更有意义[1-2]。Andersen等[3]从岩心实验角度构建了关于孔隙度、渗透率及毛管压力的含水饱和度理论关系式;赖令彬等[4]通过岩心实验指出受岩层孔隙度和渗透率控制的毛细管直径存在差异的情况下,测量得到的相对渗透率与含水饱和度关系曲线并不相同。

油藏动态开发数据反映了实际生产中的水驱剩余油特征[9]。胡兴中等[10]以济阳坳陷第三系油层为研究对象,建立了含水率与含水饱和度的直线型方程,并指出公式中的系数与岩层的绝对渗透率及孔隙结构特征密切相关。相对渗透率测量数据是建立水驱特征与剩余油饱和度关系式的纽带,这种方法称为渗饱曲线法。Zhang[11]等通过实验数据研究了含水率与相对渗透率测量数据之间的关系,并尝试应用于实际生产中含水率的变化趋势,得到较吻合的结果。目前,常用的渗饱曲线法有指数法和因次法[12]。其中,指数法简单且未将束缚水和残余油饱和度考虑到公式中,适合以图版的方式给出剩余油饱和度[13-14];杨少春[15]采用系数c、n固定的因次法渗饱曲线方程确定剩余油饱和度是一种比较简单实用的方法。黄宏才等[16]利用孔隙度参数计算出束缚水饱和度及残余油饱和度,并采用固定系数的因次法渗饱公式,由文留油田某区块生产井的油水产出量推算出区块的剩余油饱和度。
以取心井相渗实验数据为基础,将因次法渗饱公式与水驱渗流公式结合,可以推导出依据含水率计算剩余油饱和度的公式。考虑到因次法公式的系数与岩层的孔渗特征有关系,建立了变系数因次法公式。变系数因次法的引入,可以有效考察不同孔渗条件的储层,在含水率变化量一致的情况下,剩余油饱和度的变化趋势。
1 方法原理
注入水在油层驱替过程中,由于孔隙和喉道分布的非均匀性,水并不能完全驱替出岩层中的油。在注入水端到采出油端的空间里,剩余油饱和度(仅考虑油水两相的情况,剩余油饱和度与含水饱和度的和等于1)分布是不连续的,特别是在采油端见到注入水之前,剩余油饱和度是逐渐增高的,表现为油水两相共同流动的区间。将注入水波及的位置定义为注入水前缘,该前缘到产油端之间,在原始含油饱和度为束缚水饱和度的条件下,为纯油流动区。前缘随时间推移由来水方向向产油方向移动,即两相流动区不断扩大,纯油区不断缩小,到产油端见水时,油层内就只剩下了两相流动区,油水相对渗透率曲线形态反映了油水分布状况[17]。这时,可依据巴克莱-莱弗里特研究平面一维水驱油问题解的思想来给出岩层油流量(qo)、水流量(qw)与水相对渗透率(krw)、油相对渗透率(kro)的关系。
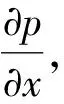
(1)
同一截面上不考虑毛细管压力,水、油两相的压力梯度相同,油的流量(qo)为
(2)
由式(1)、式(2)得出横截面上的含水率为
(3)
式(3)说明一个储集层到底是产油气,还是产水,或是油水同出,归根结底取决于油(气)水相对渗透率的大小。而油水相对渗透率曲线的油相和水相相对渗透率随含水饱和度的变化可以用因次关系表示[9],其表达式为
(4)
式(4)中:Sw为含水饱和度;Sor为水驱最终残余油饱和度;Swi为岩层束缚水饱和度;系数c、n受岩石孔隙结构、岩石润湿性、油水黏度比等多种因素的影响。式(4)说明给定岩心的油水相对渗透率与饱和度并不是一一对应关系。结合式(3)、式(4)可以推导出含水率fw、Sw、Swi、Sor之间的关系为
(5)
由式(5)可以得出,当一个岩层出水端含水率已知时,可以推测出该岩层的含水饱和度,进而推测出岩层的剩余油饱和度(1-Sw)。
2 系数c、n的确定
依据油水相对渗透率实验测定标准,优选大庆长垣6口密闭取心井17块岩样进行相渗实验测试。测试参数如表1所示。其中模拟油黏度及密度、注水黏度及密度与取心井所在区块的实际采出油、注入水一致。
按照式(4),系数c、n受岩石孔隙结构、岩石润湿性和油水黏度比等多种因素的影响。由于岩样取自一个开发区块的同一油藏,岩石润湿性及油水黏度比基本相当。在实际计算时,可以按照开发时间和区块统一测定给出。建立系数c、n与岩石孔隙结构参数Rc的关系式为
(6)
针对式(4)两边取自然对数得
(7)
令
(8)
(9)

表1 油水相对渗透率实验条件
按照式(8)、式(9)分别计算每个样点的x、y数据,由式(7)可知,针对每个样点可以拟合出y关于x的一元线性回归线,线的斜率为-n,截距为lnc。
表2给出了17个样点的孔隙度(φ)、渗透率(k)、束缚水饱和度(Swi)、残余油饱和度(Sor)、泥质含量(Vsh)、孔隙结构参数(Rc)等数据。表2中,最后两列为各样点拟合的lnc、n。从表2可以看出,n变化范围并不大,其中363号样的n=1.460 7,为最小值,520号样的n=1.787 8为最大值;lnc的变化范围较大,从1107号样品的-0.204 1变化到733号样品的1.701 1,即c的变化范围为0.815 38~5.479 97。
表2中,Rc反映了岩层孔隙喉道的大小,Rc越大,喉道半径也越大,孔渗条件也就越好[6],据此来分析各岩样的φ、k、Rc与n及lnc的关系。具有最小n的363号样对应的φ、k、Rc分别为30.6%、1 632.7 mD、7.306,而具有最大n的520号样对应的φ、k、Rc分别为24.6%、35.6 mD、1.203;具有最小lnc值的1107号样品对应的φ、k、Rc分别为24.8%、14.6 mD、0.767,具有最大lnc值的733号样品对应的φ、k、Rc分别为 32.2%、1 301.9 mD、6.358。
图1给出了Rc分别为7.306、3.075、0.767的3个样品(应岩样号分别为363号、909号、 1107号)的Sw-fw交会图及y-x交会图。这3个岩样分别表示孔渗条件好、中等、差3种情况的样品。从图1可以看出,y与x之间存在很好的相关性,孔渗条件不同,各样点呈现的Sw-fw及y-x关系并不相同。由此可见,n及lnc受岩层的孔隙空间大小及渗透性影响较大。

表2 不同样品相关实验参数及其各样点计算的lnc和n值
图2为Rc与lnc的关系图,反映了两者的正相关关系,关系式如式(10)所示,相关系数达到0.801,说明岩层的孔隙喉道越大,系数c值越大;图3为Rc与n关系图,两者为负相关关系,关系式如式(11)所示,相关系数达到0.859。
lnc=0.259 5Rc-0.233 5
(10)
n=-0.044Rc+1.822 1
(11)
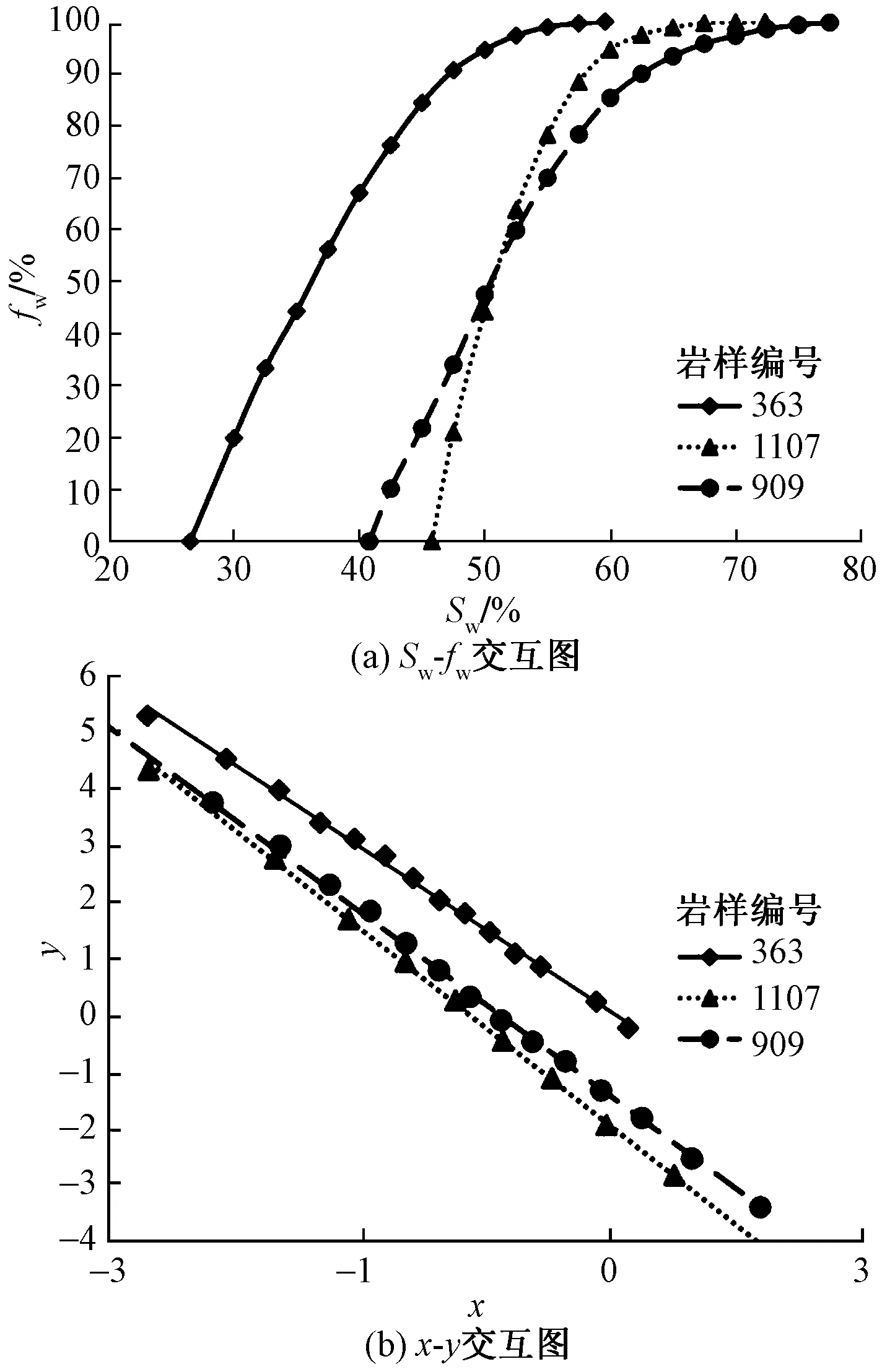
图1 典型样点Sw-fw交会图及y-x交会图Fig.1 Intersections of Sw-fw and y-x of typical samples

图2 各岩样的Rc与lnc的相关关系Fig.2 Correlation diagram of Rc and lnc of each rock sample
3 束缚水饱和度(Swi)与残余油饱和度(Sor)的计算
束缚水是指赋存在砂岩微细孔道中的残留滞水和靠表面分子力吸附在大孔道颗粒表面上的薄膜滞水,而残余油是指吸附在孔道内颗粒表面不流动的油[18]。研究区是砂泥岩沉积地层,砂岩中的细微孔道越多,渗透率越低,残留滞水越多;砂岩中泥质颗粒越多,泥质含量越高,泥质颗粒表面的吸附水越高。图4(a)、图4(b)给出了泥质含量(Vsh)及渗透率(k)分别与束缚水饱和度(Swi)的关系,并利用两者建立束缚水饱和度公式,如式(12)所示,相关系数为0.952。
Swi=0.447 7-0.034 7lnk+0.415 6Vsh
(12)
残余油饱和度(Sor)除了与岩层中石油的黏度有关系外,还应与岩层的孔隙度、渗透率有关系,同等黏度条件下,孔隙度越大、渗透率越大,残余油饱和度越低[9]。图5(a)、图5(b)给出了孔隙度(φ)及渗透率(k)分别与残余油饱和度(Sor)的关系,并利用两者建立残余油饱和度公式,如式(13)所示,相关系数为0.861。
Sor=0.447-0.386φ-0.018 48lnk
(13)
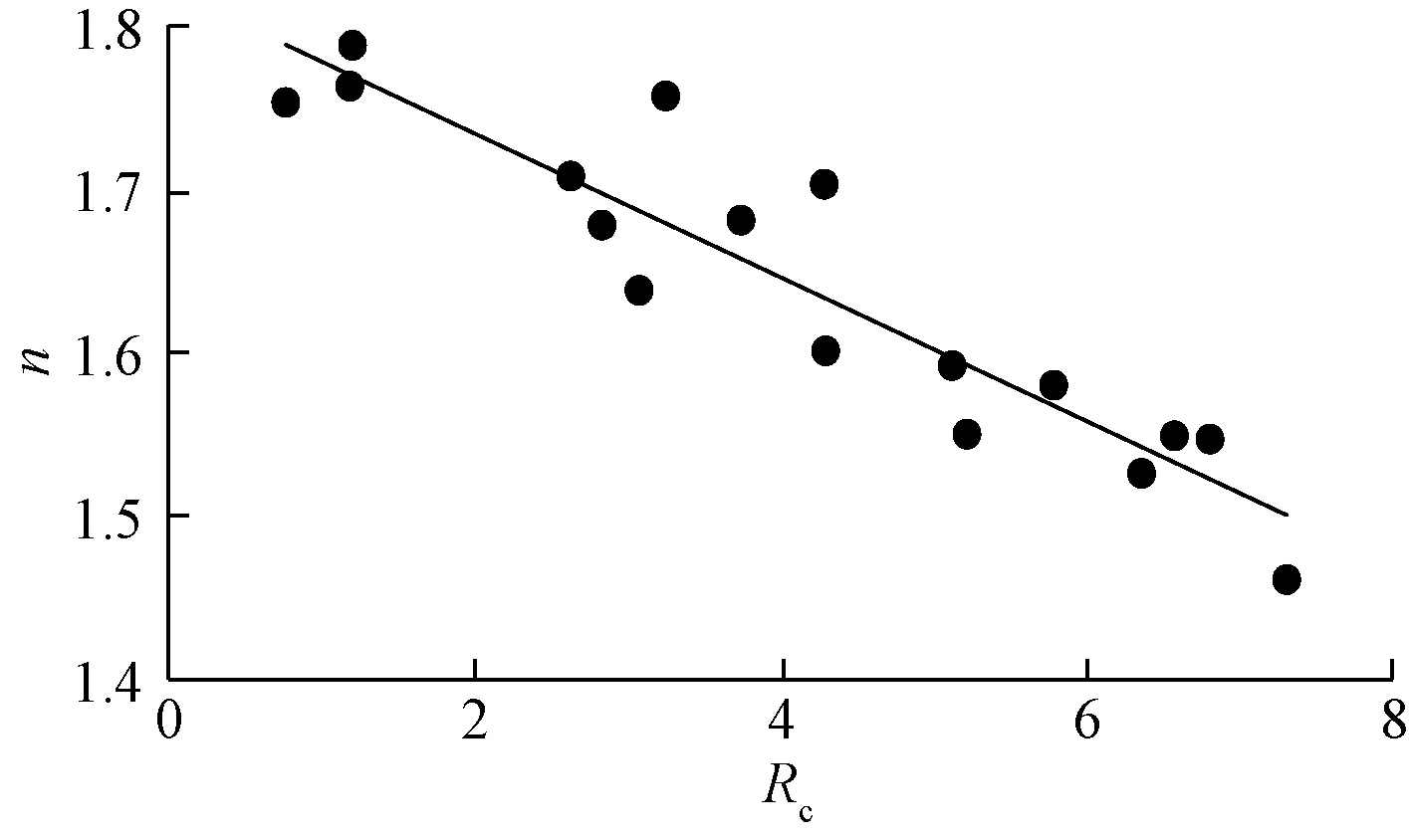
图3 各岩样的Rc与n的相关关系图Fig.3 Correlation diagram of Rc and n of each rock sample
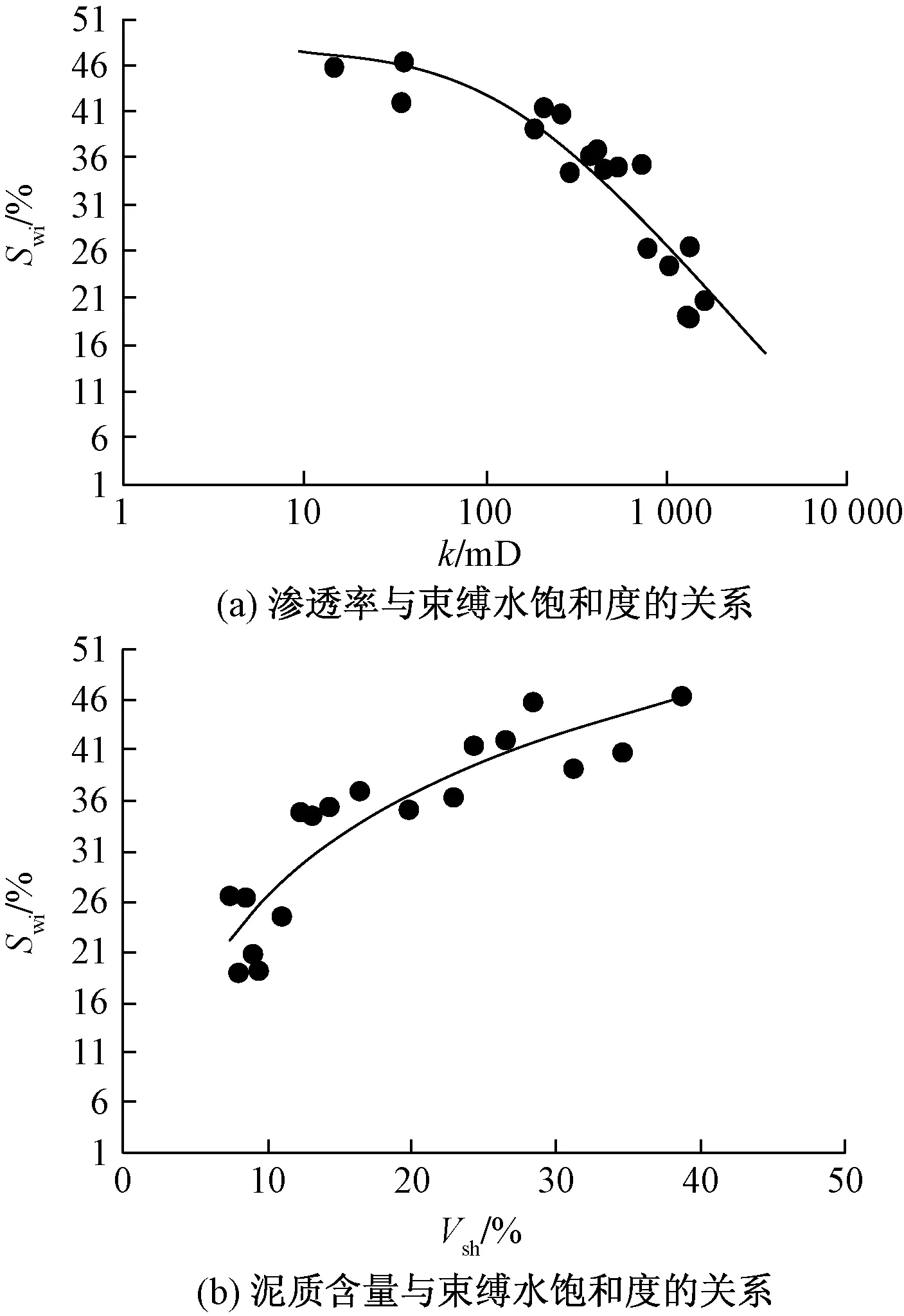
图4 渗透率和泥质含量与束缚水饱和度的关系Fig.4 Intersaction of permeability, shale content and bound water saturation

图5 孔隙度和渗透率与残余油饱和度的关系Fig.5 Intersection of porosity, permeability and residual oil saturation
4 方法应用
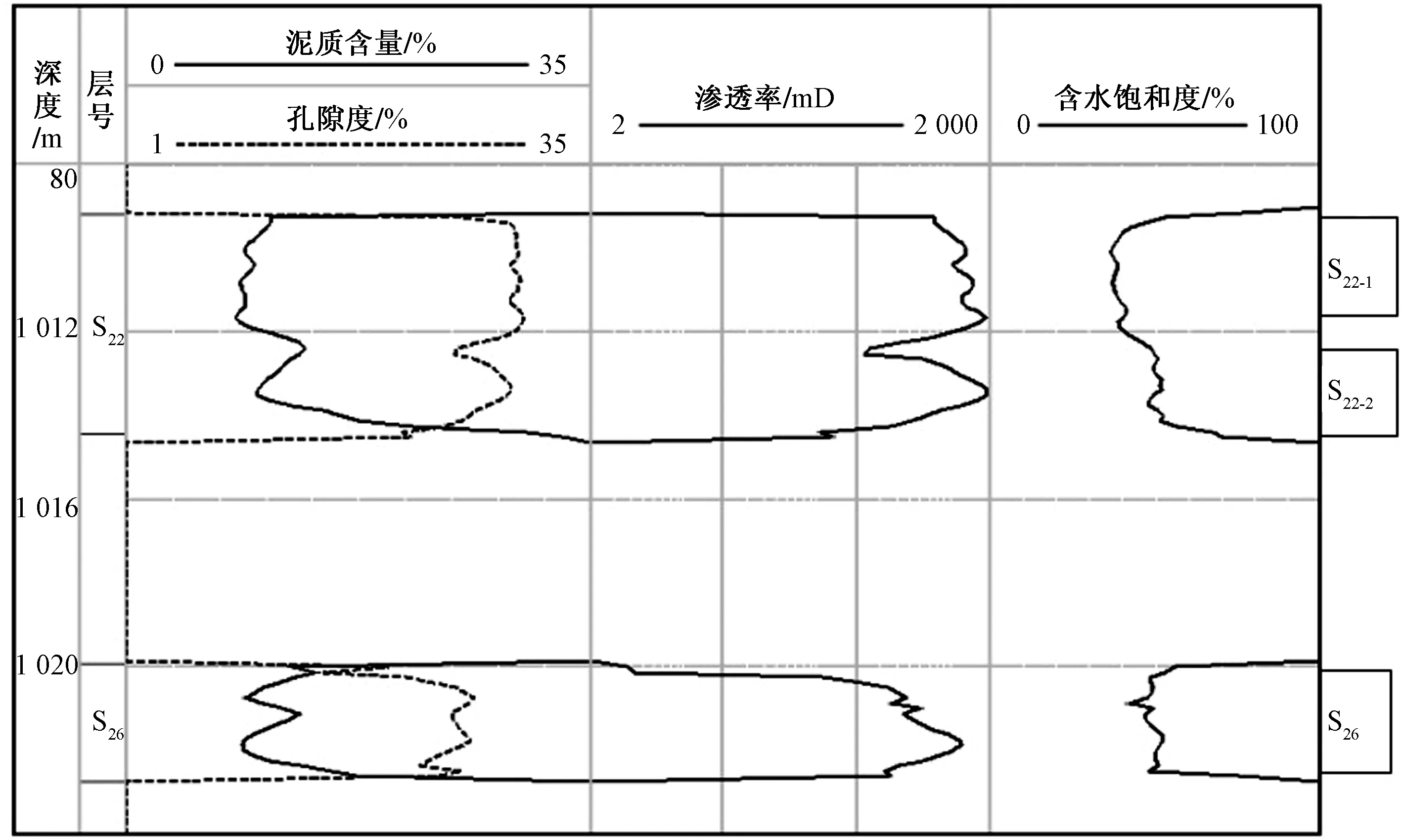
图6 加密井#1测井曲线计算相关参数结果Fig.6 Logging curves and related parameters calculated by logs of infill well #1
研究区新钻1口加密井中的S22、S26两个层分别进行了开采,含水率分别达到95%、50%。利用CIFLog软件由测井曲线分别计算了两个层的孔隙度(φ)、渗透率(k)、泥质含量(Vsh)和含水饱和度Sw0随深度变化的曲线,如图6所示。依据曲线(图6)分层原理[19],将S22层按上下两层(其中S22-1、S22-2)、S26按一层求平均分别给出孔隙度(φ)、渗透率(k)和泥质含量(Vsh)、含水饱和度(Sw0),如表3所示。
依据表3中的孔隙度(φ)、渗透率(k)和泥质含量Vsh,结合式(6)、式(12)、式(13)计算出Rc、Swi、Sor;再结合式(10)、式(11)计算出系数c和n。具体结果如表4所示。
将表3中分别为50%、95%的含水率代入式(5)计算出含水饱和度(Sw),其中计算出的S22-1、S22-2、S26的含水饱和度分别为68%、69%、42%,如表4所示。表3中,测井计算的含水饱和度分别为37.1%、50.1%、42.4%。分析发现,S26两者计算的饱和度一致,说明该层测试含水率50%是正常的开发效果,该层可以持续开采。而S22-1、S22-2由含水率计算的含水饱和度为68%、69%,明显高于测井计算的含水饱和度为37%、50%,说明当前生产的含水率95%并不反映地层中实际的剩余油状况,考虑到S22-2层内渗透率值在403~1 260 mD,非均质明显,存在高孔渗条带,怀疑该层出现低效循环“大孔道”[20],在此建议下,将S22-2高孔渗部分进行调剖封堵,含水率变为39%,将该值代入式(5)重新计算S22-1层Sw为39.1%,与测井结果吻合。
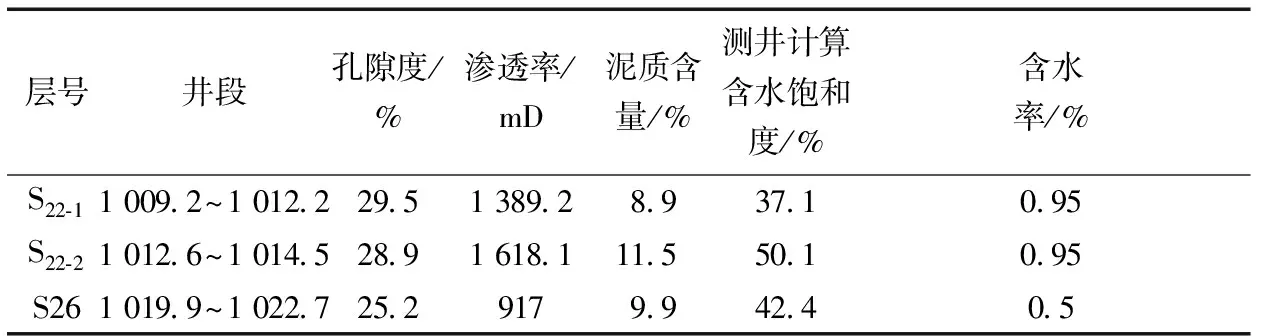
表3 加密井#1测井曲线计算参数的层平均值

表4 加密井#1开采层由测井曲线计算的相关参数Table 4 Related parameters calculated by logs of Infill well#1
5 结论
(1)因次法渗饱公式反映了相对渗透率、含水饱和度和含水率之间的有效关系,但并不是唯一关系,系数与岩样的孔渗特性密切相关。利用线性回归方法,优化确立因次法渗饱公式系数与岩样孔隙结构参数的关系式,吻合结果较好,进一步反映了岩层的孔渗条件对其开采程度的影响作用。
(2)因次法渗饱公式中的系数、束缚水饱和度以及残余油饱和度均可由孔隙度、渗透率、泥质含量来确定,而这3个参数可以由测井曲线计算得到。这样构建的变系数因次法渗饱公式符合“岩层孔渗性质不同、开采效果不同”的实际规律。
(3)尽管研究中没有考虑重力和毛细管力等因素,但研究成果仍可作为一种理想的背景情况来分析实际开采的动态信息。如某些油层开采初期含水率很高时,由含水率计算含水饱和度,当该饱和度远高于测井曲线计算的含水饱和度时,可以推断该油层中存在低效循环的“大孔道”,可采用封堵等方式来改善采油状况;当与测井曲线计算的含水饱和度基本相当时,说明该岩层的剩余油饱和度趋近于残余油状态,不必再采用增产措施。

