弹性变形对双座电动飞机模型气动特性的影响

佟胜喜， 李东辉， 赵庆贺， 高 峰， 范彦铭

(1.沈阳飞机设计研究所, 沈阳 110035； 2.辽宁通用航空研究院, 沈阳 110136; 3.沈阳航空航天大学航空宇航学院, 沈阳 110136)

为了降低航空运输带来的碳排放,采用新能源代替燃油的绿色航空成为航空界的研究热点之一。波音公司、空中客车公司,以及美国航空航天局(NASA)、德国航空航天研究院(DLR)等研究机构均开展了关于电动飞机技术的相关研究。中国在电动飞机领域也开展了相关的研发工作。中国商飞公司等单位共同发起研制了“灵雀H”氢燃料电混合动力飞机,中国航空研究院联合荷兰宇航院积极开展电动飞机领域的国际合作,辽宁通用航空研究院开展了系列电动飞机的研制工作,其中RX1E双座电动飞机、RX1E-A增程型双座电动飞机已经取得适航证并进入市场,目前正在进行四座电动飞机和水上飞机的研制工作。

电动飞机使用电能作为能量来源,主要有太阳能飞机、燃料电池飞机和蓄电池飞机等。现阶段电动飞机主要以锂离子电池组作为能源储备装置,受锂离子电池水平的限制,电动飞机较同等量级的燃油飞机的航时、航程等都偏低。为了增加电动飞机的航时,需要尽可能地提高飞机的巡航升阻比等气动指标[1-2]。因此,电动飞机与常规飞机相比,在气动布局方面需采用更大的展弦比。

飞机是一个弹性体,在气动载荷的作用下,机翼发生明显变形,当气动载荷为定常载荷时,结构的弹性变形是一个缓慢的过程,气动力和运动与时间无关,静气动弹性问题[3-7]就是研究飞行器在定常气动载荷作用下的变形问题。气动力和结构变形的相互耦合,气动弹性变形影响着飞行条件下的载荷重新分布、升力分布、阻力、操纵效率、飞机的配平以及静稳定性和操纵性等。

静气动弹性问题假设结构的弹性变形是一个十分缓慢的过程,如果机翼的结构设计不当,例如机翼的刚心与压力中心距离过大,当飞行器在较大的速压下飞行时,作用在机翼上的扭矩过大直至超过机翼的强度极限,导致机翼结构破坏。

当飞行速度比较低时,弹性变形的影响很小。随着飞行速度的增加,弹性变形的影响也越来越严大,甚至会使机翼变得不稳定,或使操纵面失效或反效。万志强等[8]通过使用基于偶极子网格法及线性气动力影响系数矩阵的线性静气动弹性分析方法对飞机进行了不同飞行高度、不同纵向过载下的静气动弹性响应特性分析。邓立东等[9]考虑了气动力的非线性问题,开展了飞机非线性飞行载荷计算方法研究。谢长川等[10]介绍了大展弦比大柔性飞机的气动弹性研究成果,着重提出了具有结构几何非线性的飞机的气动弹性和飞行动力学问题。严德等[11]开展了基于试验气动力的纵向机动飞行载荷分析,气动弹性对大展弦比机翼升力的展向分布的影响是飞机结构设计者考虑的一个重要因素。杨希明等[12]阐述了中外在气动弹性风洞试验开展的主要研究工作,指出了气动弹性风洞试验在飞行器研制中的重要意义。

辽宁通用航空研究院设计的RX1E双座电动飞机采用了较大的展弦比,其展弦比达到17.52,大展弦比飞机机翼的弹性变形相对较大,因此其受到气动力作用后的弹性变形也会更加明显。

现通过面元法[13-14]和计算流体力学/计算固体力学(computational fluid dynamics/computational structural dynamics,CFD/CSD)耦合方法得到锐翔电动飞机机翼在风洞试验条件下的弹性变形,并分析弹性变形对纵向气动特性的影响。

1 风洞试验模型

开展双座电动飞机风洞试验时,试验模型为 1∶6 全金属模型,翼展2.417 m,模型结构如图1所示。模型主要连接件使用合金钢,机身、机翼等部分使用铝合金加工。试验风速为70 m/s。对机翼部分单独建模并进行计算,使用CFD与机翼结构耦合计算机翼的变形,对比分析机翼弹性变形前后气动力变化和载荷变化情况。

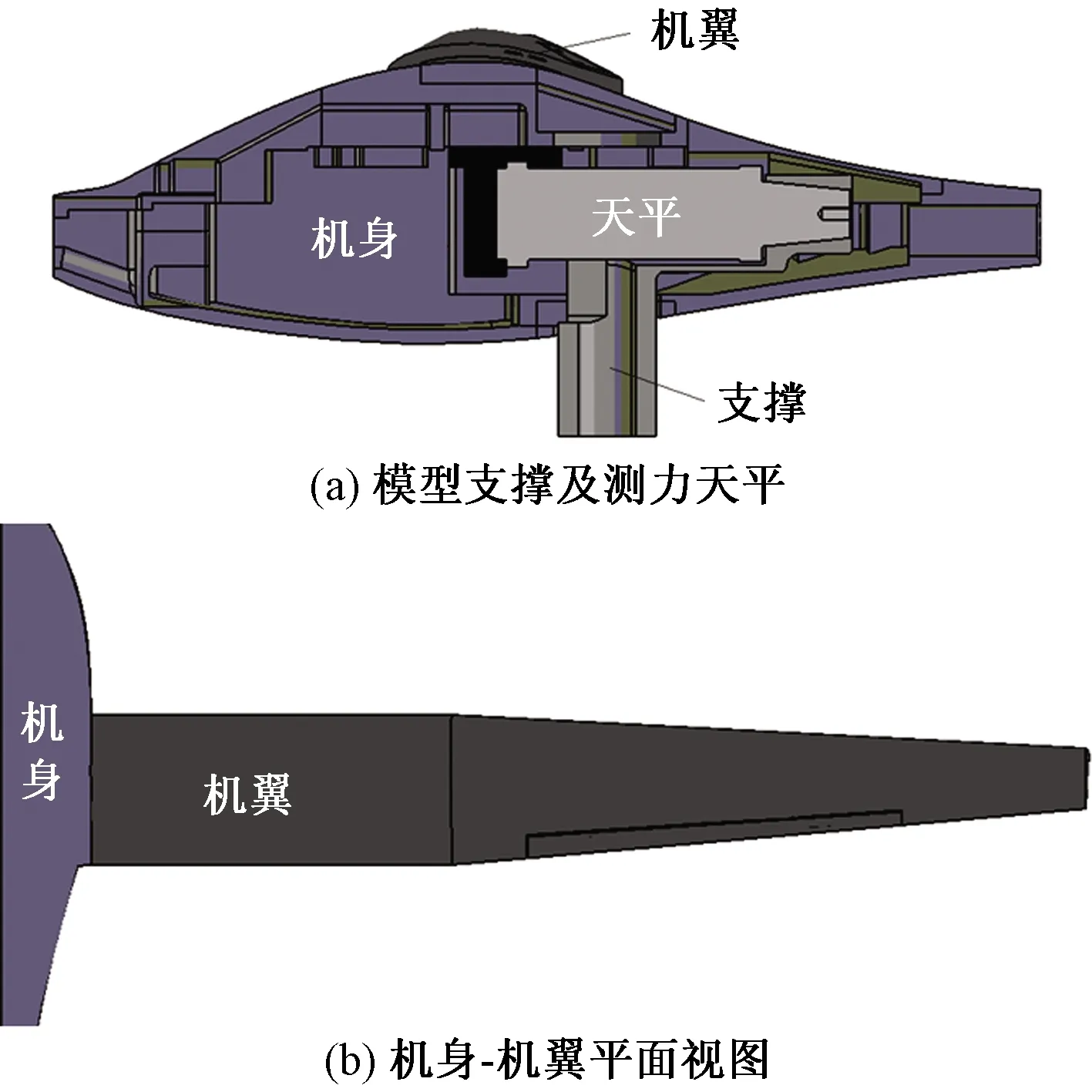
图1 机翼风洞试验模型Fig.1 The wind tunnel test model

2 电动飞机静气动弹性分析

2.1 面元法

相比于CFD,面元法可以快速高效地获得气动载荷,高阶面元法可实现对复杂外形飞行器三维气动力建模,相比于平板面元法能更好地模拟真实飞行器表面的流动情况。

首先采用Patran[15]划分机翼有限元网格,图2给出了机翼有限元网格以及采用获得的弹性变形。

为了缩短时域方法计算周期,减少存储量,结构计算采用简化的线性模态叠加方法,通过在物面施加近似边界条件,反复迭代求解得到结构体的实际变形。结构动力方程为

(1)

气动弹性分析需要对气动模型与结构模型进行耦合,使气动数据与结构数据相互传递。而气动弹性问题一般需要两个变换:①将结构模型的位移转换到气动模型的位移；②将气动模型的气动力转换成结构模型中的等效力。气动模型与结构模型耦合示意图如图3所示。

图2 机翼机构网格及位移变形Fig.2 Wing structure mesh and displacement deformation

图3 结构网格和气动网格数据传递Fig.3 Structural grid and aerodynamic grid data transfer

位移变换需要一个样条矩阵,公式为

uk=Gkgug

(2)

式(2)中：Gkg为样条矩阵；ug为结构模型中的位移；uk为气动模型中的位移。通过Gkg将结构模型中的位移转换成气动模型中的位移。

气动力等效通过虚功原理完成,空气动力Fk及作用在结构网格点上的等效值Fg再虚位移上做的功相同,公式为

(3)

式(3)中:δuk与δug分别表示气动力及结构点的虚位移。

将式(2)代入到式(3)中得到

(4)

由于虚位移的任意性,可得到气动力Fk与Fg的关系为

(5)

2.2 CFD/CSD流固耦合

为对比验证面元法获得的机翼弹性变形,采用了CFD/CSD流固耦合方法[16-20]进行计算。耦合迭代的过程中需要在气动模型和结构模型间进行数据交换,即将气动力插值到结构网格上,而把结构位移插值到气动网格上。另外,结构位移使得机翼物面变形,气动网格也要随之变形,因此,还需要在每一步迭代中实现网格变形。

采用基于非结构背景网格的动网格方法来实现CFD网格的快速更新。该方法结合了弹簧网格方法与代数背景网格方法的优点,变形能力强、计算效率高且鲁棒性好。

气动网格如图4所示,分别给出了机翼网格的整体视图及局部放大图。物面附近为六面体网格,过渡区域为金字塔网格,网格规模为5.32×106。

图4 机翼气动网格Fig.4 The wing grid partial view

采用有限体积法求解RANS方程,三维可压缩RANS方程可以写为

(6)

式(6)中：w是守恒变量；F、FV分别为无黏和黏性通量。

(7)

空间离散采用二阶中心格式,时间推进采用LUSGS隐式时间推进。湍流模型采用kω-SST两方程湍流模型。

2.3 风洞试验

在中国航空工业空气动力研究院FL-8风洞中进行全机缩比模型的风洞试验,图5给出了风洞试验模型在风洞中安装的照片。使用翼身组合体与光机身的试验结果差值得到机翼的气动力试验结果。试验中对支架干扰、洞壁干扰进行了修正。

图5 FL-8风洞中的试验模型Fig.5 Test model installed in FL-8 wind tunnel

3 弹性变形影响分析

静气动弹性问题研究飞行器弹性变形对定常气动载荷分布的影响以及由气动载荷所产生的静变形的稳定性。结构弹性变形将引起气动载荷的重新分布,气动载荷的重新分布不仅导致内部结构载荷和应力的重新分布,也会改变空气动力稳定性导数。

数值模拟的来流速度为70 m/s,质心位于根弦25%位置处,刚性轴为Z轴。计算时与风洞试验相同的条件进行计算。

3.1 弹性变形对机翼纵向气动力特性的影响

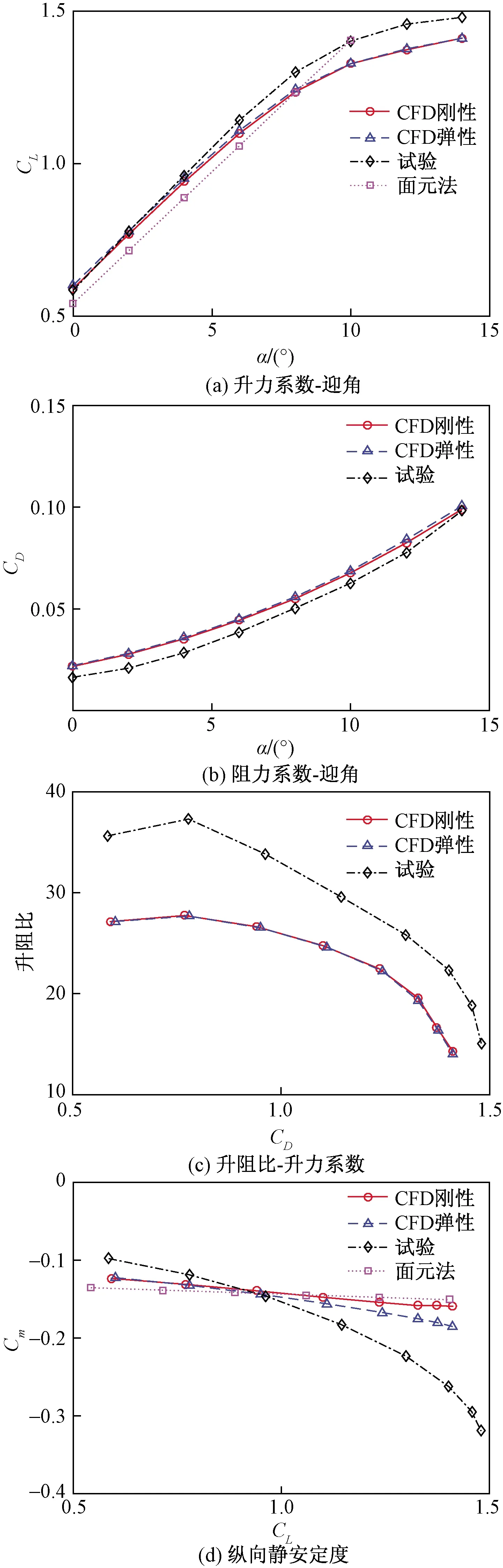
图6 机翼变形前后的气动特性Fig.6 Aerodynamic characteristics of wings before and after deformation

纵向气动力数据对比结果如表1所示,表中CL0为零迎角升力系数,CLα为升力线斜率,CD为阻力系数,α为迎角,Cm为俯仰力矩系数,dCm/dCL为俯仰力矩系数Cm对升力系数CL的导数,表征纵向静安定裕度。图6给出了面元法、CFD与风洞试验结果的对比曲线,参考点均位于25%平均气动弦长。通过数据和曲线可以看出,对于升力系数,CFD结果的升力线斜率略小于试验结果,面元法在线性段的值较试验结果整体约小0.04。受弹性变形影响,升力系数增加,阻力系数减小,相同迎角下的升阻比提高,相同升力系数下的升阻比基本没有变化。升阻比的CFD结果较试验偏小的原因主要是CFD的阻力系数偏大约0.005。

面元法与CFD计算的纵向静安定裕度远小于风洞试验结果。与刚性模型相比,弹性变形后的纵向静安定裕度显著提高,迎角2°时dCm/dCL值由刚性的-0.046变化至弹性的-0.061,且弹性模型的静安定裕度随升力系数的提高逐渐增大,到6°迎角时dCm/dCL≈ -0.08,刚性模型变化很小。弹性模型的静安定裕度随升力系数的提高逐渐增大的趋势与风洞试验结果相同。

表1 纵向气动力特性对比

3.2 机翼弹性变形对载荷的影响

根据CFD结果,分析弹性模型变形后弯矩、扭矩和剪切应力的变化情况。图7给出了不同迎角下的弯矩、扭矩及剪力,其中GM表示刚性模型,TM表示弹性模型。通过曲线可以看出,变形前后的弯矩及剪力变化不大,扭矩变化较为明显。

图7 机翼变形前后的气动载荷Fig.7 Aerodynamic loads before and after wing deformation

4 结论

为获得电动飞机的弹性变形,采用面元法及CFD/CSD耦合方法实现对机翼静气动弹性的数值模拟,并开展了静气动弹性风洞试验，结论如下。

(1)采用面元法获得的外载荷,在气动力的线性段与CFD/CSD趋势一致,升力系数约小0.05,计算结果表明该方法能满足工程实际中计算结果和计算高效的要求。

(2)受弹性变形影响,升力系数增加,阻力系数减小,相同升力系数下的升阻比基本没有变化。弹性变形对俯仰力矩系数影响显著,变形后的纵向静安定裕度显著提高,dCm/dCL由刚性的-0.046变化至弹性的-0.061,且弹性模型的静安定裕度随升力系数的提高逐渐增大,到6°迎角时dCm/dCL≈-0.08,刚性模型变化很小。大展弦比机翼在翼稍附近出现了明显的弹性变形。

(3)考虑弹性变形影响后的CFD/CSD纵向静安定性计算结果与风洞试验表现出了相同的随迎角增加趋势。

(4)机翼扭矩受弹性变形影响较大,弯矩和剪力几乎没有变化。