基于广义线性模型的混合属性数据聚类方法
朱永杰
(许昌学院信息化管理中心, 许昌 461099)
现代信息技术日新月异,社会各领域产生大量数据信息,可使用数据挖掘技术从海量数据中得到有效信息。数据聚类是一种使用频率较高的数据挖掘技术,在商品营销、图像处理、数据分析等领域应用较广[1]。实际应用中,可根据数据具体情况选择聚类方法。以混合属性数据为例,与单种属性数据不同,混合属性数据包含多种属性,如数值属性、符号属性、时间属性等[2]。由于属性种类较多,算法进行聚类过程中需通过转换方式将数据属性统一,属性转换过程复杂,容易降低算法聚类准确度。中外不少专家学者对混合属性数据聚类方法进行了研究,并取得了较好的研究成果。黄德才等[3]提出了混合属性数据流的二重k近邻聚类算法。采用二重k近邻和改进的维度距离形成数据的微聚类,根据均值的余弦模型以及动态标准化数据方法生成初始宏聚类,通过基于均值的余弦模型和先验聚类结果进行宏聚类优化,以实现混合属性数据的聚类,但是该方法存在聚类适应度较低的问题。Skabar[4]提出了一种基于随机漫步的混合属性数据聚类方法,该方法不需要任何显式的相似性或距离度量,就能够实现混合属性数据聚类,但是该方法存在迭代收敛速度较快的问题。现针对现有方法存在的问题,提出一种基于广义线性模型的混合属性数据聚类方法。引入低阶多元广义线性模型考虑数据属性时间特性,构建属性时间序列矩阵。用优化方法计算数据相异度、样本与聚类集间距离,当聚类结果趋于平稳时终止运算,输出聚类结果。通过此过程能够有效提高聚类适应度,提高聚类算法准确度,是提升混合属性数据聚类性能最为有效的途径。
1 混合属性数据聚类方法
1.1 低阶多元广义线性模型构建
定义yq(t)为混合数据属性的时间序列,混合数据属性聚类过程中,构建广义线性模型为
yq(t)=d(t)γq+
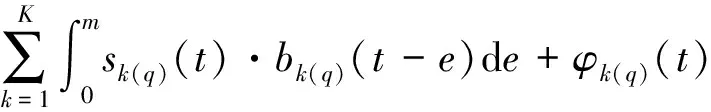
(1)
式(1)中:
φq为a维列向量;d(t)γq为数据属性混合导致的数据低频漂移;s(t)表示混合属性数据响应函数;K表示广义线性模型特征量指数;b(t-e)表示刺激函数。
采用广义线性模型完成混合数据聚类,可同时处理大量数据,提供更多的时间信息致使数据噪声干扰降低[5]。混合属性数据的响应函数存在差异,因此采用B-样条插值方法拟合混合数据的响应函数[6],过程为
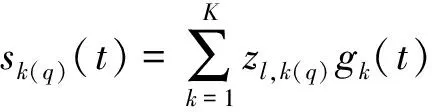
(2)
式(2)中:gk(t)和zl,k(q)分别表示B样条基函数与未知系数;sk(q)表示拟合混合数据的响应函数。
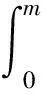

(3)
混合属性数据的特征信息全部体现在系数矩阵Qk,q中,采用最小二乘法求解即可。值得注意的是,广义线性模型参数多、混合属性数据信噪比低的特点导致最小二乘法求解结果变异概率高,将Qk,q变换成低阶矩阵相乘的方式解决该问题,具体过程如下:令Qk,q=Ek,qGk,q,Ek,q、Gk,q表示低阶矩阵,维数为L×P、P×D,P取值为2,变换后的形式体现了混合属性数据的时间特性[7]。混合属性数据聚类研究的是混合属性,所以模型的误入项应考虑到属性间的差异[8],据此扩展广义线性模型为低阶多元广义线性模型,即
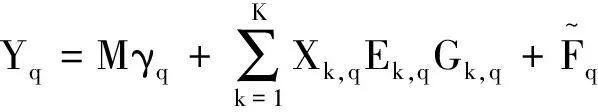
(4)
相比单一的广义线性模型而言,低阶多元广义线性模型存在以下优点:①可处理混合属性数据的聚类问题,使用领域扩大[9];②考虑了混合属性数据的时间特性,可处理大量混合属性信息,降低数据噪声,同时改善了聚类算法的聚类精度[10];③在低阶多元广义线性模型中,设置Ek,q矩阵为定值,对比Gk,q矩阵即完成混合属性数据响应函数的对比。
混合属性数据聚类过程中,应用到考虑时间特性属性的时间序列矩阵,可改善聚类算法精确度,详细聚类过程如下。
1.2 基于优化K-prototypes的混合属性数据聚类
由于基于K-prototypes的混合属性数据聚类方法[11]存在迭代收敛速度快、聚类精度低的问题,因此要对该方法进行优化。优化的K-prototypes混合属性数据聚类原理如下:首先,定义Xi(i=1,2,…,n)表示样本数据集,A1,A2,…,Ak表示聚类集,数据迭代过程中计算Xi与聚类集间的距离,将距离值最小的数据样本归类至聚类集内;其次,优化聚类及数值属性均值与分类属性值计数器,为获取聚类代价函数J(X,G)的最小值,迭代完成后更新分类属性模式。优化K-prototypes混合属性数据聚类算法考虑了属性的时间序列矩阵,可提高聚类精度,由此得到优化的相异度计算方法,样本分类属性值和聚类集内非未知样本属性值的不匹配概率和即为相异度[12],式(5)、式(6)分别为样本与聚类集间的距离计算方法,结合式(5)、式(6)获取分类属性距离计算结果。
μ(Xij,Aij)=1-|Alij|/|Al|Yq;μ∈[0,1]
(5)

(6)
式中:Al表示已有样本数量;|Alij|表示可分类样本Xi在分类Al内出现的频率;Yq为样本分类属性的时间序列矩阵;d(Xi,Al)为样本Xi与聚类集Al间的距离;Glj表示聚类集Al的数值属性均值。
定义以下参数:X={X1,X2,X3,…,X10},G={G1,G2,G3},G1=X7,G2=X2,G3=X5,A={A1,A2,A3},A1=[7,0,…,0],A2=[2,0,…,0],A3=[5,0,…,0]。K-prototypes算法聚类过程如图1所示,优化K-prototypes聚类算法如图2所示。

图1 K-prototypes聚类算法Fig.1 K-Prototypes clustering algorithm
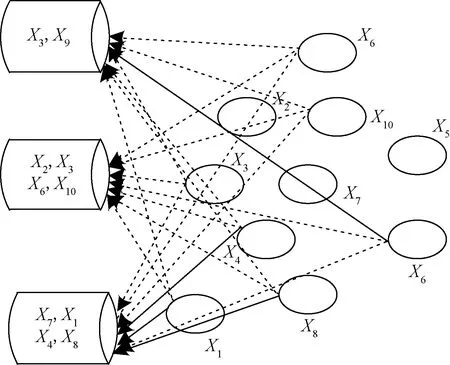
图2 优化K-prototypes聚类算法Fig.2 Optimized K-Prototypes clustering algorithm
分析图1可知,K-prototypes聚类算法迭代过程中,混合数据样本同聚类中心距离决定了数据样本的聚类[13]。图2信息表明,优化K-prototypes聚类算法在考虑样本同聚类中心距离基础上兼顾已知样本信息内容和属性的时间序列矩阵。详细分析图2中的样本X10,采用K-prototypes聚类算法得到以下形式:d(X10,G1)≥d(X10,G2)≥d(X10,G3),据此归类X10至A3。采用优化K-prototypes聚类算法获取上述3个样本到聚类中心的距离,根据距离最小原理归纳X10至A2。原因分析如下:根据图1和图2中样本节点排列情况可知,X10至X2距离等于X10至X5的距离,归纳X10至A2更合理是因为样本X3与X6存在A2内。总结优化K-prototypes算法聚类过程如下。
步骤1已知聚类数量为k,聚类集A的原始聚类中心样本是随机选择的原始节点G={G1,G2,…,Gk},那么A1={G1},…,Ak={Gk},同时定义η表示分类属性的权重值。
步骤2存在Xi(1≤i≤n,Xi≠Gj,j=1,2,…,k),与聚类集的距离表示为d(Xi,Al)。p表示聚类集元素计数器,设定p的初始值为1,归纳Xi至聚类集Amin中,Amin为距离最小的聚类集,若计数器值增加1,说明聚类运算了1次,用参数表示为Amin·p=i,p=p+1,新样本加入后,需再次计算聚类集Amin的数据属性均值,据此调整分类属性值计数器内容。
步骤3根据数据的混合属性差异获取聚类集原始聚类中心样本[14],原则为:数值型属性取聚类元素均值,分类型属性取聚类样本的分类属性中频繁出现的值。
步骤4各迭代目标函数值可依据目标函数公式(7)计算,即
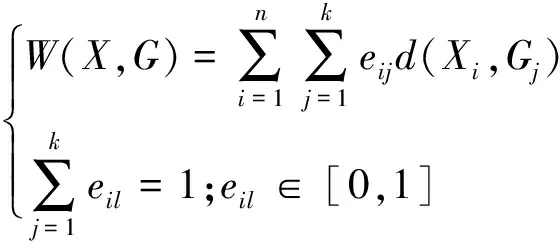
(7)
式(7)中:若eil为1,说明Al包含样本Xi;若eil为0,说明Al不包含样本Xi。
步骤5循环操作步骤2~步骤4,采用固定的迭代目标函数值,当聚类结果趋于平稳时终止运算[15],输出聚类结果。
采用广义线性模型与优化K-prototypes聚类算法结合的方法完成混合属性数据聚类[16],有效提升聚类算法处理混合属性数据的准确度。
2 实验分析
为验证本文方法对于混合属性数据的聚类优势,将文本数据作为混合属性聚类的样本数据,展开混合属性数据聚类分析测试。实验环境如下。①硬件环境:Inter(R) Corel(TM) Duo 2.00GHz CPU,内存为8 GB,使用Windows 10操作系统;②实验对比方法:K-prototypes数据聚类方法、二重K近邻聚类方法;③实验数据使用权威数据平台提供的语言词汇表,分为测试集A(包含5×102个混合属性数据)、测试集B(包含2×103个混合属性数据)与测试集C(包含5×103个混合属性数据),部分混合属性数据如表1所示。表1中,数据的混合属性包括分类属性与数值属性,分类属性为“渠道”“范畴”,数值属性为“时间”。
2.1 聚类方法性能对比
本次测试在数据量不同的测试集A、B、C中进行,不同方法混合属性数据聚类性能如表2所示。

表1 语言词汇
表2数据显示:在不同数据量的数据集聚类测试中,本文方法迭代时间在1 s左右、迭代次数约为21次,上下波动小,均优于其他两种聚类方法;本文方法进行混合属性数据聚类准确度均高于99.6%,不随数据量增加而降低,K-prototypes数据聚类方法、二重K近邻聚类方法聚类准确度随数据量增加而降低的趋势较明显;另外,3种方法最优解原始样本组数量均随测试集数据量的增加而增长,本文方法聚类后,得到最优解的原始样本组数量均高于其他两种方法。综上所述,本文方法进行混合属性数据聚类性能优于同类方法,之后详细分析本文聚类方法的具体优势。
2.2 平均目标函数值分析
采用本文方法在内的3种聚类方法进行混合属性数据聚类测试,3种方法聚类平均目标函数值与迭代次数关系如图3所示。
图3数据表明:3种聚类方法处理混合属性数据过程中,平均目标函数值均与迭代次数呈反比例关系;迭代次数一定时,本文方法的平均目标函数值最低,另外两种方法均高于本文方法,由于平均目标函数值越低,聚类精度越高,所以本文方法的聚类精度优于K-prototypes数据聚类方法、二重K近邻聚类方法;另外,由测试过程可知,迭代次数为20~30时,本文方法优化划分聚类集,迭代次数为30~42时,K-prototypes数据聚类方法优化划分聚类集,迭代次数为38~48时,二重K近邻聚类方法优化划分聚类集,相比之下,本文方法仅使用较少的迭代次数即可优化划分混合属性数据的聚类集,说明本文方法效率较高。
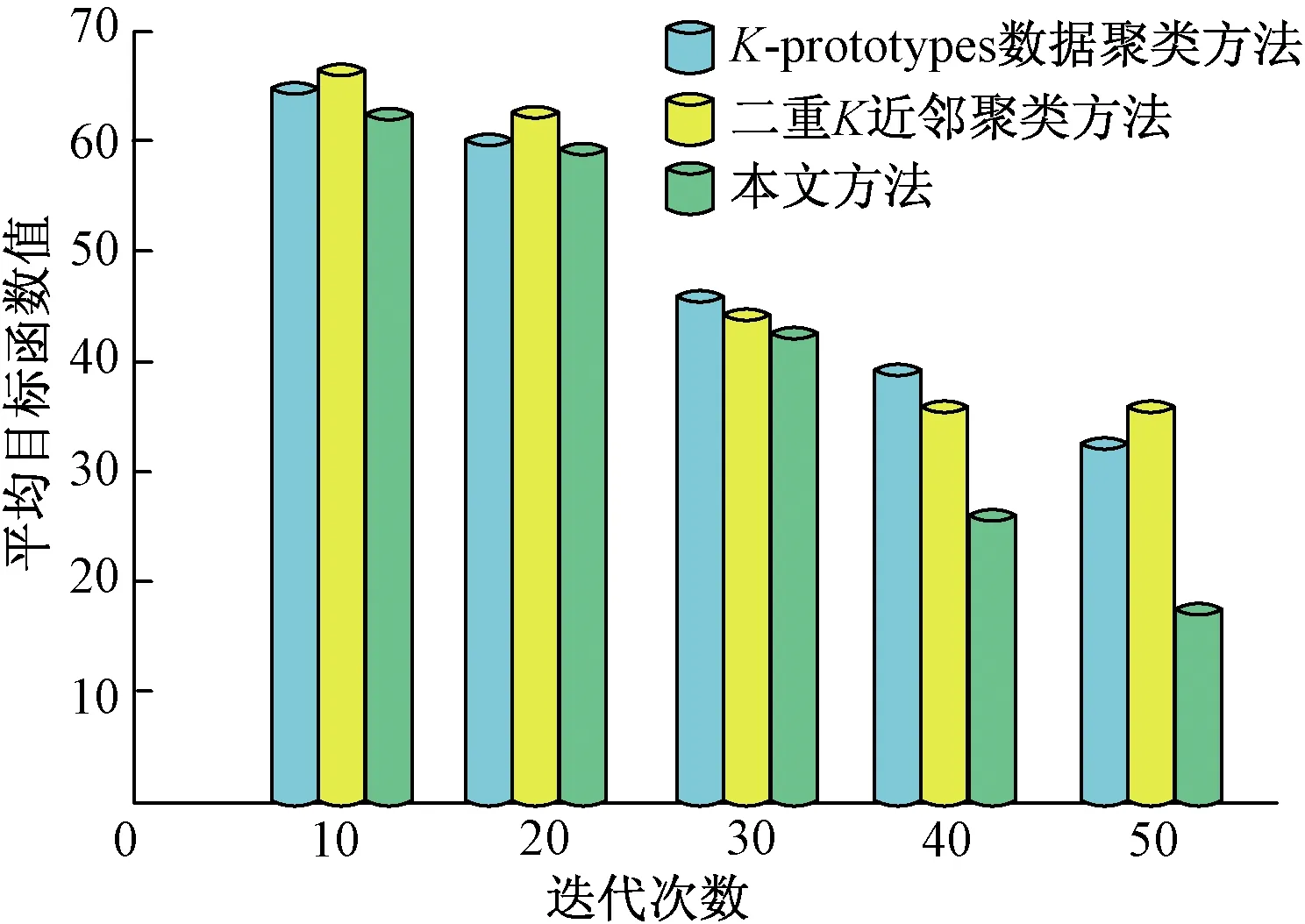
图3 平均目标函数值与迭代次数关系Fig.3 Relationship between average objective function value and iteration times
由于本文方法对混合属性数据进行聚类过程中,考虑到聚类集中的已有样本数据,所以减少了迭代分析次数,提高数据聚类效率,这也是本文方法相对同类型K-prototypes数据聚类方法的优化与改进之处。
2.3 原始样本数量与迭代次数关系分析
迭代次数影响混合属性数据聚类效果,2.2节实验对迭代次数与聚类方法的平均目标函数值关系进行分析,为全面掌握迭代次数对聚类效果的影响与干扰,本次实验测试聚类方法迭代次数与最优解原始样本组数量的关系,测试结果如图4所示。
分析图4可知,迭代次数一定时,本文方法得到最优解样本数量大于K-prototypes数据聚类方法、二重K近邻聚类方法,以迭代次数20次为例,本文方法有55个原始样本组达到最优解,K-prototypes数据聚类方法有33个原始样本组达到最优解,二重K近邻聚类方法有23个原始样本组达到最优解;另外,本文方法聚类迭代30~50次时最优解样本数量趋于稳定,另外两种方法没有趋于稳定的迹象,证明本文方法可靠性较强。上述数据表明,本文方法进行混合属性数据聚类过程中,聚类性能优于另外两种方法,且迭代稳定性、可靠性强。

表2 不同方法聚类性能对比结果
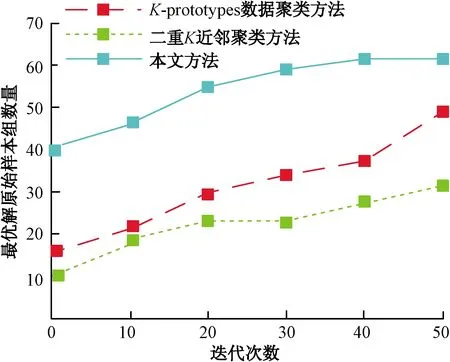
图4 迭代次数与初始样本组数量的关系Fig.4 The relationship between the number of iterations and the number of initial sample groups
2.4 适应度分析
聚类适应度影响聚类方法性能,因此,对3种混合属性数据聚类方法的适应度进行测试,测试结果如图5所示。
从图5能够看出,3种聚类方法适应度随时间的进化过程,本文方法适应度值在0.88~0.94,处于稳定发展状态,K-prototypes数据聚类方法适应度先增加再降低,最高适应度值为0.68,二重K近邻聚类方法呈由高至低的状态,实验结束时适应度值仅为0.3。
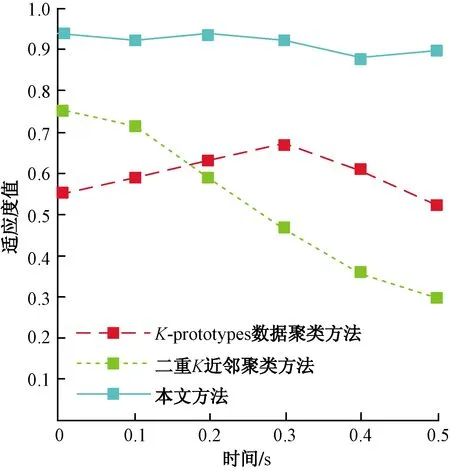
图5 适应度变化曲线Fig.5 Fitness curve
总体看来,本文方法适应度值最高,适应度最强,增强了混合属性数据聚类的性能。
3 结论
提出一种基于广义线性模型的混合属性数据聚类方法,实验证明本文方法解决混合属性数据聚类问题性能较优,相比同类方法具有优势。
总结本文提出的基于广义线性模型的混合属性数据聚类方法优点如下:①构建低阶多元广义线性模型,考虑了混合属性样本数据的时间特性,得到混合属性时间序列矩阵,提升聚类算法准确度;②迭代聚类过程中,参考混合属性数据样本同原型的差异,样本与聚类集间的距离计算采用更新的相异度公式与距离公式,得到的距离结果更加精准,有效提高聚类准确度。

